考虑预应力损失的锚索加固条件下边坡长期稳定性分析

邓东平，李 亮

(中南大学 土木工程学院， 长沙 410075)



考虑预应力损失的锚索加固条件下边坡长期稳定性分析

邓东平，李 亮

(中南大学 土木工程学院， 长沙 410075)

实际工程中，岩土体存在的蠕变性质使得加固于边坡上的锚索其预应力随时间而发生损失，从而引发边坡长期稳定性问题。为了正确评估预应力锚索加固边坡的长期稳定性，基于滑动面底面应力假设，并融入锚索预应力损失模型，建立一种新的预应力锚索加固条件下边坡长期稳定性极限平衡计算方法，以此来求出预应力锚索加固条件下不同时期边坡安全系数大小，进而反映边坡稳定状况的动态变化。通过工程实例分析，验证了该方法的可行性，并证实了锚索预应力损失可使得边坡长期稳定性变差。同时，经锚索预应力损失对边坡长期稳定性影响的多参数研究，表明提高锚索的初始预应力值是改善边坡长期稳定性的一种可靠有效途径。

边坡；长期稳定性；锚索加固；预应力损失；安全系数

1 研究背景

预应力锚索[1-5]具有施工速度快的特点，其对边坡的加固作用主要是通过改善岩土体的强度性质，并减小岩土体的变形以使岩土体达到要求的安全度[6-9]，从而提高边坡的整体稳定性，故其对边坡加固效果显著，因此，它被广泛应用于边坡治理工程中[10- 12]，且已取得了良好的经济效益。如赵晓彦[13]将预应力锚索加固应用于类土质边坡；吴茂明等[14]详细介绍了预应力锚索在路堑边坡和复杂地质条件下的应用；郑筱彦[15]将预应力锚索应用于李家峡水电站岩质高边坡。

以往针对锚索加固条件下的边坡稳定性分析，大多数研究成果主要集中于锚索对边坡的加固效应，或锚索设计参数对边坡稳定性的影响。如张发明等[16]对锚固间距、锚固角、锚索荷载及内锚段长度等参数进行优化分析；晏鄂川等[17]采用正交试验设计法分析锚固参数的组合方案，研究锚固参数对边坡稳定性的影响；许明等[18]针对典型岩质边坡，通过数值模拟试验，探讨群锚失效后边坡稳定性的劣化过程和失稳形态等问题。然而，锚索的预应力是通过锚具最终作用于边坡岩土体上，边坡岩土体实际存在一定的黏性，故在预应力作用下岩土体的形变不会瞬时完成，从而导致锚索的预应力存在长期损失[19-21]，因此，分析锚索加固条件下的边坡长期稳定性具有重要的工程应用价值。

本文基于滑动面底面上的应力假设，并将锚索预应力当成作用于滑动面上的加固力，从而建立一种新的锚索加固条件下边坡稳定性极限平衡计算方法。同时，根据前人研究成果，考虑锚索预应力的长期损失，将边坡岩土体蠕变和锚索预应力损失耦合模型与边坡稳定性计算公式相结合，以此分析锚索加固条件下边坡的长期稳定性问题。通过工程算例分析，验证了本文方法的可行性，并研究锚索预应力损失模型中各参数对边坡长期稳定性的影响。

2 锚索加固条件下边坡稳定性计算方法

2.1 滑动底面应力假设

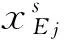
在以往研究中，通常假定锚索Ej上施加的预应力Qj作用于滑动面，并以此来分析其对边坡的加固效果。如图1(b)所示，在滑动体内任取宽度为dx的竖直微条分abcd。通过对微条分abcd进行受力分析，可知一般情况下作用在其上的力有：重力Wdx、锚索预应力Qj、滑动底面上的法向力σdx/cosα和剪切力τdx/cosα，其中，σ和τ分别为滑动底面上的正应力和剪应力，α为滑动面切线在水平方向上的倾角。

图1 锚索加固条件下边坡稳定性分析模型Fig.1 Model of analyzing the stability of slope reinforced with anchorage cable

当不考虑条间作用力的影响时，微条分abcd内各力在x和y轴方向上的力平衡条件分别为：

(1)

(2)

式中：s′为滑动面方程对x的一阶导数且s′=tanα；σ0和τ0分别为不考虑条间作用力影响时滑动底面上的正应力和剪应力。

求解式(1)和式(2)，可得σ0为

(3)

由于σ0未考虑条间作用力的影响，故其与实际的正应力存在着一定的差异，可采用式(4)对其进行修正以使得滑动底面上的正应力σ更接近于真实值。

(4)

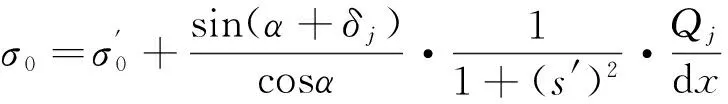
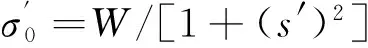
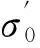
假设边坡滑动为剪切破坏，并服从摩尔-库伦强度准则，则可得滑动底面上正应力与剪应力的关系为

(5)

式中：Fs为边坡安全系数；c为土体黏聚力；φ为土体内摩擦角。

将式(4)代入式(5)中，并采用式(6)对滑动底面上的剪应力进行假设，即

(6)

式中λ2和λ3均为计算变量。

由整个滑动体内各力在x和y轴方向上的力平衡条件及绕某点(xc，yc)的力矩平衡条件，可得：

(7)

(8)

(9)

将式(7)、式(8)代入式(9)，并将式(9)简化为

(10)

将式(4)、式(6)代入式(7)、式(8)、式(10)中，可得关于计算变量λ1，λ2，λ3的一元三次方程组，即

(11)

式中aij和bi为计算参数，其计算式见表1。

2.2 安全系数计算

当边坡滑动为剪切破坏时，边坡的安全系数Fs可表示为沿滑动面上总的抗滑力和下滑力之比，即

。 (12)

3 锚索预应力损失模型

施加在锚索上的预应力一般通过锚具最终作用在边坡岩土体上，而实际工程中岩土体或多或少具有一定的黏性(即存在蠕变效应)，故在锚索预应力作用下岩土体的形变并不会瞬时完成，而是随着时间的延长逐渐增加，从而导致锚索的预应力也出现长期损失。朱晗迓等[22]将锚索预应力长期损失与坡体蠕变进行耦合分析，采用广义Kelvin 模型模拟边坡岩体，并采用简单的弹性体模型模拟锚索，然后，考虑锚索与岩体之间满足的变形协调关系及内力平衡条件(即边坡的变形随时间而增加的同时，锚索内的预应力也相应随之降低并最终达到稳定)，推导得锚索预应力随时间t的变化公式为

(13)

式中：P为t时刻锚索的预应力；P0为锚索的初始预应力；k为锚索预应力渐进值；r为衰减指数。

张永安[19]、景锋等[23]和王清标等[24]采用室内试验和工程监测数据验证了式(13)符合锚索预应力的变化规律，故本文采用此公式来拟合现场实测锚索预应力随时间变化数据，进而由所得参数计算任意时刻锚索的预应力，然后，将其代入式(12)中，以此来分析锚索加固条件下边坡的长期稳定性。

4 工程算例

4.1 考虑锚索预应力损失时边坡长期稳定性分析

如图2所示，贵州省某高速公路一边坡由碎石土组成，坡段分为2级，坡角β1，β2，β3均为45°，岩土体的天然重度γ=19 kN/m3。建设初期由于邻近边坡发生失稳引起该边坡出现滑动趋势，根据实验与监测数据采用强度参数反演方法可得岩土体的黏聚力c=3.559 kPa和内摩擦角φ=29.375°。同时，监测数据表明该边坡坡体内的地下水位线较低，其对边坡的稳定性影响微小，故在此不考虑地下水位。为了确保已发生滑动趋势的边坡处于稳定性状态，如图2所示，在坡体内从下至上布置了6排锚索。以坡角点为原点建立xoy轴坐标系，6排锚索在坡面上的x轴坐标分别为x1=9 m，x2=10 m，x3=11 m，x4=15 m，x5=16 m，x6=17 m，锚索的倾角均为δ=18°，单位宽度上的初始预应力均为P0=50 kN。为了获得锚索预应力长期损失，锚索施工初期在其端头埋设钢索计以此来监测锚索的预应力变化，所得近3 a的锚索预应力随时间的变化曲线如图3所示。

图2 工程边坡

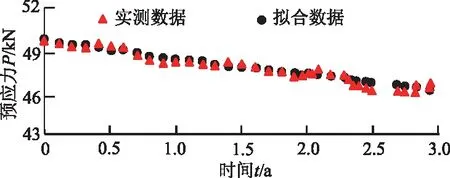
图3 实测锚索预应力随时间变化与理论模型拟合Fig.3 Curve fitting of measured pre-stress change of anchorage cable over time with theoretical model

采用式(13)指数衰减方程对锚索预应力随时间的变化数据进行拟合，可得锚索预应力实际损失计算公式，即

(14)

式中：t为时间(a)；P为锚索预应力(kN)。其中，曲线拟合系数R2=0.937。

将式(14)代入锚索加固条件下边坡稳定性计算公式中，可得到时间t从0～25 a时边坡的最小安全系数见表2。由表2可知：

(1) 对比传统极限平衡方法，本文方法所得结果较瑞典法要大，与简化Bishop法、Spencer法和M-P法颇为接近，从而验证本文方法的可行性，同时，由于本文方法可满足滑动体的所有静力平衡条件，故可得到较为严格的安全系数解答。

表2 不同时间下边坡长期安全系数对比

表3 锚索预应力损失模型中各参数对边坡长期稳定性影响

(2) 从0～25 a计算所得边坡的最小安全系数来看，预应力锚索能够确保边坡的长期稳定性。

(3) 相比初期施加锚索预应力的边坡，25 a后边坡的最小安全系数减小接近5%，因而，锚索预应力的损失对边坡的稳定性影响非常不利。

4.2 参数分析

预应力锚索仍采用图2所示布置方式，锚索倾角均为δ=18°，单位宽度上的锚索初始预应力均为P0，并取P0分别为50，55，60，65 kN。当锚索预应力损失模型中预应力渐进值k分别为0.70P0，0.75P0，0.80P0及衰减指数r分别为0.10，0.12，0.14时，分析时间t分别为0，2，4，6，8，10，12，14，16，18，20 a下边坡的稳定性，计算所得的结果见表3。

由表3可知：

(1) 在锚索预应力损失模型中，当预应力渐进值k为0.70P0～0.80P0及衰减指数r为0.10～0.14时，较初期施加锚索预应力的边坡，20 a后边坡的安全系数减小了3%～6%。

(2) 在锚索预应力损失模型中，预应力渐进值k越大及衰减指数r越小，则边坡的长期稳定性降低越少，反之则越大。

(3) 当锚索预应力衰减较快时，提高锚索的初始预应力是保证边坡长期稳定的一种有效手段。

5 结 论

基于滑动面上的应力假设，建立一种新的锚索加固条件下边坡稳定性极限平衡计算方法，并考虑锚索预应力的长期损失，通过结合锚索预应力损失模型，以此来分析锚索加固边坡的长期稳定性。将其应用于工程算例，首先对锚索预应力实测数据进行拟合以得到预应力损失模型中各参数取值，进而计算各时间点的锚索预应力，然后融入预应力损失规律研究锚索加固条件下边坡稳定性随时间变化的关系，并分析预应力损失模型中各参数对边坡稳定性的影响，由此可得：

(1) 本文方法与传统极限平衡计算方法所得结果接近，从而验证了本文方法的可行性，且将锚索预应力损失模型与极限平衡法相结合以此来分析锚索加固条件下边坡的长期稳定性是可行性的。

(2) 当锚索的预应力损失较快时，提高锚索的初始预应力是确保边坡长期稳定的一种有效手段。

(3) 在锚索预应力损失模型中，预应力渐进值k越大及衰减指数r越小，则边坡的长期稳定性越好，反之则越差。

[1] 丁秀丽，盛 谦，韩 军，等. 预应力锚索锚固机理的数值模拟试验研究[J]. 岩石力学与工程学报，2002，21(7)：980-988.

[2] 刘 润，闫澍旺，罗 强，等. 纤维砂浆增强预应力锚索锚固效果的研究[J]. 岩土工程学报，2005，27(2)：214-218.

[3] 蒋楚生，周德培，周应华. 预应力地梁锚索改善边坡受力状态的理论分析[J]. 岩土工程学报，2005，27(8)：974-976.

[4] 许 明，唐树名，李 强，等. 单锚及群锚失效对边坡稳定性影响的模型试验研究[J]. 岩石力学与工程学报，2007，36(1)：2755-2760.

[5] 李英勇，张顶立，张宏博，等. 边坡加固中预应力锚索失效机制与失效效应研究[J]. 岩土力学，2010，31(1)：144-150.

[6] 李新坡，何思明，徐 骏，等. 预应力锚索加固土质边坡的稳定性极限分析[J]. 四川大学学报(工程科学版)，2006，38(5)：82-85.

[7] 刘才华，陈从新，冯夏庭. 土质边坡预应力锚索设计方法探讨[J]. 岩土力学，2006，27(8)：1349-1352.

[8] 徐 青，徐 寅，陈胜宏，等. 复杂岩质边坡预应力锚索优化设计[J]. 长江科学院院报，2011，28(2)：32-37.

[9] 邓东平，李 亮，罗 强. 预应力锚索加固土质边坡极限平衡稳定性分析[J]. 工程地质学报，2013，21(1)：53-60.

[10]夏 雄，周德培，肖世国. 预应力锚索加固边坡稳定性的有限元评价[J]. 岩石力学与工程学报，2004，23(增1)：4489-4492.

[11]李 宁，张 鹏，于 冲. 边坡预应力锚索加固的数值模拟方法研究[J]. 岩石力学与工程学报，2007，26(2)：254-261.

[12]周 时，黄宜胜，朱 敏，等. 金川水电站导流洞进口边坡稳定性分析[J]. 长江科学院院报，2014，31(6)：89-94.

[13]赵晓彦. 类土质边坡特性及其锚固设计理论研究[J]. 岩石力学与工程学报，2006，25(3)：647-647.

[14]吴茂明，阮含婷，刘 鹭. 预应力锚索在岩土边坡工程治理中的应用[J]. 岩土工程学报，2010，32(增1)：324-326.

[15]郑筱彦. 预应力锚索对岩质边坡加固效应的数值模拟[J]. 华中科技大学学报(自然科学版)，2011，39(7)：118-122.

[16]张发明，刘 宁，赵维炳，等. 岩质边坡预应力锚索加固的优化设计方法[J]. 岩土力学，2002，23(2)：187-190.

[17]晏鄂川，吕美君，李红刚. 岩质边坡锚固参数正交优化分析及应用[J]. 山地学报，2007，25(3)：364-369.

[18]许 明，张 琴，唐树名，等. 锚索失效对边坡稳定性影响的数值研究[J]. 地下空间与工程学报，2008，4(5)：865-869.

[19]张永安，李 峰，蒋 鸥. 泥岩高边坡锚索预应力变化规律分析[J]. 岩石力学与工程学报，2007，26(9)：1888-1892.

[20]陈沅江，尹 进，胡毅夫. 软岩边坡锚索预应力定量损失规律研究[J]. 岩石力学与工程学报，2013，32(8)：1685-1691.

[21]邓东平，李 亮. 锚索预应力长期损失与岩土体蠕变耦合模型研究[J]. 长江科学院院报，2015，32(8)：65-71.

[22]朱晗迓，尚岳全，陆锡铭，等. 锚索预应力长期损失与坡体蠕变耦合分析[J]. 岩土工程学报，2005，27(4)：464-467.

[23]景 锋，余美万，边智华，等. 预应力锚索预应力损失特征及模型研究[J]. 长江科学院院报，2007，24(5)：52-55.

[24]王清标，张 聪，王 辉，等. 预应力锚索锚固力损失与岩土体蠕变耦合效应研究[J]. 岩土力学，2014，35(8)：2150-2156.

(编辑：姜小兰)A Method of Calculating the Long-term Stability of Slope Reinforcedwith Anchorage Cable in Consideration of Pre-stress Loss

DENG Dong-ping, LI Liang

(College of Civil Engineering, Central South University, Changsha 410075, China)

In actual project, slope’s long-term stability problem is caused by the loss of pre-stress of anchorage cable acting on the slope due to the creep properties of geotechnical body. To correctly estimate the long-term stability of slope reinforced with pre-stressed anchorage cable, a limit equilibrium calculation method is proposed to analyze slope stability based on the assumption of stresses on the slip surface and by integrating the model of anchorage pre-stress loss. By using this method, the factor of safety of slope reinforced with pre-stressed anchorage cable in different periods are obtained, thus the dynamic change of slope stability can be reflected. By analyzing engineering examples, the feasibility of the method is verified, and the notion that pre-stress loss of anchorage cable worsens the long-term stability of slope is proved. Moreover, parametric analysis on the influence of pre-stress loss of anchorage cable on slope’s long-term stability indicates that increasing the initial pre-stress of anchorage cable is reliable and effective to improving the long-term stability of slope.

slope; long-term stability; anchorage cable; pre-stress loss; factor of safety

2015-09-04；

2015-09-26

国家自然科学基金项目(51608541);中国博士后科学基金面上项目(2015M580702);中南大学博士后科学基金项目(201508)

邓东平(1985-),男，湖南岳阳人，博士后，从事道路与铁道工程等方面研究，(电话)13975150476(电子信箱)dengdp851112@126.com。

10.11988/ckyyb.20150747

2016,33(10):93-97,101

TU43

A

1001-5485(2016)10-0093-05