示踪法测定井中渗透流速的广义稀释模型研究

张 茜，陈建生，董海洲，滕兆明

(1.淮阴工学院 建筑工程学院，江苏 淮安 223003； 2.河海大学 地球科学与工程学院，南京 210098；3.昆山市水利局，江苏 昆山 215300)



示踪法测定井中渗透流速的广义稀释模型研究

张 茜1，陈建生2，董海洲2，滕兆明3

(1.淮阴工学院 建筑工程学院，江苏 淮安 223003； 2.河海大学 地球科学与工程学院，南京 210098；3.昆山市水利局，江苏 昆山 215300)

基于传统稀释公式和广义稀释公式存在的问题，对已有广义稀释公式在原模型基础上进行数学推导方法改进，给出理论上的严格解析解，解决了原有公式的舍入误差，简化了公式形式。以固定高度水柱为研究对象，重新建立模型，给出新的水平渗透流速计算方法。结合北江大堤文献资料给出具体应用结果，并与前人各公式进行对比分析，与考虑质量守恒和溶质弥散作用的公式结果相比误差较小，很好地反映了工程实际情况，且在数据处理和公式应用上具备简洁明了的优势，具有很好的工程应用价值。

示踪法；渗透流速；垂向流；广义稀释原理；渗漏探测

1 研究背景

地下水流动的水平流速可以通过测定注入钻孔中的示踪剂浓度变化的方法来确定，现已有许多研究成果[1-3]。Kocherin于1916年首次提出该方法原理，当时采用普通食盐溶液作为示踪剂。后来研究人员对该方法进行了进一步发展和研究[4-7]。传统示踪法原理是将示踪剂注入滤水管，并将滤水管放入检测通道,滤水管中的水柱被少量放射性示踪剂标记,地下水渗透流速影响示踪剂稀释速度,根据这种影响关系可以求出渗透流速,根据渗流速度的变化确定渗流场。此方法便于实施，可在钻孔中获取大量水文地质参数。研究理论从最初的点稀释定理到广义稀释模型到考虑质量守恒和溶质弥散等改进，但均各有不足。

本文在广义稀释模型基础上进行严格数学推导，重新给出了广义稀释模型的严格解析解，并从水柱稳定角度重新建立模型，考虑水柱总水量受到垂向流和水平流的共同影响，推导出此时的水平渗透流速计算新公式。

2 基本理论

Moser给出了在孔中无垂向流时，单井中的渗透流速计算公式[4-5]，即

(1)

式中：r为钻孔半径；t为2次测量时间间隔；α为流场畸变系数；N0为t=0时的记数率；N为t时刻的记数率，现场利用核探测器测量给出。

式(1)是传统点稀释公式，没有考虑垂向流的影响，但实际工程中垂向流的存在相当普遍，因此上述公式的应用受到了极大限制。陈建生等[7]在传统稀释法的基础上考虑垂向流的影响，给出了广义稀释公式,即

Vf=

(2)

式中：vA,vB分别为A,B两点的垂向流速;h为被测段含水层A，B两点间的水柱高度。

式(2)考虑了垂向流的影响，应用更广泛，该公式比传统点稀释公式更能揭露工程实际情况，计算结果更为可信。但由于该公式含有无穷项，在实际应用时存在舍入误差，其精度在理论上有改进空间。

樊哲超等[8]则是在广义稀释模型基础上考虑流速随时间变化而推导了近似公式,即

(3)

该公式相比广义稀释公式在形式上更为简洁，工程应用结果显示计算结果与工程实际比较贴合，但在推导中也做了近似，理论精度上依然可以改进。

叶合欣[9]从质量守恒原理出发，利用微元法重新建模推出水平渗透流速计算公式,即

(4)

式中N(z,t)为对应深度为z的点在t时刻的示踪剂计数。

式(4)模型新颖，计算结果与实际地质情况相一致，只是数据量较大时，求解较为复杂。

叶合欣等[10]又在此基础上考虑了溶质弥散作用，进一步推导了渗透流速计算公式,即

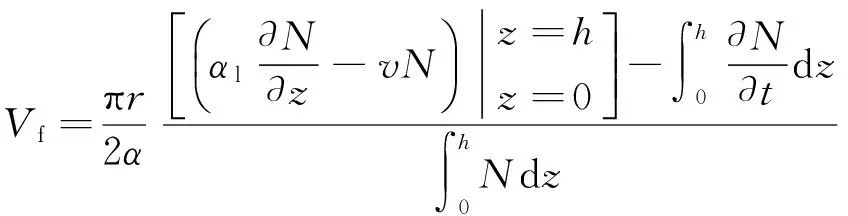
(5)

式中αl为纵向弥散度。

式(5)在式(4)的模型基础上考虑了溶质弥散作用，严密推导了流速计算公式，在工程实例中验证表明弥散作用不可忽略。虽然忽略了孔中示踪剂水平向弥散的影响，一定程度上影响了计算结果的精度，但此公式考虑因素最全面，结果最准确，但数据处理较复杂，实际应用比较繁琐。

值得注意的是在广义稀释模型推导中采用泰勒级数展开，存在舍入误差，本文在此基础上通过数学分析重新推导式(2)精确解析解的形式，并从水柱稳定角度重新建立模型，推导了新的水平渗透流速计算公式。

3 模型建立与公式的再推导

3.1 对于广义稀释公式的再推导

陈建生等[7]针对传统稀释法的局限推导了在有垂向流影响下的广义稀释公式，应用泰勒展开只取前2项，不仅加大舍入误差而且使得结果项数繁多，应用复杂[7]，为了给出解析解，本文作如下推导。

假设一定量示踪剂注入孔中水体内，止水塞间长度为h，孔径为d，水平方向流入水柱和流出水柱的水流速度分别表为vU,vD;最初产生的浓度为C，试验点地下水流稳定；孔中被标定的圆柱体积V=d2h/4(如图1)。

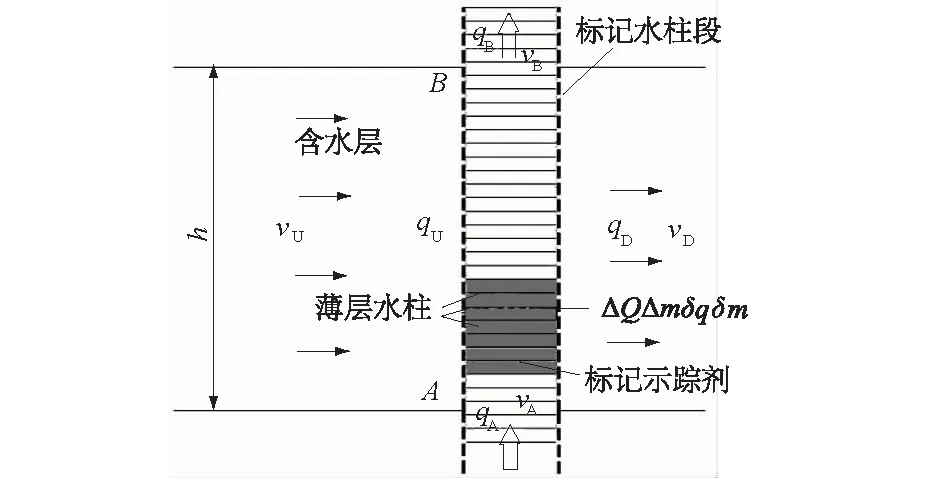
图1 广义稀释模型计算示意图[7]Fig.1 Schematic of the generalized dilution model[7]

假设条件有：示踪剂瞬时与地下水混合均匀；不考虑浓度梯度的影响，即示踪剂从体积V中逃逸仅因为水平流的影响；不考虑示踪剂弥散作用；含水层中水不可压缩；与A,B对应的含水层为均匀分布,水头相同且稳定；示踪剂在孔的同一个正截面上浓度相同，在垂直方向的分布可不均匀。

考虑水柱高度h受到垂向流vA，vB影响而改变，则Q是一个随时间变化的量，取决于A,B两点垂向流的速度差, 即

(6)

考虑高度为h的稀释水柱时,流入含水层下游的水量为

q=2rhvDt 。

(7)

通过薄层水柱内与流出含水层的水之间示踪剂浓度近似相等的关系得到

(8)

当δq→0,δm→0时，有

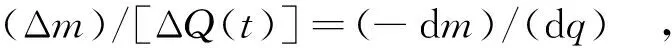
(9)

两边同时求和得到：

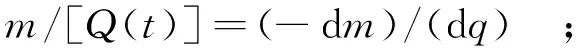
(10)

(11)

式中:δq为δt时间内流出微水柱的水量;δm为带走的溶质;△m为微水柱内示踪剂的量;△Q为水量。

积分即得式(2)，而本文发现泰勒级数展开积分结果形式复杂，应用上有舍入误差，并非精确解，为得到解析解采用分类讨论积分。

当vA=vB时，有：

(12)

(13)

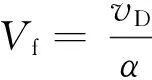
当vA≠vB时，有：

(14)

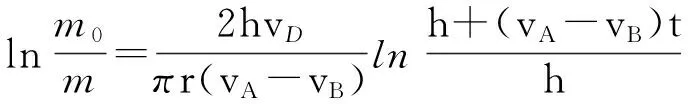
(15)

得到水平渗透流速计算公式为

(16)

综上可得广义稀释公式可以统一表达如下：当vA=vB时，即式(1)；当vA≠vB时，即式(16)。

结合工程实际情况可以预见，垂向流速对于水平渗透流速的影响是连续的，即水平渗透流速不应在垂向流vA=vB时发生突变，因此其表达式也应该是垂向流的连续函数，即应该满足对于垂向流速的连续性。鉴于此，对式(16)作连续性验证。

为方便表示，设vA-vB=vv，代入式(16)则

(17)

当vA→vB时，有vv→0，于是

(18)

化简即得点稀释公式，即式(1)。可见式(16)在vA=vB时是点稀释公式，满足连续性要求，与事实吻合。于是广义稀释公式可以统一表达为式(16)。与式(2)对比，改进之处在于原有广义稀释公式应用泰勒展开，形式复杂，且只是近似意义上的解，本文式(16)则是通过分类讨论，直接进行积分运算得到，形式简单，且为精确解析解，在工程应用时避免繁杂多项带来的舍入误差。

图2 水柱稳定模型计算示意图Fig.2 Schematic of water column stability model

3.2 模型的重新建立与推导

上一节所得式(16)是对广义稀释公式积分方法的改进，在钻孔内微水柱中溶质浓度与该时刻流出微水柱的水所带走的溶质的浓度近似相等，在钻孔内选取dz高度的微水柱，如图2所示，假设条件同上，为使示意图具有一般代表性，与图1所示含义相同，A处代表流入水柱的速度，B处代表流出水柱的速度，以便后续探讨流速不同情况的适用条件。

上一节的推导改进都只考虑了流出水柱的水量q受到水平流速的影响，而工程实际情况是垂向流的存在对q也产生影响，取固定高度为h的水柱为研究对象，考虑水柱中流出水量q受到垂向流速和水平流的共同影响，则q的表达式为

q=2rhvDt+πr2(vB-vA)t ；

(19)

dq=2rhvDdt+πr2(vB-vA)dt 。

(20)

则Q为相对应高度h的整孔水柱水量,即

(21)

水量平衡有

(22)

将式(20)和式(21)代入式(10)得：

(23)

(24)

(25)

式中各变量意义与前文同，可以看到式(1)正是式(25)的一个特例。

可以发现，式(16)比式(2)有了理论推导上的改进，但计算模型一样，考虑高度h的水柱内，总水量Q受到垂向流的影响，流出水柱的水量q受到水平流速的影响，而实际上对于h高度内的水柱总量来说，流出的水量q受到水平流和垂向流的混合影响，式(25)就是考虑了这种共同影响而推得的结果，应是更接近工程实际情况的解。

4 公式适用条件

本文所推导的式(16)和式(25)是对广义稀释公式研究的改进，但也有一定适用条件，在模型建立中都讨论了垂向流的影响,即vA=vB时，若垂向流量相对水平流量太大，会给计算结果带来较大误差，定量研究意义不大，一般在垂向流量小于水平流量时适用性越好，当然越小越适用；vAvB时，为吸水层，此时应区分吸水模式，若是辐射状径向吸水，公式不适用，若垂向流与水平流量接近，则公式只能做定性参考，定量化意义不大，若垂向流远小于水平流量，则在需要考虑流场畸变时，公式基本适用。

表1 试验孔示踪探测结果(孔半径r=0.035 m，α=2)

5 工程实例的对比分析

通过式(1)—式(5)、式(16)、式(25)应用于工程实例的结果对比来说明式(25)的合理性，采用文献[7]中某钻孔示踪剂探测资料，试验孔位于广州清远石角镇北江大堤，通过投放并测量示踪剂浓度得到7条曲线，如图3所示。

图3 钻孔中示踪剂浓度变化图[7]Fig.3 Variations of tracer concentration[7]

将相邻峰值之间的含水层作为一个分层，共分为5层，为了提高垂向流速计算的精度，将两峰值之间计算出的垂向流速看作其连线中点的流速，然后用多项式来拟合各个中点的值，利用得到的多项式关系来推求峰值深度对应的垂向流速值，见图4。分别用式(1)—式(5)、式(16)、式(25)计算各层水平渗透流速，见表1、表2和图5。

图4 垂向流速拟合曲线Fig.4 Curve fitting of vertical velocity

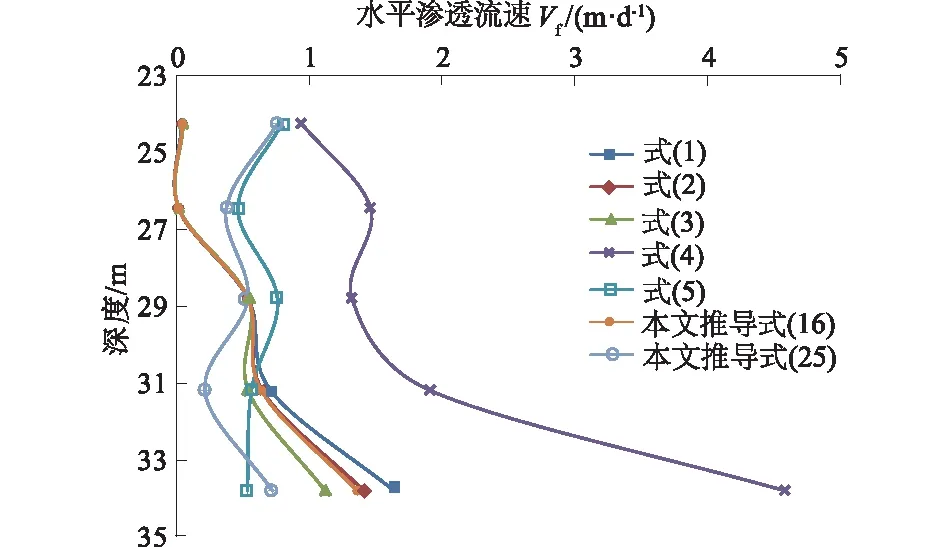
图5 各式计算结果对比Fig.5 Calculation results of the formulas

通过图5可以发现，式(1)和式(2)结果很相近，但在整孔深度范围内发现水平流速大小相差较大，与事实不符，因为式(1)没有考虑垂向流，而本工程资料显示该孔垂向流显然不可忽略。

通过式(2)与式(16)对比可见两式结果较为相近，式(16)更简洁且更严谨，而式(3)则与式(16)相比偏离较大，可见式(3)所做的考虑并不必要，且由于近似推导而加大了误差。

从整体上发现，式(1)、式(2)、式(3)、式(16)都是广义稀释模型的已有形式，本文式(16)最严谨且方便应用，但相比式(4)、式(5)，式(16)所得结果相差较大，最大数量级差别达到2级，与工程实际情况不符，而式(5)则比式(4)多考虑了弥散作用，因此计算流速结果显示更为均匀，与地质资料表明的含水层性质均匀较为一致，更为可信。

表2 各公式计算结果

对比式(4)、式(5)、式(25)的结果发现流速比较均匀，且地质资料[11-12]显示，该层颗粒分布较均匀，渗透性差距不大，因此在稳定水位下的水平渗透流速也应相近，正与以上公式计算结果相符合，而式(4)显示最大渗透流速与最小渗透流速比值为4.9，仍处于同一数量级，而式(7)相应之比为3.59，式(5)则最为稳定，相应之比为1.7。从图5可见式(25)与式(5)整体趋势较相近，即与同时考虑质量守恒和溶质弥散作用的公式本质上相近，比较合理，较为真实地体现了整个含水层中的局部差异和整体均一性。说明式(25)计算结果可信，符合实际，且更客观反映了工程实况，相比式(5)在形式上简便易懂，操作方便，避免数据处理的繁冗和参数求解的麻烦，不仅是严格解析解，而且具有数据处理简便的优势，适应工程应用需要。

6 结 语

在水文地质调查等方面，应用示踪法测定地下水渗透流速的手段取得了极大成功，但传统点稀释公式受到垂向流等条件的限制，后来发展的广义稀释模型、基于示踪剂质量守恒模型、考虑溶质弥散作用模型等都各有不足。本文在前人工作基础上对广义稀释公式重新推导，给出了严格解析解，解决原有公式存在的舍入误差，并建立水柱稳定模型，推导了新的水平渗透流速计算公式。与前人成果进行对比分析，能够得到更为丰富的更为贴近实际地质情况的含水层水平流速变化信息,客观反映了工程实际情况，结果比较合理，且形式简单，应用方便，避免了数据处理的繁冗和参数求解的麻烦，具有数据处理优势，在工程应用中简便易行，为获取和求解一些水文地质参数发挥一定工程应用价值。

[1] 刘光尧,陈建生.同位素示踪测井[M].南京:江苏科学技术出版社,1999.

[2] 叶合欣,陈建生,李兴文.同位素水文学示踪法在探测堤坝渗漏研究中的应用[J].西部探矿工程,2006,18(5):28-31.

[3] 刘光尧.用放射性同位素测定含水层水文地质参数的方法(上)[J].勘察科学技术,1997,(1):21-27.

[4] DROST W D, KLOTZ D, KOCH A,etal. Point Dilution Methods of Investigating Groundwater Flow by means of Radioisotopes[J]. Water Resources Research,1968,4(1):125-146.

[5] 陈建生.岩体力学同位素示踪理论与方法研究[D].南京：河海大学，2000.

[6] 陈建生,李兴文,赵维炳.堤防管涌产生集中渗漏通道机理与探测方法研究[J].水利学报,2000,(9):48-54.

[7] 陈建生,董海洲.井中测定流速广义示踪稀释物理模型[J].水利学报,2002,(9):100-107.

[8] 樊哲超，陈建生，董海洲，等.广义示踪稀释模型中水平渗速计算公式再讨论[J].岩土工程学报,2006，28(4)：432-435.

[9] 叶合欣.基于示踪剂质量守恒的测流模型研究[J].四川大学学报(工程科学版),2007,39(5):26-30.

[10]叶合欣，陈建生，童海滨，等.考虑示踪剂弥散作用的渗透流速计算方法[J].水利学报,2008，(2):240-244.

[11]叶合欣,陈建生,李兴文.水质模糊聚类及环境同位素在探测某堤基渗漏通道中的应用[J].工程勘察, 2005,(1):22-25.

[12]叶合欣, 黄春华，陈建生,等.北江大堤石角管涌多发段基岩地质条件分析[J].水文地质工程地质,2003,30(4):76-78.

(编辑：陈 敏)Modified Generalized Dilution Model of Determining PermeabilityVelocity in Wells by Tracer Method

ZHANG Xi1，CHEN Jian-sheng2， DONG Hai-zhou2，TENG Zhao-ming3

(1.School of Architectural Engineering, Huaiyin Institute of Technology, Huaian 223003,China; 2.School of Earth Science and Engineering, Hohai University，Nanjing 210098,China; 3.Water Conservancy Bureau of Kunshan, Kunshan 215300, China)

On the basis of traditional and generalized dilution formulas, we took the existing problems into consideration and deduced again based on the original model, removing the rounding errors of the original formula by giving the theoretically strict solutions. With water column of constant height, we deduced the new formula of horizontal seepage velocity. Taking the document data of Beijiang dike as an example, we calculated the results by using the proposed formula and compared the results with those by previous formulas. We found that our new formula result has small errors compared with those considering the mass conservation and solute dispersion effect. The proposed formula reflects the actual project well and has the advantage of simple form in application and data processing, with good engineering application value.

trace method; permeability velocity; vertical flow; generalized dilution principle; leakage detection

2015-08-05 ；

2015-10-29

国家自然科学基金青年基金项目(50809024)；江苏省自然科学基金项目(BK2009343)；教育部博士点基金项目(20090094110007)

张 茜(1985-)，女，江苏宿迁人，助教，硕士，主要从事土木结构和岩土体渗流计算与测试研究，(电话)0517-83591177(电子信箱)zhangxi_008@sina.com。

陈建生(1955-)，男，江苏泗阳人，教授，博士，博士生导师，主要从事水库堤坝渗漏探测与加固关键技术，地面突水、矿山透水灾害致灾机制与预警，隧道、边坡的稳定性监测和分析等研究，(电话)025-83787734(电子信箱)jschen@hhu.edu.cn。

10.11988/ckyyb.20150662

2016,33(10):126-130,139

TU43

A

1001-5485(2016)10-0126-05