基于回声状态网络的音频频带扩展方法

刘 鑫,鲍长春

(北京工业大学电子信息与控制工程学院，北京 100124)



基于回声状态网络的音频频带扩展方法

刘 鑫,鲍长春

(北京工业大学电子信息与控制工程学院，北京 100124)

宽带音频通信系统对传输信号有效带宽的限制会降低重建音频的主观质量和自然程度.本文提出了一种基于回声状态网络的宽带向超宽带音频盲目式频带扩展方法.该方法借助回声状态网络来模拟音频信号高低频频谱参数间的映射关系，并依据网络模型中的时延递归结构连续更新系统状态来近似描述音频特征的时域演变过程，有效地估计了高频成分的频谱包络.同时，结合频谱复制方法得到的高频频谱细节，该方法实现了宽带向超宽带音频的有效扩展.测试结果表明，本文所提方法提升了宽带音频的听觉质量；对于多数测试数据，该方法在静态和动态失真方面获得了优于高斯混合模型扩展方法的扩展性能.

音频编码；音频频带扩展；回声状态网络；频谱复制

1 引言

受到通信网络传输速率的限制，感知音频编码方法通常限制音频有效带宽，优先编码其低频成分，以提升编码效率[1].然而，人们并不满足于现有的宽带音频通信质量，并期望获得更加明亮而富有表现力的音频服务.为此，如何使宽带音频系统获得或接近超宽带音频的主观听感成为了音频通信领域亟待解决的问题.

作为有效的音频增强方法，频带扩展在不改变信源编码和网络传输的前提下，在解码器重建信号中人为地增添高频成分，以实现信号带宽的扩展[2].近十几年来，相关学者从频谱包络和频谱细节两个方面提出了众多频带扩展解决方案.非正式听力测试结果表明，高频频谱包络估计的准确性对重建音频听觉质量的提升十分重要[3].因此，可借助统计学习方法拟合高低频频谱间的映射关系.1994年，Y M Cheng等学者提出利用统计恢复函数来预测高频频谱，初步改善了重建音频的质量[4].同年，H Carl借助低频特征和高频频谱包络的联合码本模拟两者的一对一映射，提出了基于码本映射的频谱包络估计方法[5].该方法降低了扩展后音频频谱失真.在其基础上，有学者相继提出了内插、软判决和分裂码本映射等方法，以降低单一码本造成的频谱失真[6～8].2000年，K Park和H S Kim提出了基于高斯混合模型(Gaussian mixture model,GMM)的频谱包络估计方法[9]，该类方法利用GMM来近似高低频特征联合概率密度，并在均方误差最小准则下实现了高频频谱包络的估计.该方法基于软聚类的连续统计模型，抑制了码本映射等离散映射方法重建音频频谱的非自然间断.此外，有学者利用前向神经网络来估计高频频谱包络[10,11].B Iser等学者则将前向神经网络方法和码本映射方法进行了对比，结果表明两者扩展后音频的听觉质量没有显著差异，而前向神经网络方法计算复杂度明显降低[12].

上述方法均着重去发掘当前音频帧内部高低频的相关性，更侧重于频谱静态特性的展现.而P Jax等利用隐马尔科夫模型来模拟音频频谱包络时域动态演变[13,14]，将帧间相关性引入到频谱包络估计中[15,16].但是，该方法仅利用离散的状态来分段模拟实际音频频谱的时间演变，其重建音频仍然存在动态失真.为此，有必要在频谱包络估计中引入连续动态模型.本文提出了一种基于回声状态神经网络(echo state network,ESN)的频谱包络估计方法，借助递归结构的非线性特性连续更新系统状态，进而描述音频特征的动态演变，并依据高维空间的线性映射来拟合高低频特征参数间的非线性关系.结合基于频带复制的频谱细节扩展方法，实现了宽带音频向超宽带音频的有效扩展.

2 基于回声状态网络的音频频带扩展方法

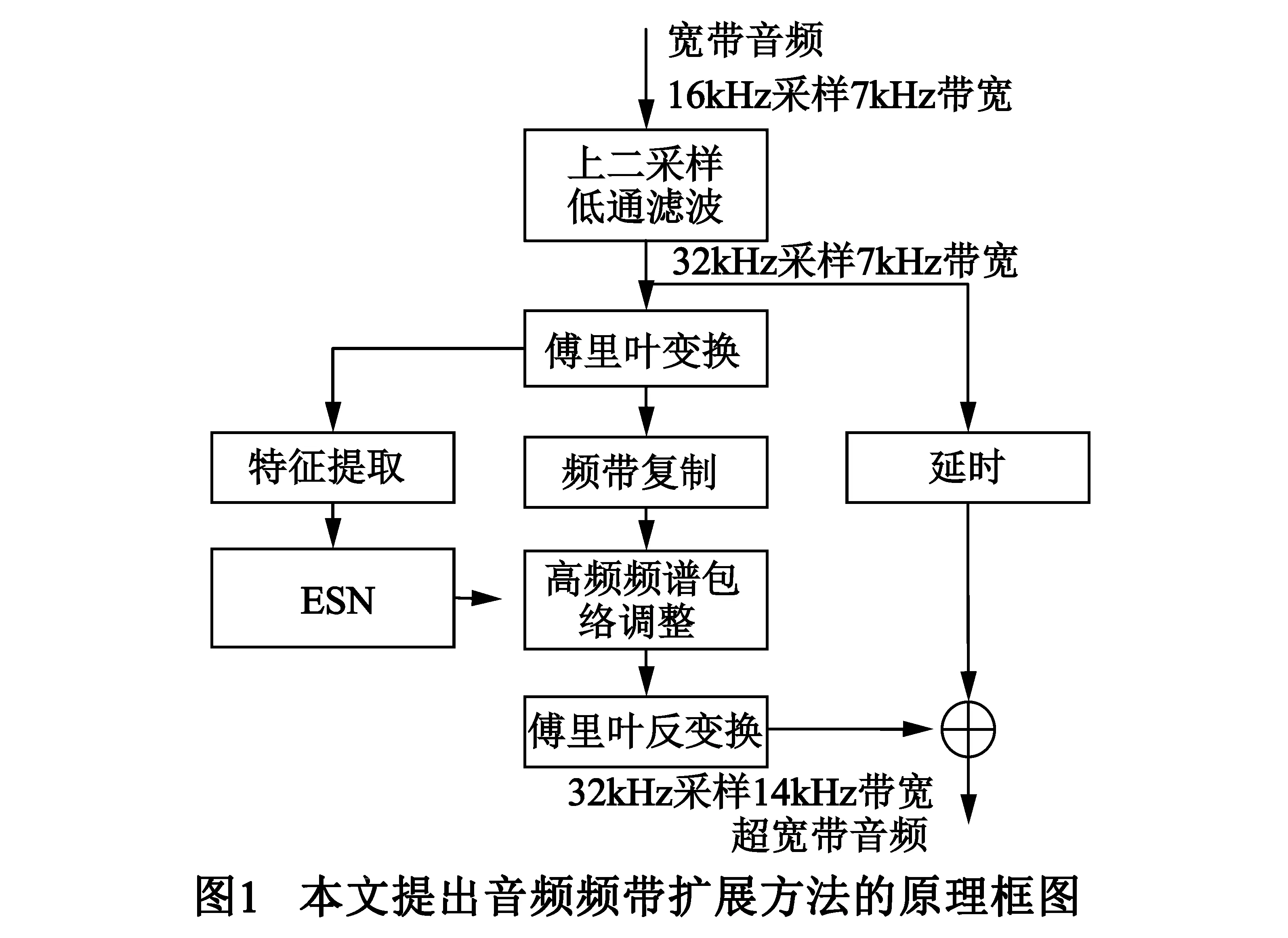
本文所提方法的基本原理如图1所示.输入信号为16kHz采样7kHz带宽的宽带音频信号.该信号首先经过上二采样和低通滤波，获得32kHz采样7kHz带宽的音频信号，并按照32ms帧长、16ms帧移分帧，加汉明窗.然后，加窗后信号swb(i),i=0,…,1023经过离散傅里叶变换(Discrete Fourier transform，DFT)转换到频域，并在梅尔频率尺度上利用三角滤波器组将64～7000Hz频率范围内的音频频谱A(k)均匀地划分为20个通道，进而提取20维梅尔频率倒谱参数(Mel Frequency Cepstral Coefficient,MFCC)FMFCC(i),i=0,…,19.接下来，对提取得到的FMFCC进行区间归一化处理，并输入到预先训练好的ESN中实现高频频谱包络的估计.此处，高频频谱包络采用7～14kHz范围内4个不交叠非均匀子带的均方根值FRMS(i)，i=0,…,3表示，如下式所示.

(1)

式中，A(k)为音频频谱幅度值，h(i)和l(i)分别为第i个子带上下限频率对应的频点序号.各子带的中心频率分别位于8470Hz、9338Hz、11653Hz以及13657Hz.

高频频谱细节则采用频谱复制方法，将低频频谱直接复制到高频频谱，并根据估计得到的FRMS来调整扩展后高频频谱包络.最终，利用离散傅里叶逆变换和叠接相加技术将重建高频转换到时域中，并结合适当延迟后的宽带音频信号，重建出超宽带音频.

2.1 基于ESN的频谱包络估计

令FX(m)表示第m帧宽带音频的MFCC，其维数为dX=20，FY(m)表示第m帧高频子带均方根值，其维数为dY=4.通过FX估计FY的过程可用某个映射函数F(·)表示，

FY=F(FX)

(2)

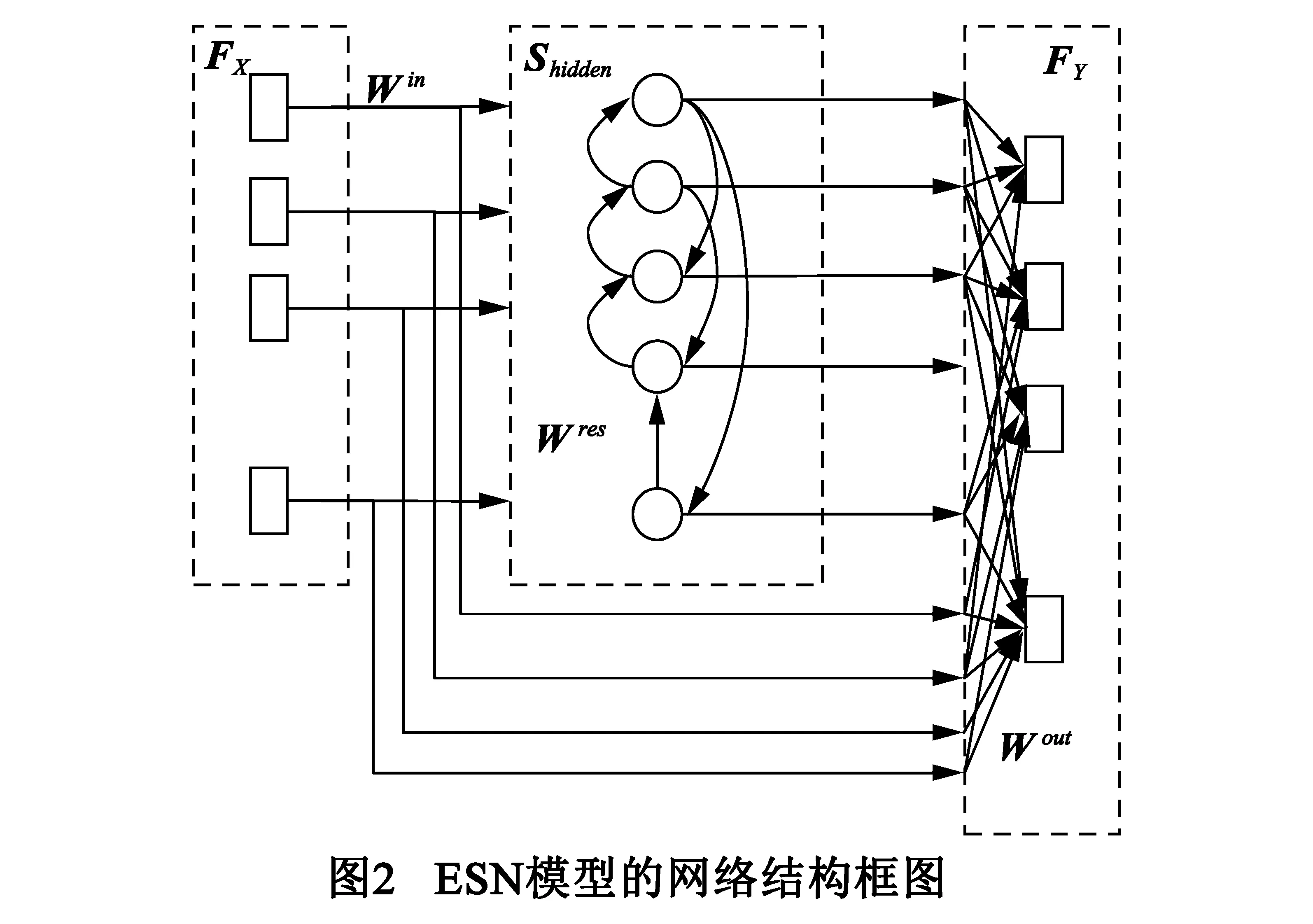
为了逼近高低频参数间的真实映射，本文引入了ESN[17～20]，其网络结构如图2所示.首先利用隐含层中预生成的大规模递归结构将FX转换到高维空间中，进而借助高维隐含状态Shidden的连续更新来描述FX的动态演变.在此基础上，ESN分别从FX与Shidden中获取音频低频成分的静态和动态特性，进一步借助高维空间中的线性映射逼近FX与FY间的非线性映射.

2.1.1 ESN的数据模型

ESN可分为隐含状态更新和高维空间映射两个部分.

隐含状态更新中，ESN采用leaky-integrated函数作为隐含层的非线性激活单元.该函数结合非线性变换和时间递归结构，实现对隐含状态Shidden的动态更新，具体过程[19]如下式所示，

(3)

(4)

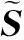
输入权值矩阵Win表征了FX与Shidden间的关联性，其维数为dS×(dX+1).通常，Win中元素的取值范围限制在[-ain,ain]之间.若ain趋近于0，leaky integrated函数呈现近似线性特性.随着ain增大，FX在驱动Shidden的更新过程中则呈现出更多的非线性特性，进而提升ESN对高低频频谱真实映射的拟合能力.

递归权值矩阵Wres则表征了前后帧Shidden的关联性，其维数为dS×dS，实际应用中可通过人为调节Wres谱半径ares的大小来控制ESM递归结构的稳定性.此外，ain和ares共同决定了Shidden更新过程中FX和Shidden(m-1)的相对重要性.若ares较大，Shidden(m-1)在状态更新过程的作用中更为显著，网络结构会保留FX中更多的长时相关性，有助于改善重建高频频谱包络的时间连续性.

隐含层内部神经元间通常采用稀疏递归链接的方式.Wres中元素的稀疏程度fsparsity表示了Shidden内相互之间存在连接的神经元占所有神经元总数目的百分比.理论上讲，ESN采用稀疏的Wres能够改善网络泛化能力，提升高频频谱包络估计的准确性，并进一步减低ESN对模型参数存储的需求.

参数α为泄漏速率，它表征了Shidden的动态更新速率.当α=1时，leaky-integrated非线性函数退化为tanh函数；随着α逐渐减小，ESN中Shidden的更新会明显减慢，增加了递归网络的短时记忆长度.

经过leaky-integrated非线性单元的逐帧更新，Shidden获取了FX的动态特性.在此基础上，ESN网络将FX和Shidden相结合构成高维特征矢量，进一步借助高维空间中的线性映射来逼近FX与FY间的非线性映射[17]，如下式所示，

2.1.2 ESN的训练方法

根据上述模型，可采用适当的训练方法来求取ESN中的模型参数(Win、Wres和Wout).传统基于梯度下降的训练方法并不能保证ESN的稳定性，并且计算复杂，收敛慢.鉴于此，有学者针对ESN网络结构提出了一种启发式参数训练方法[17].

该方法首先在初始化阶段随机生成Win和Wres.由于Wres的矩阵谱半径ares直接影响了ESN的稳定性，因此需要根据实际应用条件对其人为调整[17].令W为一个随机生成的稀疏矩阵，λmax为W的谱半径，则Wres可以表示为，

(6)

相关研究结论[21]表明，递归神经网络的训练中输出权值矩阵会根据梯度变化而迅速改变，隐层内部连接的权值则呈现出高度耦合，其变化较为缓慢.ESN隐含层中递归节点数目庞大，网络复杂，因此在参数训练中Win和Wres呈现出显著的强耦合性，不随梯度剧烈改变[17].鉴于此，启发式训练方法可令Win和Wres在其后参数训练中保持固定不变，而通过修正Wout的方式调整ESN模型对FX和FY间非线性映射的拟合能力，简化递归神经网络的训练过程.

假定FX(m)和FY(m)分别是训练数据集中的宽带音频特征和高频频谱包络参数，m=0,1,…,Ntrain-1为音频帧序号，Ntrain为数据总帧数.参数训练方法可以依据式(3)、式(4)来驱动ESN实现对Shidden(m)的逐帧更新.在实际应用中，通常会随机设置Shidden(-1)，这样必然会影响网络的稳定性.为此本文设定了网络稳定时间T0=200ms，并假设当ESN超过该时刻后达到渐进稳定.从T0开始，逐帧收集FX(m)、Shidden(m)以及FY(m)，并分别构成状态收集矩阵B和期望输出矩阵Q.其中，B的维数为(1+dX+dS)×(Ntrain-T0)，其每列元素为[1,FX(m)T,Shidden(m)T]T，包含了每一帧的宽带音频特征的静态和动态特性；而Q的维数为(dY)×(Ntrain-T0)，其每列元素为该帧音频的FY(m).

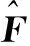
(7)

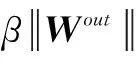
对上式求解，可以得到最终的Wout，

Wout=QBT(BBT+βI)-1

(8)

式中，I为单位矩阵.

根据所获得的Wres、Win和Wout，可构建出一个完整的ESN.在实际扩展中，利用每一帧提取的FMFCC连续更新Shidden，进而借助高维线性映射有效估计高频频谱包络.

2.2 高频成分的重建

本文采用频谱复制来扩展高频频谱细节，即将0～7kHz范围内的频谱细节直接复制到7～14kHz的高频中.而低频频谱细节可采用归一化幅度谱参数Anorm(k),k=0,…,223,来表示，

(9)

式中，A(k)为音频幅度谱；FRMS-WB(i)为低频子带均方根值，其计算方式与式(1)相近，可初步描述音频低频频谱包络.此处，为了保证Anorm(k)的频谱平坦度，低频频谱子带采用均匀划分方式.0～7kHz的频率范围分为为14个子带，每个子带包含Nsubband=16个频点.那么，经过频带复制，扩展后高频频谱细节可表示为，

Anorm(k)=Anorm(k-224),k=224,…,447

(10)

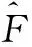
(11)

式中，Subband(k)表示第k个频点所在高频子带的序号.

高频频谱相位θ(k),k=224,…,447,同样采用频谱复制方法获得，如下式所示，

θ(k)=θ(k-224),k=224,…,447

(12)

最终，根据IDFT，高频频谱转换到时域.而上采样后的宽带音频经过适当的延时后，与人为生成的高频信号相结合，重建出超宽带音频.

3 回声状态网络模型参数对扩展性能的影响

本文针对2.1.1节中涉及到的网络参数(Win缩放因子ain、Wres谱半径ares、Wres稀疏度fsparsity、leaky-integrated函数泄漏率α、岭回归正则因子β、储备池规模dS等)对ESN方法性能的影响进行了初步测评.ESN训练数据源自于4小时时长现场音乐会转录的无损音频，其中包括对话、音乐、人声演唱、实况背景音效等类型.声音采样率为32kHz，有效带宽为14kHz，采用16比特PCM进行存储.该超宽带数据库经过低通滤波、下采样和时间延迟进一步获得平行宽带数据库.分别从平行宽带和超宽带音频数据中提取20维MFCC和4维高频子带均方根参数作为ESN的输入特征矢量FX和期望输出矢量FY.所获得的50%样本数据用于模型训练，而另50%数据用于性能测试.

此外，本文选择了7～14kHz频率范围内频带扩展方法处理后音频信号与原始超宽带音频信号的对数谱失真(log spectral distortion,LSD)作为客观测度对ESN的预测准确度进行评价.LSD可以直接利用DFT功率谱计算得到[22]，如下式所示，

(13)

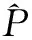
(1)Win缩放因子ain

缩放因子ain决定了leaky-integrated激励函数的非线性特性.本文利用实验测试的手段来经验性地确定ain.分别设定ares=1、fsparsity=1、α=1、β=1、dS=4×dX=80，并在LSD测度下针对不同的ain值进行测试，如表1所示.当ain=1/8时，ESN获得最小的LSD.而当非线性函数趋近于线性或二值函数时，LSD值均会增加.由此可见，FX与FY之间确实存在一定的非线性关系.

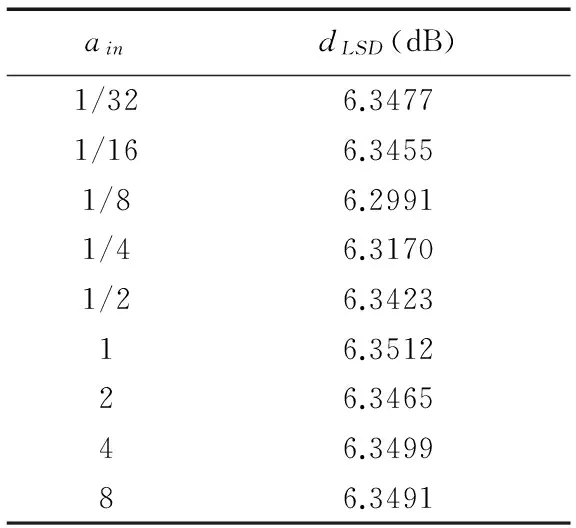
表1 不同的ain下ESN模型的LSD值

(2)Wres谱半径ares

ares是Wres的谱半径，它决定了ESN的稳定性.本文借助LSD测度经验性地确定Wres谱半径ares，如表2所示.本文将其他参数分别设定如下，ain=1/8、fsparsity=1、α=1、β=1、dS=4×dX=80.当ares=0.6时，模型的LSD值最小；而当ares>1时，ESN的LSD值逐渐增大，部分帧估计的高频频谱包络和原始音频具有较大的差异；而当ares较小时，储备池中内部神经元的递归作用减弱，也会导致模型的LSD有所增加.由此可见，在保证ESN网络稳定的条件下，适当引入递归特性有助于提升ESN对宽带音频特征时间动态特性的描述能力.

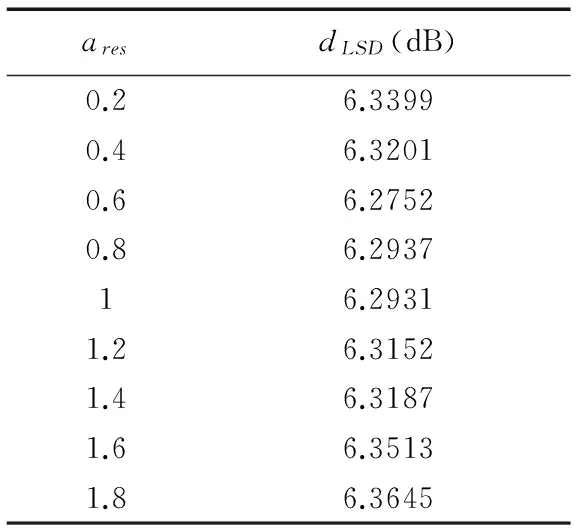
表2 不同的ares下ESN模型的LSD值

(3)Wres稀疏度fsparsity

令其他参数分别设定为，ain=1/8、ares=0.6、α=1、β=1、dS=4×dX=80，本文进一步针对稀疏度fsparsity进行评价，如表3所示.当隐藏状态神经元之间采用全递归连接的方式，网络模型获得最小的LSD值；而在fsparsity较低的情况下，LSD会有所增加；而当fsparsity低于10%左右时，LSD值将降低到6.28dB附近.由此可见，增加Wres的稀疏程度不能改善ESN重建音频的客观质量.然而，采用较小的fsparsity(如0.025)可以在不过多加重LSD的前提下提升ESN的训练效率，并降低模型的存储需求.

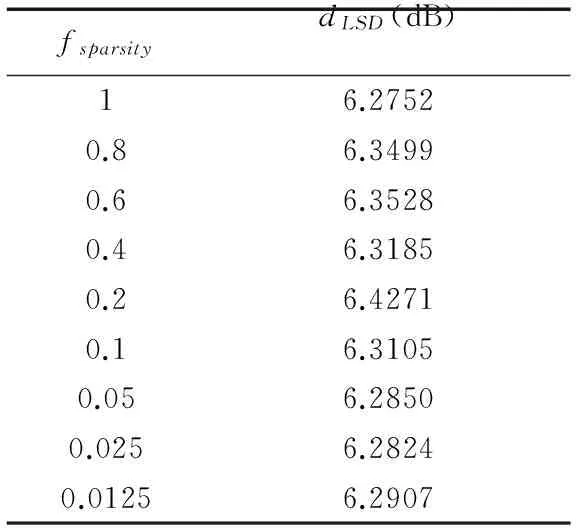
表3 不同的fsparsity下ESN模型的LSD

(4)leaky-integrated函数泄漏率α

泄漏率α表征了Shidden(m)的动态更新速度.本文分别设定ain=1/8、ares=0.6、fsparsity=1、β=1、dS=4×dX=80，并测试了不同α对模型性能的影响，如表4所示.结果表明，α对LSD值的影响不大，即Shidden更新过程中涉及的FX长时记忆性对ESN的性能没有明显的改进作用.

(5)岭回归正则因子β

Wout可采用岭回归计算，以防止过度拟合.设置ain=1/8、ares=0.6、fsparsity=1、α=1、dS=4×dX=80，则β与LSD间的关系如表5所示.基于岭回归方法训练模型的LSD值明显低于线性回归方法(β=0)；当β=3.5时，ESN获得最优的性能.

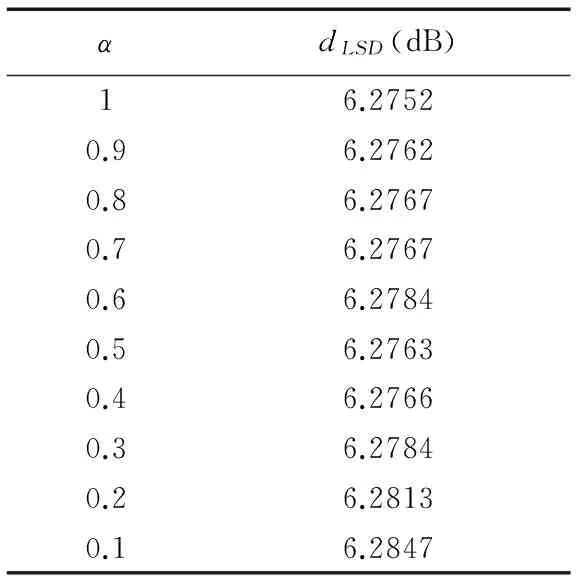
表4 不同的α下ESN模型的LSD值

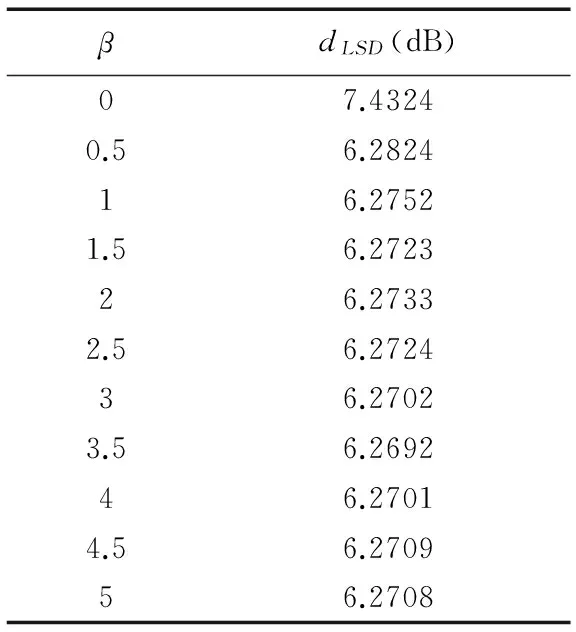
表5 不同的β下ESN模型的LSD值

(6)隐含层规模dS

一般来说，如果采用适当的正则化方法来抑制过度拟合，那么dS越大可获得更好的性能.ESN的参数训练方法计算简单，因此dS通常在数百左右.然而考虑到实际存储需求，仍需适当控制其规模.令ain=1/8、ares=0.6、fsparsity=1、α=1、β=3.5，本文针对网络隐含层规模进行了探讨，如表6所示.LSD测试结果表明，随着dS逐渐增大，ESN方法所重建高频频谱失真逐渐降低，而其最小值出现在dS=24×dX=480处.

表6 不同的dS下ESN模型的LSD

综合上述评测结果，本文最终确定网络参数为ain=1/8、ares=0.6、fsparsity=1、α=1、β=3.5、dS=24×dX=480.

4 性能评价与测试结果

本文首先根据扩展后超宽带音频与原始超宽带音频高频子带均方根值之间的均方误差来初步评价高频频谱包络估计方法的准确性.在此基础上，进一步从对数谱失真(log spectral distortion,LSD)、双曲余弦测度(COSH)和差分对数谱失真(differential log spectral distortion,DLSD)三个方面对所提方法和基于GMM的频带扩展参考方法重建音频的客观质量进行对比.此外，本文依据主观偏爱测试和计算复杂度对频带扩展方法进行评价.

4.1 参考算法与音频数据

除了频谱包络估计模块，GMM参考方法和图1所示的扩展原理基本一致.在GMM方法中，每帧提取的MFCC输入到基于GMM的最小均方误差估计器.其中GMM包含128个高斯分量，并采用对角方差矩阵.而高频频谱细节同样采用频谱复制方法.

参考方法与本文方法所需训练数据均源自4小时现场音乐会转录的无损音频，其中包括对话、不同类型的音乐、人声演唱以及现场背景等.相关测试结果表明，进一步增加训练数据的长度对频带扩展方法主客观性能的提升并不明显.对该音频数据进行重采样和时间对齐，可分别获得宽带和超宽带音频的平行数据库.所有数据在进行处理前，其声音水平需归一化至-26dBov.此外，本文从MPEG音频质量主观听觉测试数据库中选择了15段音频作为测试数据，包含了流行音乐、器乐独奏、交响乐片段以及语音等不同类型.这些数据长度限制在10～20s范围内，采样率为32kHz，有效带宽为14kHz.该数据通过截止频率为7kHz的低通滤波和下采样转换为宽带信号，并将其声音水平归一化到-26dBov后作为频带扩展方法的输入.下面本文分别根据频谱包络估计误差、扩展后音频主客观质量以及计算复杂度对算法性能进行详细分析.

4.2 频谱包络估计误差

为了验证高频频谱包络估计的准确性，本文首先依据重建音频与原始音频高频频谱包络间的均方误差对本文所提方法和GMM参考方法进行了对比.此处，频谱包络估计的均方误差可以定义如下，

(14)

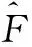
表7给出两种方法对于不同类型音频信号高频频谱包络估计误差的结果.其中，乡村、爵士和摇滚音乐高频频谱能量明显高于其他类型音频，因此不同估计方法重建高频频谱包络的平均误差较高.小提琴独奏和交响乐音频频谱成分则多集中在低频，随着频率增加其高频逐渐暗淡，因此这两种音频频谱包络估计的误差相对较低.而语音中部分清音高频能量较强，其频谱包络的估计值和原始包络间同样存在较大的误差.

表7 不同扩展方法高频频谱包络估计的误差

总体上讲，本文方法能够有效地估计出高频成分的频谱包络，其频谱包络估计误差的平均值较参考算法降低了3.15左右.对于爵士音乐，ESN方法重建音频高频能量丰富，其频谱包络更接近于原始音频，而GMM方法重建高频频谱则相对暗淡，进而造成了较为明显的估计误差.而对于乡村音乐和交响乐，ESN方法重建高频频谱整体能量偏高，其频谱包络估计误差高于参考算法.

4.3 客观质量测试

此外，本文进一步利用LSD、COSH以及DLSD三种测度对不同方法进行客观评价，结果如表8所示.

4.3.1 对数谱失真

本文分别对所提方法和参考方法重建音频进行了LSD比较，如表8所示.与频谱包络估计误差分析结果相近，ESN方法LSD的平均性能略优于GMM方法.对于摇滚音乐、小提琴独奏、语音信号，两种方法LSD值的差异均在±0.5dB范围内.而两者LSD差异较大的是爵士音乐，这种类型音频信号高频能量比较丰富，并且在时域上低音贝斯伴奏使得该音频存在明显的暂态成分.GMM重建高频频谱比较平坦，而ESN方法重建频谱包络更接近于原始音频，因而获得了较低的LSD.而对于交响乐和乡村音乐，ESN重建高频的整体能量略高，尽管主观听感上音频更为明亮，但是其LSD高于GMM方法重建音频.

表8 不同扩展方法重建音频的客观失真测试结果

4.3.2 双曲余弦测度

(15)

作为距离测度，dIS并不具有对称性，因此本文选择了COSH测度作为修正失真测度来描述重建音频的感知失真.COSH测度dCOSH定义如下[23]，

(16)

COSH测度只针对7～14kHz频率范围进行计算，且每段测试数据上所有帧测度的平均值作为最终的COSH测度.两种频带扩展方法重建音频的COSH值比较结果如表8所示.在整体上，ESN重建音频的COSH值与GMM方法比较接近.ESN方法在爵士音乐和语音信号上重建音频的客观质量要优于GMM方法，而在乡村音乐上则略低于参考方法.综合以上两项性能对比结果，可以获得结论：ESN静态客观失真相比GMM方法略有提升.

4.3.3 差分对数谱失真

音频频谱帧间的连续性与其频谱重建的准确性具有同样的感知重要性.本文选择DLSD作为动态失真测度来评价扩展后音频信号频谱包络的时间演变平滑程度.如果DLSD值较小，则可认为音频频谱在时间上变化相对缓慢，有益于重建音频的整体主观听觉质量.DLSD测度[24]可定义如下，

dDLSD(i)=

(17)

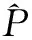
表8同样给出了两种方法重建音频DLSD的结果.其中，小提琴独奏、交响乐音频高频成分能量较低，同时高频频谱的时间平滑性较好，因此两种扩展方法重建音频的动态失真差异并不大.而ESN方法对爵士、摇滚、乡村音乐中暂态成分的刻画更接近于原始音频，其DLSD数值明显优于GMM方法.对于语音，ESN方法DLSD分数在3.40dB左右，较GMM提升了0.7dB左右.

综上所述，在静态失真方面本文所提出的ESN方法平均性能相比GMM参考算法略有提升；而除交响乐音频外，ESN方法所重建大部分音频的动态失真均优于参考算法.

4.4 主观偏爱测试

本文采用主观偏爱测试的方法来评价不同扩展方法的主观质量.测试过程中邀请了20名年龄在22～28岁的被测者来选择两种被测项中较为偏爱的一种，或者选择无偏爱.主观测试安排在静音室中，并选择了MPEG音频数据库中的五句作为测试数据(其中包括乡村音乐、爵士音乐、摇滚音乐、小提琴独奏、交响乐各一句).测试音频的顺序采用随机排列的方式.被测者在做出判断之前可随意重复监听测试数据.

本次主观测试分为三组：ESN方法与GMM方法比较、ESN方法与原始超宽带音频比较、原始超宽带音频与GMM方法比较.最终的主观测试结果如表9所示.结果可以看出，本文所提ESN方法扩展后的音频主观质量比GMM方法更接近于原始超宽带音频质量.尽管ESN方法重建交响乐音频的客观质量不及参考算法重建音频，但是由于交响乐音频高频能量较为暗淡，两种扩展方法重建音频的主观质量差异并不明显.

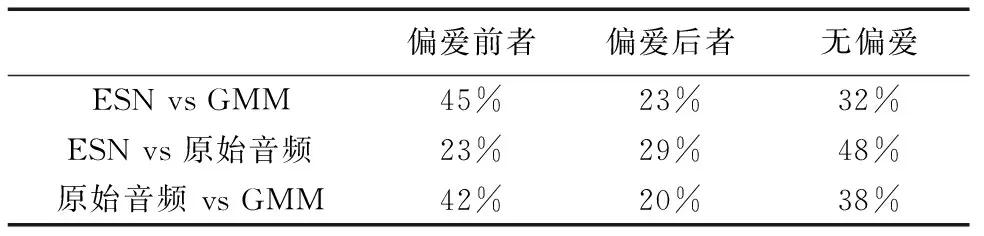
表9 主观偏爱测试结果

4.5 计算复杂度

此外，本文分别对所提方法和参考方法每帧内需要乘法计算的次数进行了统计.两种方法在特征提取、时频变换、频带复制以及高频成分重建等模块的计算过程完全一致，因此可只针对频谱包络估计模块进行复杂度计算.对于ESN方法，其每帧需要进行245364次乘法运算；而GMM方法则需要进行256512次乘法运算.由此可见，ESN方法计算复杂度略低于参考算法.

4.6 讨论

本文所提出的ESN方法利用储备池中的递归结构，将音频特征空间的动态演变过程引入到高频频谱包络估计方法中，在不增加计算复杂度的前提下降低了扩展后音频的静态和动态失真.然而，神经网络的参数训练与样本数据的分布特性直接相关.如果输入宽带音频包含噪声和混响成分，本文所提方法扩展后音频的主客观质量也会出现一定的降低.在未来工作中，可以考虑将音频增强和频带扩展相结合，改善ESN网络在含噪情况下的鲁棒性，进而提升整体算法的实用性.

5 结束语

本文提出了一种基于ESN的音频频带扩展方法.该方法借助ESN储备池中的递归结构描述了特征空间状态的动态更新，并依据线性观测方程对高低频特征参数间的映射关系进行拟合，实现了高频频谱包络的有效估计.主客观测试结果表明，对于多数测试数据，ESN方法相比于GMM参考方法在静态和动态失真方面均获得了提升，其重建音频更接近于原始超宽带音频的听觉质量.

[1]VARY P,MARTIN R.DigitalSpeech Transmission-Enhancement,Coding and Error Concealment[M].UK:John Wiley & Sons Ltd,2006.

[2]LARSEN E,AARTS R M.AudioBandwidth Extension-Application of Psychoacoustics,Signal Processing and Loudspeaker Design[M].UK:John Wiley & Sons Ltd,2004.

[4]CHENG Y M,O'SHAUGHNESSY D,MERMELSTEIN P.Statistical recovery of wideband speech from narrowband speech[J].IEEE Transactions on Speech and Audio Processing,1994,2(4):544-548.

[5]CARL H,HEUTE U.Bandwidth enhancement of narrow-band speech signals[A].7th European Signal Processing Conference (EUSIPCO)[C].Edinburgh,Scotland:EURASIP,1994.1178-1181.

[6]EPPS J,HOLMES W H.A new technique for wideband enhancement of coded narrowband speech[A].IEEE Workshop on Speech Coding Proceedings[C].Porvoo:IEEE,1999.174-176.

[7]SOON I Y,CHAI K Y.Bandwidth extension of narrowband speech using soft-decision vector quantization[A].Fifth International Conference on Information,Communications and Signal Processing[C].Bangkok:IEEE,2005.734-738.

[8]KORNAGEL U.Techniques for artificial bandwidth extension of telephone speech[J].Signal Processing,2006,86(6):1296-1306.

[9]PARK KY,KIM HS.Narrowband to wideband conversion of speech using GMM based transformation[A].IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP)[C].ISTANBUL:IEEE,TURKEY,2000.1843-1846.

[10]BOTINHAO CV,CARLOS BS,CALOBA LP,PETRAGLIA MR.Frequency extension of telephone narrowband speech signal using neural networks[A].IMACS Multiconference on Computational Engineering in Systems Applications (CESA)[C].Beijing:IEEE,2006.1576-1579.

[11]TUAN V P,SCHAEFER F,KUBIN G.A novel implementation of the spectral shaping approach for artificial bandwidth extension[A].3rd International Conference on Communications and Electronic[C].Nha Trang,VIETNAM:IEEE,2010.262-267.

[12]ISER B,SCHMIDT G.Neural networks versus codebooks in an application for bandwidth extension of speech signals[A].European Conference on Speech and Language Processing (EUROSPEECH)[C].Geneva,Switzerland:ISCA,2003.565-568.

[13]JAX P,VARY P.Wideband extension of telephone speech using a hidden Markov model[A].7th IEEE Workshop on Speech Coding[C].DELAVAN,WI:IEEE,2000.133-135.

[14]JAX P,VARY P.On artificial bandwidth extension of telephone speech[J].Signal Processing,2003,83(8):1707-1719.

[15]SONG G B,MARTYNOVICH P.A study of HMM-based bandwidth extension of speech signals[J].Signal Processing,2009,89(10):2036-2044.

[16]YAGLI C,TURAN M A T,ERZIN E.Artificial bandwidth extension of spectral envelope along a Viterbi path[J].Speech Communication,2013,55(1):111-118.

[17]LUKOEVIIUS M.APractical Guide to Applying Echo State Networks[M].MONTAVON G,ORR G B,MLLER K R.Neural Networks:Tricks of the Trade,Heidelberg:Springer,2012.659-686.

[18]LUKOSEVICIUS M,JAEGER H.Reservoir computing approaches to recurrent neural network training[J].Computer Science Review,2009,3(3):127-149.

[19]JAEGER H,LUKOSEVICIUS M,POPOVICI D,SIEWERT U.Optimization and applications of echo state networks with leaky-integrator neurons[J].Neural Networks,2007,20(3):335-352.

[20]JAEGER H,HAAS H.Harnessing nonlinearity:predicting chaotic systems and saving energy in wireless communication[J].Science,2004,304(5667):78-80.

[21]SCHILLER U D,STEIL JJ.Analyzing the weight dynamics of recurrent learning algorithm[J].Neucomputing,2005,(63):757-779.

[22]PULAKKA H,LAAKSONEN L,VAINIO M,POHJALAINEN J,ALKU P.Evaluation of an artificial speech bandwidth extension method in three languages[J].IEEE Transactions on Audio,Speech,and Language Processing,2008,16(6):1124-1137.

[23]GRAY A H,MARKEL J D.Distance measures for speech processing[J].IEEE Transactions on Audio,Speech,and Language Processing,1976,24(5):380-391.

[24]NORDEN F,ERIKSSON T.Time evolution in LPC spectrum coding[J].IEEE Transactions on Speech and Audio Processing,2004,12(3):290-301.

[25]NILSSON M,GUSTAFSSON H,ANDERSEN SV,KLEIJN W B.Gaussian mixture model based mutual information estimation between frequency bands in speech[A].IEEE International Conference on Acoustics,Speech,and Signal Processing (ICASSP)[C].Orlando,Florida:IEEE,2002.I-525-528

刘 鑫 男,1986年生于北京.北京工业大学博士研究生.研究方向为语音与音频信号处理.

鲍长春(通信作者) 男,1965年生于内蒙古赤峰.北京工业大学电子信息与控制工程学院教授,博士生导师.研究方向为语音与音频信号处理.

E-mail:chchbao@bjut.edu.cn

Audio Bandwidth Extension Method Based on Echo State Network

LIU Xin,BAO Chang-chun

(SchoolofElectronicInformationandControlEngineering,BeijingUniversityofTechnology.Beijing100124,China)

The bandwidth limitation in wideband audio communication systems degrades the subjective quality and naturalness of the reproduced signals.In this paper,a wideband to super-wideband audio bandwidth extension method was proposed by using echo state network.The echo state network is adopted to model the mapping function between the low-and high-frequency spectral coefficients of audio signals,and the temporal evolution of audio features is represented by continuously state updating on the basis of the recursive structure in the network,for effectively estimating the high-frequency spectral envelope.By combining the high-frequency fine spectrum extended by spectral translation,the proposed method can effectively extend the bandwidth of wideband audio to super-wideband.Evaluation results show that the proposed method upgrades the auditory quality of wideband audio,and gains better extension performance than the Gaussian mixture model-based bandwidth extension method in terms of both static and dynamic distortions for most test data.

audio coding;audio bandwidth extension;echo state network;spectral translation

2015-06-15;

2015-11-15;责任编辑：蓝红杰

国家自然科学基金(No.61072089，No.61471014)

TN912.3

A

0372-2112 (2016)11-2758-09

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.11.027