一种基于随机投影的贝叶斯时间差分算法

刘 全,于 俊,王 辉，傅启明,朱 斐

(1.苏州大学计算机科学与技术学院,江苏苏州 215006;2.吉林大学符号计算与知识工程教育部重点实验室,吉林长春 130012：3.软件新技术与产业化协同创新中心，江苏南京 210023)



一种基于随机投影的贝叶斯时间差分算法

刘 全1,2，3,于 俊1，3,王 辉1，3，傅启明1，3,朱 斐1，3

(1.苏州大学计算机科学与技术学院,江苏苏州 215006;2.吉林大学符号计算与知识工程教育部重点实验室,吉林长春 130012：3.软件新技术与产业化协同创新中心，江苏南京 210023)

在强化学习方法中,大部分的算法都是基于值函数评估的算法.高斯过程时间差分算法利用贝叶斯方法来评估值函数,通过贝尔曼公式和贝叶斯规则,建立立即奖赏与值函数之间的概率生成模型.在状态空间中,通过在线核稀疏化并利用最小二乘方法来求解新样本的近似线性逼近,以提高算法的执行速度,但时间复杂度依然较高.针对在状态空间中近似状态的选择问题,在高斯过程框架下提出一种基于随机投影的贝叶斯时间差分算法,该算法利用哈希函数把字典状态集合中的元素映射成哈希值,根据哈希值进行分组,进而减少状态之间的比较.实验结果表明,该方法不仅能够提高算法的执行速度,而且较好地平衡了评估状态值函数精度和算法执行时间.

强化学习;马尔科夫决策过程;高斯过程;随机投影;时间差分算法

1 引言

强化学习(Reinforcement Learning,RL)是在未知、动态环境中在线求解最优策略,以获取最大期望回报的一类算法.强化学习方法的基本框架为:Agent通过试错与环境进行交互,将每一步的延迟回报通过时间信用分配机制传递给过去动作序列中的某些动作,用值函数评价每个状态或状态动作对的好坏程度,最终通过值函数确定最优策略[1,2].目前强化学习方法越来越多地被用于在线控制、作业调度、游戏等领域[3,4].

马尔科夫决策过程(Markov Decision Process,MDP)是一类重要的随机过程,经常用来对强化学习进行建模[5].Sutton在1998年提出对马尔科夫链学习的理论和TD(λ)算法[6].核方法在监督学习和无监督学习问题中都得到了广泛的研究[7].目前基于核的强化学习理论与应用成果还较少,这主要是由于核方法需要随机或重复的获取训练样本[8].直到2002年,Ormoneit 等人提出了基于核的强化学习方法[9].后来,Xu等人提出了基于核的最小二乘TD方法(Kernel-based Least Squares TD,KLSTD),将基于核的逼近与LSTD相结合[10],取得了一定的效果.在KLSTD基础之上,Xu等人继续提出了KLSPI及KLSPI-Q算法[11],并证明了方法的有效性.Yaakov Engel等人提出了一种新的值函数评估方法,该方法利用核方法来估计值函数,选择核方法中的高斯过程 (Gaussian process)模型[12]为值函数建模,通过高斯过程与时间差分方法相结合得到高斯过程的时间差分(Gaussian Process Temporal Difference,GPTD)学习算法[13，14],建立值函数的概率生成模型,然后根据先验,以及观测到的样本,利用贝叶斯推理得到值函数完整的后验分布.

对于固定的策略,GPTD能够较准确的评估该策略的值函数,但是GPTD算法的明显缺点是模型的学习完全依赖于样本,计算量较大.Engel等人提出了依赖于特征空间的在线核稀疏化方法,将核函数看作是在高维希伯尔特空间上的两个向量的内积,直接去除那些能够用特征空间中特征近似线性逼近的样本[15],利用最小二乘方法来求解新样本的近似线性逼近,以提高时间和空间效率.

本文针对在强化学习状态空间中需要选择近似状态的问题,在高斯过程框架上提出一种基于随机投影的贝叶斯时间差分算法(Bayesian Temporal Difference algorithm based on Random Projection,RPGPTD).该算法对于新状态,首先进行预处理,把状态转变为二进制编码,使得相似的数据对象,其二进制编码也相似,在此基础上进行相似性比较选择,同时设置参数阈值来控制状态字典集合逼近真实状态空间程度.实验结果表明,该方法不仅能够提高算法的执行速度,而且在值函数评估质量和时间上有较好的平衡.

2 相关理论

2.1 马尔科夫决策过程

在强化学习中,通常用马尔科夫决策过程来对描述的问题进行建模,它把强化学习问题描述为一个四元组M=,其中X是环境的状态集合;U是Agent能采取的动作集合;f(·|x,u)为状态x下执行动作u转移到下一状态的概率分布,它对后继状态的不确定性进行了模型化;f0(·)表示初始状态被选择的概率分布;ρ(·|x,u)是立即奖赏函数的概率分布,r(x,u)是满足ρ(·|x,u)的一个随机变量,表示在状态x处,Agent执行动作u,到达后继状态x′获得的奖赏值.

强化学习中,值函数通常分为两种:状态值函数和动作值函数.本文以状态值函数为基础,但是很容易扩展到动作值函数,状态值函数V(x)是指当前状态x下回报R(x)的期望值.

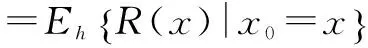
=Eh{r(x)+γR(x′)}

(1)

2.2 高斯过程时间差分算法

(2)

将公式(2)带入公式(1)中,可得到关于立即奖赏的生成模型,如公式(3)所示.

r(x)=V(x)-γEx′|x{V(x′)}+N(x)

(3)

在确定性问题的在线学习过程中,公式(3)可以改写成公式(4).

r(x)=V(x)-γV(x′)+N(x)

(4)

其中,N(x)为噪声项.

假定给定一条包含t+1个样本的路径ξ=(x0,x1,…,xt-1,xt),可以得到如公式(5)所示的t个等式.

r(xi)=V(xi)-γV(xi+1)+N(xi)

(5)

将这t个等式的状态值函数、立即奖赏以及噪声分别写成向量的形式,如公式(6)、(7)、(8)所示.

Vt=(V(x0),V(x1),…,V(xt))T

(6)

rt-1=(r(x0),r(x1),…,r(xt-1))T

(7)

Nt-1=(N(x0),N(x1),…,N(xt-1))T

(8)

根据这组样本序列及公式(5),可得一个包含t个等式的向量表达式,如公式(9)所示.

rt-1=HtVt+Nt-1

(9)

其中,Ht是一个t×(t+1)的矩阵,如公式(10)所示.

(10)

类比于高斯过程回归方法,高斯过程时间差分算法在值函数上引入高斯先验,即V～N(0,k(·,·)),意味着V是一个高斯过程,对于所有的x,x′∈X都有先验E(V(x))=0和E(V(x)V(x′))=k(x,x′),为了使得k(·,·)是一个合理的协方差函数,需要核函数是对称正定的,且核函数的选择需要反映出两个状态之间的先验关系.因此,Vt～N(0,Kt),其中[Kt]i,j=k(xi,xj).

假设1 假设各状态的立即奖赏的噪声项相互独立服从于高斯分布且与状态值函数V相互独立,均值为0,方差为σ2(x),即:N(x)～N(0,σ2(x)).则噪声向量Nt-1的分布形式如公式(11)所示.

(11)

(12)

(13)

假设变量X和变量Y是随机向量,且满足多元正态分布,即

利用贝叶斯规则,则变量X的后验X|Y满足公式(14)

(14)

由此可以得出,设在一个情节中,前t个时刻,有样本路径ξ=(x0,x1,…,xt-1),以及奖赏序列rt-1=(r(x0),r(x1),…,r(xt-1))T.

3 基于随机投影的贝叶斯差分算法及分析

3.1 稀疏化方法

(15)

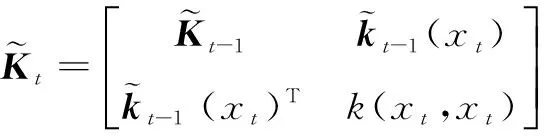
(16)

(17)

(18)

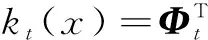
(19)

由公式(18)、(19)可得到稀疏化后的状态值函数的后验,如公式(20)所示:

(20)

3.2 基于随机投影的贝叶斯时间差分算法

定义1 对于状态集合X,集合内的状态间相似度的计算公式为sim(·,·),如果存在一个哈希函数hash(·)满足以下条件:存在一个相似度s到概率p的单调递增映射关系,使得X中的任意两个元素a和b满足sim(a,b)≥s,且hash(a)=hash(b)的概率大于p,那么hash(·)就是该集合的一个随机投影哈希函数.

随机投影方法主要分为预处理阶段和选择阶段两个部分.

(21)

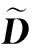
(22)

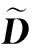
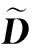
在强化学习中,对于情节式任务,设最后一个状态为bound(vt)∈[-0.07,+0.07],由于bound(pt)∈[-1.2,+0.5],因此对于样本g,有以下公式:

g=-0.0025

(23)

即,可以暂时先把折扣因子置为0,遇到非终止状态时再把折扣因子重置为初始值.

下面给出基于随机投影的贝叶斯时间差分算法.

4 实验及结果分析

为了验证随机投影高斯过程时间差分算法的有效性,以经典的离散状态空间的格子世界为基础平台,来对RPGPTD算法的性能进行测评,并通过与已有的GPTD算法进行性能对比来说明RPGPTD算法的优越性.

在一个9×9的格子世界,每个格子代表一个状态,每个状态可采取的动作包括上、下、左、右4个方向的运动.每次状态迁移时,Agent得到的立即奖赏均为-1,到达终止状态时的奖赏也为-1.折扣因子γ=1.

阈值取为ν=1,所有噪声方差均取σ2=0.1.

在遵循策略h的情况下,分别对RPGPTD算法与GPTD算法执行1000个情节,比较两个算法的执行时间和值函数估计误差.在给定算法参数后,每个算法都独立运行10次,每次独立运行都计算出两种算法所需的时间以及对所有状态进行值函数估计的均方误差,然后再计算各次独立运行的所需时间和值函数估计均方误差的平均值,以此来作为算法的评价指标.

首先,考察RPGPTD算法与GPTD算法在格子世界中执行500以及1000个情节所需的时间,其中RPGPTD算法的参数l分别取为2,4,8,10,时间的单位为秒(s),如表1所示.

表1 9×9格子世界问题RPGPTD算法与GPTD算法在一定情节数内执行算法的时间比较

9×9格子世界问题500episodes1000episodesGPTD算法634.616s1362.522sRPGPTD算法l=2518.705s1079.906sRPGPTD算法l=4474.883s959.941sRPGPTD算法l=8480.905s953.443sRPGPTD算法l=10494.030s975.366s

针对RPGPTD算法,在减少算法执行时间的基础上,进一步对值函数评估的准确度进行考察.利用动态规划方法(DP)迭代可以计算出准确的状态值函数,动态规划更新公式为:

(24)

将RPGPTD算法与GPTD算法执行1000个情节得到的状态值函数与利用动态规划方法得到的值函数进行比较.以均方根误差函数作为比较准则:

(25)

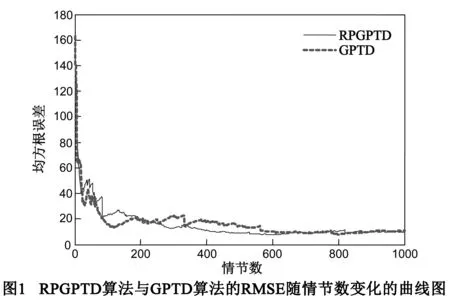
图1给出了RPGPTD算法与GPTD算法的状态值函数的均方根误差随情节数增加而变化的曲线图.图中RPGPTD算法的参数l取为2.由图可以看出,在遵循策略h的情况下,RPGPTD算法与GPTD算法对状态值函数的评估能力一致,两种算法在200个情节数后都能很好的收敛,且逼近精度也一致.

下面探究RPGPTD算法中参数l对值函数评估的影响,图2所示的曲线是参数l分别取为2,4,8,10时RMSE随情节数的变化图.当参数l取2,4时,在前200个情节,RMSE的值震荡下降,震荡较大,200个情节之后震荡较小,逐渐趋于一致且收敛,当参数l取8,10时,在前200个情节,RMSE震荡较大,但是在200个情节后,RMSE曲线图明显高于参数取2,4时的曲线图,即对状态值函数的评估误差较大,评估结果不理想,所以在参数l较大时,状态值函数评估误差较大.由此可见,理想情况下,参数l越大,执行速度越快,并且呈指数级的提升,但是,在这种情况下哈希函数HASH(·)的概率公式p(s)可以表示为与新来状态x的相似度为s的状态的召回率.当参数l的取值越大时状态的召回率必然降低,所以RPGPTD算法在参数l增大时,对状态值函数的评估效果不理想.

5 结论

本文针对于在强化学习状态空间中近似状态的选择问题,基于高斯过程时间差分框架,提出一种基于随机投影的贝叶斯时间差分算法.高斯过程时间差分算法通过贝尔曼公式和贝叶斯规则,建立立即奖赏与值函数之间的概率生成模型,但在评估值函数时,算法执行速度较慢,为进一步提升执行时间,利用哈希函数把字典状态集合中的元素映射成哈希值,把状态转变为二进制编码,使得相似的数据对象,其二进制编码也相似,根据哈希值进行分组,进而减少状态之间的比较,同时设置参数阈值来控制状态字典集合逼近真实状态空间的程度.实验结果表明,该方法不仅能够提高算法的执行速度,而且在评估状态值函数精度和算法执行时间上有较好的平衡.

[1]Sutton R S,Barto A G.Reinforcement Learning:An Introduction[M].Cambridge:MIT Press,1998.

[2]傅启明,刘全,尤树华,黄蔚,章晓芳.一种新的基于值函数迁移的快速Sarsa算法[J].电子学报,2014,42(11):2157-2161.

Fu Qiming,Liu Quan,You Shuhua,Huang Wei,Zhang Xiaofang.A novel fast Sarsa algorithm based on value function transfer[J].Acta Electronica Sinica,2014,42(11):2157-2161.(in Chinese)

[3]Martínez Y,Nowé A,Suárez J,et al.A Reinforcement Learning Approach for the Flexible Job Shop Scheduling Problem[M].Learning and Intelligent Optimization:Springer Berlin Heidelberg,2014.253-262.

[4]Amato C,Shani G.High-level reinforcement learning in strategy games[A].Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems[C].International Foundation for Autonomous Agents and Multiagent Systems,2010.75-82.

[5]Marco Wiering,Martijn van Otterlo.Reinforcement Learning State of the Art[M].Singapore:Springer Press,2012.

[6]Sutton R S.Learning to predict by the methods of temporal differences[J].Machine Learning,1988,3(1):9-44.

[7]Shawe-Taylor J,Cristianini N.Kernel Methods for Pattern Analysis[M].Cambridge:Cambridge University Press,2004.

[8]Scholkopf B,Smola A J.Learning with Kernels:Support Vector Machines,Regularization,Optimization,and Eyond[M].Cambridge:MIT Press,2002.

[9]Ormoneit D,Sen.Kernel-based reinforcement learning[J].Machine Learning,2012,49(2-3):161-178.

[10]Xu X,Xie T,Hu D,et al.Kernel least-squares temporal difference learning[J].International Journal of Information Technology,2005,11(9):54-63.

[11]Xu X,Hu D,Lu X.Kernel-based least squares policy iteration for reinforcement learning[J].IEEE Transactions on Neural Networks,2007,18:973-992.

[12]C E Rasmussen and C K I Williams.Gaussian Processes for Machine Learning[M].Cambridge:MIT Press,2006.

[13]Engel Y,Mannor S,Meir R.Bayes meets Bellman:the gaussian process approach to temporal difference learning[A].Proceedings of the 20th International Conference on Machine Learning[C].Washington:AAAI,2011.154-161.

[14]Engel Y,Mannor S,Meir R.Reinforcement learning with gaussian processes[A].Proceedings of the 22nd International Conference on Machine Learning[C].Bonn:ACM,2014.201-208.

[15]Engel Y,Mannor S,Meir R.Sparse Online Greedy Support Vector Regression[M].Berlin:Springer,2002.

刘 全 男,1969年生于内蒙古,博士,教授,博士生导师.主要研究方向为强化学习、无线传感器网络、智能信息处理.

E-mail:quanliu@suda.edu.cn

于 俊 男，1989年生于江苏泰州，硕士.主要研究方向为强化学习、贝叶斯推理.

A Bayesian Temporal Difference Algorithm Based on Random Projection

LIU Quan1, 2, 3,YU Jun1,3,WANG Hui1,3,FU Qi-ming1,3, ZHU Fei1,3

(1.SchoolofComputerScienceandTechnology,SoochowUniversity,Suzhou,Jiangsu215006,China;2.KeyLaboratoryofSymbolicComputationandKnowledgeEngineeringofJilinUniversity,MinistryofEducation,JilinUniversity,Changchun,Jilin130012,China；3.CollaborativeInnovationCenterofNovelSoftwareTechnologyandIndustrialization，Nanjing,Jiangsu210023,China)

Most algorithms are based on policy evaluation in reinforcement learning.The Gaussian process temporal difference is an algorithm that uses Bayesian solution to evaluate value functions.In the method,Gaussian process builds a probabilistic generative model between the immediate reward and the value function through Bellman Equation and Bayesian rule.In order to improve the efficiency of the algorithm,approximate linear approximation for new samples is solved by on-line kernel sparse and least squares in state space.However,the time complexity is still high.To deal with this problem,a Bayesian temporal difference algorithm bases on random projection algorithm is proposed.The elements in dictionary state set are mapped to hash values by hash function.According to the hash values,groups are divided and the comparison between the states is reduced.The experimental results show that this algorithm not only improves the execution speed,but also obtains balance between execution time and precision of the state value function.

reinforcement learning;markov decision process;gaussian process;random projection;temporal difference learning

2015-04-08;

2015-08-17;责任编辑:蓝红杰

国家自然科学基金(No.61272005,No.61303108,No.61373094,No.61472262，No.61502323，No.61502329);江苏省自然科学基金(No.BK2012616)；江苏省高校自然科学研究项目(No.13KJB520020);吉林大学符号计算与知识工程教育部重点实验室项目(No.93K172014K04);苏州市应用基础研究计划工业部分(No.SYG201422，No.SY201308)

TP181

A

0372-2112 (2016)11-2752-06

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.11.026