一致可微T函数性质研究

王森鹏,刘 燕,胡 斌

(解放军信息工程大学,河南郑州 450001)



一致可微T函数性质研究

王森鹏,刘 燕,胡 斌

(解放军信息工程大学,河南郑州 450001)

本文结合传统T函数理论与非阿基米德T函数理论,深入研究T函数的性质特点,重点讨论一致可微T函数的单圈性及最高位序列的保熵性.首次利用参数的概念建立传统T函数理论中单字T函数单圈性判定条件与非阿基米德T函数理论中单圈性判定条件的联系,说明了两类判定条件的适用范围.定义了对T函数生成序列进行压缩变换的保熵性概念,讨论了一致可微T函数最高位序列的保熵性,说明了一致可微的T函数保熵性具有传递性,给出了T函数最高位序列保熵性的判定条件.

T函数;一致可微;参数;保熵性

1 引言

T函数是2002年由Klimov和Shamir在文献[1]中提出的一类非线性函数.由于具有计算速度快、密码学性质好、易于软硬件实现等特点,T函数被广泛应用于序列密码、分组密码等领域.特别是在流密码设计中,T函数能代替线性移位寄存器(LFSR)作为初始乱源,从而克服了LFSR生成序列周期无法达到最大的缺陷.Klimov和Shamir在文献[1～3]中利用参数的概念给出了T函数单圈性的判定条件,并提出基于T函数的流密码设计方案.2004后,大量基于T函数设计的密码算法开始涌现,如eSTREAM计划中提交的TSC[4],ABC[5],Mir[6]等密码算法均采用T函数,同时针对这些算法的攻击方法也成为研究的热点.文献[7～10]对T函数输出序列的密码学性质进行了深入研究,包括线性复杂度、k-错线性复杂度、自相关性和非线性度等安全性指标,研究表明T函数具有较好的安全性.

研究T函数的另一重要途径是非阿基米德理论,Anashin在2-adic整数环中,定义了2-adic距离、范数、测度等概念,阐述了T函数即1-Lipchis函数(或称为完备函数),而可逆T函数即可测函数,单圈T函数即保测函数[11].同时,分别利用一致可微性、马勒插值级数和van der put级数,给出了可逆T函数以及单圈T函数的的判定定理[12～15].2012年,Tao Shi,Anashin和DongDai Lin等人在该理论的基础上,发现一致可微T函数的特定分位序列之间存在线性弱点,并提出攻击方法[16].2013年,他们又利用van der put级数作为工具,借鉴时间存储折中的思想提出了两类快速计算T函数的算法[17].

近年来,在T函数的单圈性判定方面,传统T函数理论与非阿基米德理论均取得了丰富的成果,其中传统理论主要是利用参数作为工具对T函数进行研究,而非阿基米德理论则是借助T函数一致可微的性质进行研究,两种理论各有特点、各有优势.如果能将两种理论结合起来对T函数的性质进行研究是非常有意义的,本文从这方面出发建立起两种理论之间的联系,为T函数的研究提供了新的思路.

2 基础知识

首先,给出传统意义下T函数的相关定义:

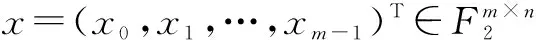
本文的研究重点为单字T函数,故下文在不加说明的情况下,T函数均指单字T函数.

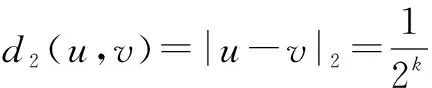
另外,距离度量满足强三角不等式:任意a,b∈Z2,有|a+b|2≤max{|a|2,|b|2},满足这一特性的度量又被称为超度量空间或非阿基米德度量空间.在该度量空间中,可以讨论可微性,可导性,连续性,极限等性质.此时,可以利用度量的概念给出1-Lipschitz函数的定义,即为单字T函数的定义.

定义5[11]若Z2→Z2上的函数f(x)对于任意u,v∈Z2,都有|f(u)-f(v)|2≤|u-v|2成立,则称f(x)为2-adic整数环上的1-Lipschitz函数.

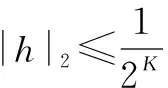
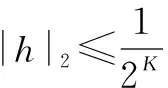
f(x+h)≡f(x)+f′(x)·h(mod2ord2h+M)

具有上述特性的K=K(M)的最小值记为NM(f).

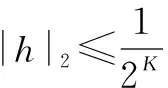
f(x+h)≡f(x)+f′(x)·h(mod2ord2h+M)

给定M,具有上述特性的K=K(M)的最小值记为NM(f),这里NM(f)的含义与定义7中的一致.

3 参数与一致可微

下面利用非阿基米德理论,对传统T函数中的参数概念进行深入研究,建立起非阿基米德理论中单圈性判定条件与传统T函数理论中单圈性判定条件之间的联系,首先,给出相关引理.

引理1[11]设f:Z2→Z2是模2一致可微T函数,则其是可逆的当且仅当f模2NM(f)+1是可逆的.

引理2[11]设f:Z2→Z2是模4一致可微T函数,则其是单圈的当且仅当f模2NM(f)+2是单圈的.

引理3[11]设f:Z2→Z2是模4一致可微单圈T函数,则对任意x∈Z2,其导数满足f′(x)≡1(mod2).

上述引理中,引理2基于非阿基米德理论给出了判定一类T函数是否为单圈T函数的方法,引理6基于传统T函数理论给出了判定所有T函数是否为单圈T函数的方法.引理2的条件易于判定,但只对特殊的T函数成立;引理6的判定条件对所有的T函数成立,但考查其充要条件存在一定的困难.所以为了寻找更好的判定方法,我们通过研究传统理论中参数的概念在非阿基米德理论中的含义,找出不同判定条件之间的联系,给出不同判定条件的适用范围.

定理1 T函数f(x)为Z2→Z2上的参数当且仅当f(x)模2一致可微,且对任意x∈Z2,满足f′(x)≡0(mod2).

证明 充分性:由于f(x)模2一致可微,则存在正整数K,使得当|h|2≤2-K(即h≡0mod2K)时,对任意x∈Z2,满足f(x+h)≡f(x)+f′(x)·h(mod2ord2h+1),又因为对任意x∈Z2,有f′(x)≡0(mod2),则当k≥K时,令h=2k,得到f(x+2k)≡f(x)(mod2k+1),根据参数的定义知f(x)为参数.

必要性:由于f(x)为参数,则存在整数K,当k≥K时,有f(x+2k)≡f(x)(mod2k+1)成立,即对任意h≡0mod2K,有f(x+h)≡f(x)+0×h(mod2k+1)成立.则由一致可微的定义得,f为模2一致可微的,且对任意x∈Z2,f′(x)≡0(mod2).

定理1给出了参数在非阿基米德理论中的描述,建立了两种理论之间的联系,在此基础上,我们将讨论奇参数与偶参数的性质,并给出它们在非阿基米德理论中的描述.

定理2 若f:Z2→Z2是模4一致可微T函数,且对任意x∈Z2,有f′(x)≡0(mod2)成立,则当k≥N2(f)+2时,f为偶参数.

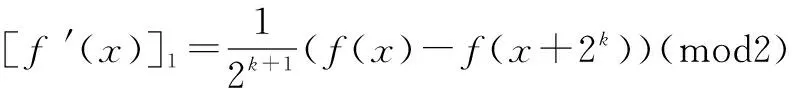
由偶参数的定义得,当k≥N2(f)+2时,f为偶参数.

推论1 若T函数f:Z2→Z2为奇参数,则f一定不是模4一致可微的.

定理1和定理2说明模4一致可微的参数一定是偶参数,但偶参数不一定是模4一致可微的.推论1表明奇参数一定不是模4一致可微的,根据奇偶参数与一致可微性的关系,结合单圈T函数的判定定理,得到以下结论:

推论2 若存在正整数K,使得T函数g(x)=x+f(x)mod2K为单圈函数,则g(x)是单圈T函数当且仅当f(x)是模4一致可微的,且对任意x∈Z2,有f′(x)≡0(mod2),同时满足N2(f)≤K.

定理3 若单圈T函数f(x):Z2→Z2是模4一致可微的,则f(x)可以表示成f(x)=x+r(x)的形式,其中当k≥N2(f)+2时,r(x)为偶参数.

证明 由于单圈T函数f(x):Z2→Z2是模4一致可微的,由引理3得f′(x)≡1(mod2),且当|h|2≤2-N2(f)时,对任意x∈Z2,下式成立:

f(x+h)≡f(x)+f′(x)·h(mod2ord2h+2)

令r(x)=f(x)-x,任取|h|2≤2-N2(f)(即h≡0mod2N2(f)),对任意x∈Z2,有:

r(x+h)≡f(x+h)-(x+h)≡f(x)+h·f′(x)-(x+h)

≡r(x)+h·(f′(x)-1)≡r(x)+h·r′(x)(mod2ord2h+2)

由f′(x)≡1(mod2),得到r′(x)≡0(mod2),且由一致可微的定义知r(x)为模4一致可微的.根据定理2,则当k≥N2(f)+2时,r(x)为偶参数,得证.

定理1、定理2及推论1描述了传统T函数理论中参数、奇参数和偶参数等概念与非阿基米德理论中一致可微性的关系,说明了参数均是模2一致可微的、模4一致可微的参数一定是偶参数、奇参数一定不具有模4一致可微性,这为进一步研究T函数的性质提供了理论支撑.同时,结合已有的T函数单圈性判定方法,发现非阿基米德理论中利用一致可微性判定T函数单圈性的方法,部分适用于传统理论中通过偶参数构造的T函数,而对基于奇参数构造的T函数,该判定方法不再适用,这为研究T函数的判定方法提供了新的工具.

4 T函数最高分位序列保熵性研究

由于T函数第i路输出只与第0,…,i路输入有关,因此T函数所有输出分位序列中最高分位序列包含的输入信息最多.本节考察单圈T函数输出的最高分位序列是否具有保熵性.

根据T函数的构造方法和结构特点,不难发现任意单圈T函数输出序列的最高分位序列可由多个不同的单圈T函数生成,故任意单圈T函数输出序列的最高分位序列不具有保熵性.因此,我们将考察的范围限制到具有某一特性的单圈T函数.

引理7[15]设f(x):Z2→Z2是模4一致可微的T函数,则其导数模4是周期函数,且周期是2N2(f)的因子,即per{f′(x)(mod4)}|2N2(f).

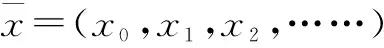
xi+2j-1,j=xi,j⨁x2j-1,j⨁xi,j-1⨁x0,j⨁x0,j-1⨁y(i)(mod2)

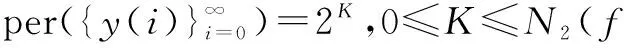
从引理8的证明过程中,可以得到以下结论:

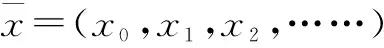
xi+2j-1,j=xi,j⨁xk+2j-1,j⨁xi,j-1⨁xk,j⨁xk,j-1⨁y(i)(mod2)

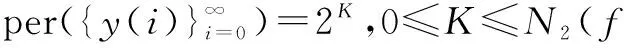
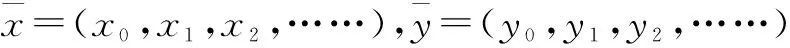
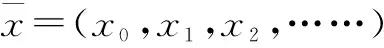
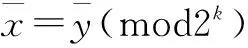
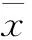
xi+2k-2,k-1=xi,k-1⨁xt+2k-2,k-1⨁xi,k-2

⨁xt,k-1⨁xt,k-2⨁α(i)(mod2)

yi+2k-2,k-1=yi,k-1⨁yt+2k-2,k-1⨁yi,k-2

⨁yt,k-1⨁yt,k-2⨁β(i)(mod2)

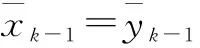
进一步地,当n=k+1时,任意时刻i由推论3,有

xi+2k-1,k=xi,k⨁xt+2k-1,k⨁xi,k-1⨁xt,k

⨁xt,k-1⨁α(i)(mod2)

=yi+2k-1,k=yi,k⨁yt+2k-1,k⨁yi,k-1⨁yt,k

⨁yt,k-1⨁β(i)(mod2)

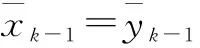
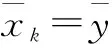
xi+2k-1+1=f(xi+2k-1)=f(xi+(xi+2k-1-xi))

=f(xi)+(xi+2k-1-xi)f′(xi)(mod2k)

yi+2k-1+1=g(yi+2k-1)=g(yi+(yi+2k-1-yi))

=g(yi)+(yi+2k-1-yi)g′(yi)(mod2k)

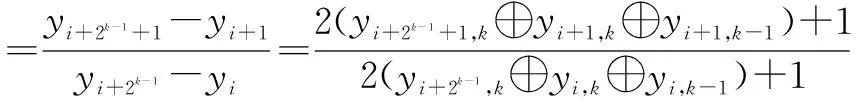
定理4说明对于一类模4一致可微且具有相似结构(即相近的N2(f)值)的单圈T函数,考察其中任意两个不同的T函数能否生成相同的最高分位输出序列只需考察当输入规模较小时(n=N2(f)+2),结论是否成立.

5 小结

本文研究了一致可微的单圈T函数的性质,首先通过讨论参数概念在非阿基米德理论中的含义,给出了两种理论中单圈T函数判定条件的联系,说明了非阿基米德理论中的判定条件适用于部分由偶参数构造的T函数.另一方面,考察了单圈T函数最高分位输出序列的保熵性,说明了一般T函数不具有保熵性,而对于模4一致可微且具有相似结构的单圈T函数,其最高分位序列保熵性等价于当输入规模较小时最高分位序列的保熵性,为研究具有相似结构T函数的多样性提供了理论基础.

[1]A Klimov,A Shamir.A new class of invertible mappings[A].CHES 2002[C].Berlin:Springer-Verlag,LNCS 2523,2003.470-483.

[2]A Klimov,A Shamir.Cryptographic applications of T-functions[A].SAC 2003[C].Berlin:Springer-Verlag,LNCS 3006,2003.248-261.

[3]A Klimov,A Shamir.New cryptographic primitives based on multiword T-functions[A].FSE 2004[C].Berlin:Springer-Verlag,LNCS 3017,2004.1-15.

[4]J Hong,D Lee,Y Yeom,D Han.A new class of single cycle t-functions[A].FSE 2005[C].Berlin:Springer,LNCS 3557,2005.68-82.

[5]V Anashin,A Bogdanov,I Kizhvtov,S Kumar.ABC:A new fast flexible stream cipher [EB/OL].http://www.ecrypt.eu.org/ stream,2005.

[6]A Maximov.A new stream cipher “Mir-1” [EB/OL].http://www.ecrypt.eu.org/stream,2005.

[7]N Kolokotronis.Cryptographic properties of nonlinear pseudorandom number generators[J].Designs Codes & Cryptography,2008,46:353-363.

[8]N Kolokotronis.Cryptographic properties of stream ciphers based on t-functions[A].ISIT 2006[C].USA:IEEE,2006.1604-1608.

[9]W Y Zhang,C K Wu.The Algebraic normal form,linear complexity and k-error linear complexity of single-cycle t-fFunction[A].SETA 2006[C].Berlin:Springer,LNCS 4086,2006.391-401.

[10]游伟,戚文峰.单圈T函数的2-adic复杂度及1-错2-adic复杂度[J].通信学报,2014,35(3):135-139.

You Wei,Qi Wen-feng.The 2-adic complexity and the 1-error 2-adic complexity of single cycle T-functions[J].Journal on Communications,2014,35(3):135-139.(in Chinese)

[11]V Anashin.Non-Archimedean analysis,T-functions,and cryptography[EB/OL].http://arxiv.org/abs/cs/0612038,2006.

[12]V Anashin.Uniformly distributed sequences of p-adic integers[J].Mathematical Notes,1994,55(2):109-133.

[13]V Anashin.Uniformly distributed sequences of p-adic integers,II[J].Discrete Math Appl,2002,12(6):527-590.

[14]V Anashin.Pseudorandom number generation by p-adic ergodic transformations[EB/OL].http://arxiv.org/abs/cs.CR/0401030,January 2004.

[15]V Anashin,A Khrennikov,E Yurova.T-functions revisited:New criteria for bijectivity/transitivity[J].Designs Codes & Cryptography,2014,71(3):383-407.

[16]T Shi,V Anashin,D D Lin.Linear Weaknesses in T-functions[A].SETA 2012[C].Berlin:Springer-Verlag,LNCS 7280,2012.279-290.

[17]T Shi,V Anashin,D D Lin.Fast Evaluation of T-functions via Time-Memory Trade-Offs[A].Informations Security and Cryptology 2012[C].Berlin:Springer,LNCS 7763,2013.263-275.

[18]Huang M Q.Analysis and cryptological evaluation of primitive sequences over an integer residue ring[D].Beijing:Graduate School of USTC,1988.

[19]Dai Z D.Binary sequences derived from ML-sequences over rings I:periods and minimal polynomials[J].Journal of Cryptology,1992,5(3):193-207.

[20]Huang M Q,Dai Z D.Projective maps of linear recurring sequences with maximal p-adic periods[J].Fibonacci Quart,1992,30(2):139-143.

[21]A S Kuzmin,A A Nechaev.Linear recurring sequences over Galois rings[J].Algebra & Logic,1995,34(2):87-100.

王森鹏 男,1990年出生,河南商丘人.解放军信息工程大学硕士生,主要研究方向:密码学与信息安全.

E-mail:wsp2110@126.com

刘 燕(通信作者) 女,1990年出生,江苏无锡人,解放军信息工程大学硕士生,主要研究方向:密码学与信息安全.

E-mail:awhxxsbb@126.com

On the Properties of T-functions with Uniform Differentiability

WANG Sen-peng,LIU Yan,HU Bin

(ThePLAInformationEngineeringUniversity,Zhengzhou,Henan450001,China)

Combining conventional theory with non-Archimedean theory,we study the properties of T-functions.We focus on the criteria of single cycle T-functions and entropy preservability of the most significant bit output sequence generated by T-functions.Utilizing the parameters,the connection between criteria of single cycle T-functions in two different theories is established.The situation each criterion is suited for is cleared.On the other hand,we define the notion of entropy preservability of T-functions.We talk about the entropy preservability of most significant bit output sequences generated by T-functions with uniform differentiability.We present the condition for entropy preservability of most significant bit output sequences and show the transitivity.

T-functions;uniform differentiability;parameter;entropy preservability

2015-03-12;

2016-02-01；责任编辑：马兰英

国家自然科学基金(No.61272041，No.61502532)

TN918.1

A

0372-2112 (2016)11-2676-06

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.11.016