采用混合特征相似性的极化SAR图像降噪算法

杨学志，叶 铭，周 芳，郎文辉，郑 鑫，李国强

(1.合肥工业大学计算机与信息学院，安徽合肥 230009； 2.光电技术控制重点实验室,河南洛阳 471009)



采用混合特征相似性的极化SAR图像降噪算法

杨学志1，2，叶 铭1，周 芳1，郎文辉1，郑 鑫2，李国强2

(1.合肥工业大学计算机与信息学院，安徽合肥 230009； 2.光电技术控制重点实验室,河南洛阳 471009)

针对极化合成孔径雷达(Polarimetric Synthetic Aperture Radar,PolSAR)图像在相干斑抑制过程中面临的结构信息和极化散射信息保持的问题，通过分析PolSAR图像的结构特性和极化特性，建立一种结构特征提取方法，并提出一种采用混合特征相似性的极化SAR图像降噪算法.该算法将图像的结构信息和极化散射信息与降噪过程相融合，能够在抑制相干斑噪声的同时，实现降噪后图像的结构信息和极化信息的有效保持.实测机载极化SAR数据的实验结果验证了算法的有效性.

极化SAR；相干斑抑制；结构相似性；极化散射信息

1 引言

相干斑是极化合成孔径雷达(PolSAR)的多维相干成像系统固有缺陷导致的类噪声现象，它的存在不仅影响了图像的质量，还妨碍了地形分类[1]和目标检测[2]等的解译工作.因此对PolSAR图像进行有效的相干斑抑制就成为图像解译预处理的关键环节，具有重要的理论意义和研究价值[3].

具有结构信息和极化散射信息保持良好的PolSAR图像滤波算法，能够降低图像分割和分类等问题的难度，为实现地物场景的准确解译提供一个良好的基础.按照滤波时是否融入PolSAR图像的某些特征，一般将滤波算法大致分为以下三类：

(1)未融入PolSAR图像的特征：比如成像后的多视处理方法，极化白化滤波器[4](Polarimetric Whitening Filtering,PWF)，基于乘性噪声模型实现的极化Lee滤波算法[5]等等.这类算法简单有效，但是降噪后图像会损失一些信息，比如多视处理方法会模糊图像的结构.

(2)融入PolSAR图像的特征：例如融入了边缘结构特征的精致Lee(Refined Lee)算法[6]，以及加入像素的散射机制的Scattering-Model-Based滤波算法[7]，基于最小均方误差(Minimum Mean Square Error,MMSE)估计的联合结构判断和极化分解的混合滤波器[8]以及结构保持的双边滤波算法[9]等.该类算法对滤波后图像的结构信息或者极化散射信息保持较好，但相干斑的抑制能力会受到限制.

(3)隐式融入PolSAR图像的特征：这类算法主要是将目前处理自然图像和SAR图像的优秀滤波算法推广应用到PolSAR图像，它们不仅延续了原始算法对结构信息的有效保持性能，还充分利用PolSAR数据的极化特性.例如迭代双边滤波算法[10,11]，Pretest算法[12]，DSM算法[13]、NL-Lee算法[14]等一些基于非局部均值滤波的其他算法[15～17]，以及改进的极化Sigma滤波[18]等，这些算法都较好地保持了图像的结构特征和极化散射特性.

虽然上文第三类滤波算法也能获得不错的滤波性能，但为了更充分的利用PolSAR图像的结构信息和极化散射信息，进一步提高它们在降噪后图像中的保持性能，本文提出一种采用混合特征相似性的双边滤波算法(Hybrid Feature Similarity Bilateral Filtering,HFSBF).该算法不仅继承了双边滤波算法处理PolSAR图像的优势，还将结构信息和极化散射特性融入降噪过程，主要优势表现在以下两个方面：

(1)在极化总功率图(又称Span图)上提取PolSAR图像的结构信息，构建结构相似性度量函数，并取代原始双边滤波的空间域权重函数，提高结构保持能力.

(2)为增加提取极化散射信息的准确性，极化分解前对PolSAR数据进行去取向处理，再进行无监督分类，从而降低分类错误率.

2 PolSAR数据和双边滤波算法

对于PolSAR数据，一般采用后向散射矩阵精确描述地物目标.为了更好的从散射矩阵中提取目标的物理信息，通常将散射矩阵进行矢量化，对于单基站的PolSAR系统，散射矩阵在Pauli基和Lexicographer基下矢量化为：

(1a)

(1b)

其中Smn为散射矩阵中的元素，m,n∈{h,v}，表示发射入射波n，接收散射波m.上标T表示转置.通过向量kL和kp可以分别计算得到协方差矩阵C和相干矩阵T：

(2a)

(2b)

这里的<·>表示统计平均，上标H表示对复向量的共轭转置.由于kp能更好地表示目标的物理散射信息，所以T矩阵应用比C矩阵广泛，本文均采用T矩阵作为滤波输入.

(3)

(4)

(5)

σs表示空间域中控制平滑程度的参数，表示极化域中控制平滑程度的参数.d(i,j)为2范数，表示欧氏距离，d(Ti,Tj)描述的是两个相干矩阵间的相似性，文献[10,11]中使用了不同的度量措施，并取得不错的滤波效果.

3 采用混合特征相似性的PolSAR图像双边滤波算法

双边滤波算法在空间域上采用像素的空间位置来度量像素间的相似性，在滤波窗口内可能存在位置较远而结构相似的像素，使得滤波时赋予较小的权值而导致相干斑抑制效果不明显.此外，PolSAR图像的像素还包含物理散射信息，滤波时不加区分的对像素进行平均处理会损失极化散射信息.为解决这两个问题，本文提出HFSBF算法，该算法通过提取Span图的结构相似性指数构建空间域上的结构相似性度量函数；同时对Freeman-Durden分解前的PolSAR数据进行去取向处理，提高无监督分类的准确率，并以分类后的地物散射标记图为掩膜，按照像素的极化散射信息实现同质像素的选择和像素的相似性度量；最终提高滤波后图像的结构信息和极化散射信息的保持能力.

通过以上分析，HFSBF算法可以概括为两个方面：图像的结构相似性描述和极化散射信息提取.本节余下部分将以这两个方面为主，详细介绍HFSBF算法.

3.1 PolSAR图像的结构相似性权重函数的构建

结构相似性指数(Structure Similarity Index Measure,SSIM)是图像客观质量评价的一种常用方法[20]，它将图像的亮度、对比度和结构信息结合起来，能够度量滤波前后图像结构信息的相似性，很好的评价滤波图像结构信息的损失程度，并且能够与人眼对结构信息的视觉感知相一致.因此，引入SSIM来衡量图像块间的相似性.

(6)

其中μi和σi分别表示以像素i为中心的矩形窗Ni像素灰度的均值和标准差，σij是矩形窗Ni和Nj灰度值的协方差.ε1和ε2分别为防止零除特殊情况下的极小常数.

用高斯欧氏距离权重函数ws来衡量相似性时，d(i,j)的值越小，表示二者越相似.而SSIM的取值范围是[-1,1]，当SSIM的值越大时，表明块间的相似性越好.为了与高斯欧氏距离权重函数一致，我们定义如下的结构相似性权重函数：

(7)

从式(7)可以得到，其与ws单调性一致，当两相似块相同时，权值最大.

在对PolSAR图像进行相干斑抑制时，在Span图上计算SSIM的值.SSIM(i,j)是以像素i和j为中心的两个图像块通过式(6)计算得到的.PolSAR图像不仅含有丰富的结构信息，还含有很多的极化散射信息，为了更好的保持图像的结构信息和极化信息，需要将图像的极化散射信息融入滤波过程中.

3.2 极化散射信息的提取

为保持滤波后PolSAR图像的极化特性，每个像素在相干斑抑制过程中最好能够按照所属散射类分别进行滤波.这时就需要对PolSAR数据进行极化分解，但传统的做法是对原始的PolSAR数据进行分解，然而相同的散射目标可能会具有不同的取向，这样会导致两个取向不同而其它特征相同的散射目标会出现误分类情况.为减少误分类概率，提高滤波后图像的极化散射信息的保持能力，本文在进行极化分解之前，对PolSAR数据进行去取向处理[21]，

(8)

其中，

(9)

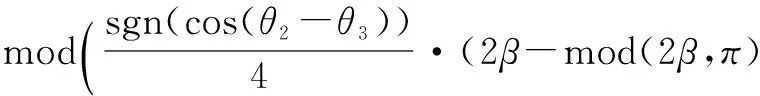
+mod(tan-1(tan2β·|cos(θ2-θ3)|),π)),π/2)

(10)

为获取PolSAR数据的极化散射特性，首先利用Freeman-Durden分解算法[22]将Td的每个像素分解成三个基本散射类：面散射、偶次散射和体散射.然后采用复Wishart分类器对三个基本散射类进行无监督分类[23]，并得到最终的分类标记图.为减少滤波后极化信息的损失，滤波时以分类标记图为掩膜，在滤波窗口中，只有与当前滤波像素具有相同分类标记号的像素贡献权值，即按照像素的散射相似性进行滤波，因此极化域内的权重函数wp可以修正为：

(11)

δ(·)是deta函数，当像素i，j的分类标记号相同时，δ(·)=1，否则为0.这样在相干斑抑制过程中，能够选择具有相同散射特性的像素参与滤波，能更好的保持极化信息.在本文中，矩阵间的相似性采用一种基于假设检验的Wishart分布矩阵的对数似然比来度量[12]，

d(Ti,Tj)

(12)

其中n表示视数，q表示通道数.

3.3 混合特征相似性的双边滤波算法

相比传统的双边滤波算法，本文将PolSAR图像的结构相似性和极化散射信息相结合，在相干斑抑制时，更好的保持了图像的结构信息和极化信息.为提高滤波性能，所提方法采用迭代的双边滤波策略，

(13)

通过以上分析，所提算法的详细步骤表示为：

步骤1 设定滤波窗大小Ni，在Span图上对邻域内的每个像素j利用式(6)和式(7)计算结构相似性权重值wSSIM(i,j)；利用式(8)对原始PolSAR数据进行去取向，再进行Freeman-Durden分解并分类，最后以分类标记图为掩膜，在邻域内利用式(11)计算修正后的极化域权重值wp,ref(i,j).

步骤2 将步骤1中所得到的权重值代入式(13)，得到单次迭代的滤波结果.

步骤3 在上一次迭代滤波结果的基础上，计算新的span图，并在新的span图上计算新的结构相似性权重值wSSIM，new(i,j)，将wp,ref(i,j)和wSSIM，new(i,j)代入式(13)进行下一次滤波.

在步骤3中，仍然使用原始数据中获得的极化域权重值wp,ref(i,j)，主要是因为：像素的散射机制是PolSAR数据重要的特性，迭代滤波必然会破坏像素的散射机制，从而会影响后续PolSAR图像分割与分类的准确性.为更好的保持像素的散射机制，并不从每次迭代后的极化数据中提取极化散射特性，而是仍使用原始数据中提取的极化散射特性.

4 实验结果与分析

4.1 实验数据及参数设置

为验证算法的有效性，对滤波结果进行定性和定量分析，并与Refined Lee，迭代双边滤波算法(KLBF[10],CBLF[11])和Pretest滤波器进行比较.使用两组机载SAR数据，第一组是AIRSAR获取的San Franscio Bay的极化数据，该测试数据是4视的，空间分辨率为10m×10m，图像尺寸为300×300.第二组是Convair获取的Ottawa地区的极化数据，测试数据是10视的，空间分辨率为64cm×10m，图像尺寸为340×220.

在实验测试中，Refined Lee，KLBF和CBLF的滤波窗大小设定为7×7，Pretest滤波器参数设置与文献[12]中相同.HFSBF滤波窗口设置大小为9×9，最终分类数为15类.算法的迭代次数将影响图像结构特征的保持能力以及相干斑噪声的抑制能力.迭代次数过少，将导致噪声抑制不足，而迭代次数过多，将增加对结构特征的破坏.根据对多幅测试图像的滤波性能分析，KLBF、CBLF和HFSBF算法中迭代次数t均设定为3次.

4.2 实验结果与讨论

图1显示了两组测试数据滤波前后的pauli RGB分解后的伪彩色图，通过比较发现这几种算法对相干斑具有一定的抑制能力.Refined Lee和CBLF算法的边缘较模糊，同时在一些区域出现了块效应.KLBF算法在细节丰富区域会出现过平滑现象.Pretest算法和HFSBF在边缘，线目标的保持上相对于其他算法都是较好的，但相比某些强点目标，比如图1(f1)中箭头所指，Pretest算法的强点保持没有HFSBF算法好.

为了定量分析滤波结果，分别计算出了滤波前后图像的等效视数(Equivalent Number of Looks,ENL)[10]，基于比值的边缘保持指数(Edge Preservation Degree based on the Ratio of Average,EPD-ROA)[24]以及无参考空域图像质量评价指数(Blind/Referenceless Image Spatial Quality Evaluator,BRISQUE)[25]，他们分别描述了滤波后图像的相干斑抑制能力(其值越大越好)、边缘保持性能(其值越大越好)和图像的失真度(其值越小越好).

表1和表2计算出了两组测试数据在三种不同评价指标下的值，其中EPD-ROA-H和EPD-ROA-V分别表示在水平方向和垂直方向上的值.对于第一组测试数据，通过比较可以发现三个指标的值都是最好的，第二组数据在边缘保持方面是最好的，滤波后图像的质量仅次于Refined Lee滤波算法，相干斑抑制能力跟Pretest算法相当.

为了能够从视觉上更好的显示出本文算法的结构保持能力，图2示出了两组测试数据滤波前后Span图的比值图像.通过两组测试数据的比值图，可以得到，Pretest和本文所提方法的比值图像是最模糊的，说明滤波过程中损失的图像结构信息少，这也与表1和表2中的EPD-ROA值相符合.

表1 SanFranscio测试数据EPD-ROA、BRISQUE和ENL值

EPD-ROA-HEPD-ROA-VBRISQUEENLRefinedLee0.93730.957114.136454CBLF0.92880.950430.6329132KLBF0.94570.965113.0171167Pretest0.93870.953622.9666157HFSBF0.95760.973312.5028191

表2 Ottawa测试数据EPD-ROA、BRIQUSE和ENL值

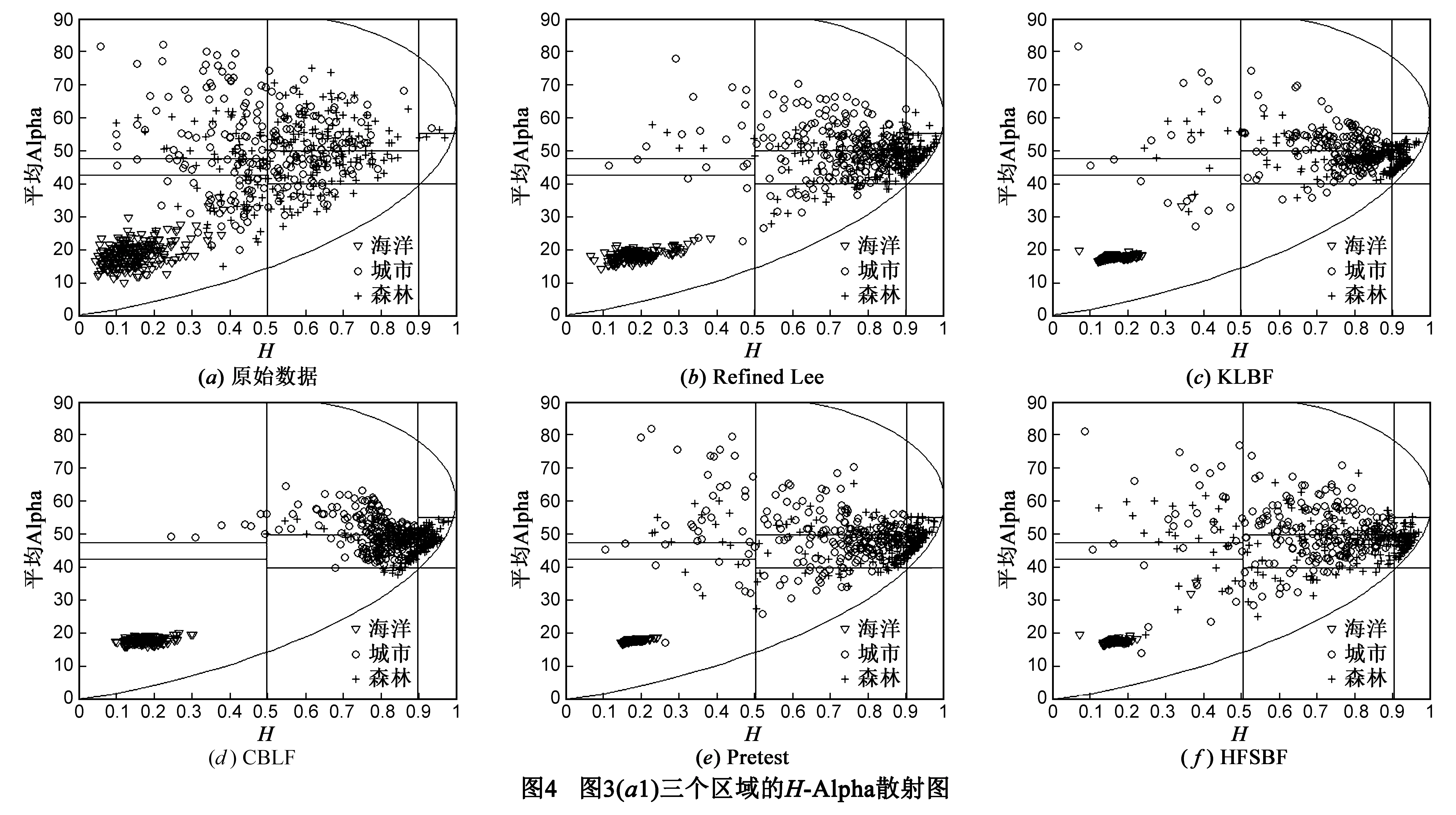
极化散射特性是PolSAR数据的重要特性，相干斑抑制过程中极化散射特性的保持能够直接影响PolSAR图像分割、分类的准确性.极化熵H和平均Alpha角是表征PolSAR数据极化散射特性的两个重要参数[12].图3是两组测试数据滤波前后的熵值图，图3(a1)和图3(a2)是原始数据的熵值图，由于没有进行滤波处理，他们的熵值都很低，地物结构不易区分.滤波处理后，两组测试数据的熵值增加，不同散射类型的地类结构能够很好地被区分开来.当熵值图的某些区域很亮(熵值增加)时，表明该区域空间分辨率损失很大，从另一个方面也验证了图像边缘损失严重.从熵值图，我们还可以发现本文所提方法在结构丰富区域的熵值相比其他方法都较低，说明了这些区域结构信息保持很好.

通过以上对滤波后PolSAR图像的相干斑抑制能力，结构保持能力和极化散射特性的保持能力分析，可以得到：相比实验对比的PolSAR图像的相干斑滤波器，本文所提算法不但具有较好的相干斑抑制能力，而且在结构信息的保持和极化信息的保持能力上也具有一定的优势.

4.3 算法运算时间

对HFSBF、Refined Lee、KLBF、CBLF和Pretest五种算法的实际运算时间进行实验比较与分析.各算法的参数采用其缺省设置，其中HFSBF、KLBF、CBLF经过了3次迭代滤波，而Refined Lee和Pretest只有1次滤波.各算法对San Francisco Bay(尺寸为300×300)和Ottawa(尺寸为340×220)两幅SAR图像的运算时间如表3.从表3的结果看出，HFSBF算法运行时间最长，其中极化分类在San Francisco Bay和Ottawa上分别耗时12s和11s.五种算法均在C++软件上运行，进行实验的计算机配置是3.06GHz Pentium(R)Dual-Core CPU，1.96GB内存.

表3 各算法运行时间

本文工作着重研究通过极化分类来提高滤波算法对极化信息与结构信息的保持能力.然而，极化分类过程的引入也导致了运算量的增加.未来的工作将进一步研究通过简化极化分类过程来减少算法运算量.

5 总结

针对PolSAR图像的结构信息和极化散射信息保持的难点问题，本文提出一种采用混合特征相似性的双边滤波算法.该算法结合图像的结构相似性和极化散射特性，将构建的结构相似性权重函数和去取向后的地物散射标记图引入迭代双边滤波算法过程中.通过提高地物散射标记图的分类精度和图像的结构相似性描述，使得该算法能够在相干斑抑制同时，更好的保持了图像的结构信息和极化散射信息.

[1]Kersten P R,Lee J S,Ainsworth T L.Unsupervised classification of polarimetric synthetic aperture radar images using fuzzy clustering and EM clustering[J].IEEE Transactions on Geoscience and Remote Sensing,2005,43(3):519-527.

[2]Shirvany R,Chabert M,Tourneret T Y.Ship and oil-spill detection using the degree of polarization in linear and Hybrid/Compact Dual-PolSAR[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012,5(3):885-892.

[3]Lee J S,Ainsworth T L,Wang Y T.On polarimetric SAR speckle filtering[A].IEEE International Geoscience and Remote Sensing Symposium[C].Munich,German,2012.111-114.

[4]Liu G Q,Huang S J,Torre A,et al.The multilook polarimetric whitening filter(MPWF)for intensity speckle reduction in polarimetric SAR images[J].IEEE Transactions on Geoscience and Remote Sensing,1998,36(3):1016-1020.

[5]Lee J S,Pottier E.Polarimetric Radar Imaging:From Basics to Applications[M].Boca Raton:CRC Press,2009:157-160.

[6]Lee J S,Grunes M R,Grandi G D.Polarimetric SAR speckle filtering and its implication for classification[J].IEEE Transactions on Geoscience and Remote Sensing,1999,37(5):2363-2373.

[7]Lee J S,Grunes M R,Schuler D L,et al.Scattering-model-based speckle filtering of polarimetric SAR data[J].IEEE Transactions on Geoscience and Remote Sensing,2006,44(1):176-187.

[8]Ding Z G,Zeng T,Dong F,et al.An improved PolSAR imgae speckle reduction algorithm based on structural judgment and hybrid four-component polarimetric decomposition[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(8):4438-4449.

[9]杨学志，叶铭，吴克伟，郎文辉，郑鑫，李国强.结构保持的双边滤波极化SAR图像降噪[J].电子与信息学报，2015,37(2):268-275.

Yang Xue-Zhi,Ye Ming,Wu Ke-Wei,Lang Wen-Hui,Zheng Xin,Li Guo-Qiang.Speckle Reduction for PolSAR Image Based on Structure Preserving Bilateral Filtering[J].Journal of Electronics & Information Technology,2015,37(2):268-275.(in Chinese)

[10]D’Hondt O,Guillaso S,Hellwich O.Iterative bilateral filtering of polarimetric SAR data[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2013,6(3):1628-1639.

[11]Alonso-González A,López-Martínez C,Salembier P,et al.Bilateral Distance based filtering for Polarimetric SAR data[J].IEEE Transactions on Geoscience and Remote Sensing,2013,5(11):5620-5641.

[12]Chen J,Chen Y L,An W T,et al.Nonlocal filtering for polarimetric SAR data:a Pretest approach[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(5):1744-1754.

[13]Liu G C,Zhong H.Nonlocal means filter for polarimetric SAR data despeckling based on discriminative similarity measure[J].IEEE Geoscience and Remote Sensing Letters,2014,11(2):514-518.

[14]Zhong H,Zhang J J,Liu G C.Robust Polarimetric SAR despeckling based on nonlocal means and distributed Lee filter[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(7):4198-4210.

[15]杨学志，左美霞，郎文辉，张晰，孟俊敏.采用散射特征相似性的极化SAR图像相干斑抑制[J].遥感学报，2012,16(1):110-114.

Yang X,Zuo M,Lang W,et al.Speckle reduction for multi-polarimetric SAR image with the similarity of the scattering[J].Journal of Remote Sensing,2012,16(1):110-114.(in Chinese)

[16]赵忠民，赵拥军，牛朝阳.改进的基于非局部均值的极化SAR相干斑抑制[J].中国图象图形学报，2013,18(8):1038-1044.

Zhao Z,Zhao Y.Improved polarimetric SAR speckle filter based on non-local means[J].Journal of Image & Graphics,2013,18(8):1038-1044.(in Chinese)

[17]Torres L,Sant’Anna S J,Freitas C,Frery A C.Speckle reduction in polarimetric SAR imagery with stochastic distances and nonlocal means[J].Pattern Recognition,2013,47(1):141-157.

[18]Lee J S,Ainsworth T L,Wang Y T,Chen K S.Polarimetric SAR speckle filtering and the extended sigma filter[J].IEEE Transactions on Geoscience and Remote Sensing,2015,53(3):1150-1160.

[19]Li T G,Wang C L,Huang P P,et al.SAR image despeckling using a space-domain filter with alterable window[J].IEEE Geoscience and Remote Sensing Letters,2013,10(2):263-267.

[20]Wang Z,Bovik A C,Sheikh H R,et al.Image quality assessment:from error visibility to structural similarity[J].IEEE Transactions on Image Processing,2004,13(4):600-612.

[21]Xu F,Jin Y Q.Deorientation theory of polarmetric scattering targets and application to terrain surface classification[J].IEEE Transactions on Geoscience and Remote Sensing,2005,43(10):2351-2364.

[22]Freeman A,Durden S L.A three-component scattering model for polarimetric SAR data[J].IEEE Transactions on Geoscience and Remote Sensing,1998,36(3):963-973.

[23]Lee J S,Pottier E,Ferro-Famil L.Unsupervised terrain classification preserving polarmetric scattering characteristics[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(4):722-731.

[24]Feng H X,Hou B,Gong M G.SAR image despeckling based on local homogenous-region segmentation by using pixel-relativity measurement[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(7):2724-2737.

[25]Mittal A,Moorthy A,Bovik A.No-reference image quality assessment in the spatial domain[J].IEEE Transactions on Image Processing,2012,21(12):4695-4708.

杨学志(通信作者) 男，1970年9月出生，安徽合肥人.教授、博士生导师、国际模式识别协会遥感技术分会会员.2003年毕业于香港大学电机与电子工程系，获博士学位，2006年至2007年于加拿大滑铁卢大学系统设计工程系从事SAR海冰图像解译的博士后研究.现为合肥工业大学计算机与信息学院副院长，主要从事数字图像处理、模式识别、计算机视觉、合成孔径雷达遥感图像处理等方面的研究工作.

E-mail:xzyang@hfut.edu.cn

叶 铭 男，1989年10月出生，安徽安庆人.2015年毕业于合肥工业大学计算机与信息学院，获硕士学位.研究方向为图像处理、合成孔径雷达图像解译.

E-mail:yemhfut@163.com

Speckle Reduction for PolSAR Images Using Hybrid Features Similarity

YANG Xue-zhi1,2,YE ming1,ZHOU Fang1,LANG Wen-hui1,ZHENG Xin2,LI Guo-qiang2

(1.SchoolofComputerandInformation,HefeiUniversityofTechnology,Hefei,Anhui230009,China; 2.ScienceandTechnologyonElectro-OpticControlLaboratory,Luoyang,Henan471009,China)

The preservation of structural information and polarimetric scattering properties is the major obstacle in despeckling for Polarimetric Synthetic Aperture Radar(PolSAR)images.Speckle reduction for PolSAR images using hybrid features similarity,to establish a method for extracting structural features by analyzing the structural feature and polarimetric information of PolSAR data,is proposed.The proposed method introduces structural characteristics as well as polarimetric scattering characteristics into the speckle reduction and in order to preserve them efficiently after filtering.The test results of real airborne SAR data show the effectiveness of the algorithm.

polarimetric SAR;speckle reduction;structure similarity;polarimetric scattering characteristics

2015-03-31;

2015-10-11;责任编辑：马兰英

国家自然科学基金(No.61371154，No.41076120，No.61271381，No.61102154);光电控制技术重点实验室和航空科学基金联合资助项目(No.201301P4007);中央高校基本科研业务费专项资金(No.2012HGCX0001)

TN911.23

A

0372-2112 (2016)11-2583-09

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.11.004