黄泛平原结构性低液限土的先期固结压力确定

史翠英，寇　婷，沙　俊

（江苏省地矿局第五地质大队，江苏徐州221004）

黄泛平原结构性低液限土的先期固结压力确定

史翠英*，寇婷，沙俊

（江苏省地矿局第五地质大队，江苏徐州221004）

以黄泛区平原低液限土为研究对象，在对比、分析了原状土与重塑土的一维单向固结压缩曲线形态后认为：黄泛平原低液限土是一种具有结构性的土，且经试验结果证实土的结构强度较弱。经采用双对数坐标法和还原曲线法来确定土的结构屈服应力及先期固结压力，结果证实：①双对数坐标法同样适用于低液限土的结构屈服应力求解；②传统试验方法及Casagrande法确定结构性低液限土的先期固结压力是不合适的；同时初步探讨了黄泛平原土的结构性特征。

黄泛平原；土的结构性；低液限土；先期固结压力

土的结构性，是指土体颗粒和孔隙的性状和排列形式（又称组构）及颗粒之间的相互作用。土结构性对土体的应力—应变、强度、渗透等工程性质有着强烈的影响，从而引发人们的广泛关注，并成为“21世纪土力学的核心”研究课题[1]。近年来的研究表明：各地区、各种类型的土都存在着结构性，而且不同成因，不同类型，不同内部结构的土，其结构性有着极大的差异。然而，对于成因特殊，分布区域广泛的黄泛区平原土的结构性研究却鲜见文献。

研究表明，黄泛平原区因黄河的冲淤积作用，区内土质呈层状分布，土质以低液限粉土、粉质粘土为主（局部夹有高液限粘土层）；土中矿物成分中非粘土矿物（石英、长石等）含量高（最高达89%）；粘土矿物含量低（平均26%，最低11%）[2]，土的工程特性表现为低塑性、高密度、低强度、中压缩性等[3]。对取自济南北某施工现场土样，进行室内试验，对区内土的结构性及其对土的先期固结压力这一土性指标的影响予以探究，期望据此引发同行关注。

1　土的性质与试验

1.1土的性质

在钻探现场，沿钻孔不同深度取原状样三件，并依照《公路土工试验规程》（JTG40-2007）测试土的各项土工参数，同时制作对应的重塑样，控制重塑样的含水率、孔隙比与原状土相近。土的主要物性指标见表1。由表1可见试样具有黄泛区平原土质特征：表现为土的天然密度较大，孔隙比较小，土在天然状态下密实；依土的液限和塑性指数，按规程（JTG40-2007）塑性图分类，应属低液限土；土的颗粒组分显示，土中粒组分散度不高，主要以粉粒组为主，粘粒含量较低。

表1　土的主要物性指标

1.2试验

试验采用KTG-98全自动高压固结试验系统，可实现加荷、判稳及数据采集的全自动控制，加荷速率取1，即试验压力设置为：12.5、25、50、100、200、400、800、1600、3200（kPa）共9级。考虑到该类土在有侧限单向固结条件下，沉降稳定较缓慢（张朋等）的特点，每级荷载历时4d再施加下一级荷载，以获取完整的试验成果。

2　试验成果与讨论

2.1土的结构性

如图1所示，为原状土与重塑土的压缩曲线。由图1可见：

（1）原状土的压缩曲线在初始低压力段曲线变化平缓，随着试验压力的增大，曲线出现陡降；再增大试验压力，曲线变化又趋缓，即原状土的压缩曲线变化呈缓慢-陡降-趋缓的三段式。而对应重塑土的压缩曲线则是随着试验压力增大以近乎直线的形式变化，只是在试验压力大于1600kPa后才有所趋缓。对比原状土和对应重塑土的压缩曲线形态可以认为，试验所取土样是具有结构性的土。王立忠（2004）将原状土的压缩曲线形态分为2种：①三段式：平缓—陡降—再趋缓；②二段式：平缓—陡降，并认为具第①种曲线形态的土具有较强的结构性，而结构性的强弱与土的结构强度相关。试验表明，本文所取土为具有一定结构强度的结构性土。

（2）在相同的垂向压力下，原状土与对应重塑土之间存在一个孔隙比差Δe。这说明原状土在沉积过程中形成了某种形态的结构并且产生一定的结构强度，即土的结构屈服应力。当试验压力较小时，原状土的结构强度足以抵抗这种低应力作用而不致使土体产生较大变形，所以相对重塑土而言Δe较大；随着试验压力增大，原状土的结构性部分损伤，土的沉降开始加大；当试验压力达到或超过土的结构屈服应力σk后，原状土的结构崩溃，结构性丧失，处于结构屈服状态。原状土结构屈服后沉降量增大，压缩曲线变化陡降，Δe值快速减小，原状土压缩曲线向重塑土压缩曲线趋近。对于Δe值，Burland（1990）将其定义为附加孔隙比，用于定性表述土的结构性。

2.2土的结构强度

对于具有结构性的原状土而言，土的结构屈服应力σk值是描述土的结构强度的重要参数，而结构屈服应力σk的确定。目前通用的方法是依原状土在一维单向固结状态下的压缩曲线来确定。

2.2.1由Casagrande法确定σk值

传统的casagrande法（下文简称“C”法）所得出的是土的先期固结压力，但这只是针对非结构性土而言的。对于具有结构性的土，当压力超过土的结构屈服压力后，土的结构性丧失，沉降量增大，土处于结构屈服状态，表现在土的压缩曲线上就是曲线形态出现陡降（如图2所示）。因此，此时用“C”法所得应是原状结构性土的结构屈服应力σk，而不是通常意义上的先期固结压力[7]。

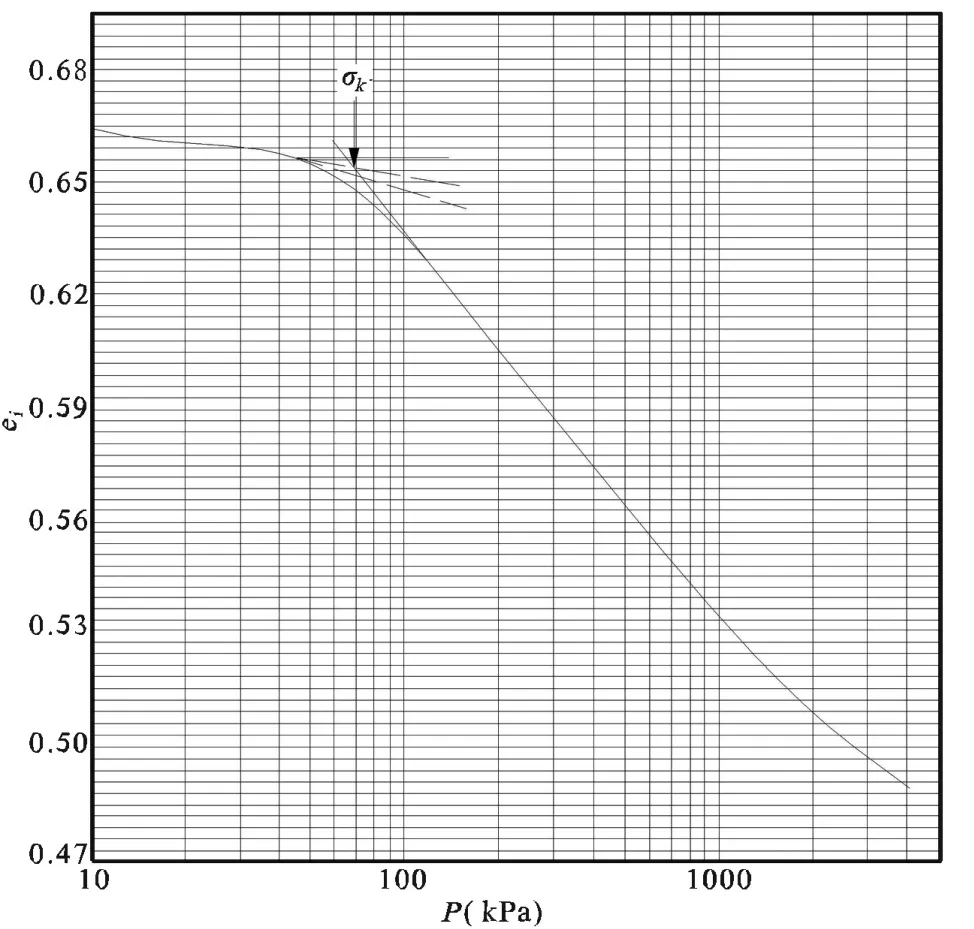
采用C法，本文所取原状土的结构屈服压力σk是：试样sy-1,

σk=70.3kPa；试样sy-2,σk=109.9kPa；试样sy-3, σk=138.6kPa；。

2.2.2双对数坐标法确定的σk值

由于采用C法确定结构性土的结构屈服压力时，存在着最大曲率点难以确定，而且结构性土在结构屈服后的压缩曲线形态并非完整的呈现直线形，从而使测试结果产生难以避免的偏差。对比，殷杰（2012）推荐使用Butterfield提出的双对数坐标法，并经他本人对中外39件原状样（软粘土）验证，有较好的适用性。

双对数坐标法就是用ln（1+e）-lgP双对数坐标来处理土的压缩试验成果。在该坐标系内，土的压缩曲线就形成2条相交的直线，其交叉点对应的试验压力即为土样的结构屈服应力σk，所对应的孔隙比即为土在结构屈服应力下的孔隙比。如图3所示。

由双对数坐标法得到的原状样的结构屈服应力是sy-1,σk=70kPa；试样sy-2,σk=110kPa；试样sy-3, σk=140kPa。与由“C”法所得值基本一致。这表明，双对数坐标法同样适用于黄泛平原结构性低液限土的结构屈服应力求解。

2.3土的先期固结压力确定

2.3.1改进后李涛模型

如上文所述对于具结构性的土而言，传统“C”法所确定的是该原状土的结构屈服应力σk。而由此得出的超固结比OCR值也只能称之为原状土的结构应力比。李涛（1987）等人的研究表明，依据土的压缩及回弹特性，可以从完全丧失结构强度的重塑土（称理想重塑土）来还原土的压缩性状并推求结构性土的先期固结压力，由此建立了还原土的压缩曲线的数学模型。

由于该模型只考虑了土是正常固结土或超固结土而没有考虑土结构性的影响。王国欣等（2003）经分析后认为用结构屈服压力σk代替原模型中的上覆压力P0，其他指标不变。改进后李涛数学模型为：

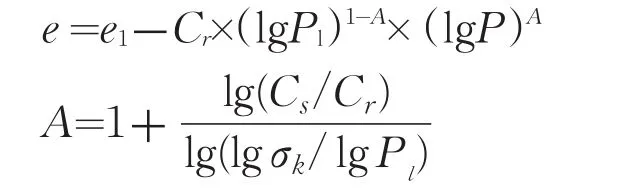
式中：e1——压力1kPa时对应的孔隙比，可用初始孔隙比e0代替；

Cr——理想重塑样的压缩指数，即理想重塑样压缩线斜率；

Cs——重塑样回弹指数；

σk——原状样结构屈服压力；

Pl——原状样与重塑样压缩曲线交点上对应压力值；

A——还原系数，它反映了还原后压缩曲线的特征。

改进后的李涛模型，经王国欣室内试验检验和鲍国胜（2012）实际工程应用，表明具有较好的实用性和较高的可靠性。

本文采用改进后的李涛模型来确定试样的先期固结压力。

2.3.2土样参数的确定

如图4所示为模型计算用土样参数的确定方法，这其中：

（1）理想压缩曲线是重塑土的初始孔隙比与原状土和重塑土交点的连线，该压缩曲线的斜率可用压力为100kPa和1000kPa及对应孔隙比代入计算。

（2）关于原状样与重塑样两压缩曲线的交点。本文所取试样的试验结果（图1）显示：原状样与对应重塑样的压缩曲线在试验压力范围内（≤3200kPa）没有交点。但可以采用依照压缩曲线趋势延长压缩曲线办法（王国欣，2003）获得两压缩曲线的交点。依此，本试验3件试样的压缩曲线交点位分别是：sy-1,0.739e0；试样sy-2,0.706e0；试样sy-3,0.684e0。

文献[9]介绍了薛迈特曼（Schmertmann）认为在土的密实程度接近和压力足够大时，原状土与扰动土的压缩曲线趋近并相交于孔隙比为0.42e0处。但经众多的试验成果考证，压缩曲线的交点并不都是042e0。例如：王立忠所做3件温州软土其交点位分别是0.622e0、0.574e0和0.647e0；而王国欣所做杭州海积软土的相交点位是0.59e0。本文所得实验结果其交点位也并不在0.42e0。可以认为，不同类型（成因）的原状土与重塑土其压缩曲线的相交点位是不尽相同的。

2.3.3还原压缩曲线

各参数确定后，应用改进后的李涛模型，计算出各压力级别下还原后压缩曲线孔隙比。如图5～图7即为本文所取试样还原后的压缩曲线，依此曲线再采用“C”法确定土的先期固结压力：sy-1，Pc=302kPa；sy-2，Pc=394kPa；sy-3，Pc=472kPa；

2.4土的结构性影响

2.4.1土的结构屈服应力与自重应力

将土的自重应力、结构屈服应力和还原前后土的先期固结压力等参数列于表2，可见各层位土的结构屈服应力均小于土的自重应力，这表明黄泛平原低液限土的结构强度较弱。

王国欣（2003）认为结构屈服应力是先期固结压力Pc与结构强度q之和；熊传祥（2002）对杭州软土的试验也证实土的结构屈服应力大于土的自重应力。这些结论对于粘土而言是正确的。而本文之所以得出截然相反的试验结果，笔者认为是土质差异所致。

由于黄泛平原的成土物源来自于黄土高原。土的物质组成中非粘土矿物含量占80%以上；颗粒组分中粉粒组大于80%（表1）；在黄河水流的长距离搬运作用下，土粒间相互碰撞、摩擦造成土粒表面磨圆度高，表面强度低[2]。土粒在沉积成土后，颗粒间直接接触，粒间缺少由粘土矿物所产生的絮胶状和无定型胶体物质，仅在上覆土层的自重应力作用下，土粒之间相互挤压、趋密，粒间相互咬合形成土的结构强度。

龚晓南（2000）在分析粘土结构性成因时认为：土的物质成分对结构性影响是第一位的。其中不同的粘土矿物，尤其是具膨胀性粘土矿物在土的沉积成土过程中节点变质、盐基交换、粒间胶结等系列作用，都能影响土的结构性。相比较，黄泛平原低液限土中粘土矿物含量极低，土粒间各种作用缺失；使得土体结构强度形成因素单一。所以，当土受到附加应力作用时土粒间的联结极易破损，土的结构性易丧失，就表现出表2中的结构屈服应力小于土的自重应力。

表2　土的部分力学特特性参数

对比不同深度下土的自重应力P0与结构屈服应力σk可见，随着土样埋深的增加，上覆土层的自重应力增大，土的结构屈服应力σk也随之增大，这种现象与软粘土的结构性表现一致（王立忠）。但结构屈服应力σk的增大幅度小于自重应力P0的变化。这表明土的结构性受成土环境影响同时这种影响对不同土质所产生的作用不同。

2.4.2土的结构性与压密状态

表2的试验结果还显示：采用传统的“C”法所确定的土的先期固结压力Pc值均小于土的自重应力，若依此判断各层土的压实状态均属“欠固结土”，显然这种判断是错误的。

事实上，早在数十万年前黄河就开始了塑造华北平原的历程，进入全新世，黄泛平原又经历了完整的海水进退旋回；自全新世到进入历史时期，黄河又发生了数十次泛滥、改道[14]。这些应力增减变化及漫长地质历史作用，使具一定埋深的土受到压密，达到在相应自重应力下的固结或超固结状态。但因试验过程中土结构性的影响，使传统的试验方法得出的土的压密状态判断与实际不符。但采用改进后的李涛模型还原后的Pc值，则能较准确反映土的压密状态。同时，比较表2中还原前后的先期固结压力Pc值与结构屈服应力σk值，实验结果证实传统试验方法所得出的是土的结构屈服应力而并非是土的先期固结压力。

3　结论

（1）黄泛平原低液限土是具有结构性的土；

（2）土的结构强度较弱，具体表现在土的结构屈服应力小于自重应力及还原后的先期固结压力；

（3）对具有结构性土的先期固结压力Pc值应采用还原压缩曲线的办法来确定，从而消除土结构性的影响。

[1] 沈珠江.土体结构性的数学模型——21世纪土力学的核心问题[J].岩土工程学报，1996，18（1）：1-6.

[2]姚占勇.黄河冲淤积平原土的工程特性研究[D].天津：天津大学，2006.

[3]张朋，刘桂才，李锋，等.黄河冲积平原低液限土的工程特性研究[J].地质学刊，2014，38（1）：154-158.

[4]JTG E40-2007公路土工试验规程[S].

[5]王立忠，丁利，陈云敏，等.结构性软土压缩性研究[J].土木工程学报，2014，37（4）：46-53.

[6]Burand,J,B.On the Compressibility and Shear Strength of Natu⁃ral Soils[J].Geotechnique，1990，40（3）:329-378.

[7] 王国欣，肖树芳，周旺高.原状结构性土先期固结压力及结构强度的确定[J].岩土工程学报，2003，25（3）：249-251.

[8]殷杰.土结构性对天然软粘土压缩性的影响[J].岩土力学，2012，33（1）：48-52.

[9]李涛，钱寿易.土样扰动影响的评价及其先期固结压力的确定[J].岩土工程学报，1987，9（5）：21-30.

[10] 鲍国胜，秦志光.原状结构性土先期固结压力的确定与分析[J].路基工程，2012（1）:85-88.

[11]王国欣.软土结构性及其扰动状态模型研究[D].吉林大学，2003.

[12]熊传祥，周建安，龚晓南，等.软土结构性试验研究[J].工业建筑，2002，32（3）35-37.

[13]龚晓南，熊传祥，项可祥，等.粘土结构性对其力学性质的影响及形成原因分析[J].水利学报，2000（10）：43-47.

[14]田广增，贺贵山..黄河对华北平原的“贡献”[J].殷都学刊：自然科学版，1997（4）：62-67.

P642

A

1004-5716（2016）11-0005-05

2016-01-13

2016-01-14

史翠英（1980-），女（汉族），江苏徐州人，工程师、注册岩土工程师，现从事岩土测试工作。