打车软件参与下出租车动态定价策略研究

张佳彤

(唐山学院 经济管理系，河北 唐山 063000)



打车软件参与下出租车动态定价策略研究

张佳彤

(唐山学院 经济管理系，河北 唐山 063000)

科技的发展以及智能手机的普及，有效地解决了信息传递问题，出租车司机可以通过打车软件平台实时传递出自己的服务水平、价格、地理位置等信息，乘客也可以通过打车软件平台表达其价格意愿、地理位置等信息。在此背景下，文章基于排队论设计了一种动态定价模型，对比传统的出租车定价模型，此模型可以提升公司收益，减少社会资源(消费者时间)的浪费；而在动态模型基础上设计的合乘模式的定价策略，也可以有效提高资源的利用率，缓解日趋紧张的交通压力。

出租车；动态定价模型；合乘动态定价策略；排队论

出租车行业是具有一定准公共物品性质的行业，政府对出租车市场进行着数量以及价格上的管制。关于管制的必要性，张相斌等人[1]在对巡游类出租车市场进行调查研究后认为，由于司机无法准确及时地传递出其车辆的服务水平从而表达提高或者降低价格的意愿，同时消费者也无法有效表达自己提高价格来换取高水平服务的意愿，因此在此状况下如果没有价格管制，整个市场会剥夺消费者剩余并趋向于无效率。随着科技的发展，智能手机的普及，Uber、滴滴出行等打车软件平台兴起，有效地改善了上述提到的信息传递问题，每一个司机都可以通过打车软件平台实时传递出自己的服务水平、价格、地理位置等信息，每一个乘客也都可以通过打车软件平台表达其价格意愿、地理位置等信息[2-3]。基于这种改变，滴滴和Uber都在其应用中推出了动态价格策略，但现在主要应用于专车、快车等业务，出租车价格依然在管制下使用传统的定价模式[4-5]。本文将在介绍传统的出租车定价模型基础上，基于排队论建立动态定价模型，通过讨论、对比得出最优的定价策略。

1 传统的出租车定价

传统的出租车定价主要基于供需关系、成本以及当地的居民收入水平来确定，主要包括的项目有起步价、每公里价格、燃油补贴以及等候费等。每项的具体价格会通过举行听证会的形式确定和调整。鉴于听证会举行的周期通常以年为单位，且基本价格构成没有较大的变化，因此，传统的出租车定价可以看作静态的价格策略[6-7]。

1.1 传统出租车价格的构成

(1)起步价：乘客乘坐时，未超过规定的起步公里数时的价格，是乘坐一次的最低价格。

(2)单位里程价：指出租车行驶里程大于起步价规定的起步里程后，每公里收费以单位里程价为准。常见的为超过1公里按2公里计算。

(3)燃油费：在油价上涨的大背景下，在相关部门要求下，建立了油价运价联动机制，目前以收取燃油费为主。

(4)夜间附加费：出租车在夜间工作时，收取高于白天的起步价或单位里程价。如上海、北京在夜间(23：00pm～5：00am)起步价和单位里程价上浮20%到30%。

(5)低速费：指通过计算出租车在低速(一般为10 km/h或者12 km/h)行驶的时间来计算的费用，用来补偿车辆低速行驶带来的油耗和时间消耗。

(6)长途空返费：远距离运输乘客，尤其以从市中心到郊区的路线，常常难以避免回程空驶而增加的成本。因此，部分城市的出租车收取长途空返费。一般以超过长途临界值(10～15 km)后，超出的部分以加收一定比例(30%～50%)费用的形式收取。

部分城市的出租车价格构成，如表1所示。

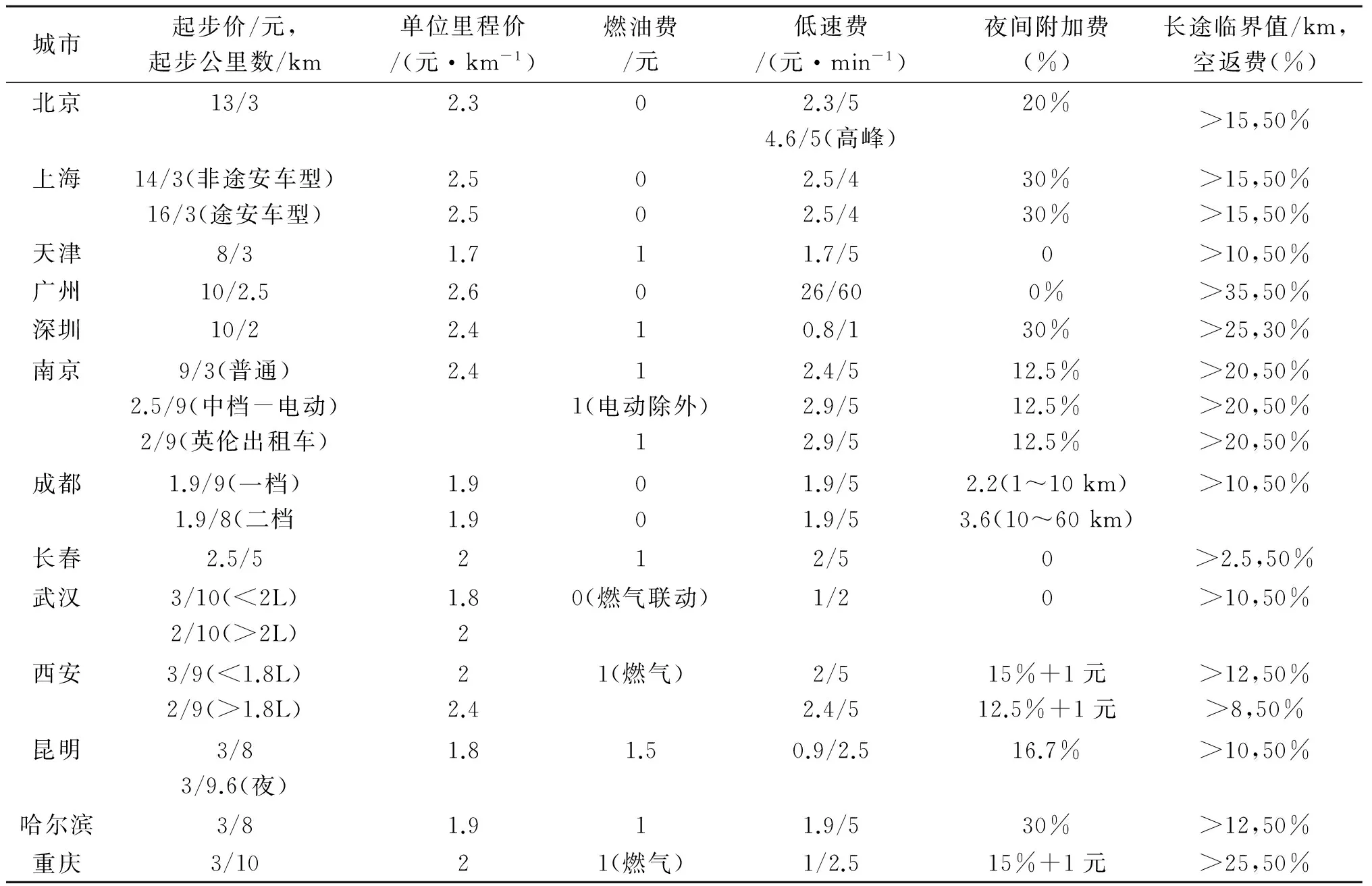
表1 部分城市出租车详细价格构成

1.2 传统出租车定价模型

由于起步价和单位里程价两个构成元素是上述几个因素中较为重要的，多数文献也是基于二者来建立传统出租车定价模型，因此，在下面的传统出租车定价模型中仅考虑了这两个元素：

式中：p——乘客出行费用(元)；C0——起步价格(元)；d——乘客的出行距离(km)；d0——起步里程(km)；C——单位里程价(元/km)。

2 出租车动态定价

对于乘客在获得出租车服务，特别是需要快速到达的情况，时间是一个重要的属性。当出租车提供快速服务的能力受到交通系统拥堵影响时，价格作为以拥堵情况而变化的函数对于解决拥堵、缓解交通压力来说是一个较好的策略，这就是所谓的出租车动态定价。动态价格作为收益管理中一种重要方法，已经应用在各个行业中来提高收益。比如，制造商根据提前期不同来设定不同的产品价格，提前期越短越精确的产品合同要价也相对越高；4S店里，现场买车的价格和等三个月后提车的价格肯定是不一样的；服务行业里，酒店住宿价格和航空机票价格的动态价格已经是收益管理里的经典案例。新兴的分享经济企业翘楚、Uber也推出了高峰价格(surgeprice)来协调乘客和可用车辆。对于同样需要提供快速到达服务的出租车，时间对于乘客感知的效用而言至关重要。

不同于其他行业，乘客的等待时间在出租车行业中可以较为直接地反映出市场的供应和需求状况，高峰时段需求增多时，由于车辆的供给是固定的(一定时间和范围内，出租车的数量以及速度相对稳定)，就会造成供需的失衡，如果采用动态定价，供需将会达到新的平衡。

与传统出租车定价模型相同，下列的模型建立中也暂不考虑燃油费、夜间附加费、空返费以及低速费等因素。

2.1 动态定价模型的建立

建立一个多服务台排队系统模型(M/M/K)，来模拟乘客通过打车软件平台使用出租车服务的情形，如图1所示。

图1 打车软件参与下出租车排队服务模型

为了方便计算，只讨论进入稳定分布的排队模型，模型参数如下：

pn=P{N=n}(n=0，1，2，…)表示系统达到平稳状态后队长N的概率分布；

K为服务台数量，即出租车数量；

μn为系统处于状态n时出租车平均服务率，即单位时间内可以服务完的乘客数量，服务时间服从负指数分布，单个服务台的服务率记为μ，当n>K时，μn=Kμ；

λn为系统处于状态n时乘客的平均到达率，即单位时间内到达系统的平均乘客数量，服从泊松流；

λe记为乘客的有效到达率；

Q(t)记为t时刻排队人数；

T为系统处于稳定状态时乘客的逗留时间，均值记为W，即平均逗留时间；

Tq为系统处于稳定状态时乘客的排队等待时间，均值记为Wq。

首先考虑乘客不会损失的情况，假设乘客到达服从泊松过程，参数为λ，即实际输入率λe=λ。

假设平台的收益来源为出租车成交额的一定百分比，那么平台选择的动态定价策略p=p(Wt)要达到最大化平台的长期平均利润，我们可以得到平台t时刻的收入为λp(Wt)，公司最优化目标为

然而，实际情况中并不是所有到达的客户都会使用出租车服务，平常生活中我们如果觉得等的时间长，也会换成其他交通工具，或者放弃出行。因此，只有当乘客对服务定义的价值V大于系统给定的价格p时，才会加入队列。可以得出系统在t时刻乘客的有效到达率为

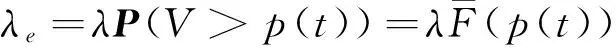
平台t时刻的收入可以表示为

公司最优化目标为

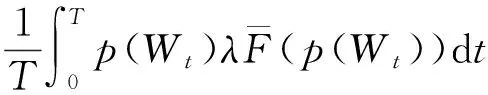
2.2 Matlab仿真

假设乘客意愿等待时间分布为0到1的均匀分布，即Wt～U[0，1]，当预计的等待时间超过乘客的意愿等待时间Wt时，乘客不再进入队列。

其他参数设置：总时间T=10；乘客到达率lambda=20；出租车的服务率μ=2；出租车数量K=10。

模拟结果如下：T时间内，共有176人发出需求，共计50人完成服务，总等待时间为12.916，总排队人数为0人次，总服务时间为13.51。

以等待时间为价格变量模型完成服务的乘客到达时间和离开时间，以及乘客等待时间和停留时间的模拟结果分别如图2和图3所示。

图2 以等待时间为价格变量模型完成 服务的乘客到达时间和离开时间

图3 以等待时间为价格变量模型完成 服务的乘客等待时间和停留时间

假设p(Wt)=10Wt+StC，C为常数，表示出租车行驶的基础成本。因此，由仿真模拟出的数据可得公司的收入为

可以看出，以等待时间为价格变量制定的价格策略，有效地减少了等待时间和排队人数，在提高公司收入的同时，也减少了乘客排队造成的时间浪费。

我们再来分析传统定价模型。假设传统的出租车运营效率、服务时间和上述仿真的一致(实际在有打车软件平台时，运营效率会有所提高，在这里暂不考虑这两者的区别)，价格函数无法得到观测并量化到排队造成的时间成本，因此只考虑行驶成本，即pi=C，所有支付意愿V超过C的乘客都会加入队列参与排队。假设所有乘客对于价格C都是可以接受的，而且对于等待时间的意愿和上一部分相同，服从0到1的均匀分布，即Wt～U[0，1]。如果乘客等待时间超过了他自己的等待意愿则退出队列。

参数设置：总时间T=10；乘客到达率lambda=20；出租车的服务率μ=2；出租车数量K=10。

模拟结果如下：共计211位乘客发出需求，45人完成了服务，总等待时间为92.64，总排队人数为0人次，总服务时间为13.78。

传统模式静态定价下乘客到达时间和离开时间，以及乘客等待时间和停留时间的模拟结果分别如图4和图5所示。

图4 传统模式静态定价下乘客到达时间和离开时间

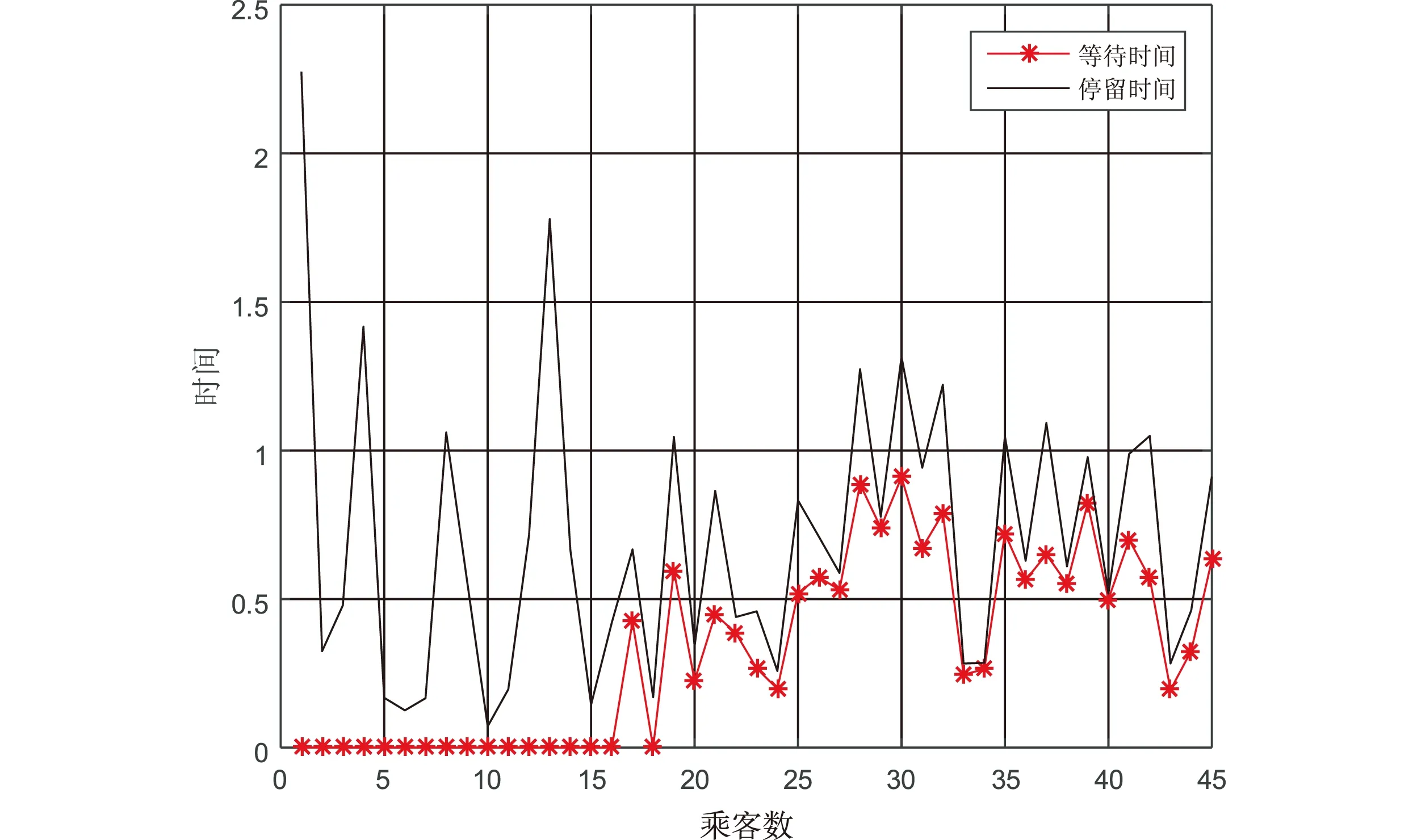
图5 传统模式静态定价下乘客等待时间和停留时间

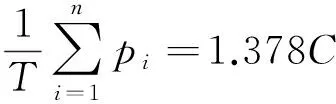
3 出租车合乘动态定价策略

出租车合乘是指出租车在有空位且乘客都同意的情况下，接载多方目的路线相同或不相同乘客的行为。从上世纪八十年代以来，美国、韩国、香港、台湾等多个国家和地区都实行了出租车合乘制度。研究指出，合乘可以有效缓解交通堵塞、降低能源排放、减少乘客支出，同时增加司机收入。北京最早于2014年出台了相关法规来规范出租车合乘业务，此后南京、哈尔滨等地也出台了相关的规定。然而，由于出租车在行驶过程中无法传递出可以拼车以及去往路线的信息，司机也无法收到潜在的有意愿完成合乘的乘客的信息，所以现有的合乘方式仍多为在同一地点，多方乘客完成拼车的传统模式。

随着科学技术的发展以及打车软件平台的广泛应用，完成合乘的技术条件越来越成熟，让车辆资源(行驶目的地、空余座位数量等信息)实现了深度可视性——乘客在上车时在平台上提交是否愿意拼车、出租车剩余座位以及目的地，如果其他乘客同意拼车，且车内座位满足、行驶路线有一定重合，则其他乘客就可以通过软件平台预订到该车，完成合乘。

3.1 现有出租车合乘定价策略

3.1.1 北京

北京市规定，两位及两位以上乘客在同一时间相同地点搭乘同一辆出租车时，需在第一位乘客同意，且总绕行距离不超过两公里的前提下，才可以合乘。计费方式为：如果下车地点不同，则每位乘客各支付合乘出租车路段车费的60%；如果在同一地点下车，则乘客平摊费用，但出租车司机总收费金额不应小于计价器的金额。

3.1.2 南京

《南京市出租车汽车营运服务管理规定》说明，合乘需要满足两个条件，同北京类似，即需第一位乘客同意合乘以及多位乘客顺路。计费方式也同北京相似，按合乘路段的里程每位乘客支付70%的费用。

3.1.3 福州

福州市允许出租车按照规定合乘，但前提条件是需在乘客双方皆同意合乘的情况下。计费方式为：收取每位乘客合乘路段60%的费用，乘客几人平均分摊燃油附加费。

3.1.4 哈尔滨

《哈尔滨市城市出租汽车客运管理条例》规定，在乘客同意搭载他人的情况下可以合乘。出租车司机与乘客商议决定最终的合乘费用和票据。

3.1.5 重庆

乘客在合乘路段支付80%的费用，单独乘坐出租车的里程，单独支付相关费用。

3.1.6 烟台

《烟台市出租车运价收费标准》规定，合乘乘客支付在下车地点计价器显示的收费金额的70%，即每位乘客支付总费用的70%。

通过上述城市的规定可以看出，现行的合乘规定多为同地点同时刻上车的情形，合乘路段费用按传统静态计费方式的比例进行分摊。上述规定的适用范围小，可操作性差，不具有普遍实施而改善城市交通状况、减少排放、提高收益的能力。因此，接下来我们将基于上一小节的动态定价策略，制定合乘模式的动态定价策略。

3.2 出租车合乘动态定价策略

和前面定价策略不同的是，合乘时出租车可以同时服务多名乘客，不同乘客的公共时间发生的公共费用需要分摊。假设乘客都是单人出现的，一个出租车可以供两名彼此陌生的乘客同时使用。乘客全部可以接受合乘模式。这相当于可利用的出租车座位数×2，单个出租车座位的服务率记为μ。此外，每个乘客支付的单位时间行驶成本为C。

公司t时刻的收入可以表示为

公司最优化目标为

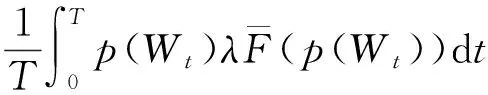
仍采用Matlab程序来进行仿真，参数设置如下：Wt～U[0，1]；总时间T=10；乘客到达率lambda=20；出租车的服务率μ=2；出租车可利用座位数K=20。

模拟结果如下：T时间内，共计205位乘客发出需求，90人完成了服务，总等待时间为17.16，总排队人数为0人次，总服务时间为28.9。

动态定价下合乘模式乘客到达时间和离开时间，以及乘客等待时间和停留时间的模拟结果分别如图6和图7所示。

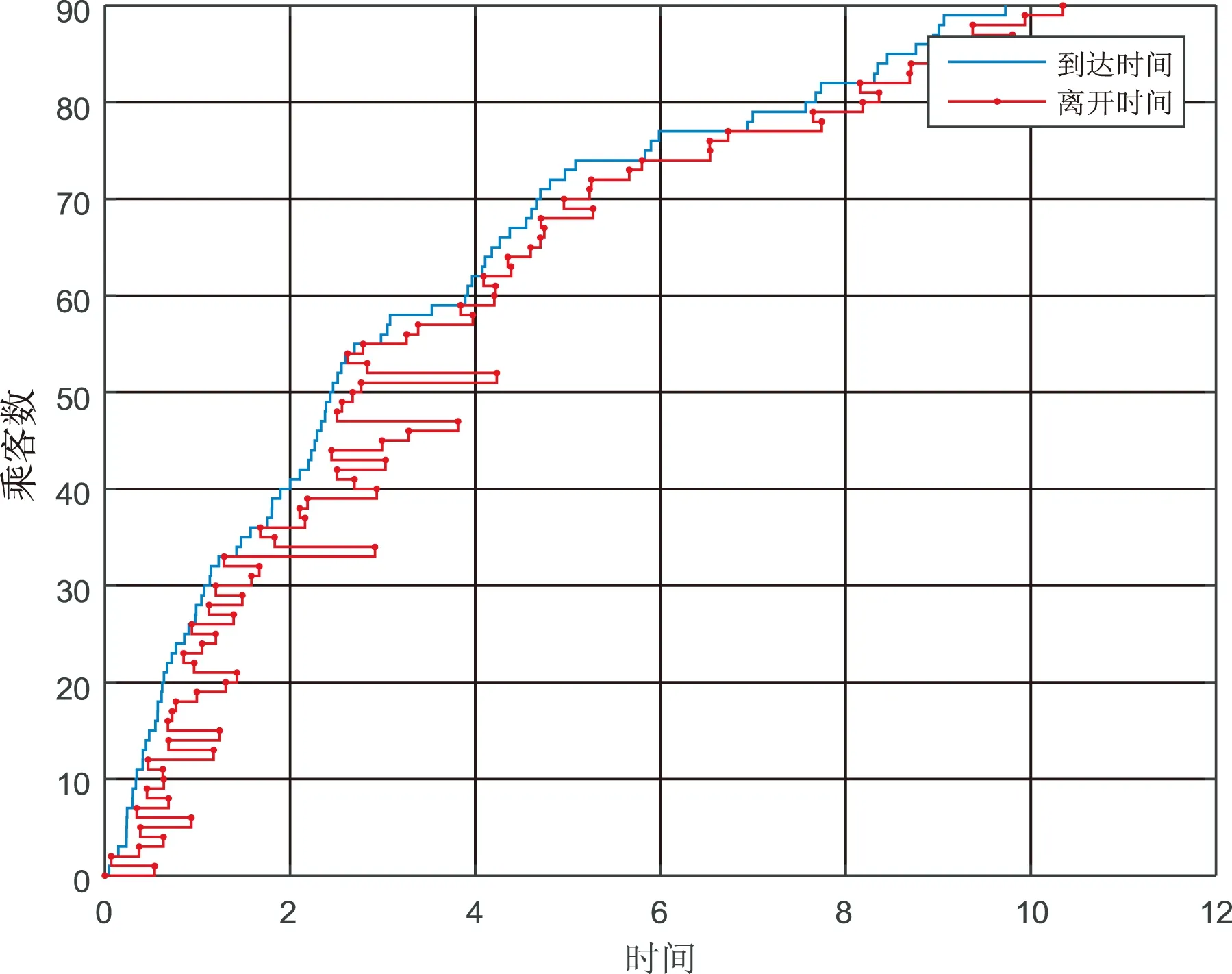
图6 动态定价下合乘模式乘客 到达时间和离开时间

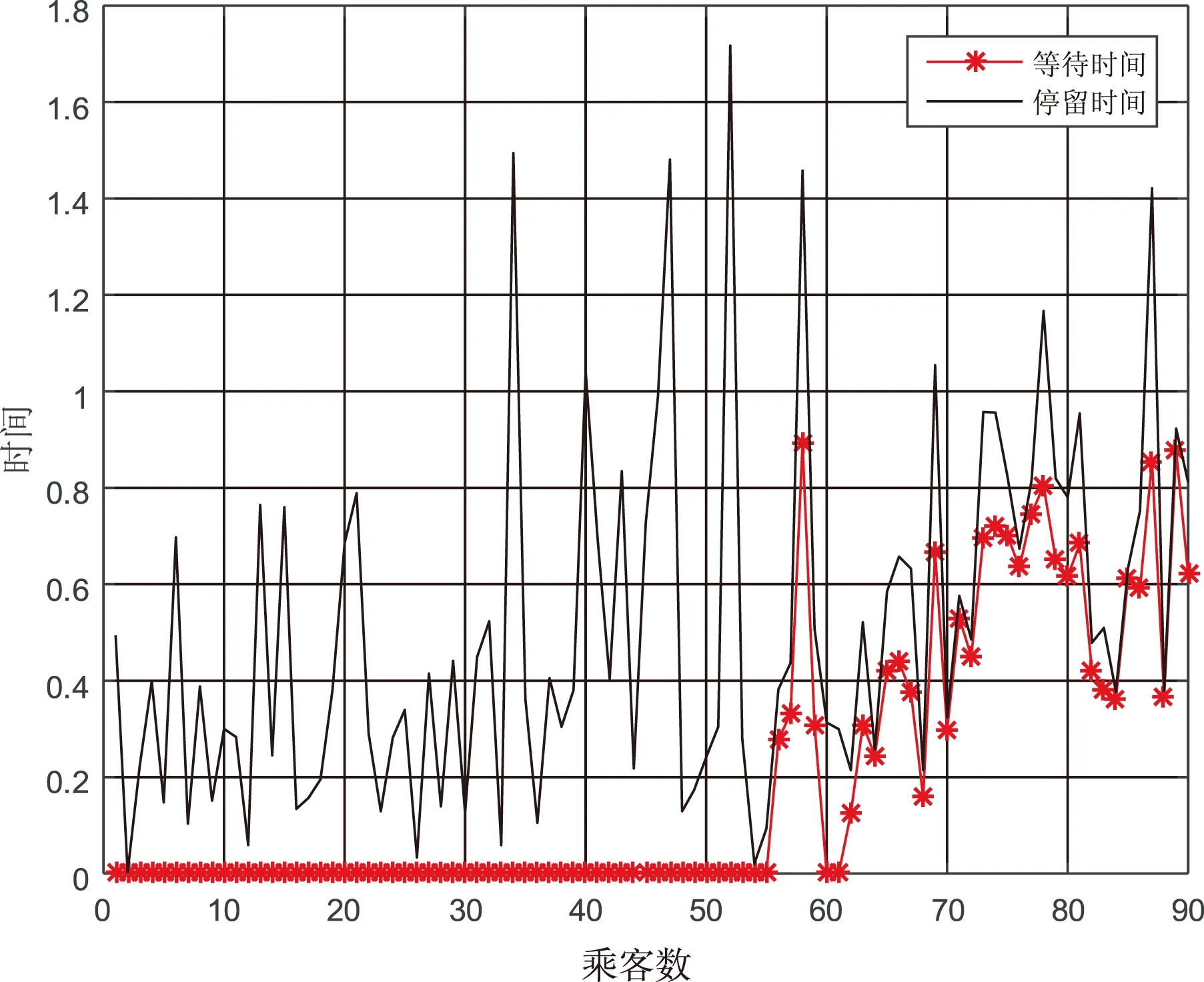
图7 动态定价下合乘模式乘客 等待时间和停留时间

可以看出参数相同的需求和服务率下，合乘对于出租车可用资源的释放有效地提升了运营效率，完成服务的乘客数接近翻番。假设p(Wt)=10Wt+C，由仿真模拟出的数据可得，公司该时段的平均收入为

4 结语

在对传统出租车定价模式以及部分城市合乘定价模式梳理的基础上，提出了将等待时间设为动态定价变量的定价策略。仿真结果表明，此定价策略可以提升公司收益，同时可减少社会资源(消费者时间)的浪费。

考虑到打车软件平台带来的出租车信息的深度可视，可以极大地促进合乘业务的实施，因此，在动态定价模型的基础上进行改进，建立了合乘模式的定价策略，通过Matlab仿真的结果可以得出，合乘模式可以有效提高资源的利用率，缓解日趋紧张的交通压力和越来越严峻的汽车尾气造成的环境污染问题。

[1] 张相斌，倪友谊.网格环境下制造资源优化配置的区间规划模型[J].数学的实践与认识，2012，24(6)：17-24.[2] 赵道致，杜其光，徐春明，等.物联网平台下企业之间制造资源转移策略[J].系统工程，2015，33(1)：88-93.

[3] 赵道致，杜其光，徐春明.物联网平台上两制造商间的制造能力共享策略[J].天津大学学报：社会科学版，2015，17(2)：97-102.

[4] 宗刚，李艳梅.出租车司机收入相对偏低的原因分析——以北京市为例[J].经济与管理研究，2008(5)：91-94.

[5] 石磊，李明忠.上海出租车驾驶员相对收入下降的原因分析[J].上海经济研究，2007(2)：8-10.

[6] 姜爱林.出租车集体罢运问题与出租车行业制度建设研究(上)[J].重庆工学院学报：社会科学版，2009，23(5)：59-65.

[7] 姜爱林.出租车集体罢运问题与出租车行业制度建设研究(下)[J].重庆工学院学报：社会科学版，2009，23(6)：22-29.

(责任编校：李秀荣)

A Research on the Dynamic Pricing Strategy of Taxi Software

ZHANG Jia-tong

(Department of Economics and Management， Tangshan University， Tangshan 063000， China)

The rapid development of science and technology and the popularity of smart phones have greatly improved information transfer. The taxi driver can， by the taxi software platform， conduct the real-time transmission of their service level， price， location and other information and passengers can also convey their offered price， location and other information by this platform. Under this background and based on the queuing theory， the author of this paper has designed a dynamic pricing model， which， compared with traditional models， can enhance the company’s revenue， and reduce social resources (e.g. consumer’s time). The car-pooling pricing strategy， based on the dynamic model， can effectively improve the utilization of resources and ease the tension of the traffic pressure.

taxi； dynamic pricing model； queuing theory

张佳彤(1968-)，女，河北唐山人，副教授，硕士，主要从事市场营销、物流管理研究。

F540.4

A

1672-349X(2016)06-0078-07

10.16160/j.cnki.tsxyxb.2016.06.020