磁场中矩形薄板的非线性内共振响应

李 晶

(唐山学院 基础教学部，河北 唐山 063000)



磁场中矩形薄板的非线性内共振响应

李 晶

(唐山学院 基础教学部，河北 唐山 063000)

给出了横向磁场作用下矩形薄板的磁弹性振动方程，针对一边固定、三边简支的矩形薄板，通过位移模态展开，并利用Galerkin法得到两自由度内共振非线性振动微分方程组。算例分析中，利用数值方法得到了系统内共振时两阶模态的时间历程响应图和相平面图，并分别讨论了系统初值及磁场强度对系统振动的影响。结果表明，系统呈现明显的非线性内共振特征。

导电矩形薄板；内共振；磁场

0 引言

矩形薄板结构在船舶制造、水利电力工程、空间站和航空航天领域被广泛应用，而这些结构通常处在机械荷载、电、磁等多种效应相互作用中，因此研究薄板在大变形情况下的复杂耦合动力学问题是十分必要的。许多学者在电磁弹性力学领域展开了研究，郑晓静等推导了导电铁磁梁式板的基本方程，讨论了电导率等参数以及支承条件对振动频率的影响[1]；胡宇达等给出了横向磁场环境中导电薄板的非线性磁弹性振动方程，分析了系统的复杂动力学问题，并建立了轴向运动导电薄板磁弹性耦合动力学理论模型[2-3]。近些年，随着现代非线性动力学理论的发展及数值计算手段的不断提高，许多学者利用平均法、多尺度法、摄动法、多元L-P法等解析方法研究了系统的非线性振动、局部和全局分岔及混沌动力学。Anlas等在1∶1内共振和横向简谐激励情况下，利用多尺度法研究了简支矩形金属板的非线性振动[4]；Tekin等运用多重尺度法研究了具有三次非线性项的多阶梯梁的3∶1内共振及稳定性问题[5]。本文将针对横向恒定磁场环境中一边固定、三边简支的矩形导电薄板，给出非线性磁弹性振动微分方程，采用伽辽金法得到矩形薄板无量纲化的达芬型非线性振动微分方程组，并利用数值方法分析其内共振特性。

1 一边固定、三边简支矩形板的振动微分方程

图1为横向恒定磁场B0(0，0，B0z)环境中的一矩形薄板。

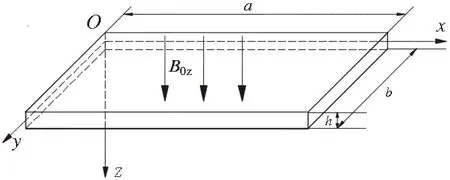
图1 横向恒定磁场中的矩形薄板

薄板沿x方向和y方向的几何尺寸分别为a和b，板厚为h，不受外激励作用，考虑机械场与电磁场的相互耦合作用，根据虚功原理，只考虑横向变形，并将中面内力、弯曲内力、电磁力矩相应的表达式[6]代入振动方程[7]中，忽略转动惯性力的影响，可得到横向磁场中矩形薄板关于挠度w的非线性磁弹性振动微分方程：

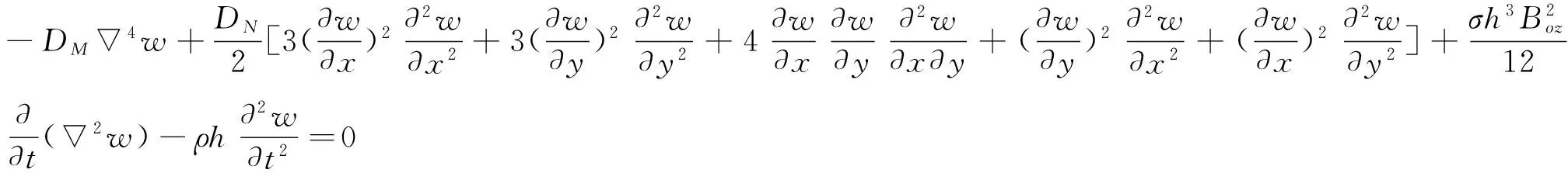
(1)

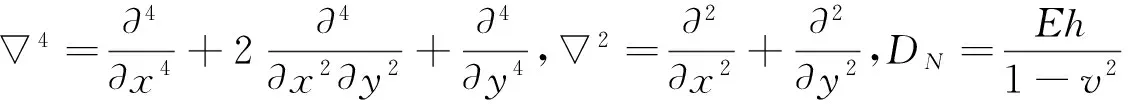
对于一边固定、三边简支的矩形薄板，边界条件为：

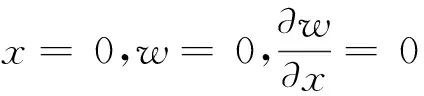
(2)

考虑系统前两阶模态，若系统二阶模态的固有频率近似等于一阶模态固有频率的3倍，可发生1∶3内共振。采用分离变量法，把时间变量和空间变量进行分离，设满足边界条件的位移解为：

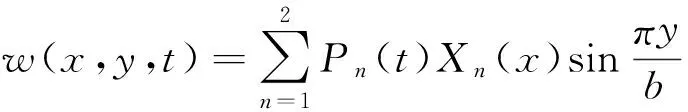
(3)

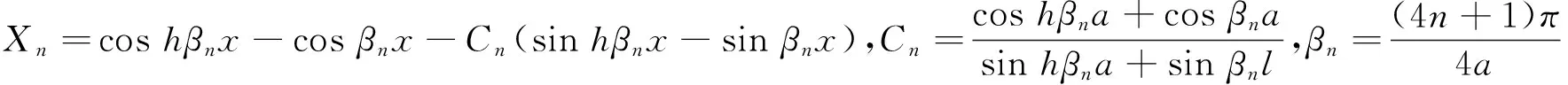
将位移函数(3)代入式(1)中，采用伽辽金法进行积分，并进行简化整理，得到矩形薄板无量纲化的横向振动微分方程组：

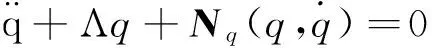
(4)

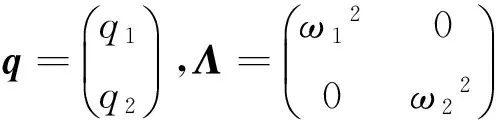
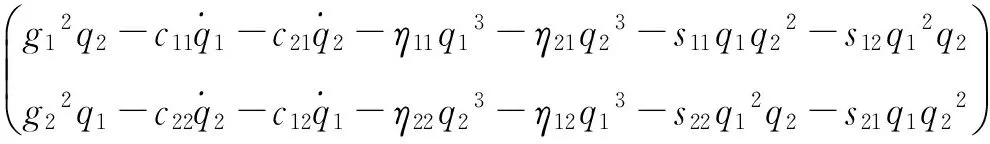
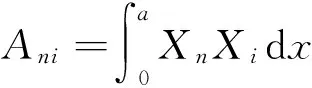
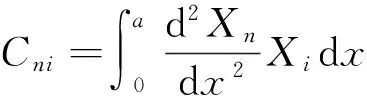
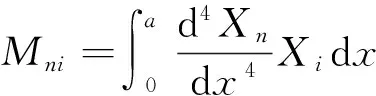
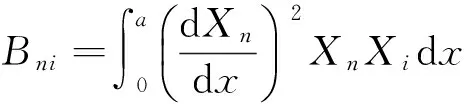
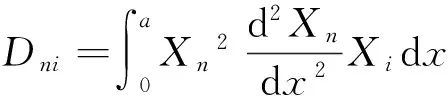
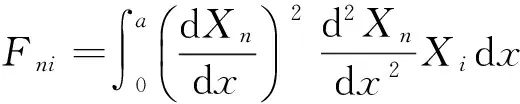
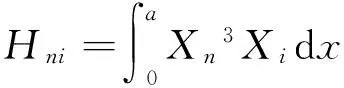
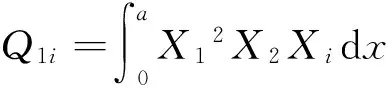
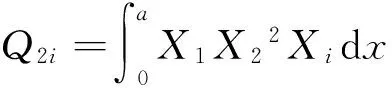
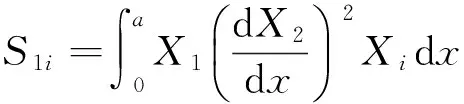
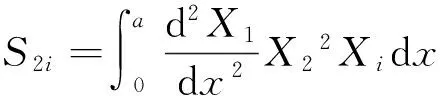
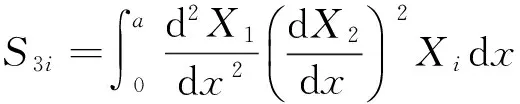
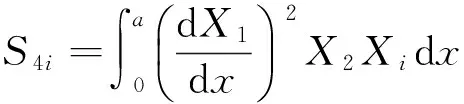
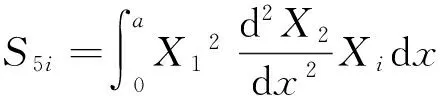
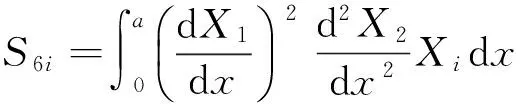
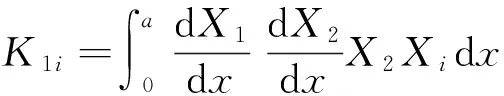
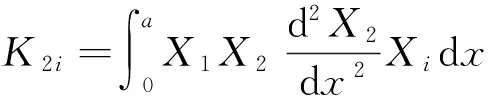
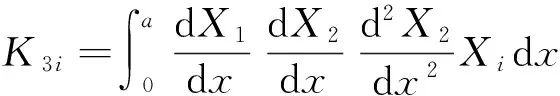
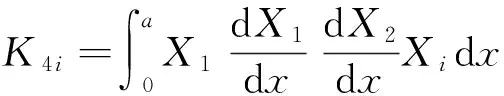
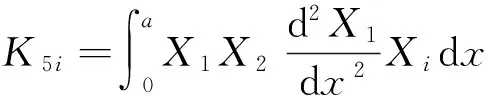
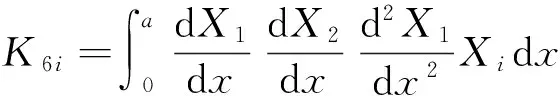
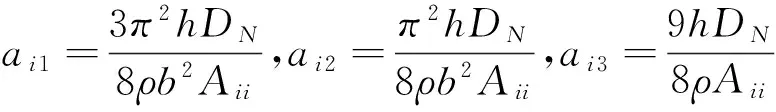
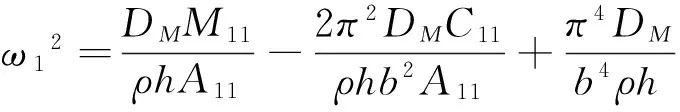
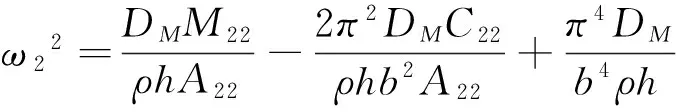
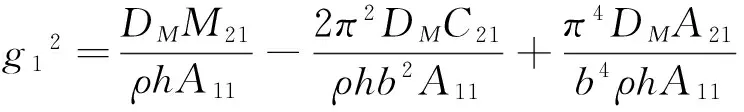
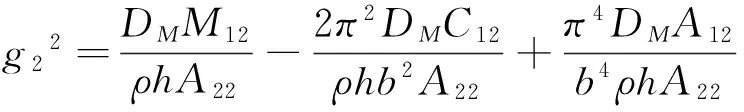
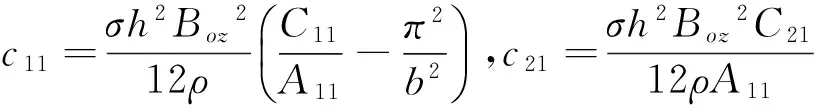
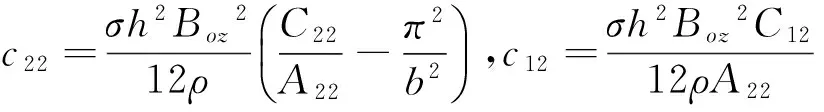
ηni=ai1Bni+ai2Dni+ai3Fni+ai4Hni，

si1=ai1(S1i+2K1i)+ai2(S2i+2K2i)+ai3(S3i+2K3i)-3ai4Q1i，

si2=ai1(S4i+2K4i)+ai2(S5i+2K5i)+ai3(S6i+2K6i)-3ai4Q2i，(i=1，2；n=1，2)。

所研究模型的一阶模态的固有频率和二阶模态的固有频率之间满足ω2≈3ω1的关系，为了讨论系统的内共振响应特性，直接对矩形薄板的横向振动微分方程组进行求解。

2 算例分析

对于处于横向恒定磁场中的铝制矩形导电薄板，给定主要参数：电导率σ=3.63×107(Ω·m)-1，密度ρ=2 670 kg/m3，泊松系数v=0.34，弹性模量E=71 GPa，板长b=1.2 m，板宽a=0.6 m，厚度h=6 mm。对于所给算例，利用Matlab对无量纲化的振动微分方程组(4)进行数值求解。

当磁场强度为零时阻尼项为零，系统做自由振动，图2为系统内共振响应图，分别给出了一阶模态、二阶模态随时间变化的曲线图以及一阶模态和二阶模态的相图。可以看出一阶模态和二阶模态均未衰减，仍做周期运动，且二阶模态的振动频率约为一阶模态振动频率的3倍。但此时的系统响应与单自由度系统自由振动下的响应有明显区别，原因就在于此时系统产生了内共振现象，两阶模态间存在着能量的交换。

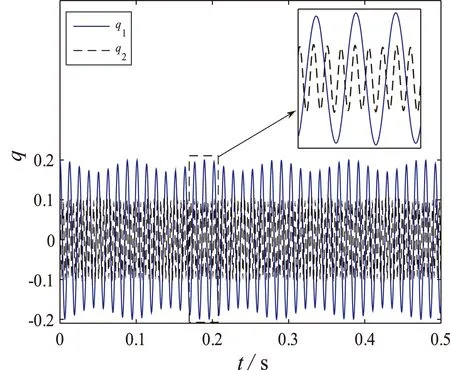
(a)时程图

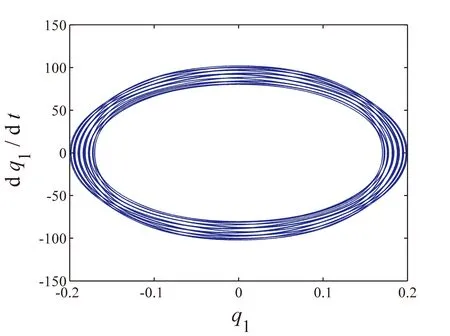
(b)一阶模态相图

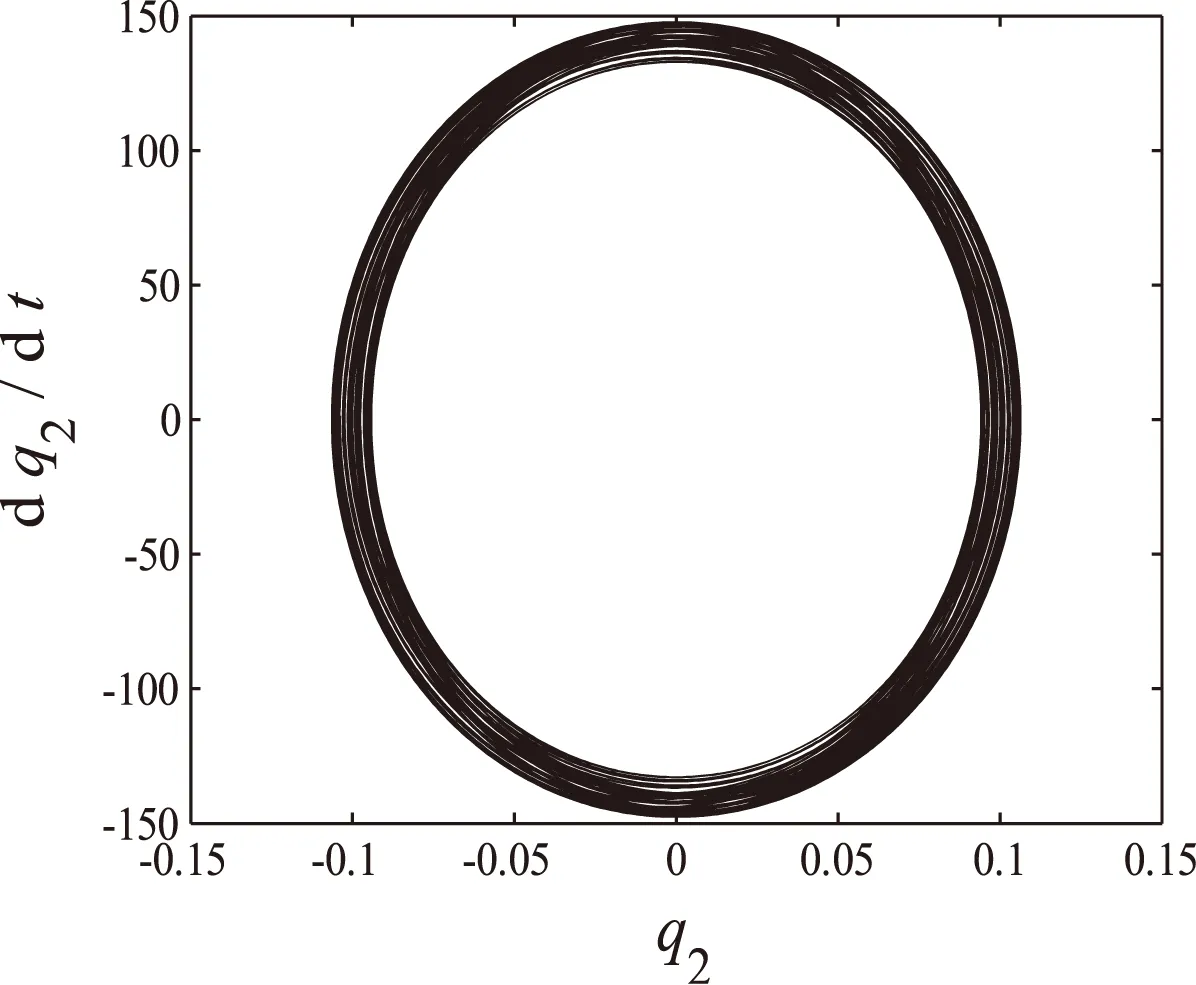
(c)二阶模态相图图2 系统内共振响应图

图3是将一阶模态和二阶模态振动的极大值找到，绘制出的极值随时间变化的曲线关系图。从图中可以看出，一阶模态和二阶模态在振动过程中确实出现了相互耦合的现象，说明系统产生了明显的内共振现象。

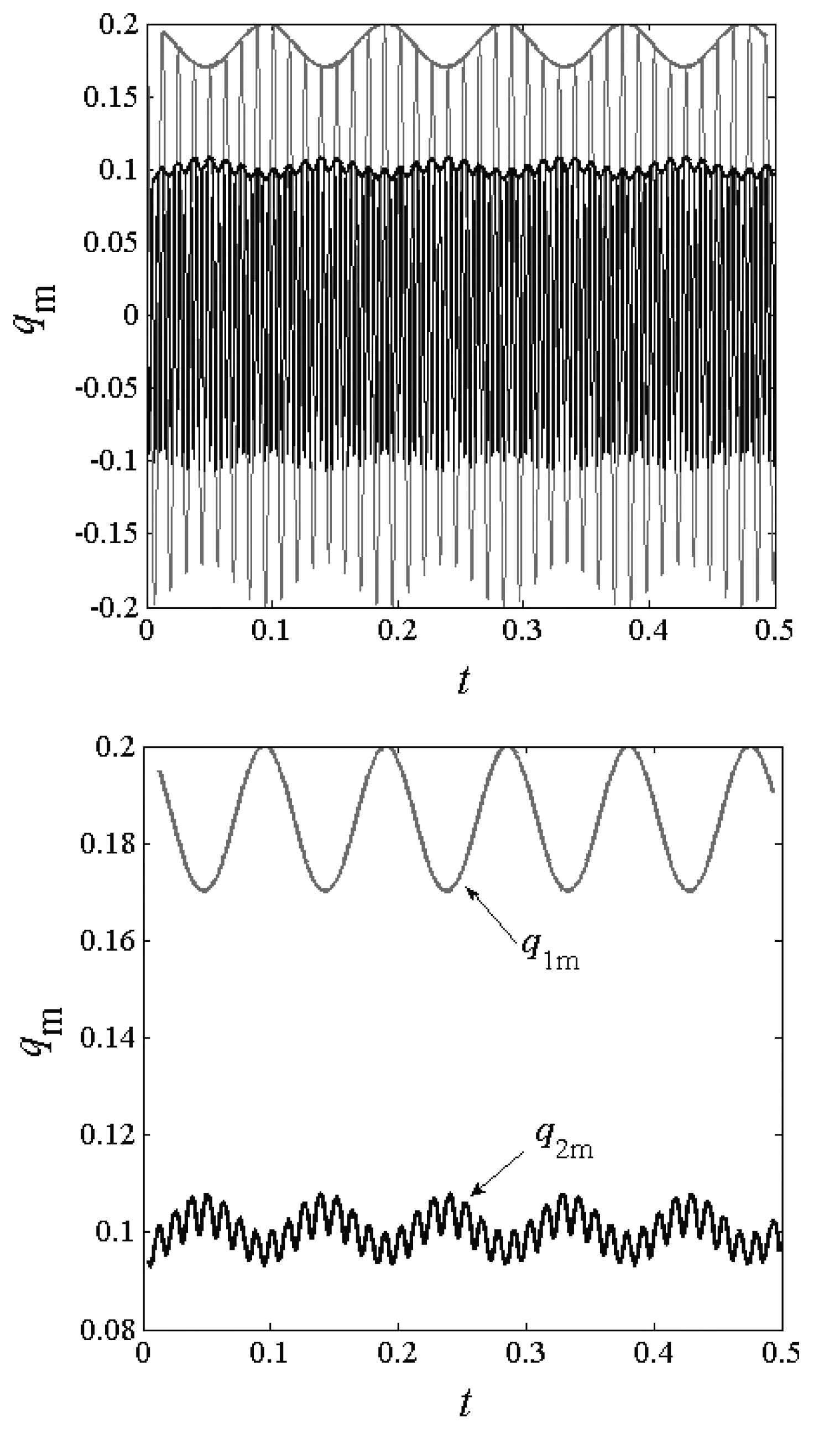
图3 模态极值随时间变化的曲线图

对于有阻尼系统，采用数值方法分析系统发生内共振时前两阶振动模态的变化特性，讨论磁场强度对模态振幅的影响。

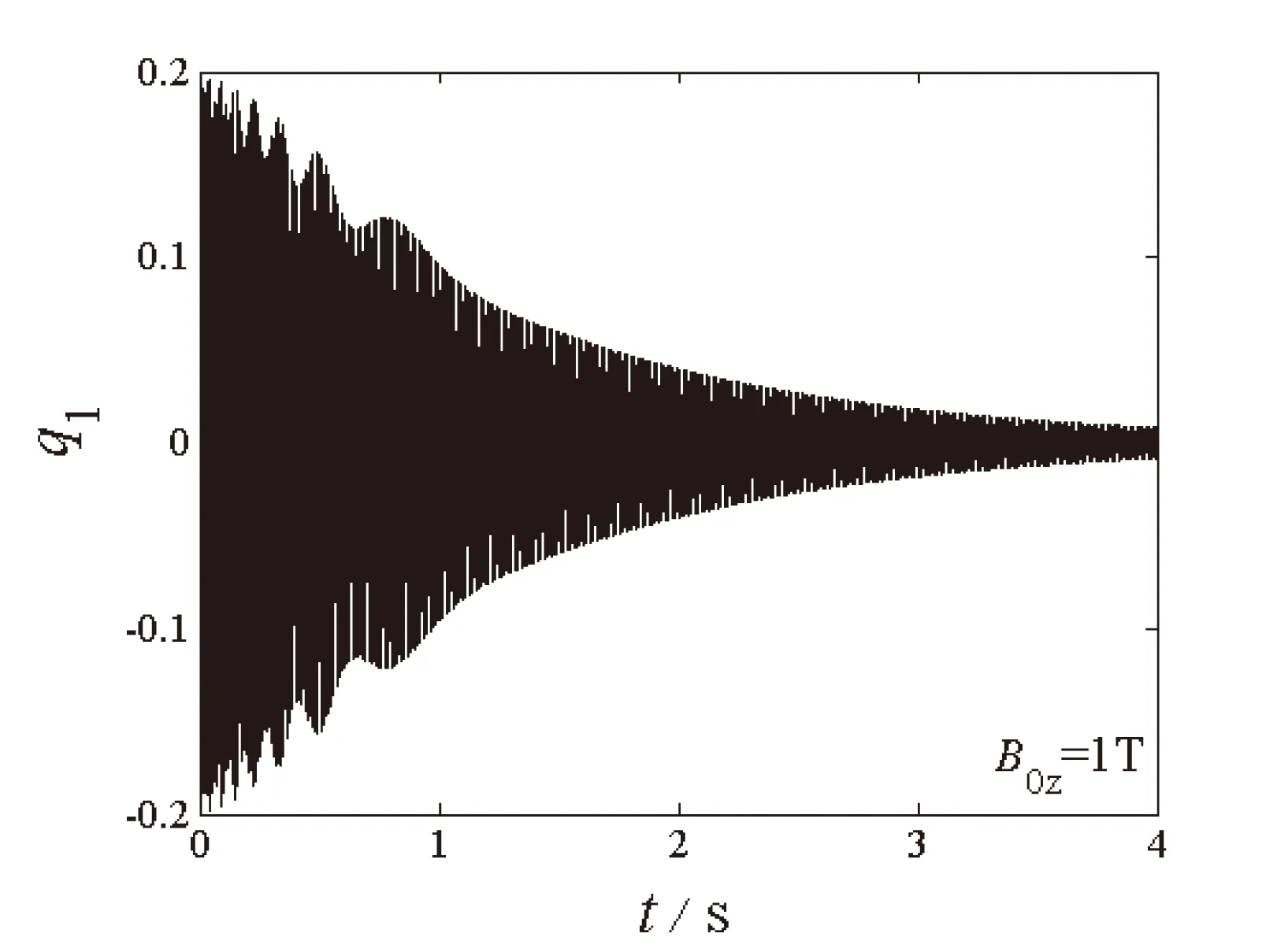
(a)一阶模态时程图

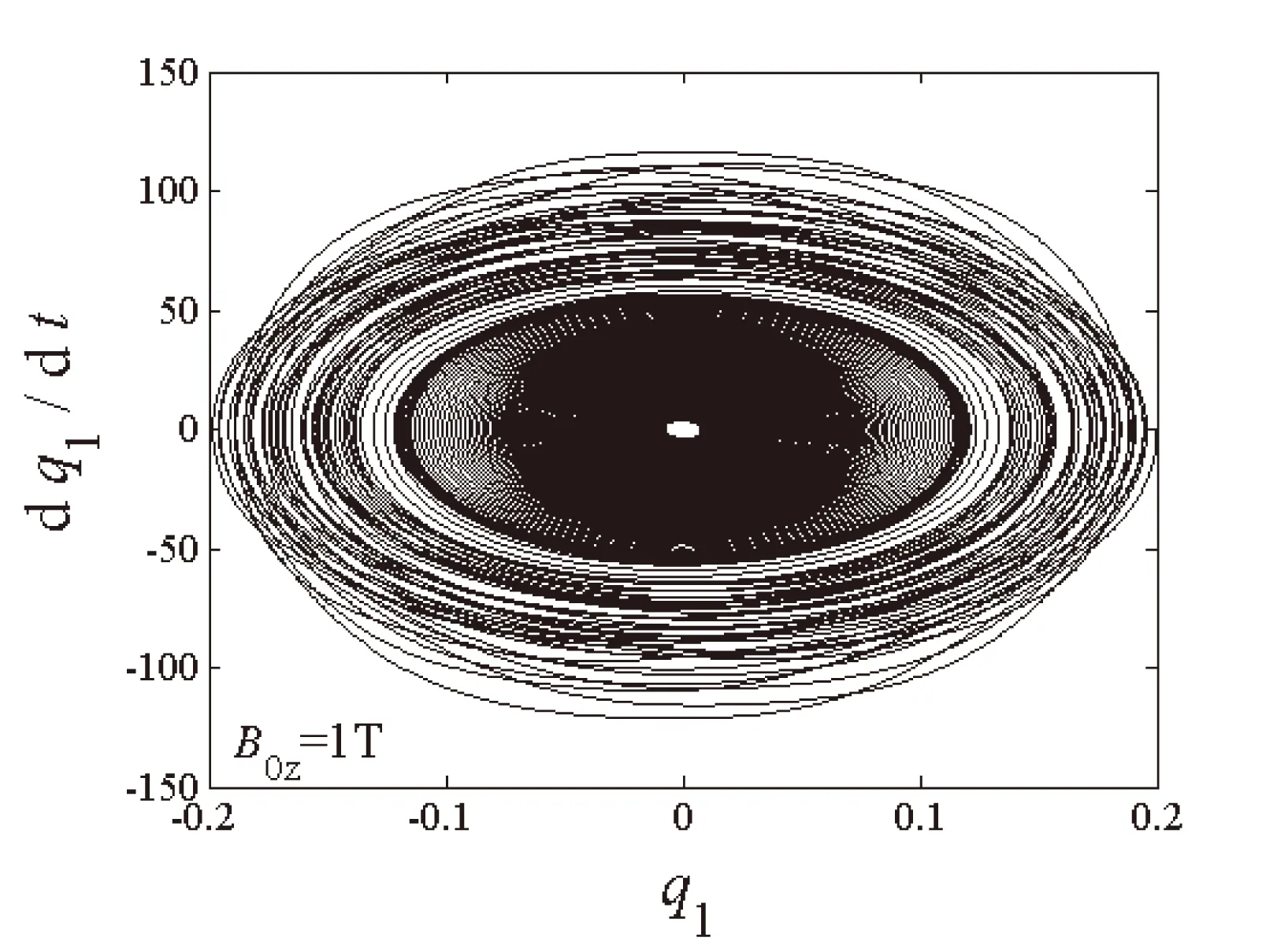
(b)一阶模态相平面图

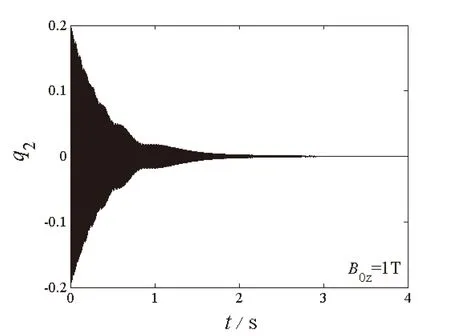
(c)二阶模态时程图

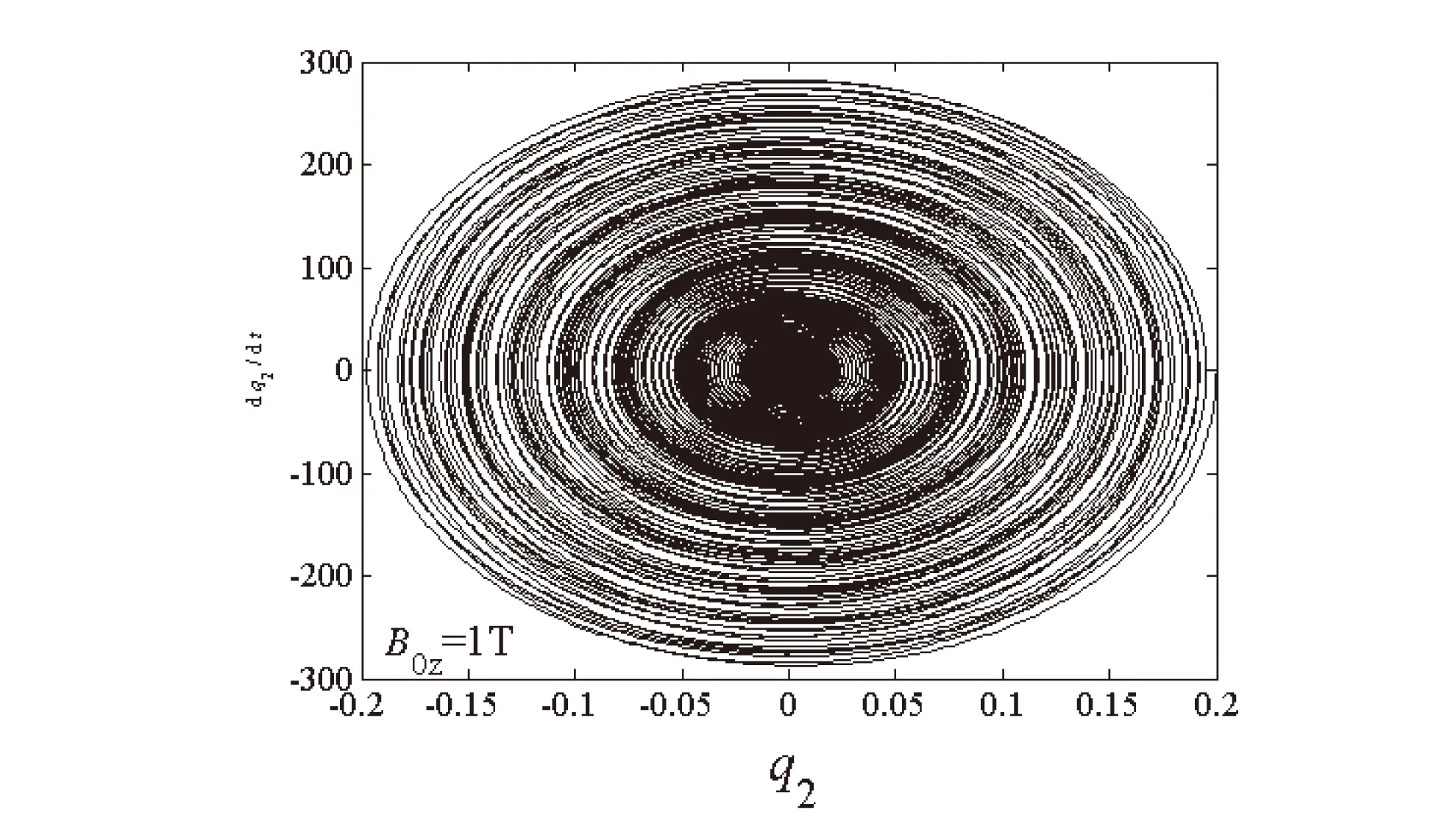
(d)二阶模态相平面图图4 系统内共振响应图(B0z=1 T)

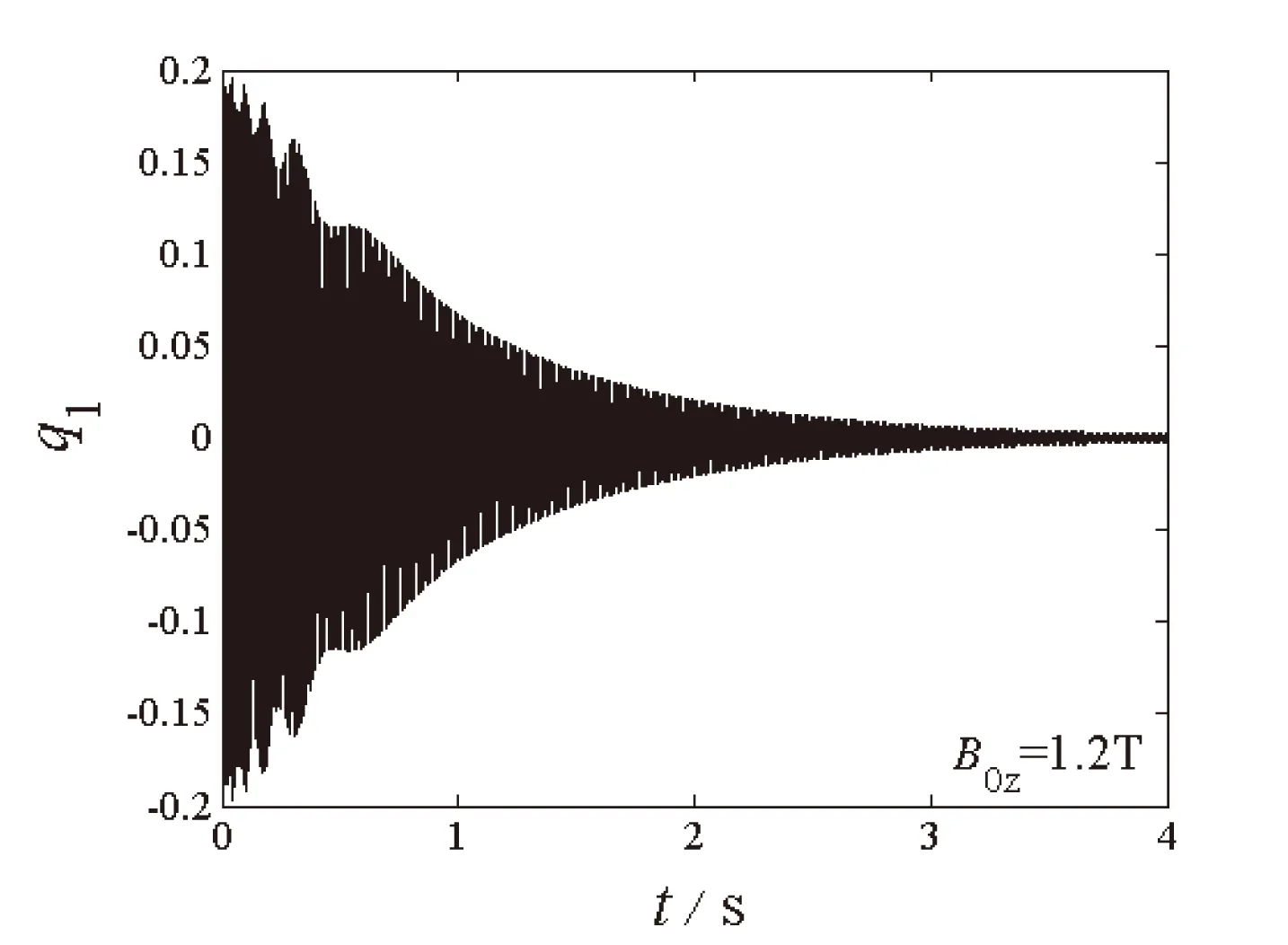
(a)一阶模态时程图

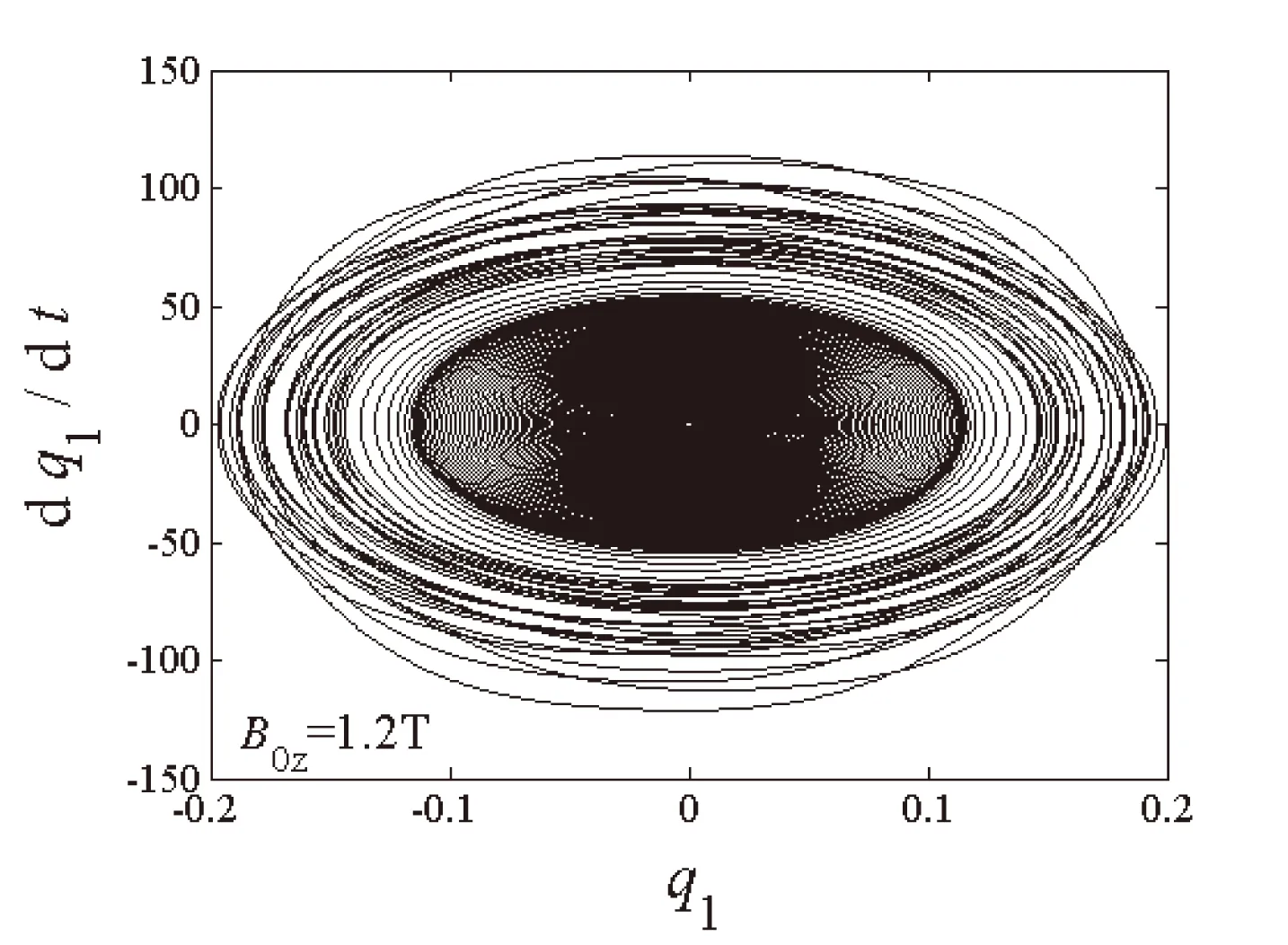
(b)一阶模态相平面图

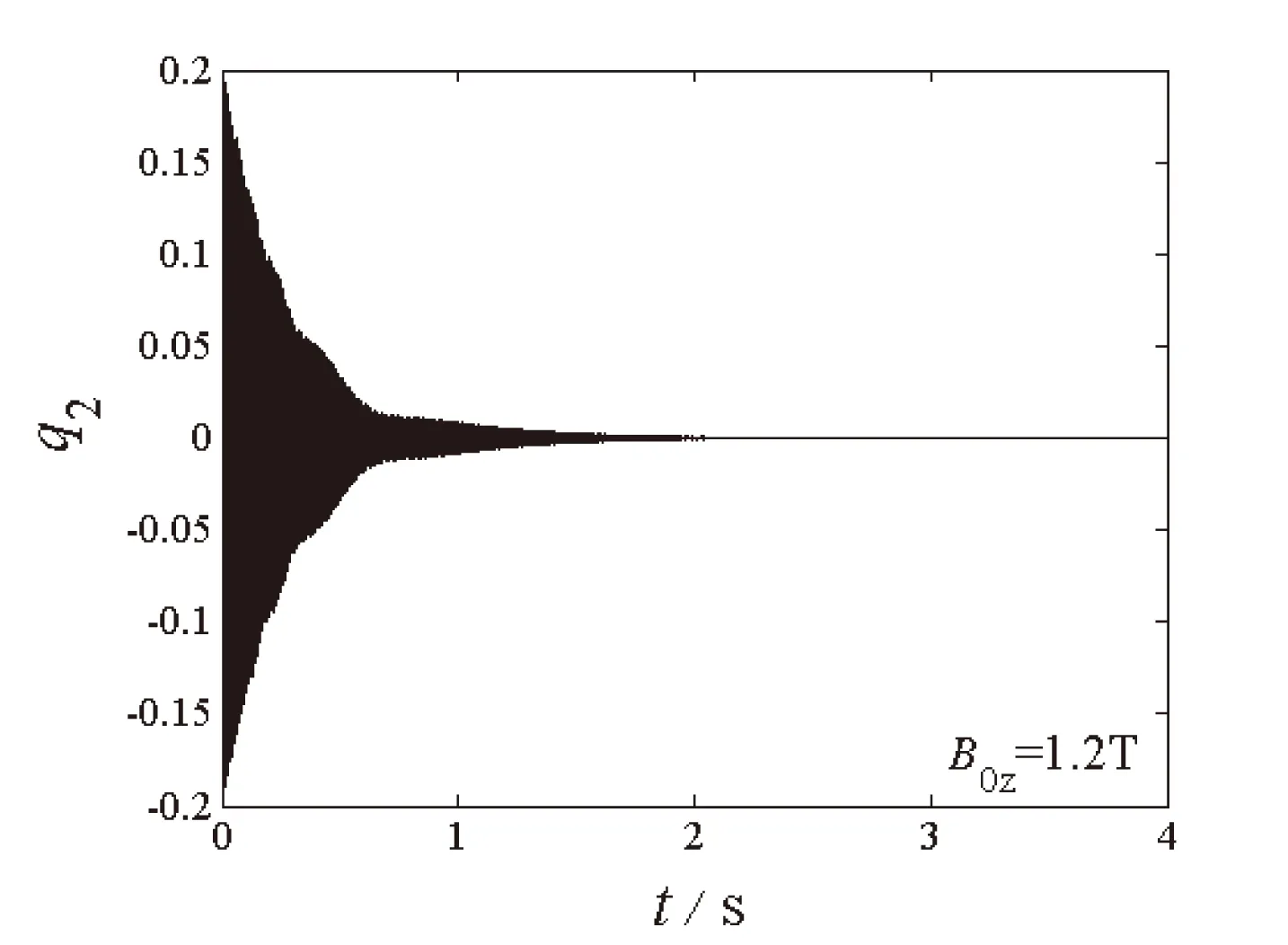
(c)二阶模态时程图

(d)二阶模态相平面图图5 系统内共振响应图(B0z=1.2 T)

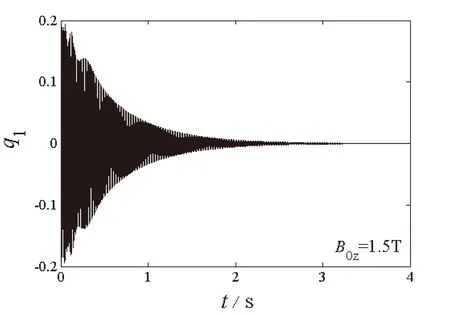
(a)一阶模态时程图

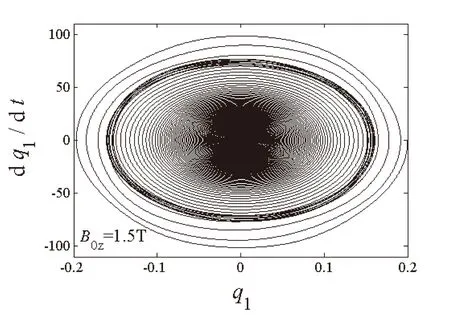
(b)一阶模态相平面图

图4至图6给出了自由振动系统在给定初始值q10=q20=0.2时，不同磁场强度下两阶模态q1和q2随时间的变化图和相平面图。可以看出在电磁场环境中，阻尼项取决于磁场强度，系统两阶模态在磁场作用下均呈现自由衰减态势，并逐渐衰减为零，一、二阶模态在衰减过程中仍然存在着能量交换，且二阶模态的衰减速度快于一阶模态的衰减速度。磁场强度越大，两阶模态的时程和相平面的收敛速度越快。

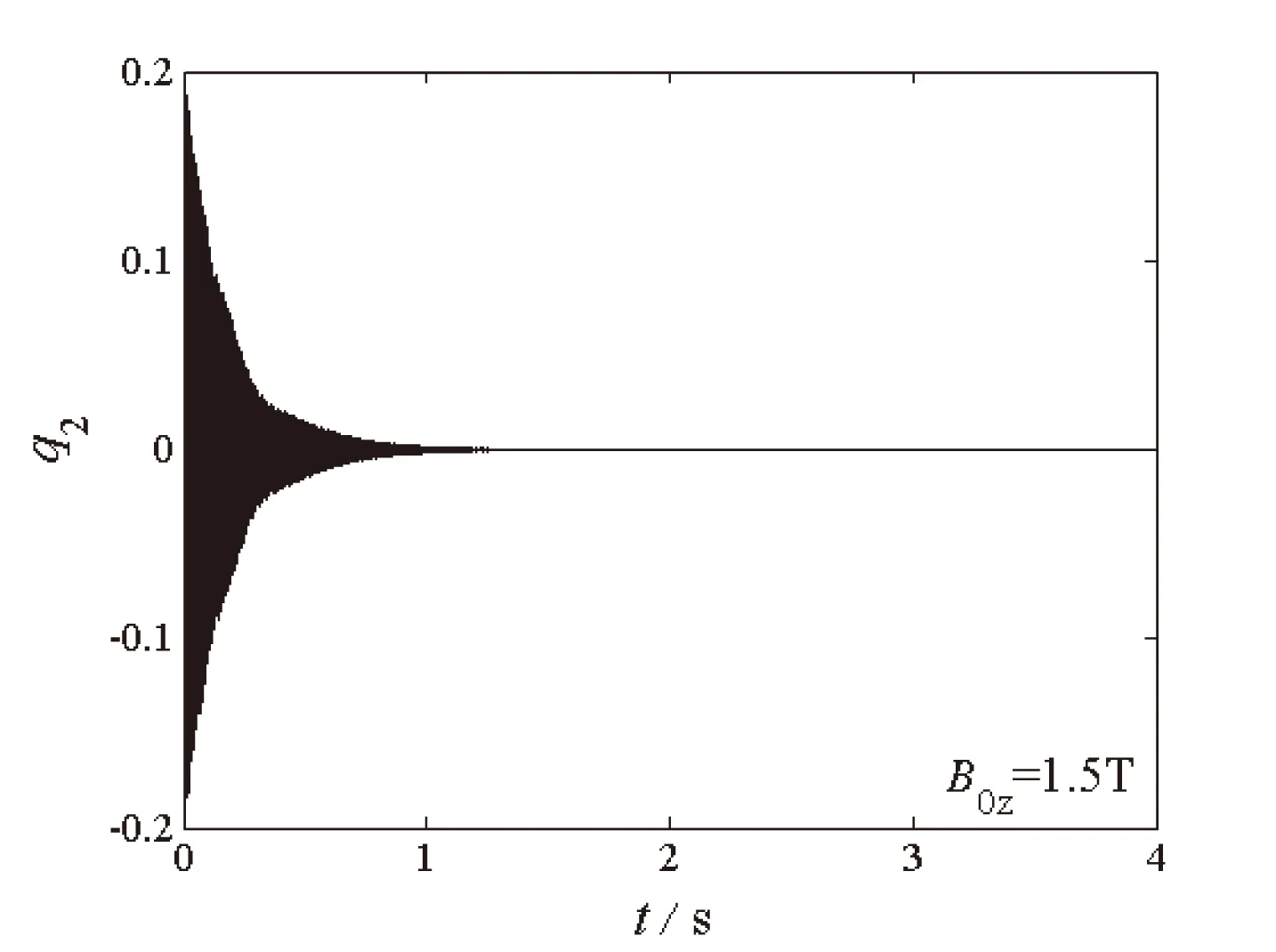
(c)二阶模态时程图

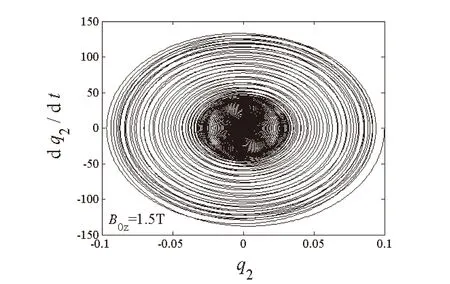
(d)二阶模态相平面图图6 系统内共振响应图(B0z=1.5 T)

3 结论

本文根据横向磁场中矩形导电薄板的磁弹性振动方程导出了矩形薄板无量纲化的横向振动微分方程组。通过数值算例，利用数值方法求解了系统的内共振问题。结果表明：系统能量在两个振动模态之间不断地交换，体现出1∶3内共振特性。有阻尼时，系统的前两阶振动模态呈现出耦合衰减的趋势且随磁场强度的增强而加速衰减。

[1] 郑晓静，刘信恩.铁磁导电梁式板在横向均匀磁场中的

动力特性分析[J].固体力学学报，2000，21(3)：243-250.

[2]HuYD，LiJ.Themagneto-elasticsubharmonicresonanceofcurrent-conductingthinplateinmagneticfiled[J].JournalofSoundandVibration，2009，319(3-5)：1107-1120.

[3] 胡宇达.轴向运动导电薄板磁弹性耦合动力学理论模型[J].固体力学学报，2013，34(4)：417-425.

[4]AnlasG，ElbeyliO.Nonlinearvibrationsofasimplysupportedrectangularmetallicplatesubjectedtotransverseharmonicexcitationinthepresenceofaone-to-oneinternalresonance[J].NonlinearDynamics，2002，30(1)：1-28.

[6] 胡宇达.传导薄板在磁场环境中的非线性磁弹性振动问题[J].工程力学，2001，18(4)：89-94.

[7] Амбарцумян С А，Багдасарян Г Е，Белубекян М В.Магнитоупругость тонких оболочек и пластин[M].Москва：Наука，1977：146-199.

(责任编校：夏玉玲)

On the Nonlinear Internal Resonance of Rectangular Thin Plate in Magnetic Field

LI Jing

(Department of Basic Science Teaching， Tangshan University， Tangshan 063000， China)

The author of this paper has deduced the magnetoelastic vibration equation of the rectangular thin plate in transverse magnetic field. With Galerkin and through displacement mode expansion， the author has also acquired the differential equations of the two-DOF internal resonance nonlinear vibration in relation to a rectangular thin plate with one side fixed and three other sides simply supported. The author has obtained the two-order mode time history response diagram and phase plan under the internal vibration of the system through the analysis of samples and with numerical method， and discussed the initial value of the system and the influence of magnetic field intensity on the vibration. The results show that the system exhibits the characteristics of obvious nonlinear internal resonance.

rectangular current-conducting thin plate； internal resonance； magnetic field

国家自然科学基金项目(11472239)；河北省自然科学基金资助项目(A2015105073)；唐山市科技计划项目(15130262a)

李晶(1981-)，女，河北唐山人，讲师，硕士，主要从事非线性磁弹性振动研究。

O322；O442

A

1672-349X(2016)06-0001-05

10.16160/j.cnki.tsxyxb.2016.06.001