变量惩罚效应在贝叶斯分位数回归模型的应用
郭俊峰
(厦门大学经济学院,福建厦门361005)
变量惩罚效应在贝叶斯分位数回归模型的应用
郭俊峰
(厦门大学经济学院,福建厦门361005)
尽管贝叶斯分位数回归方法能够有效克服经济金融数据的尖峰厚尾、结构突变等问题,充分借鉴已有研究成果信息,但是其并不能很好解决多维变量模型的维数灾难问题。为此,文章在贝叶斯分位数回归基础上,结合自适应Lasso变量惩罚作用,构建了基于MH抽样的自适应Lasso惩罚贝叶斯分位数回归模型。通过仿真模拟实验以及MCMC链条检验,证明上述模型具有优良拟合性质,尤其是在小样本情形下。
维数灾难;自适应Lasso惩罚;贝叶斯;分位数回归
0 引言
伴随着计算机技术和计量模型的发展,学者们开始将分位数回归(Quantile Regression,QR)方法运用于经济金融、卫生统计等领域的研究,它能够有效克服数据的尖峰厚尾以及结构突变等问题,还对极端异常值有很强的鲁棒性,因此该方法日益受到研究人员重视。分位数回归方法本身也不断扩展延伸,其中一个重要方向是与贝叶斯估计结合,通过不对称Laplace分布来构建贝叶斯分位数回归(Bayesian Quantile Regression,BQR)模型[1],从而有效利用以往研究成果信息、提高样本数据较少时的参数估计精度。
可是在多维变量模型中,BQR方法平等估计每个解释变量而不考虑变量作用显著与否,换句话说,BQR模型不能解决维数灾难问题,即使Tibshirani在1996年[2]提出了Lasso变量惩罚方法,也不能很好处理多维变量模型的维数灾难问题,因为该方法对所有自变量都施以相同惩罚,而这显然与不同自变量对因变量影响各异的规律相悖。
基于此,本文在贝叶斯分位数回归模型基础上,尝试着结合自适应Lasso变量(Adaptive Lasso)惩罚作用[3],对不同自变量给予不同惩罚系数。经过理论推导,最终构建了基于MH抽样的自适应Lasso惩罚贝叶斯分位数回归(Adaptive Lasso Bayesian Quantile Regression,ALBQR)模型。仿真模拟分析表明,相比于0LS模型、QR模型及BQR模型,ALBQR模型有更好的拟合效果。
1 模型构建与贝叶斯分析推导
1.1贝叶斯分位数回归BQR模型
Koenker和Bassett(1978)[4]率先提出分位数回归方法。给定自变量X信息后,Y的第τ分位数水平线性条件分位数模型表达式为

也就是
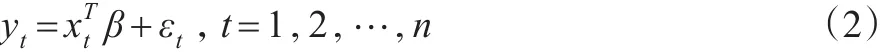

得到QR模型系数β的估计值,其中ρτ(u)=u(τ-I(u为示性函数。
实际研究中,我们往往还可以参照以前相关成果。然而,普通QR模型并没有借鉴这些经验,所以下面对该模型进行贝叶斯分析推导,构建贝叶斯分位数回归BQR模型。为了将贝叶斯方法纳入到分位数回归框架,本文需要运用不对称拉普拉斯先验分布(Asymmetric Laplace Distribution,ALD)。给定,μ是位置参数,σ是尺度参数,p是偏度参数,那么其密度函数如下:
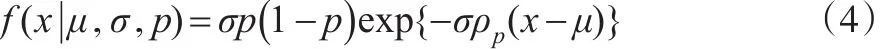
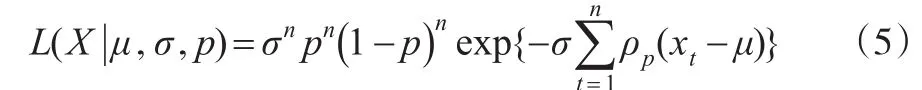
Tsionas(2003)[5]证明,如果x~ALD(μ,σ,p),那么x可以等价表示为:

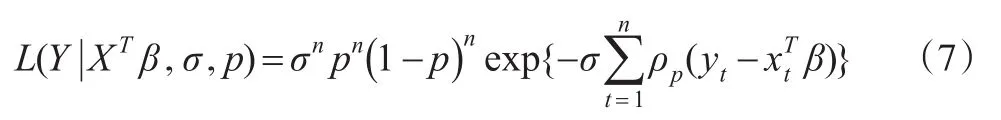
比较式(3)与式(7),看出极小化式(3)等价于极大化式(7),分位数水平τ等同于ALD分布的偏度系数P。根据式(6),将因变量yt表示成:

相应地,BQR模型的参数估计值为:
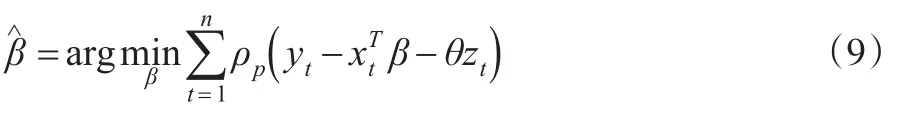
1.2带有变量惩罚效应的贝叶斯分位数回归模型
尽管BQR模型可以很好地解决数据的尖峰厚尾、结构突变等问题,也充分利用了已有先验信息。但在参数估计时,该方法却不加选择地平等对待每个解释变量。由于多维变量模型普遍存在“维数灾难”难题,所以Tibshirani(1996)[2]提出了Lasso变量惩罚方法。可是Lasso惩罚方法没有0 racle估计性质,其对所有变量的回归系数都施以相同惩罚。这显然与现实规律相违背。为此,对于BQR模型,我们借助自适应Lasso惩罚方法,通过选择适当权重,对不同变量给予不同惩罚系数,从而得到自适应Lasso惩罚贝叶斯分位数回归(Adaptive Lasso Bayesian Quantile Regression,ALBQR)模型,其具有0 racle性质的参数估计值为:
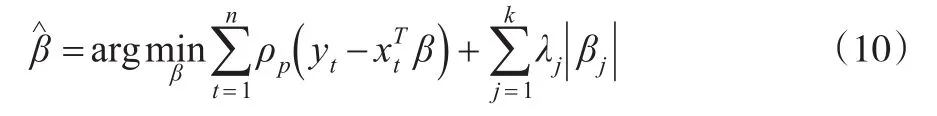
其中λj是非负的可变惩罚系数。
1.3ALBQR模型参数估计与算法设计
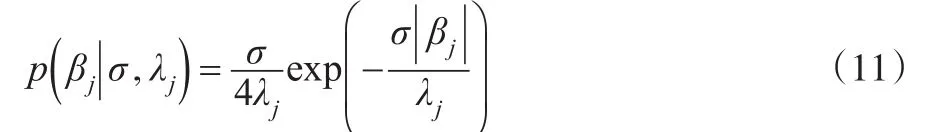
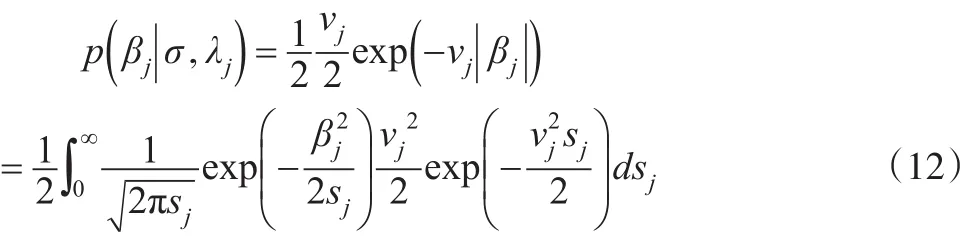
进而
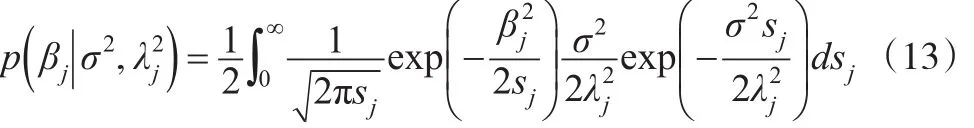

式(14)中,δ、ψ为超参数。综上所述,本文通过假设参数βj和误差项εt都服从ALD先验分布,并对参数βj施以可变惩罚作用参数先验分布分别为:
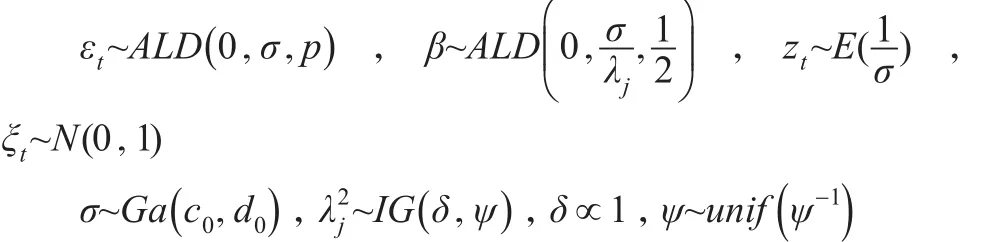
贝叶斯估计参数时,后验分布密度函数较难求解并且形式复杂,一般很难得到后验分布密度的明确表达式,所以只能借助模拟抽样技术。MCMC是一种简单有效的数值模拟计算方法,包括Gibbs抽样和MH抽样,Gibbs抽样本质是接受概率恒为1的MH抽样特例,本文用MH抽样算法来进行贝叶斯参数估计。MH抽样从建议分布q(θ,θ')中抽样得到候选样本θ',然后以概率a(θ,θ')决定是否接受由θ→θ',形成转移核p(θ,θ'),具体如下:

设第k步马尔可夫链的状态向量为θ(k),根据建议分布产生另一状态向量θ‘,然后随机从均匀分布U(0,1)中抽取a,如果就接受,否则θ(k+1)=θ。
2 仿真模拟分析
2.1数据来源
我们接下来进行仿真模拟,以检验ALBQR模型的合理性和优越性,尤其在小样本情形下。简单起见,设定123456为随机数种子,生成6个在不同区段的均匀分布变量,变量个数用N表示,本文取N为20、50及100。然后根据下列方程式生成因变量Y:
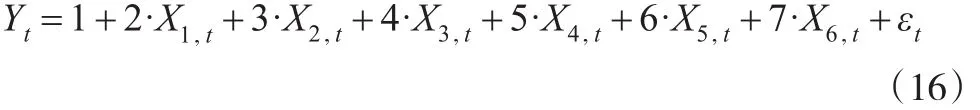
上式中,误差项εt被设为服从零均值、异方差的正态分布。很明显,对于7×N个模拟数据而言,式(16)就是多维变量模型回归方程,并且样本数量N也有大有小,因此这些数据符合仿真模拟的要求。
2.2仿真结果分析
假定ALBQR模型的先验参数σ~Gamma(0.001,0.001),步长是1。进行MH抽样50000次,预烧30000次,剩下数据用于估计上述6个模拟变量的系数。表1—表3分别提供了样本量N为20、50及100时的参数后验均值。为便于比较,我们还列出0L和BQR模型的相应结果。
根据表1至表3,我们发现如下规律:第一,普通最小二乘法0LS的参数估计值的确介于不同分位数水平的BQR(或者ALBQR)估计值之间,这是由于0LS方法估计的是条件均值方程,注重平均角度,而分位数模型通过变动分位数水平,还可以研究两端尾部极端情况下的变量关系,所以0LS能够挖掘出的信息量最少。第二,就同一模型来说,随着样本量N增大,所有估计值都越来越显著,这说明误差百分比逐渐降低,参数估计精度都得到提高。同时,0LS、BQR与ALBQR模型之间的估计精度差别也不断缩小。第三,在同一样本量下,0LS方法最不准确,相比而言,ALBQR的参数估计系数最接近各个模拟变量的真实值。尤其是在样本量很小(N=20)时,ALBQR模型的优势更加明显。
采用贝叶斯方法估计参数后,需要检验变量MCMC链条的收敛性,本文使用Geweke检验方法。限于篇幅,我们只列出样本量N为100时的MCMC链条(tau=0.25、0.5、0.75)收敛性判断结果。表4汇报了检验情况。
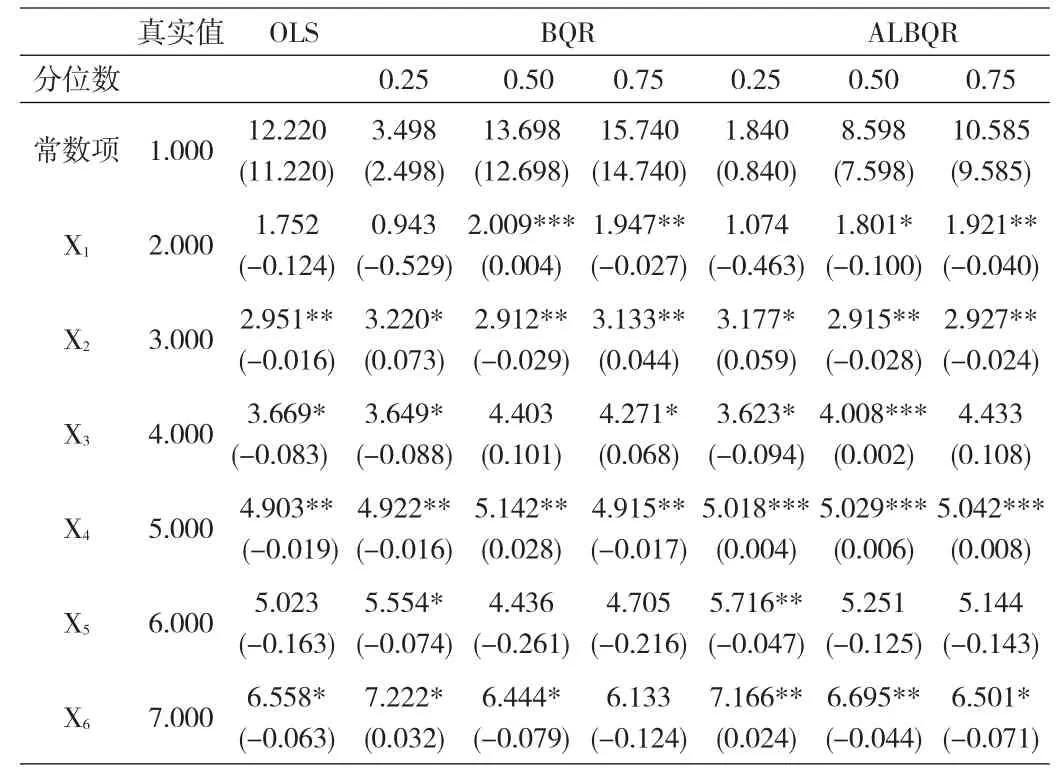
表1 仿真模拟结果(样本量N=20)
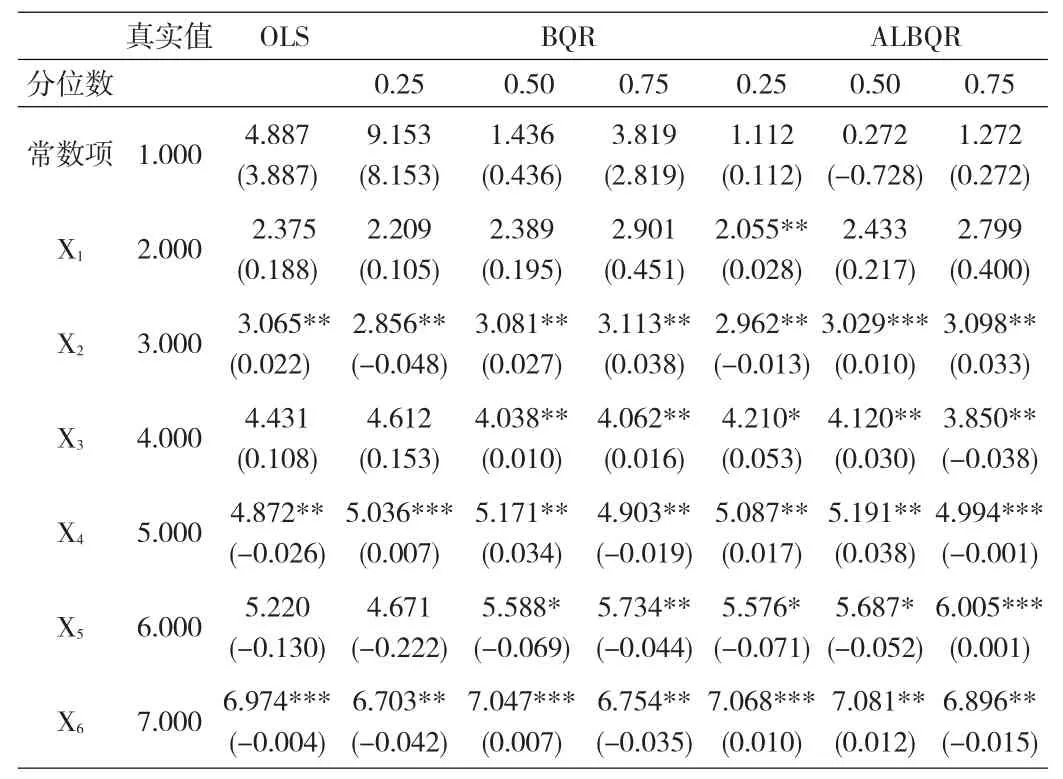
表2 仿真模拟结果(样本量N=50)
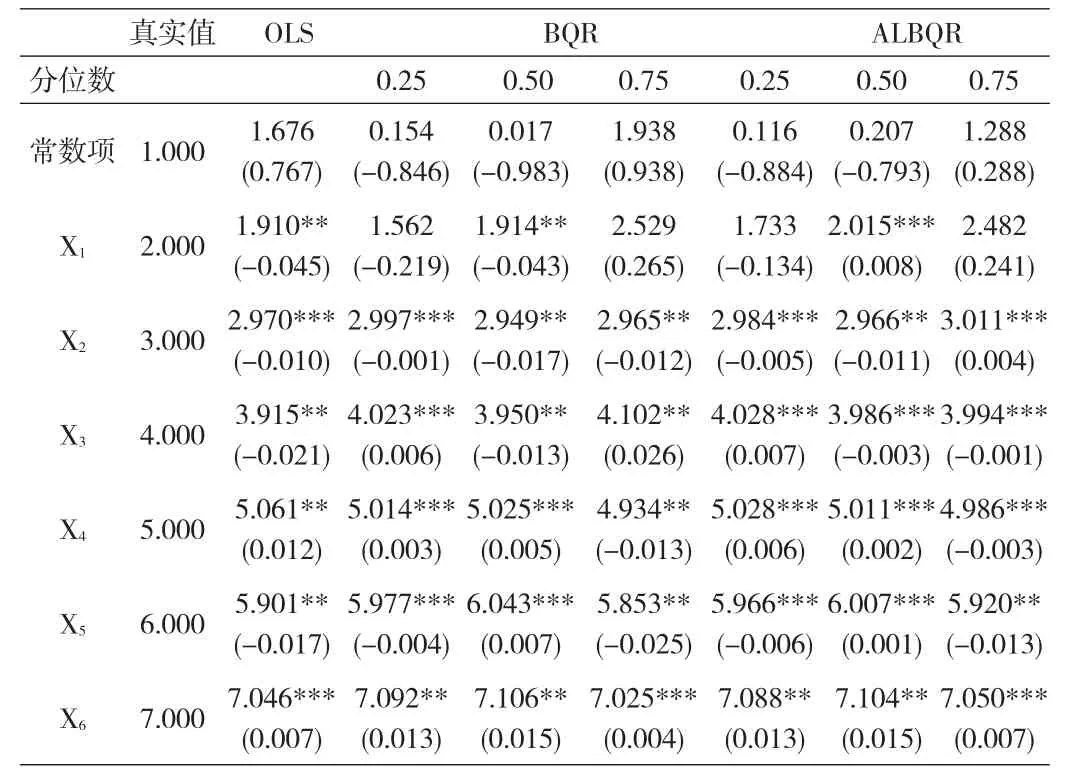
表3 仿真模拟结果(样本量N=100)
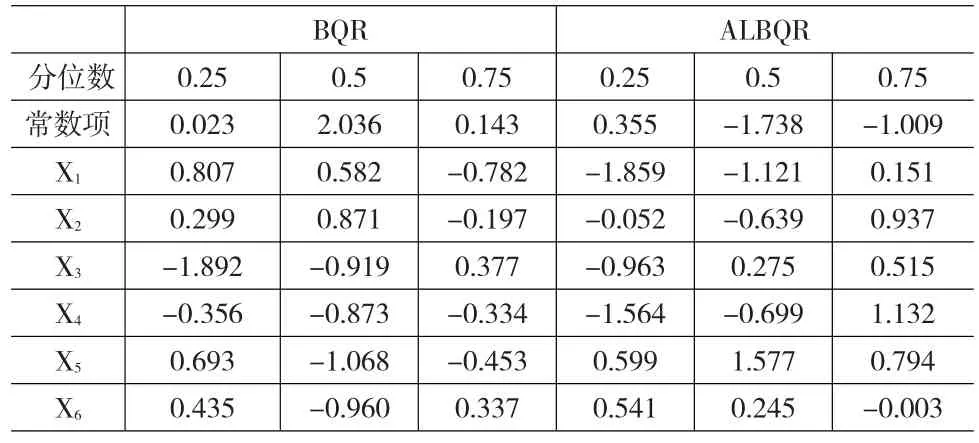
表4 MCMC链条收敛性判断(样本量N=100)
在表4,样本量为100时,BQR模型和ALBQR模型所有链条的Z统计量绝对值都小于2,均通过Geweke收敛性检验,因此判断这些MCMC链条收敛稳定,从而侧面印证前文关于ALBQR模型的分析结论是合理有根据的。
3 结束语
虽然贝叶斯分位数回归模型可以解决数据普的尖峰厚尾、结构突变等问题,也充分利用先验信息,但该方法没有很好地处理多维变量模型的维数灾难问题,本文在贝叶斯分位数回归方法基础上,采用自适应Lasso惩罚进行变量选择,构建了基于MH抽样算法的自适应Lasso惩罚贝叶斯分位数回归模型。仿真模拟实验表明,在小样本时,ALBQR模型的拟合性能更优也更稳健。
[1]陈耀辉,郭俊峰,殷文超.人民币升值对中小板市场波动的影响——基于贝叶斯分位数回归的分析[J].系统工程,2015,(1).
[2]Tibshirani R.Regression Shrinkage and Selection via the Lasso[J]. Journalof the Royal Statistical Society(Series B),1996,58(1).
[3]Zou H.The Adaptive Lasso and Its Oracle Properties[J].Journal of the American Statistical Association,2006,101(476).
[4]Koenker R,BassettG.Regression Quantiles[J].Econometrica:Jour⁃nalof the Econometric Society,1978,46(1).
[5]Tsionas E G.Bayesian Quantile Inference[J].Journal of Statistical Computation and Simulation,2003,79(3).
[6]Andrews D F,Mallows C L.Scale Mixtures of Normal Distributions [J].Journalof the Royal StatisticalSociety(Series B),1974,36(1).
(责任编辑/易永生)
0212
A
1002-6487(2016)19-0020-03
国家自然科学基金面上项目(71373219);国家自然科学基金青年项目(71103150);中央高校基本科研业务费专项资金资助项目(2013221012)
郭俊峰(1988—),男,江西赣州人,博士研究生,研究方向:金融计量经济学。

