二值型响应与连续型响应联合建模的变量选择
胡亚南,张陶陶,田茂再
(1.中国人民大学统计学院;2.中国人民大学统计研究中心,北京100875)
二值型响应与连续型响应联合建模的变量选择
胡亚南,张陶陶,田茂再
(1.中国人民大学统计学院;2.中国人民大学统计研究中心,北京100875)
由于多重响应变量之间可能存在相关性,文章考虑对二值型响应变量和连续型响应变量进行联合建模。利用probit模型,对二值响应引入了具有正态分布的潜变量,从而对多重响应建立线性回归模型,能得到二值变量和连续变量的联合分布。然后考虑回归系数会存在稀疏性,通过对似然函数加惩罚,从而对二重响应的回归系数和协方差矩阵的逆矩阵进行估计,达到参数估计和变量选择的目标。文中目标函数基于l1惩罚。数值模拟和实证分析展示了所提出方法的良好性质。
EM算法;多元正态分布;Probit模型;联合建模;LASSO;变量选择
0 引言
在一个具体问题中,人们所关心的响应变量可能是在不同尺度下测量,既有二值响应变量,也有连续型响应变量。要看协变量对响应变量的影响,此时如果对二值变量和连续变量分别进行建模,会忽略不同的响应变量之间的相关性,从而丢失有用的信息。基于这种考虑,对二值响应变量和连续型响应变量进行联合建模,从而有效利用样本观测信息,并更好的刻画响应变量之间的相关性。
有很多关于二值变量和连续变量的联合建模的方法被提出来。这些方法往往引入潜变量,对二值响应变量使用了probit模型,它引入服从正态分布的潜变量进行建模。Catalano&Ryan(1992)利用潜变量概念推导出了连续变量和离散变量的联合分布,并把模型应用到聚类数据。他们把二重响应变量的联合分布写成连续变量的随机效应模型与离散变量的probit模型乘积的形式。采用广义估计方程(GEE)的方法来估计参数。Albert&Chib(1993)根据数据增广的思想,利用精确贝叶斯的方法对类别响应变量进行建模分析。把二值响应的probit回归模型看作连续型潜变量的正态回归。由于潜变量能从合适的截断正态分布中产生,一旦潜变量的实现值已知,那么参数的后验分布可以从标准的线性模型结果中得出。数据增广的方法为分析二值回归模型提供了一般的结构。作者把probit模型应用到无序的多项响应变量和有序的多项响应变量,用贝叶斯的方法进行估计推断。Dunson(2000)提出了一个灵活的方法来对混合变量进行贝叶斯分析。通过利用广义线性模型来描述潜变量的联合分布,模型能适用于更广泛的数据结构。在文章所提出的结构下,新的模型可以推广到联合的二值变量、分类变量和连续变量。连续型响应变量和类别响应变量联合建模的一个难点在于缺乏自然的多元分布。Gueorguieva&Agresti(2001)提出了相关的probit模型来对聚类的二值型响应和连续型响应进行联合建模,他们对二值响应引入了服从正态分布的潜变量,并对这样一个相关的probit模型进行研究。作者对引入的潜变量和连续变量同时建立线性混合效应模型,采用MCEM算法估计参数。Liu etal.(2009)对纵向的二值和连续过程进行联合建模,并应用到戒烟试验中,这两个过程的相依性由无限制的回归系数所刻画;作者采用贝叶斯变量选择来估计参数,寻找稀疏模型。Holstetal.(2015)处理这类联合建模的问题,引入了潜变量和线性潜变量模型,提出了极大似然的估计方法,并且能分析含左删失、右删失的观测数据。
对二值型响应和连续型响应的联合建模,同时作回归分析,然而回归中的变量选择是统计研究的热点问题。选择稀疏模型,不但能提高预测的精确性,而且更好解释。随着大数据时代来临,高维数据越来越普遍,诸如最优子集等传统的变量选择方法在面临这些数据时,由于计算量太大,往往无法满足需求。基于惩罚函数的变量选择方法越来越受到统计学者的关注。这类方法是在最小二乘或极大似然目标函数上加上或者减去惩罚函数而得到新的目标函数,然后最优化目标函数,进而得到参数的估计。这种方法的优点在于参数估计和变量选择同时进行,大大提高了计算速度。
Tibshirani(1996)提出了lasso的方法,通过对回归系数作l1范数的惩罚,压缩系数,把一些绝对值较小的系数压缩为0,从而达到估计参数和变量系数的目的。lasso方法克服了传统变量选择方法的不足,在统计领域受到了极大关注。继而,lasso开始应用到其他模型中,并且也有很多文献对lasso进行改进。Tibshirani(1997)把lasso方法应用到生存分析领域,对Cox比例风险模型做变量选择。Zou(2006)对lasso方法做了改进,提出了自适应lasso,即对不同的回归系数施加不同的权重的惩罚,所得到的估计量具有良好的性质,并且这种方法具有0 racle性质。这些研究都是把lasso应用到单一响应变量的情形。Turlach (2005)把lasso扩展到多重响应变量的情形,通过对回归系数加惩罚,选择共同的解释变量。对于多重响应的变量选择问题,Simon etal.(2013)提出了区块降速算法来求解加group惩罚的目标函数,得到了回归系数的系数估计,但是没有考虑响应变量之间的相依性。Friedman etal.(2008)以多元正态分布为研究对象,用图lasso的方法得到协方差矩阵的逆矩阵的估计,简化了概率图模型的结构。Rothman etal.(2010)研究了多重响应的回归分析,既构建回归系数矩阵的稀疏估计量,同时又考虑了响应变量之间的相关性,通过最优化加惩罚的似然函数,得到回归系数和协方差结构的估计。
在实证分析部分,本文主要研究了国内生产总值(连续型响应变量)和是否为发达国家(二值响应变量)的联合建模。国内生产总值和是否为发达国家,作为衡量国家经济发展和评价综合国力的重要指标,都是经济研究中的重要课题,但在以往的研究中,多以其一为响应变量,考虑其影响因素进行建模。冶涛(2012)以固定资产投资总额、财政收入等六个解释变量建立GDP的多元回归模型,肖尧等(2009)研究汇率变动对经济增长的影响在发达国家与发展中国家的对比分析。两者分别的研究已经较为成熟,但本文考虑到国内生产总值和国家发达水平之间的相关性,对两者进行联合建模;然后,对二值响应引入服从正态分布的潜变量,然后对连续性变量和潜变量的联合分布进行建模。为了得到回归系数的稀疏估计,同时利用响应变量之间的相依性信息,我们对目标函数加自适应lasso的惩罚。由于二值型响应变量和连续型响应变量之间会存在响应性,我们考虑联合建模;然后,对二值响应引入服从正态分布的潜变量,然后对连续性变量和潜变量的联合分布进行建模。为了得到回归系数的稀疏估计,同时利用响应变量之间的相依性信息,我们对目标函数加自适应lasso的惩罚。
1 模型
1.1潜变量和probit模型
在二重响应变量的联合建模中,二值型响应变量的存在很大程度上增加了建模的难度,此时潜变量提供了一个实用且直观的方法来对离散型响应变量进行建模。本文二值型响应变量的probit模型引入了潜变量,即模型事先假定一个不可观测的连续型随机变量存在,并且潜变量超过一定的门限值时,假设一个二值事件发生。在对多重响应建模之前,我们首先回顾一下单变量的情形。考虑到线性模型

其中Y1i表示响应变量,是协变量,其中β0表示截距项。ϵi是误差项,且ϵi~N(0,σ2)。

当观测数据Zi是二值响应变量,与潜变量Y1i满足关系:由线性模型(1)误差项的假设,可以得出Zi满足probit模型
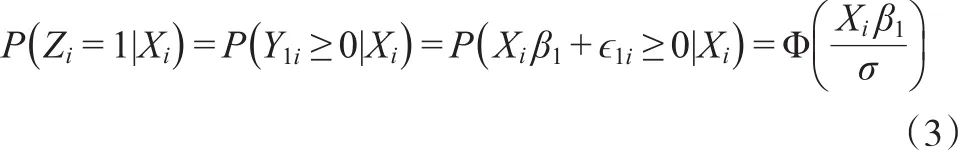
Φ(⋅)是正态分布的累积分布函数。一则,潜变量在具体应用中的体现;二则从统计角度来看,潜变量具有非常吸引人的地方,因为这样的假设下,二值响应的正态模型,有一个非常方便的形式。
1.2二重响应变量的联合模型
假设有n个观测,第i个观测的响应变量为(Zi,Y2i),其中Zi是二值型变量,我们引入潜变量Y1i,则Zi与Y1i满足方程(2);Y1i是连续变量。对二值型变量和连续型变量联合建模,那么相关的probit模型如下:

如果ρ=0,则Σ退化为对角矩阵。对二值响应Zi,引入了潜变量了Y1i来建模,即使用了probit模型.记Yi=(Y1i,Y2i),对方程(4),可改写为

其中B=(β1,β2),是系数矩阵。
1.3变量选择
统计学习中,有两个基本的目标,一则预测的精确性;二则找到相关的协变量,从而方便解释.当真实的模型有稀疏表示时,变量选择尤为重要。从式(4)中可以看出,当引入潜在变量之后,连续型响应和二值型响应的联合建模问题,转变为多重响应的线性回归模型,令X是n×p的设计矩阵,Y的n×2的响应变量矩阵,由于误差ϵ1,…,ϵn是独立同分布于N2(0,Σ),那么在给定X的情况下,多重响应的协方差阵为Σ。

由于不同的响应之间存在相关性,所以E所对应的协方差阵不是对角矩阵。为了方便起见,记Ω=Σ-1,那么模型(5)的对数似然表示:
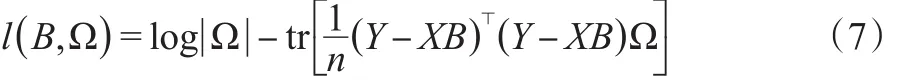
由于要对多重回归模型作变量选择,则考虑如下对系数惩罚的似然函数
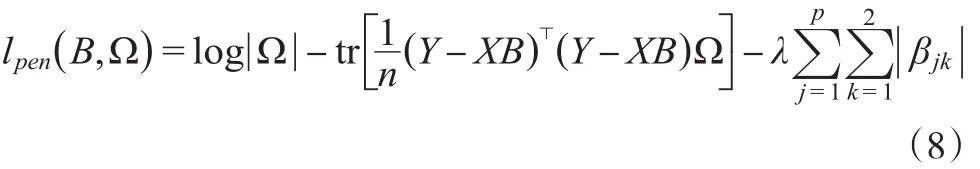
其中βjk是系数矩阵B中的元素,λ是调节参数。通过最优化目标函数从而得到参数的估计
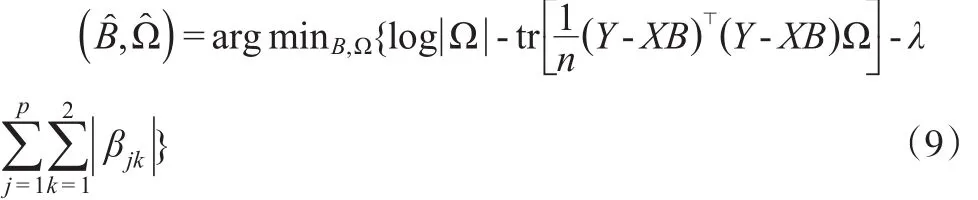
2 算法
由于对二值响应引入了潜变量,而潜变量是不可观测的。Dempster etal.(1977)提出了EM(expectation-maximization)算法。对于解决含缺失数据、潜变量等不完整数据,EM算法是一种行之有效的方法.Gueorguieva&Agresti (2001)在处理聚类的二值响应和连续型响应联合建模问题时,利用改进的EM算法得到相关probit模型的极大似然估计。本文也采用EM算法,用潜变量的条件期望代替潜变量。
2.1似然函数和条件分布
利用数据增广技术,引入潜变量Y1i,根据方程(2)和(4),得到完全数据(Y1i,Y2i,Zi)的概率密度函数

在已知联合分布(10)情形下,公式(11)可由简单的数值积分求解。
2.2计算步骤
要得到参数的估计,需要对目标函数(8)最大化。Rothman etal.(2010)给出了优化过程中的计算细节,这里只给出大致的计算步骤:
(2)E-步:由于Y1i是潜变量,无法观测到,但是其分布是知道的,因此利用它的条件分布,用期望值代替。基于当前的参数估计值根据条件分布用条件期望来代替潜变量Y1i;
考虑到EM算法是寻找的局部最优解,迭代过程需要设定模型参数的初始值其初始值的选取,利用分别建模的方法。
2.3选择调节参数
3 模特卡罗模拟
3.1模型设定
本文并未考虑对系数矩阵B的选择,只是简单设置满足稀疏性。令
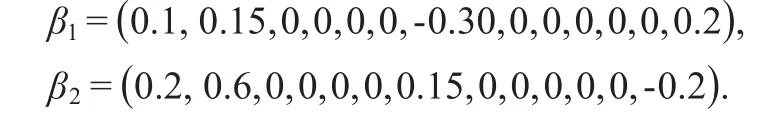
生成n×p的协变量矩X,每个行的观测Xi独立同分布于Np(0,ΣX),其中所有协变量的边际方差为1。误差矩阵的行向量ϵi来自于正态分布其中
根据方程(4),可以得到响应(Y1i,Y2i)的取值,由于Y1i是潜变量,根据方程(2),当Y1i≥0时,Zi=1;当Y1i<0时,Zi=0。则(Zi,Y2i)是要进行分析的观测。
3.2估计量
首先,采用数据增广技术,对二值响应Zi引入潜变量Y1i,然后用用条件期望E(Y1i|Y2i,Zi)来代替潜变量Y1i。在此基础上,为了比较所提出方法的表现,我们设置了对照模型。模拟中所展示的模型有:
模型1:对二值响应和连续型响应分别建模,不考虑变量选择;
模型2:对二值响应和连续型响应同时建模,不考虑协方差结构;
模型3:对二值响应和连续型变量同时建模,考虑协方差结构。
3.3评价标准
我们从参数的均方误差和稀疏指标选择两个角度来评估模型的好坏。
定义参数的均方误差为:
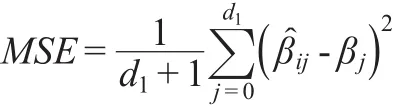
βj表示连续型响应变量或者二值响应变量所对应的回归系数向量,表示第i次重复所得到的参数估计向量,d1+1表示参数的维数。MSE就小,说明模型的估计效果越好。
度量稀疏性的指标包括敏感性(Sensitivity)和特异性(Specificity):
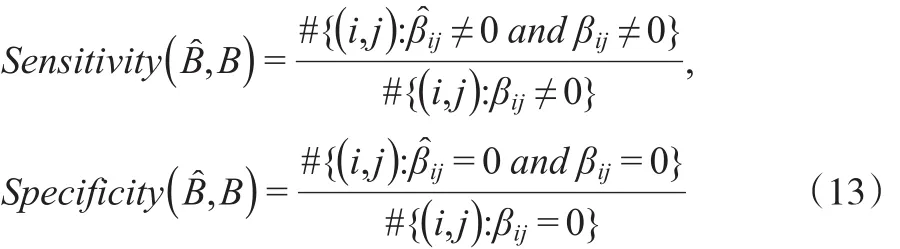
其中#表示计数。敏感性和特异性在0到1之间,越接近1,说明变量选择的效果越好。
3.4结果分析
(1)模型1利用一般线性模型拟合,并没有作变量选择,其结果展示敏感性全为0,特异性全为1,没有把有效的变量筛选出来,这在预期之中。
(2)在其他设置不变的情况下,随着样本量的增加,模型1-模型3的MSE变小;整体看来,模型2和模型3的特异性和敏感性变大,即变量选择的效果越好。
(3)在设置相同的情况下,连续型响应部分和二值响应部分,模型3的MSE较小,敏感性和特异性较大,这也反映了本文所提方法的优越性及合理性。一种我们所提出的方法在所有准则下表现最好。这表明,对所有组联合建模有助于提高预测精确性和估计。
(4)整体上看,连续型响应部分和二值响应部分比较,二值响应部分的敏感性和特异性较小,即变量选择效果较差。
(5)在其他设置不变的情况下,随着ρe的增加,模型3的敏感性和特异性增加。
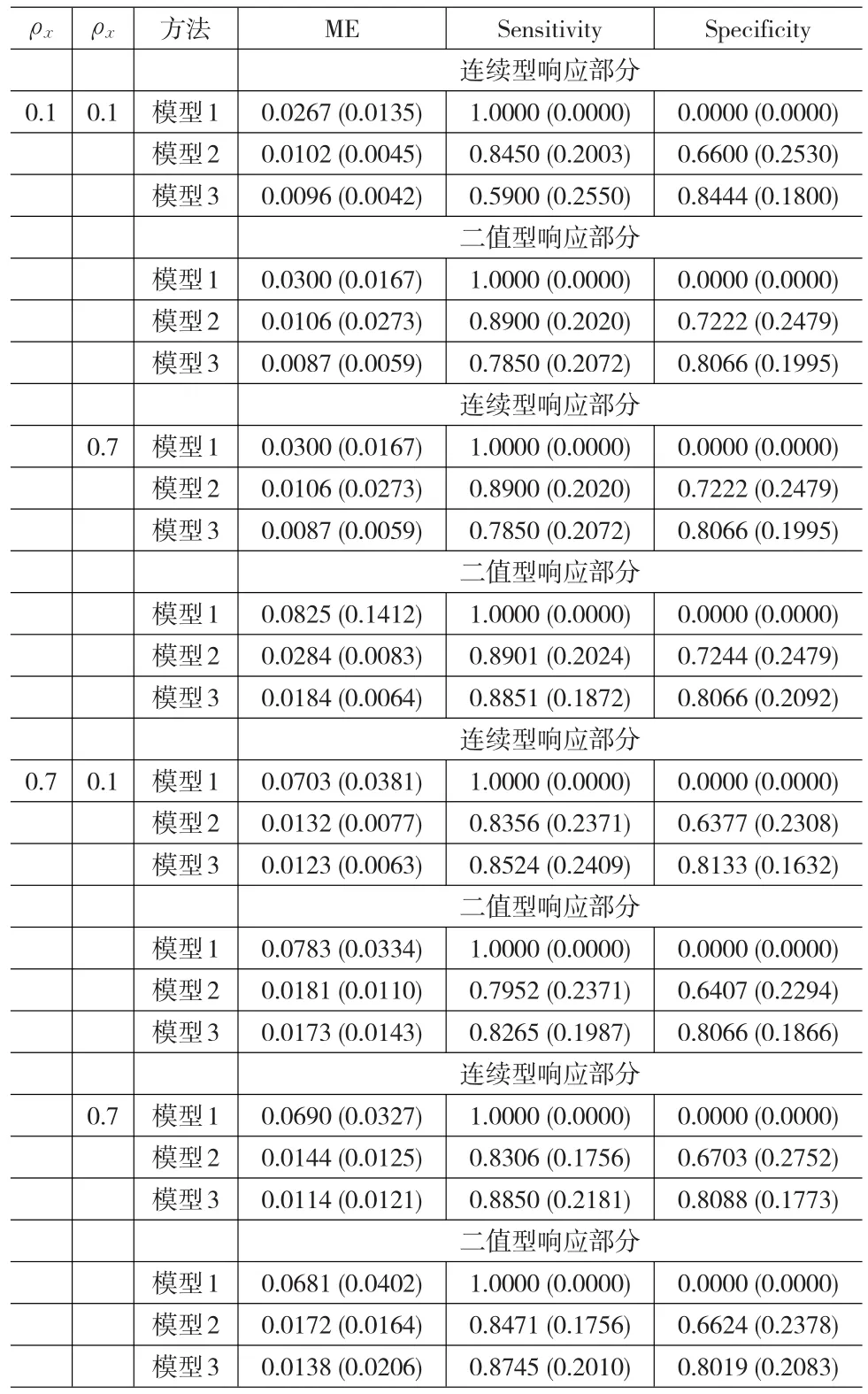
表1 当样本量为50时的模拟结果
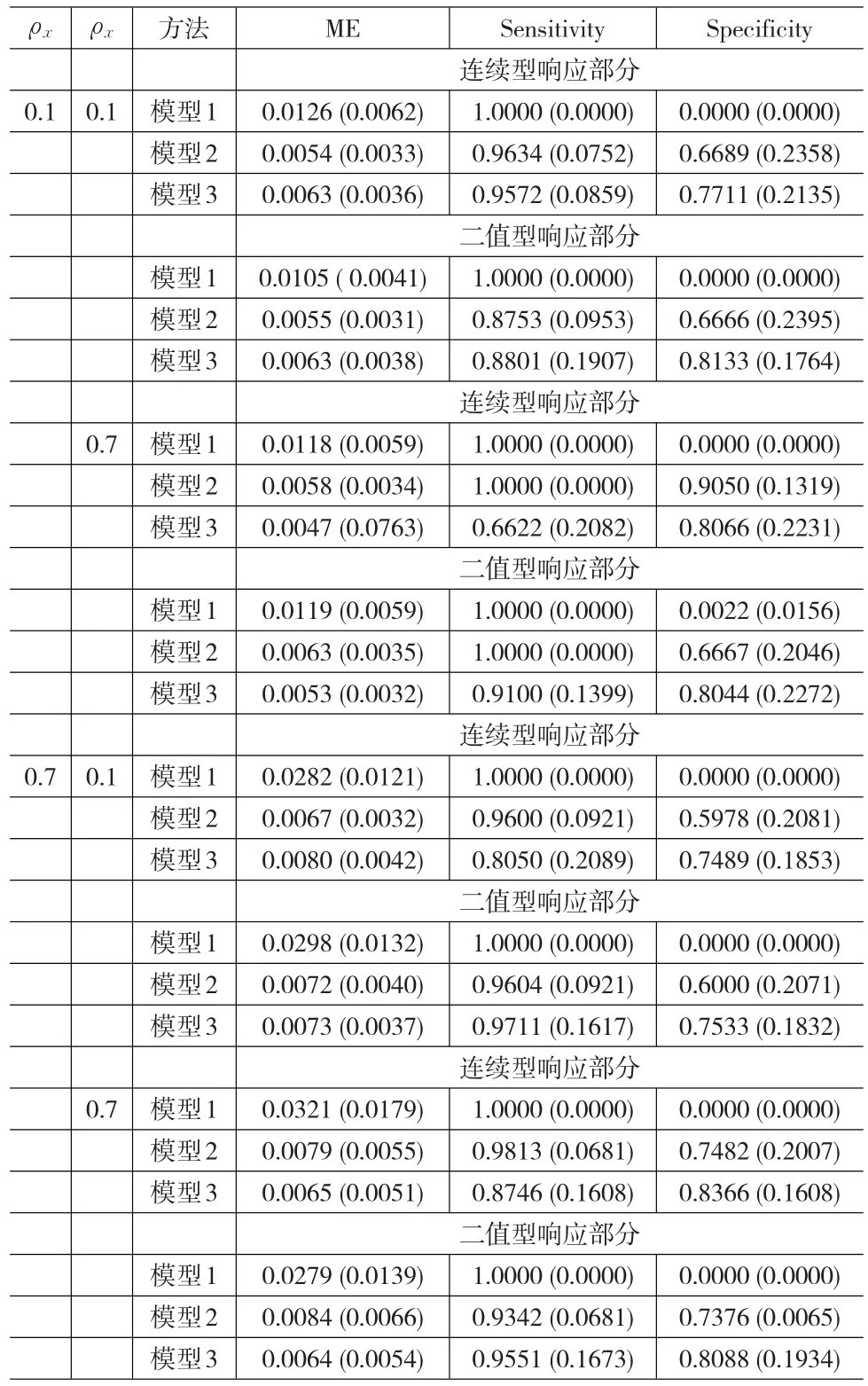
表2 当样本量为100时的模拟结果
4 实证
本文实证分析部分主要研究了国内生产总值和国家发达程度的联合建模。本文的数据来源为《国际统计年鉴》,除响应变量为国内生产总值和发达程度以外,还考虑的协变量包括:对外直接投资、外商直接投资、货物进口总额、货物出口总额、资本形成率、居民消费率、发电量七个经济类指标,以及森林资源、淡水资源、国土面积、二氧化碳排放量四个环境资源类指标。对所有变量信息汇总如表3。
运用本文方法对于二重响应变量进行联合建模,得到参数估计结果如表4。可以看出,6个协变量对发达程度有显著的影响,包括:对外直接投资、森林资源、国土面积、二氧化碳排放量、货物进口总额、货物出口总额;3个协变量对国内生产总值有显著的影响,包括:对外直接投资、发电量和货物进口总额。

表3 变量额汇总统计
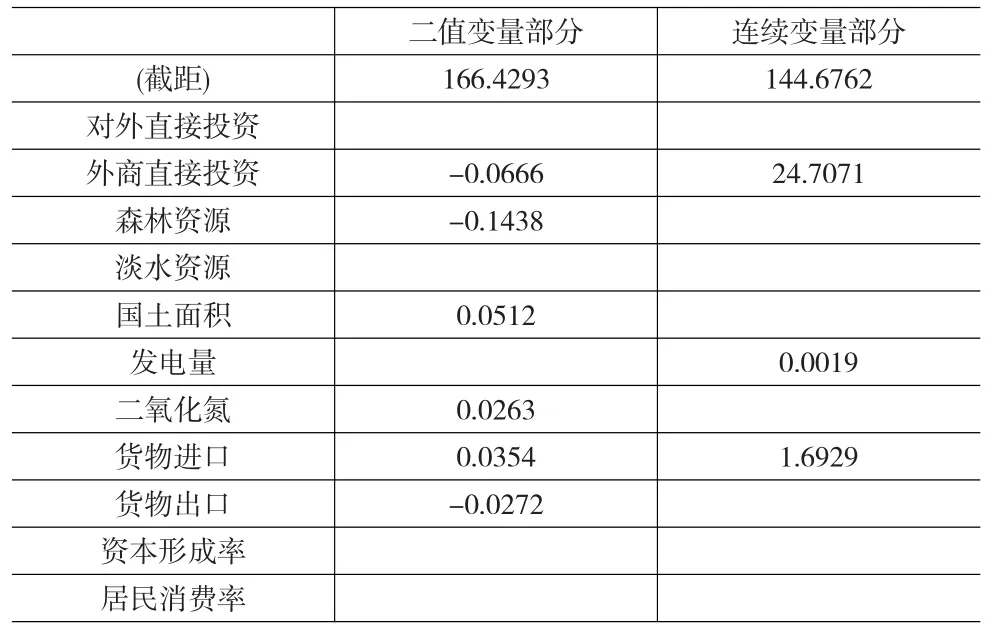
表4 系数估计
5 结论
多元回归是解决实际问题的一个常用工具。许多多元回归技术是为单个响应的情况设计的。对于多重响应变量的情况,一个通常的方法是应用单个响应变量的回归技术,分别对每个响应变量作回归分析。尽管这样很简单、也很流行,但是这样处理,会忽略不同的响应变量之间的联合信息。
在很多实际问题中,会观测到连续变量、二值变量等不同类型的数据,本文构造了多元线性回归来刻画连续型响应变量和二值响应变量的联合建模,并重点研究了变量选择问题。对二值响应引入了服从正态分布的潜变量,从而把问题转化为多重响应的多元线性回归的变量选择。本文在构造目标函数时,考虑了不同的响应变量之间的协方差,选取了l1惩罚,通过交叉验证的方法来选择调节参数。在模拟研究中,考虑不同的样本量以及不同结构的设计阵和协方差矩阵,并与其他方法比较,本文提出的方法利用不同的响应变量之间的信息,提高预测的精确性。表现出了一定的优势。
[1]Albert JH,Chib S.Bayesian Analysis of Binary and Polychotomous Response Data[J].Journal of the American Statistical Association, 1993,88(422).
[2]Catalano P J,Ryan L M.Bivariate Latent Variable Models for Clus⁃tered Discrete and Continuous Outcomes[J].Journal of the American Statistical Association,1992,87(419).
[3]Dunson D B.Bayesian Latent Variable Models for Clustered Mixed Outcomes[J].Journalof the Royal Statistical Society.Series B,Statis⁃ticalMethodology,2000.
[4]Friedman J,Hastie T,Tibshirani R.Sparse Inverse Covariance Esti⁃mationWith the Graphical Lasso[J].Biostatistics,2008,9(3).
[5]Gueorguieva R V,AgrestiA.A Correlated ProbitModel for JointMod⁃eling of Clustered Binary and Continuous Responses[J].Journal of the American StatisticalAssociation,2001,96(455).
[6]Holst K K,Budtz-Jorgensen E,Knudsen GM.A IatentVariableMod⁃elWith Mixed Binary and Continuous Response Variables[J].Staist⁃ics,2015.
[7]Liu X,DanielsM J,Marcus B.JointModels for the Association of Lon⁃gitudinal Binary and Continuous Processes With Application to a Smoking Cessation Trial[J].Journal of the American Statistical Asso⁃ciation,2012.
[8]Rothman A J,Levina E,Zhu J.Sparse Multivariate Regression With Covariance Estimation[J].Journal of Computational and Graphical Statistics,2010,19(4).
[9]Simon N,Friedman J,Hastie T.A Blockwise Descent Algorithm for Group-penalized Multiresponse and Multinomial Regression[J].Sta⁃tistics,2013.
[10]Tibshirani R.Regression Shrinkage and Selection via the Lasso[J]. Journalof the Royal Statistical Society.Series B(Methodological).
[11]Tibshirani R.The Lasso Method for Variable Selection in the Cox Model[J].Statistics in Medicine,1997,16(4).
[12]Turlach B A,VenablesW N,Wright S J.Simultaneous Variable Se⁃lection[J].Technometrics,2005,47(3).
[13]Zou H.The Adaptive Lasso and Its Oracle Properties[J].Journal of the American StatisticalAssociation,2006,101(476).
[14]肖尧,张达.汇率变动对经济增长的影响——基于发达国家与发展中国家的对比分析[J].金融教学与研究,2009,(06).
[15]冶涛.国内生产总值影响因素实证分析——以新疆GDP增长因素为例[J].金融经济,2012,(16).
(责任编辑/易永生)
021
A
1002-6487(2016)19-0004-05
国家自然科学基金资助项目(11271368);国家社会科学基金重点项目(13AZD064);教育部哲学社会科学研究重大课题攻关项目(15JZD015);北京市社会科学基金重大项目(15ZDA17);教育部高等学校博士学科点专项科研基金(20130004110007);教育部人文社会科学重点研究基地重大项目(15JJD910001);中国人民大学科学研究基金资助项目(15XNL008)

