基于多孔介质模型的网格畸变屏特性研究

王正鹤，赵辉，王菁

（郑州航空工业管理学院航空工程学院，河南郑州45004）

基于多孔介质模型的网格畸变屏特性研究

王正鹤，赵辉，王菁

（郑州航空工业管理学院航空工程学院，河南郑州45004）

以圆形管道内垂直于来流的圆形和环形网格畸变屏为研究对象，通过基于多孔介质模型的Reynolds-averaged Navier-Stokes方程对其产生的流场进行计算分析，得到了圆形管道内网格畸变屏特性的规律性结果，并通过了风洞实验的验证。计算和实验的结果均表明，在圆形管道内，相同面积比的圆形和环形网格畸变屏对流场的作用规律基本相同；具有相同压力损失系数的网格畸变屏的面积比越大，其后亏损区和非亏损区的速度越高；相同面积比的网格畸变屏的压力损失系数越大，其后亏损区与非亏损区域的速度差越大。

网格畸变屏；多孔介质模型；数值模拟；实验验证

1.引言

在工业生产或内流研究中，常需产生特定的非均匀速度分布。圆形管道是内部流动系统中的重要组件，如热交换器管道等。为在内流系统中进一步发挥圆形管道的作用，往往会使用满足特定要求的非均匀速度分布流场。这就要求对非均匀速度分布流场的产生机理和流场特性进行深入研究。而采用网格畸变屏是产生所需非均匀速度分布流场的一种简便且有效的方法[1-2]。

早期，主要凭借实验和经验的方法来获取生产及研究中所需的速度分布。1949年，Taylor和Batchelor[3]最先针对平面网格畸变屏对流体的作用进行研究，发现流体流过网格畸变屏后湍流度逐渐减小并提出了表征网格畸变屏对流场作用的一个关键参数——压力损失系数K。随后，学者们通过理论研究建立模型的方法研究网格畸变屏对流体的作用。Koo和James[4]对平行管道内的网格畸变屏的特性进行研究，建立了满足平行管道内网格畸变屏流动特征的非线性激盘模型。此模型首先把平行流管内均匀来流流过网格畸变屏的流动区域分为两个区域，用均匀的源项分布来代替均匀的网格畸变屏对均匀来流的畸变作用，建立气流流过网格畸变屏的连续方程和动量方程，求解得到流场分布的解析解。当网格畸变屏的压力损失系数在10以内时，模型计算得到的平行流管内流体流过网格畸变屏的流动特征与实际流动特征一致，因此，此模型在一定范围内可以较准确地预估平行管道内气流流过网格畸变屏所产生的速度分布。

近年来，随着计算流体动力学技术（CFD）和试验技术的发展，对流场内多孔性物体的研究得到了飞速发展。流场内多孔性物体的数值分析一般有2类方法：一类是对多孔性物体的精细结构进行微观数值模拟分析的方法；另一类是基于多孔介质模型的CFD方法。张生等[5]重点研究了网格畸变屏的金属丝间的相互影响，将网格畸变屏简化为二维平面管道内的圆柱群，对网丝具体结构进行CFD数值模拟分析。陈强等[6]将微型管道抽象成多孔介质模型，研究了微型管道的流动和传热特性。

为了预估圆形管道内均匀来流流过网格畸变屏后的速度分布，本文将通过基于多孔介质模型的RANS方程进行数值分析，获得圆形管道内网格畸变屏特性的规律性结果，并通过实验对此修正结果在预估圆形管道内均匀来流流过圆形和环形网格变屏后速度分布进行可靠性验证。

2．网格畸变屏的特性

从结构特性上来说，屏是一种多孔性物体（porous body）。图1给出了工业和内流研究所用的网格畸变屏的网格单元的结构。

图1 网格畸变屏网格单元示意图

网格畸变屏的孔隙率是表征屏的几何布局特征的一个重要参数。网格畸变屏的孔隙率定义为屏的流通面积与屏的总面积之比，其计算式[7]如式（1）所示

式中：α为金属网的孔隙率，l为相邻平行金属丝轴心间距，d为金属丝的直径。

从物理特性上来说，网格畸变屏对流体的流动主要有两个方面的作用：一方面是压力损失；另一方面是使流动方向发生偏转，即流线向屏的法线方向偏转。对于本文研究的垂直于来流放置的网格畸变屏，气流流过网格畸变屏后流场中流线偏转角度很小，可以忽略不计，因此主要考虑网格畸变屏对流体的压力损失作用。

压力损失通常用压力损失系数表示，压力损失系数是表征屏对流场作用的一个关键参数。无量纲压力损失系数K的定义[8]为式（2）。

式（3）为表征网格畸变屏的压力损失系数与孔隙率间关系的经验表达式[9]。

式中：K为金属网的压力损失系数，△P为气流流经金属网前后的压差，Un为金属网前来流的法向速度，Red为基于网丝直径的来流雷诺数。

3．多孔介质模型

管道内网格畸变屏计算区域包括上游流域、网格畸变屏处的多孔介质域和下游流域。上游流域和下游流域是不可压缩的有旋流动，流动控制方程表达如下

式中：xi为流动方向，ui是xi方向的流速，P为液体的压力，μ为动力粘度系数。

相对于非多孔介质的流动，多孔介质内的流动要受到附加的阻力作用，包括粘性阻力和内部阻力，因此会产生额外的压力损失。依据考虑了粘性阻力和内部阻力的Darcy多孔介质模型[10]，可以确定通过多孔介质的牛顿流体的速度和压降

式中：ai是粘性阻力系数，bi是内部阻力系数。

式（6）表示牛顿流体工质通过多孔介质时压力梯度项和阻力项相平衡，反映了通过多孔介质的流动特性与流体工质以及流动条件间的相关性。数值求解RANS方程来分析网格畸变屏的畸变特性需要将式（6）作为动量源项添加在式（5）中进行求解。

4．计算模型及数值方法

采用ICEM软件的多块结构化网格技术对计算域进行网格生成。利用多孔介质模型，将网格畸变屏设置为多孔介质域，采用数值求解三维RANS方程的方法，对网格畸变屏对来流的畸变作用分别进行分析研究，数值研究方法的计算域结构如图2所示，其中面积比λ为网格畸变屏的面积与计算域流道横截面积的比值，u1为均匀进气速度，将网格畸变屏下游分为亏损区和非亏损区两个区域，可认为亏损区和非亏损区的速度均匀分布，则非亏损区域的速度为u2，亏损区域的速度为u3。采用ICEM软件的多块结构化网格技术对计算域进行网格生成。通过网格无关性验证，为确保计算结果不受网格分布及网格数量的影响，计算域网格数取20万以上，并确保壁面网格的y+＜=3。

图2 数值模拟计算域

采用商用CFD软件CFX数值求解RANS控制方程，湍流模型选用标准k-ε模型。CFX软件中采用多孔介质域分析网格畸变屏内流动可根据式（1）确定其孔隙率系数。在CFX计算过程中，利用多孔介质理论的Darcy定律，根据式（2）和式（6），通过设定多孔介质域中源项的一次损失系数和二次损失系数以在动量方程中增加动量损失源项，从而较好地把网格畸变屏对压力场的影响表达出来。其余计算条件为：给定进口总温为288.15 K，总压为101325 Pa，气流角为轴向，出口给定流量值。

5.结果分析

5.1 数值分析结果

为了验证数值模拟方法的可靠性，本文首先对二维平行管道内面积比为30%、50%和70%的网格畸变屏对来流的作用分别进行数值模拟分析，并将数值模拟结果与已经试验结果验证的非线性激盘模型的结果进行对比，如图3所示。对平行管道内

网格畸变屏对来流作用进行数值分析的结果与非线性激盘模型理论结果的误差在2%以内。关于数值分析结果与非线性激盘模型所得的结果并不完全一样，这是由于非线性激盘模型基于非亏损区域内气流为无粘流的假设，而本文中研究的是粘性流动，此误差是可以接受的。因此，采用多孔介质模型进行数值模拟网格畸变屏对气流作用的数值方法是可靠的。

图3 数值结果和非线性激盘模型结果对比

对圆形管道内面积比分别为30%、50%和70%的圆形和环形网格畸变屏对流场的影响规律进行数值模拟分析，通过调整网格畸变屏的压力损失系数，分析不同的网格畸变屏对流场的作用，结果如图4所示，图中模拟值1和模拟值2分别表示圆形和环形网格畸变屏的数值模拟结果。

图4 圆形管道内网格畸变屏特性数值分析结果

对比激盘模型的理论结果和通过数值模拟分析，得到圆形管道内环形畸变网和环形畸变网对气流的作用结果，可以看出，对圆形管道内具有相同面积比的环形网格畸变屏和圆形网格畸变屏，其后气流速度分布随压力损失系数定量变化规律是基本相同的；具有相同压力损失系数的网格畸变屏的面积比越大，其后亏损区和非亏损区的速度皆越高；相同面积比的网格畸变屏的压力损失系数越大，其后亏损区与非亏损区域内速度差越大。数值计算分析圆形径向负荷分配屏的速度分布与压损系数的关系的结果与二维激盘模型分析的理论结果在趋势发展走向上是一致的，但定量数值存在较大的差异。相比于平行管道内网格畸变屏下游速度分布，对圆形管道内具有相同压力损失系数的网格畸变屏而言，其下游流场亏损区域内的速度比u3/u1较大，而非亏损区域内的速度比u2/u1较小。

4.2 实验验证结果

图5 低速风洞实验台

为了进一步确定数值分析圆形管道内网格畸变屏特性结果的可靠性和适用范围，在一台低速风洞中通过实验测量以进行验证。实验台结构如图5所示，气流进气通过由电机驱动的电扇进行抽吸，气流速度通过节流堵锥调节。网格畸变屏安装座上游2.2D处具有轴向均布的五个静压孔，以获取来流速度的大小。网格畸变屏下游的总压和静压分布通过皮托管来测量，皮托管安装在网格畸变屏下游1.5D处。

对于不同面积比的圆形和环形网格畸变屏，分别选取压力损失系数为2.17、5.06，面积比30%、50%和70%的网格畸变屏进行实验测量，对其中每种类型的网格畸变屏的测试实验均重复进行5次以排除随机误差。

实验测试选用的压损系数为2.17和5.06的两类网格畸变屏分别命名为屏1和屏2，其具体几何参数和物理参数在表1中列出。

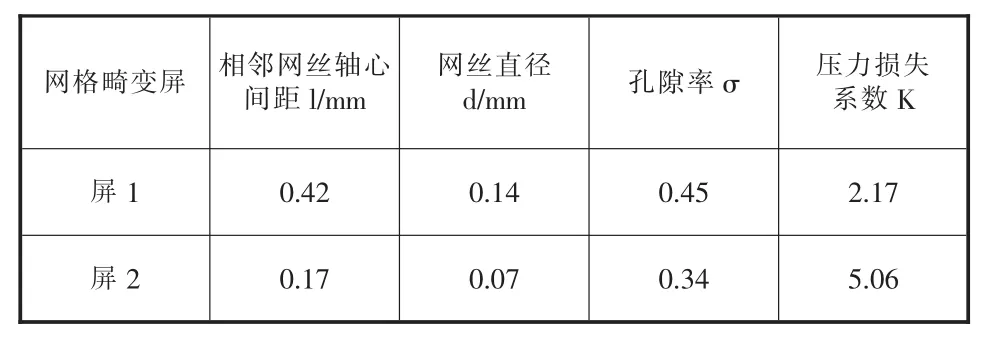
表1 网格畸变屏参数

实验测得网格畸变屏的压力损失系数与速度比的关系如图6所示，图中虚线为对圆形管道内网格畸变屏数值模拟结果进行最小二乘拟合所得到的参考曲线，实验值1和实验值2分别表示圆形和

环形网格畸变屏的实验测量结果。图6中可以看出，与通过多孔介质模型进行数值模拟的结果类似，圆形管道内，对具有相同面积比的环形网格畸变屏和圆形网格畸变屏，实验测得其后气流速度分布随压力损失系数定量变化规律基本相同。

图6 数值计算结果与实验结果对比

通过对比实验结果和数值修正结果，实验结果和数值修正结果误差在3.5%以内。数值模拟结果与实验测量值并不完全一样，这是由于实验中通过离散的测量点来获取网格畸变屏下游的非均匀流场分布，下游流场速度突变区域的径向尺寸较小，通过具有一定尺寸的皮托管测量无法完全精准。本文数值修正结果对圆形管道内气流流过网格畸变屏后的速度分布预估结果在网格畸变屏压力损失系数小于7的范围内具有可靠性。

6．结论

采用基于多孔介质模型的RANS方程求解技术，对圆形管道内网格畸变屏对气流的畸变作用进行分析研究，分别计算了3种面积比和15种压力损失系数的圆形管道内网格畸变屏的畸变特性，获得了规律性结果，并通过实验验证修正结果的可靠性。研究结果表明，数值分析结果在网格畸变屏的压力损失系数小于7时能够准确预估网格畸变屏的畸变特性，预估其后速度分布规律。

[1]Wakeland R S,Keolian R M.Measurements of resistance of individual square-mesh screens to oscillating flow at low and intermediate Reynolds numbers[J].Journal of fluids engineering,2003,125(5):851-862.

[2]施网兴，张戎，刘西鹏，等.发动机进口畸变模拟网机理研究[J].推进技术，1994，04：14-21.

[3]Taylor G I,Batchelor G K,Dryden H L,et al.The effect of wire gauze on small disturbances in a uniform stream[J]. The Quarterly Journal of Mechanics and Applied Mathematics,1949,2(1):1-29.

[4]Koo J K,James D F.Fluid flow around and through a screen[J].Journal of Fluid Mechanics,1973,60(03):513-538.

[5]张生，任文成，屠宝锋，等.畸变网CFD数值模拟研究[J].沈阳航空航天大学学报，2013，05：27-32.

[6]陈强，杨静宇，董涛，等.微管道换热器多孔介质模型分析及应用[J].机械工程学报，2004，04：108-113.

[7]Ko odziej A,ojewska J.Experimental and modelling study on flow resistance of wire gauzes[J].Chemical Engineering and Processing:Process Intensification,2009,48(3): 816-822.

[8]Annand W J D.The resistance to air flow of wire gauzes [J].Roy Aero Soc,1953,57:141–146.

[9]Dunn W,Tavoularis S.The Use of curved screens for generating uniform shear at low Reynolds numbers[J].Experiments in fluids,2007,42(2):281-290.

[10]Chew J W,Lapworth B L,Millener P J.Mathematical modeling of brush seal[J].Int J Heat Fluid Flow,1995,16 (6):494-500.

编辑：冯惟榘

Study on the Characteristics of Gauze Screens Based on Porous Medium Model

WANG Zhenghe，ZHAO Hui，WANG Qing
（School of Aeronautical Engineering,Zhengzhou University of Aeronautics,Zhengzhou Henan 45004）

An empirical approach is presented for the analysis of axisymmetric flow through plane wire gauze screens perpendicular to the flow partially filling the cross-section of a circular straight duct by using the Reynolds-averaged Navier-Stokes solution based on the porous medium model.Experiments with these axisymmetric partial blockage screens were found to be in fair agreement with the predictions of the approach.The results show that in a circular pipe,the dimensionless velocity ratios of flow through circular and annular wire gauze screens of same pressure loss coefficient are nearly equivalent.Moreover,with a fixed pressure loss coefficient,the ratio of the area of the screen in a circular pipe is lager,the dimensionless velocity ratio inside the wake region is larger,while that outside the wake region is smaller. The velocity difference between the wake region and the nonwake region increases nonlinearly with the increase of the pressure loss coefficient of screens.

gauze screens；porous medium model；numerical simulation；experimental verification

TB4

A

2095-7327（2016）-11-0030-05

王正鹤（1988-），女，河南洛阳人，郑州航空工业管理学院航空工程学院助教，硕士研究生，主要研究领域为叶轮机械气动力学、压气机非定常流动；赵辉（1976-），男，河南省孟津市人，教授，博士研究生，主要研究领域为并联机器人、智能优化、五轴数控技术；王菁（1991-），女，河南省南阳市人，硕士研究生，主要研究领域为机载电子设备、卫星导航系统。

河南省教育厅科学技术研究重点项目(15A590001)。