新型电容式MEMS加速度计数字接口电路设计
李宗伟,丛 宁,熊兴崟,韩可都,杨长春
(1.中国科学院地质与地球物理研究所,北京100029;2.中国科学院大学,北京 100049)
新型电容式MEMS加速度计数字接口电路设计
李宗伟1,2,丛 宁1,2,熊兴崟1,2,韩可都1,杨长春1
(1.中国科学院地质与地球物理研究所,北京100029;2.中国科学院大学,北京 100049)
MEMS加速度计接口电路主要采用传统sigma-delta架构实现,但这种方式中的电路失调电压很容易产生积分饱和现象.为解决这个问题,本文设计了一种可以用于钻井、石油勘探等微弱信号检测的新型数字电容接口电路.该设计在电容式MEMS加速度传感器基础上,采用FPGA实现数字三阶环路滤波器,构成5阶sigma-delta系统.采用数字环路滤波器降低了ASIC模拟电路版图设计与芯片测试难度,利于快速优化环路滤波器设计参数,改善系统稳定性和优化系统噪声性能.前置放大器采用一种相对简单的相关双采样技术,能够有效减小前置放大器的失调电压.根据MEMS加速度计前置放大器输出信号符合正态分布的特点,设计了带有一定预测功能的8-bit瞬时浮点ADC,实现模拟与数字环路滤波器互联.在200Hz带宽内,该接口电路系统噪声基底达到53.09ng/rt(Hz),满足系统噪声设计要求.前置放大器与ADC采用XFAB XH018混合信号CMOS工艺流片,开环测试表明,前置放大器的灵敏度和噪声分别为0.69V/pF和3.20μV/rt(Hz).
接口电路;MEMS;sigma-delta;ADC
1 引言
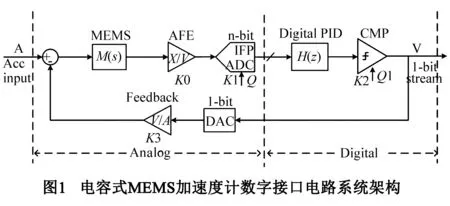
相对于传统加速度检波器,MEMS(Micro-Electro-Mechanical System)加速度计具有体积小、成本低、灵敏度高、容易集成等优势,同时闭环时具有动态范围大、线性度好与带宽高等优点,其应用范围越来越广泛,如汽车、智能手机、钻井勘探[1,2]等领域.在MEMS加速度计信号检测的方法中,电容检测是一种主要的检测手段,具有低噪声、低温度系数和高灵敏度等特点.电容检测加速度计需要专用的读出电路处理电容信号,目前主要是采用开关电容电路来检测MEMS电容变化信号[3~7].开关电容检测电路主要包括前置放大器、PID(Proportion-Integration-Differentiation)控制器以及静电力反馈等模块,静电力反馈实现闭环控制,可以达到良好的线性度以及大动态范围.电容检测加速度计系统主要采用sigma-delta架构[2,4~7],即传感器的电容信号经过前置放大器转换成电压信号,然后经过模拟PID环路滤波器调整并经过1bit比较器CMP(Comparator)输出比特流,最后经过1bit DAC(Digital-to-Analog-Converter)实现静电力闭环控制.受接口电路电子噪声影响,特别是前置放大器以及PID控制器噪声水平限制,上述sigma-delta接口电路架构目前的噪声水平在1μg/rt(Hz)左右,很难实现高灵敏度需求.在上述sigma-delta架构中PID控制器目前主要采用模拟办法实现,对ASIC(Application Specific Integrated Circuit)版图设计要求比较高,如参数匹配要求等.此外,在ASIC设计与实现过程中,由于器件工艺误差等因素,前置放大器和PID控制器等模块会产生失调电压,而失调电压会使得存在积分器的电路产生积分饱和.故实际中想要测试得到系统模块的具体参数比较困难,特别是测试PID参数,目前没有十分有效的测试手段.
为了解决失调电压而产生的积分饱和等问题,采用数字方式实现成为一种趋势.微弱信号数字处理方式在MEMS陀螺仪[8,9]中发展比较早,即电容信号转化为电压信号后采用ADC(Analog-to-Digital-Converter)将代表加速度信号的电压信号数字化后通过FPGA(Field-Programmable-Gate-Array)或者DSP(Digital-Signal-Processor)进行处理.这样可以降低ASIC版图对PID的设计要求,同时采用FPGA或者DSP可以快速优化PID的设计参数,提高产品研发效率.这种数字处理方案近几年才开始在MEMS加速计中应用[3,10~12],如Colibrys公司与Hewlett-Packard公司在MEMS加速度计sigma-delta架构中均开始使用ADC进行数字化处理.基于上述数字方案可以消除积分饱和与消除模拟PID的噪声对系统噪声影响等优点,本文对数字架构MEMS加速度计进行系统建模,理论分析了信号传递函数与量化噪声传递函数,引入ADC所产生的量化噪声对系统噪底的影响,根据系统噪声要求确定采用新型数字方案所需ADC的位数.文中分析了前置放大器AFE的工作原理,引入了一种相对简单的相关双采样技术用于消除前置放大器偏置电压.然后在非均匀量化ADC[3,13~15]的基础上,根据MEMS加速计输出信号的分布特点,引入新型瞬时浮点ADC,优化了ADC量化噪声对系统的影响.最后给出芯片前置放大器AFE开环测试时噪声测试结果以及线性测试结果.
2 系统架构
在MEMS加速度计sigma-delta闭环读出电路基础上,引入瞬时浮点ADC,使得前置放大器AFE(Analog-Front-End)输出的模拟信号直接转化为数字信号,然后将数字信号在FPGA/DSP中进行数字处理并通过1bit比较器输出bit流,最后通过1bit DAC进行静电力反馈实现闭环控制.本文的五阶系统是由MEMS传感器与三阶数字PID控制器构成,能有效增加系统的线性范围与提高系统噪声水平.系统引入ADC后其噪声性能会受到量化器量化噪声的影响,为确保系统噪声性能要求,需要确定系统所需ADC的位数,具体分析如下.
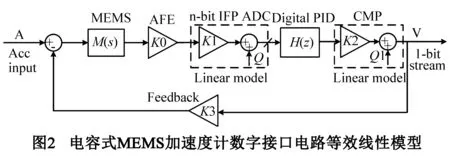
根据图2所示系统线性模型,可以根据系统的输入输出关系:
V=((A-K3V)M(s)K0+Q)H(z)K1K2+Q1
(1)
根据式(1)可以得到系统的信号传递函数STF以及量化噪声传递函数NTF表达式如下:
(2)
(3)
(4)
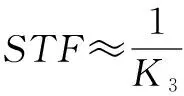
(5)
(6)
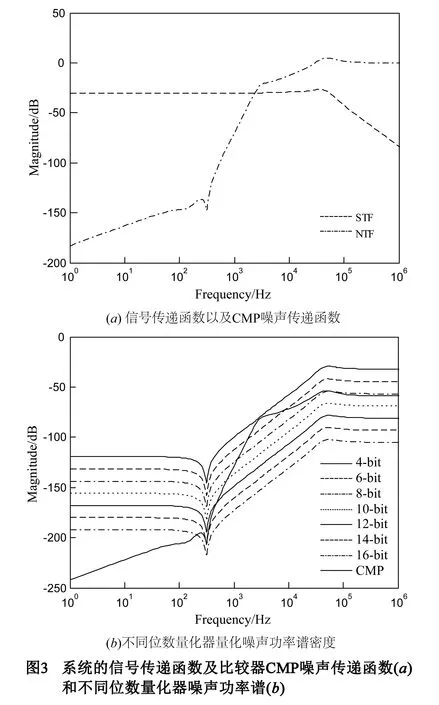
若Vfs=5V,仿真得到1-bit量化器CMP与n-bit量化器(n=4,6,8,10,12,14,16)的噪声功率谱密度如下图3(b)所示,在200Hz带宽内,仿真得到ADC量化噪声Q对系统的影响远大于比较器量化噪声Q1对系统的影响.本文实现系统的输入范围为±0.4g,动态范围大于120dB,为了达到高灵敏度需求,系统的噪声基底要低于-130dBg/rt(Hz).故在系统设计时需要考虑ADC的量化噪声对系统噪声的影响,ADC的位数至少8-bit.
3 前置放大器
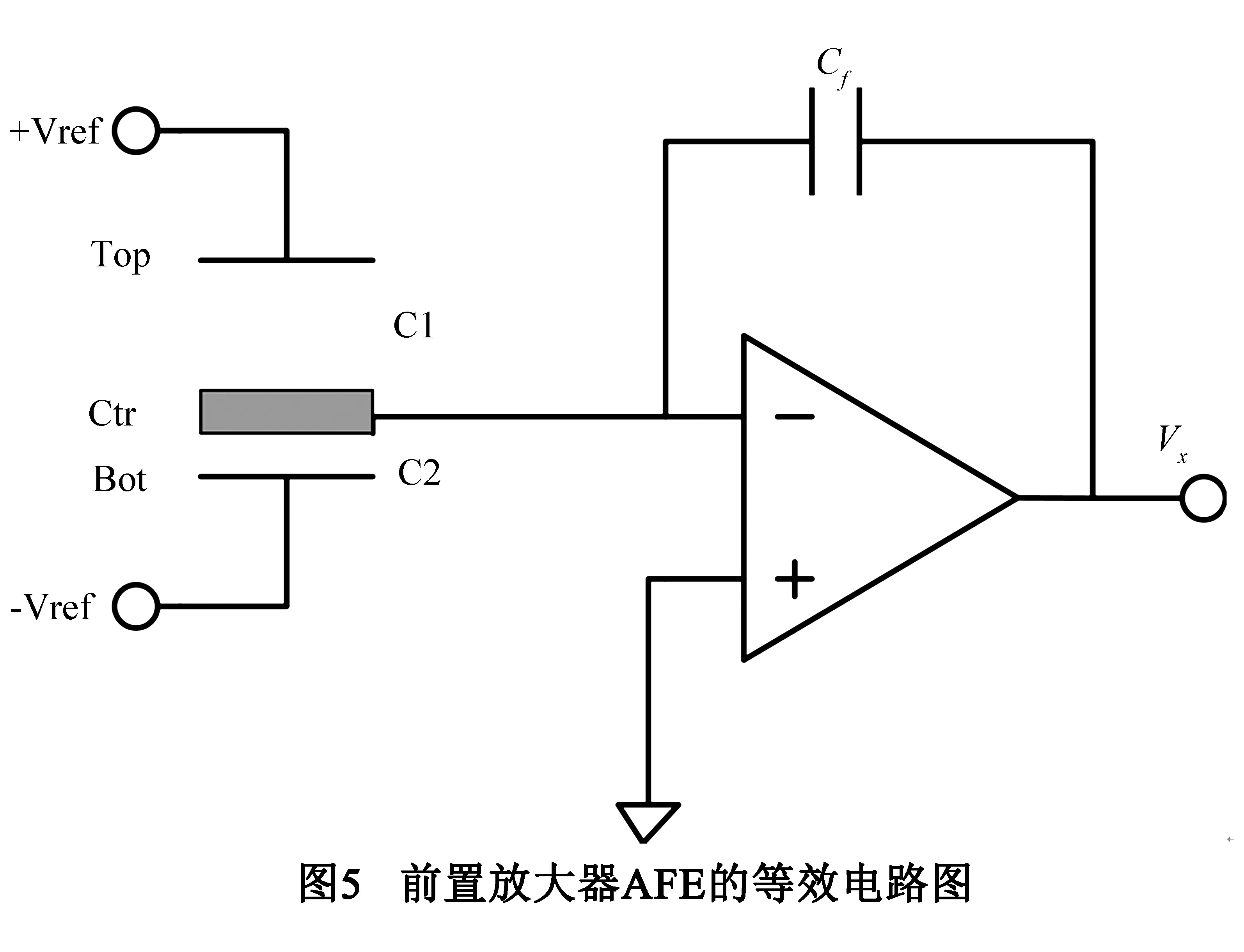
前置放大器是为了完成将电容式MEMS加速度计传感器电容变化量转化为电压的核心部分,其电路偏置电压对后面调理电路PID影响很大,一般采用相关双采样技术[6,16,17](Correlated Double Sampling,CDS)进行消除.与文献[6,16,17]所采用的CDS技术相比,本文所设计相关双采样技术结构简单,易于实现并能够有效降低电路偏置电压,同时降低了对时钟的需求,其实现原理图如下图4所示.其中VP/VN是加在MEMS传感器电极上的正负参考电压,VCOM是共模电压,其大小为(VP+VN)/2,VT/VC/VB是三明治MEMS加速度计的三个电极.在检测阶段开始前,开关phsg接通VC使得中间极板上的电压为VCOM,进行清零,这样可以保证phsi接通后放大器输入端电压基本一致.检测开始后,ph2阶段读出电容变化量并转化为电压信号输出给后续电路.当传感器受到外界加速度信号影响的情况下,质量块产生位移变化,位移变化会产生电容变化,而电容变化量通过AFE转化为电压量输出,完成读出过程.检测结束后ph1阶段对反馈电容进行清零并存储电路失调电压,并在下一个周期的ph2阶段进行抵消失调电压.最后系统输出的bitstream利用开关phtc与phbc进行数字反馈,实现闭环操作.前置放大器AFE的等效电路如图5所示,当质量块产生位移变化x时,对应的上下极板电容差为:
(7)
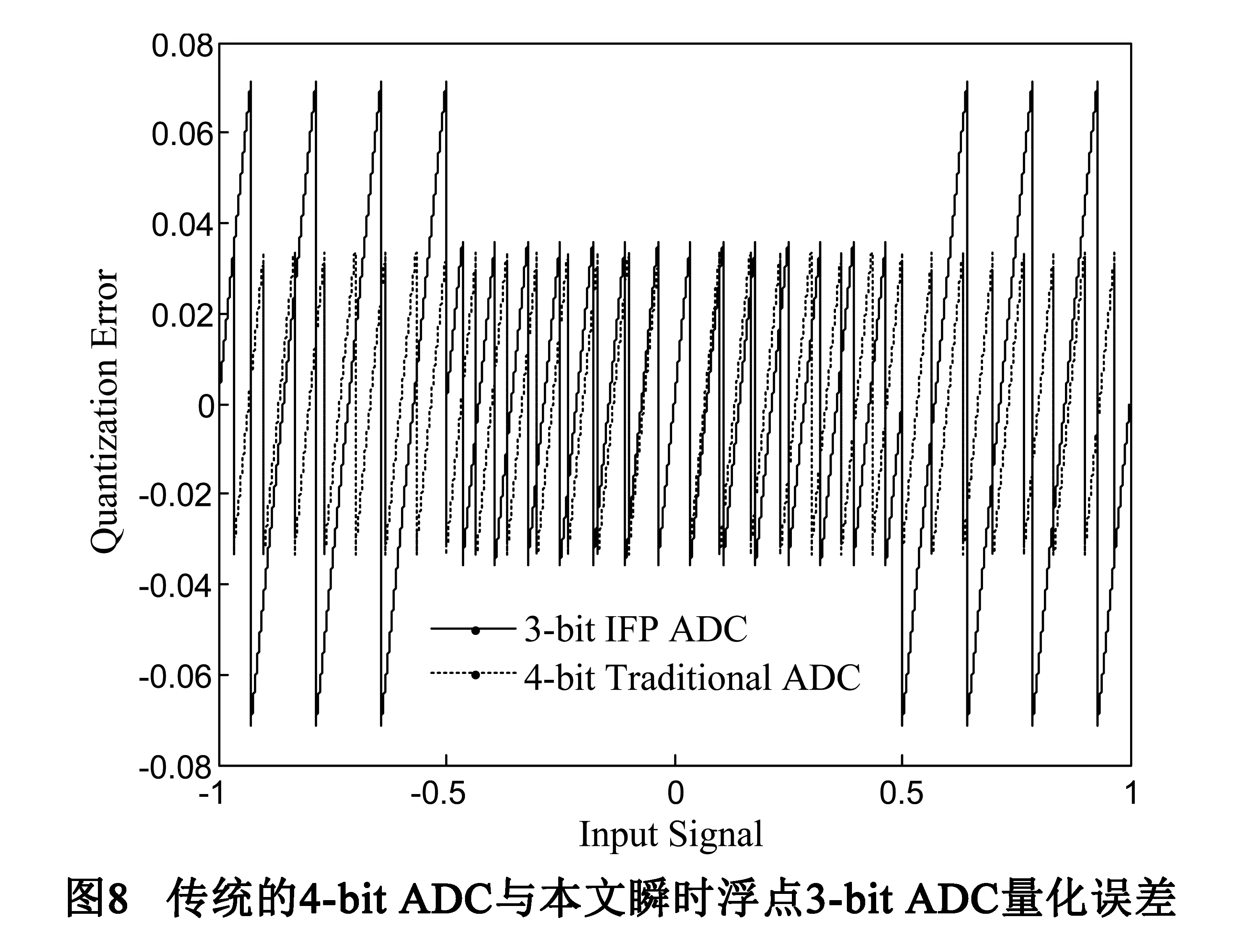
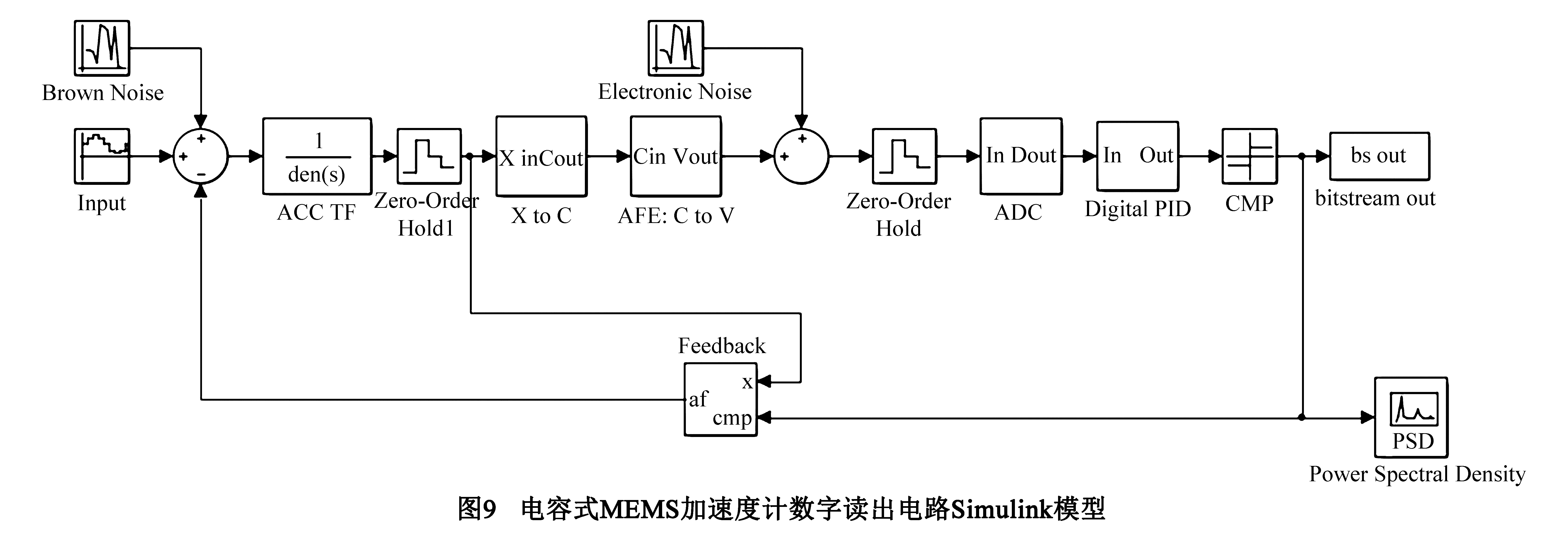
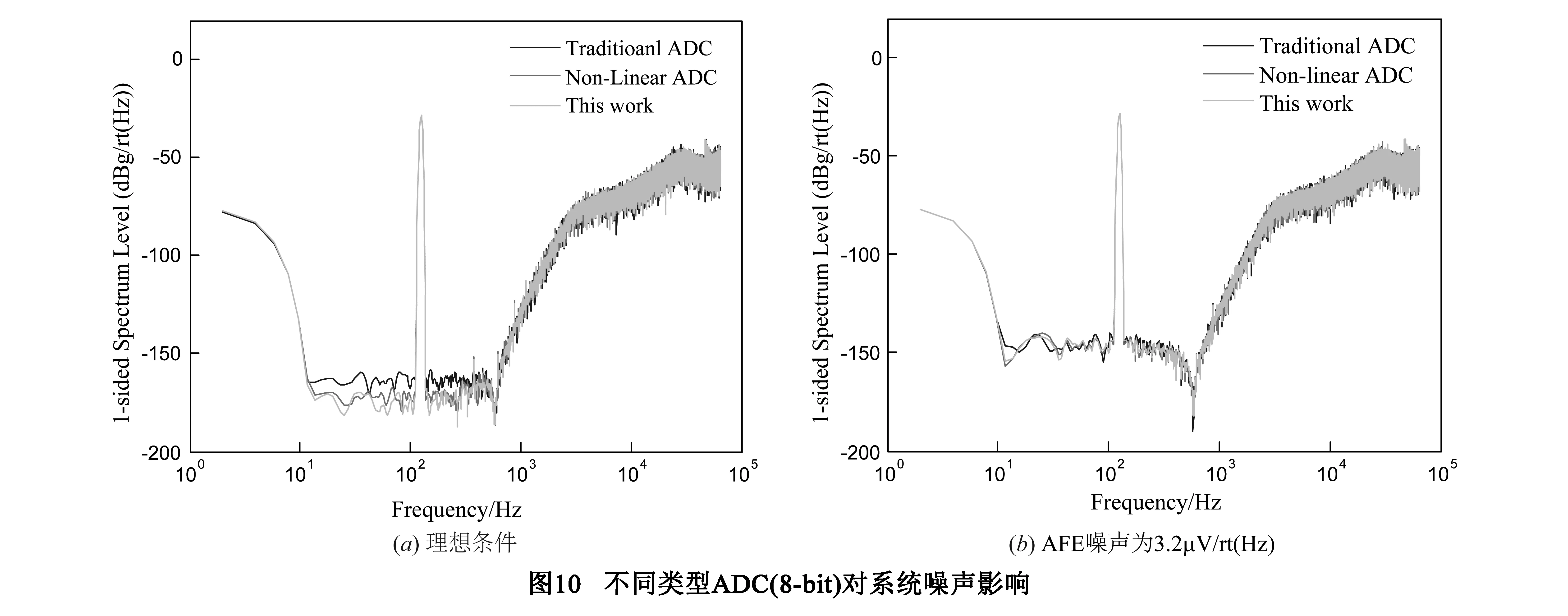
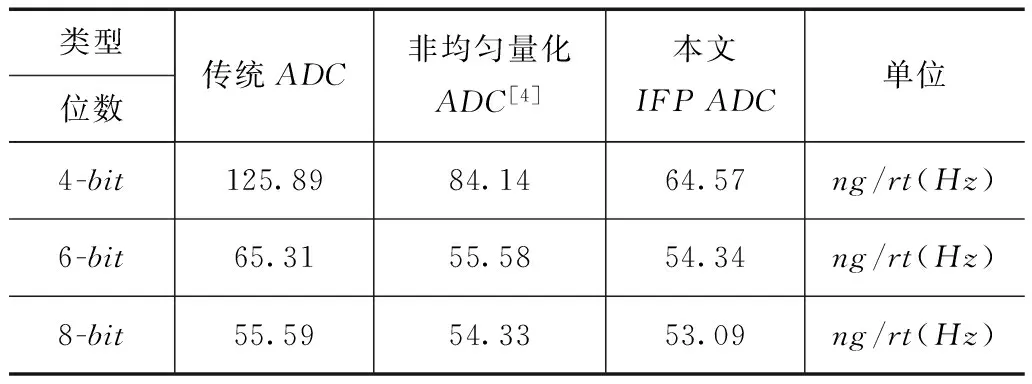
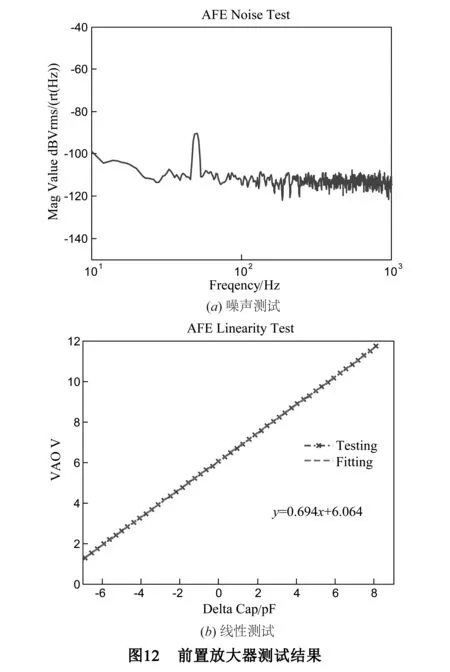
当x< (8) 前置放大器AFE输出的模拟信号Vx通过ADC转化为数字信号,然后交给数字环路滤波器PID进行处理.为实现量化处理,同时满足系统噪声要求,本设计采用了ADC为8-bit瞬时浮点SAR ADC.所谓瞬时浮点是指此n-bit ADC可以在一定程度上预测输入信号大小,并根据输入信号调整参考源电压大小,达到大信号量化误差大小信号量化误差小,实现(n+1)bits或者更高的分辨率,如下图6所示.当输入信号幅度大于Vref/2时,参考电压保持Vref不变,按照LSB1进行量化并输出对应的数字码;当输入信号幅度在Vref/2与Vref/4之间时,调整参考电压为Vref/2,按照LSB2进行量化输出对应的数字码;当输入信号的幅度小于Vref/4时,将参考电压改变为Vref/4,根据LSB3进行量化并输出数字信号.采用瞬时浮点ADC的主要是因为MEMS加速度计读出信号的分布在在ADC输入范围内不是均匀分布的,从仿真与实际测试结果看,该加速度计系统的信号符合正态分布,如下图7所示.与文献[4,13~15]所提到的非均匀量化ADC相比,本设计的主要优点是既符合MEMS加速度计信号呈现正态分布需求,也能够适应信号分布不具备任何特点的需求,实际应用更加广泛.考虑到ADC转换速率以及实际设计的复杂度,本文设计了8-bit瞬时浮点SAR ADC,在信号中心范围内达到了10-bit分辨率.图8比较了4-bit传统型ADC与本文所提到的瞬时浮点3-bit ADC的量化误差,在中心值附近,本文方法所设计的3-bit ADC的量化误差与4-bit传统ADC量化误差相同,采用本文提到的方法可以有效减小ADC面积.此外,适当的增加不同的参考电压,如Vref/8等,可以进一步提高ADC的性能. 本文基于三明治MEMS加速度计模型,搭建了五阶Simulink系统模型如下图9所示.在本设计中主要噪声包括布朗噪声、前置放大器噪声以及KT/C噪声[18~23].由于PID采用数字方式如FPGA实现,能够有效避免模拟方式实现PID产生的放大器噪声以及KT/C噪声等,故在系统建模时数字PID不会引入噪声.假定以上噪声均为高斯白噪声,参考实际前置放大器噪声测试结果,如图12(a),系统建模时取放大器噪声为3.2μV/rt(Hz),ADC的位数取8-bit,分别代入传统的ADC即均匀量化ADC、非均匀量化ADC[4,13~15]和本文IFP ADC,仿真噪声频谱图结果如下图10所示.图10(a)所示结果为表示ADC的位数相同时,系统引入文献[4,13~15]中的非均匀量化ADC的噪声水平优于引入传统均匀量化ADC的噪声水平,引入本文设计的瞬时浮点ADC时系统噪声水平优于引入非均匀量化ADC时的噪声水平.表1所示不同类型ADC和同一类型ADC不同位数时的仿真结果,无论哪种类型的ADC随着位数的提高,系统的噪声基底会明显改善.从表1所示结果可以得到,电容式MEMS加速度计使用本文设计IFP ADC作为量化器,且ADC的位数大于等于8-bit时,其量化噪声对系统噪声的影响可以忽略.从实验结果可以看出,当IFP ADC的位数大于等于8-bit时,新型电容MEMS加速度计数字接口电路的整体噪声性能主要受制于前置放大器的噪声性能.当IFP ADC的位数为8-bit时,在200Hz带宽范围内系统的噪声基底为53.09ng/rt(Hz).图10(b)表示受制于前置放大器布朗噪声、放大器噪声以及开关热噪声等的影响,ADC位数高于8-bit时对系统噪声的改善效果十分有限,这与前面理论分析时确定ADC的位数为8-bit相对应. 本设计的前置放大器与ADC采用XH018混合信号CMOS工艺进行流片,模拟电压为12V,数字电压为3.3V,版图如下图11所示.整个芯片的面积为8.44mm2,其中前置放大器与高压开关的面积为1.91mm2,ADC的面积为1.29mm2.采用安捷伦35670A对前置放大器进行噪声测试,测试结果如图12(a)所示,在200Hz带宽内,其输出噪声基底约为3.20μV/rt(Hz).结合芯片上电容补偿阵列测得AFE开环的灵敏度为0.69V/pF,如图12(b)所示,同时AFE可测的MEMS传感器电容变化范围大于±6pF. 表1 不同类型ADC以及不同位数对系统噪声性能 本文在传统的sigma-delta电容式MEMS加速计读出电路系统中引入了ADC,完成系统建模与仿真.通过仿真与理论分析了采用本文的数字方案所需ADC的位数与系统噪声的关系,为系统模型提供支撑.根据仿真结果确定达到系统对噪声的要求,需要ADC的位数至少为8-bit.本文采用的前置放大器采用了一种较简单的相关双采样实现方案,既消除电路失调电压,又降低了AFE电路对时钟的需求.根据AFE输出信号符合正态分布的特点,提出了IFP ADC,既适应与本文所设计的MEMS加速计系统,也适应于其他微弱信号检测电路系统,应用范围较非均匀量化ADC更加广泛,同时相同位数的IFP ADC所产生的量化噪声较均匀量化ADC和非均匀量化ADC产生的量化噪声对系统噪声的影响更小.此外,ADC量化后的数字信号交由数字PID处理,降低了模拟PID版图设计复杂度,能够有效提高PID参数优化效率,消除了模拟方案PID噪声对系统性能的影响,消除了电路失调电压产生的积分饱和现象.通过仿真,当IFP ADC为8-bit时,在200Hz带宽内,本文设计的 5阶MEMS加速度计系统的噪声可以达到53.09ng/rt(Hz),噪声优于设计需求.前置放大器和ADC采用XH018工艺进行流片,开环测试结果显示AFE的噪声为3.20μV/rt(Hz),开环增益为0.69V/pF,达到系统设计要求. [1]Wang Yucai,Chodavarapu Vamsy P.Design of a CMOS readout circuit for wide-temperature range capacitive MEMS sensors[A].15th Int’l Symposium on Quality Electronic Design[C].Santa,CA,USA,2014.738-742. [2]Laine J,Mougenot D.Benefits of MEMS based seismic accelerometers for oil exploration[A].Solid-State Sensors,Actuators and Microsystems Conference[C].Lyon,France,2007.1473-1477. [3]Pastre M,Kayal M,Schmid H,et al.A 300Hz 19b DR capacitive accelerometer based on a versatile front end in a 5th-order delta sigma loop[A].Proceedings of the 35th European Solid-State Circuits Conference (ESSCIRC’09) [C].Athens,Greece,2009.288-291. [4]Schmid H,Sigel S,Pastre M,et al.An internally non-linear ADC for a sigma delta accelerometer loop[A].International Symposium on Circuits and Systems Nano-Bio Circuit Fabrics and Systems[C].Paris,France,2010.2155-2158. [5]Saxena G D,Thamarai V.Modeling and Simulation of High Performance Sixth Order Sigma-Delta MEMS Accelerometer[A].International Conference on Computational Intelligence and Communication Systems [C].IEEE,2011.527-531. [6]Honglin Xu,Xiaowei Liu,Qiang Fu,et al.A high-order closed-loop ΣΔinterface for micro-machined accelerometer sensor[J].Analog Integrated Circuits and Signal Processing,2015,82(2):401-410. [7]Petkov Vladimir P,Boser Bernhard E.A fourth-order sigma delta interface for micromachined inertial sensors[J].IEEE Journal of Solid-State Circuits,2005,40(8):1602-1609. [8]Gaisser A,Geiger W,Link T,et al.New digital readout electronics for capacitive sensors by the example of micro-machined gyroscopes [J].Sensors and Actuators A,2002,97-98: 557-562. [9]Reinhard Neul,Udo-Martin Gmez,Kersten Kehr,et al.Micromachined angular rate sensors for automotive applications[J].IEEE Sensors Journal,2007,7(2): 302-309. [10]Fang Chen,Weizheng Yuan,Honglong Chang,et al.Low noise vacuum MEMS closed-loop accelerometer using sixth-order multi-feedback loops and local resonator sigma delta modulator[A].2014 IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS) [C].IEEE,2014.761-764. [11]Zwahlen P,Nguyen A M,Dong Y F,et al.Navigation grade MEMS accelerometer[A].23rd IEEE International Conference on Micro Electro Mechanical Systems[C].IEEE,2010.631-634. [12]Robert G Walmsley,Palo Alto.Three phase capacitance-based sensing[P].US: 8661901B2,2014-03-04. [13]Z Zhang,G C Temes.Multibit oversampled Σ-ΔA/D convertor with nonuniform quantization[J].Electronics Letters,1991,27(6): 528-529. [14]Bingxin Li,Tenbunen H.Sigma delta modulators using semi-uniform quantizers[A].Circuits and Systems,ISCAS[C].IEEE,2001.I456-I459. [15]Bingxin Li,Tenhunen H.A second order sigma delta modulator using semi-uniform quantizer with 81dB dynamic range at 32x OSR[A].Solid-State Circuits Conference(ESSCIRC)[C].Firenze,Italy,2002.579-582. [16]O’Donnell R.Circuit techniques for reducing the effects of op-amp imperfections: Autozeroing,correlated double sampling,and chopper stabilization[J].Proceedings of the IEEE,1996,84(11):1582-1583. [17]Payandehnia P,Maghami H,Meng Xin,et al.Sequential interstage correlated double sampling: A switched-capacitor technique for high accuracy systems[A].2014 IEEE 57th International Midwest Symposium on Circuits and Systems (MWSCAS) [C].IEEE,2014.262-265. [18]Yun Weijie.A surface micromachined accelerometer with integrated cmos detection circuitry[D].University of California,Berkeley,1992. [19]Biter Boga,Ilker Ender Ocak,Haluk Kulah,et al.Modeling of a capacitive Σ-ΔMEMS accelerometer system including the noise components and verification with test results[A].22nd International Conference on Micro Electro Mechanical Systems (MEMS) [C].2009.821-824. [20]Gabrielson T B.Mechanical-thermal noise in micromachined acoustic and vibration sensors[J].IEEE Transactions on Electron Devices,1993,40(5): 903-909. [21]Boser B E,Howe B T.Surface micromachined accelerometers[A].IEEE 1995 Custom Integrated Circuits Conference[C].IEEE,1995.337-344. [22]Haluk Kulah,Junseok Chae,Khalil Najafi.Noise analysis and characterization of a sigma-delta capacitive silicon microaccelerometer[A].12th International Conference on Solid-State Sensors,Actuators and Microsystems (Transducers03) [C].Boston,USA,2003.95-98. [23]Haluk Kulah,Junseok Chae,Khalil Najafi.Noise analysis and characterization of a sigma-delta capacitive microaccelerometer[J].IEEE Journal of Solid-State Circuits,2006,41(2):352-361. 李宗伟 男,1987年2月出生于山东聊城市.2010年毕业于青岛科技大学,之后进入中国科学院地质与地球物理研究所进行硕博连读,主要从事MEMS传感器系统设计、模数混合电路设计及MEMS接口电路ASIC设计方面的有关研究. E-mail: lizongwei@mail.iggcas.ac.cn 丛 宁 女,1987年12月出生,吉林松原人.2010年毕业于东北石油大学电子与信息技术专业,2010年进入中国科学院地质与地球物理研究所,现为硕博连读生,从事数模混合电路设计方面的有关研究. E-mail: congning@mail.iggcas.ac.cn A New Type Capacitive MEMS Accelerometer Digital Interface Circuit Design LI Zong-wei1,2,CONG Ning1,2,XIONG Xing-yin1,2,HAN Ke-du1,YANG Chang-chun1 (1.InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China;2.UniversityofChineseAcademyofSciences,Beijing100049,China) The circuit offset often causes integration saturation in the traditional sigma-delta interface of capacitive MEMS accelerometers.To address this problem,a new type of capacitive digital interface circuit used for downhole exploration and oil detection is designed.This paper presents a MEMS-based 5th-order sigma-delta capacitive accelerometer,where the 3rd-order digital loop filter is realized using FPGA.This will reduce the ASIC analog circuit layout design and chip testing difficulties and is easy to optimize the loop filter parameters,which can be used to improve the system stability and optimize the noise performance.The analog-frond-end amplifier (AFE) is realized by using a simple correlated double sampling (CDS),which is one effective method to reduce circuit offset of AFE.According to the Gaussian distribution of AFE output signal,one new type 8-bit instantaneous floating point ADC (IFP ADC) is designed.The IFP ADC is used to convert analog signal of AFE to digital signal to feed the 3rd-order digital loop filter.The whole system provides a significantly low noise floor 53.09ng/rt(Hz) overall a 200 Hz bandwidth.In this work,the AFE amplifier and ADC were successfully fabricated by using XFAB XH018 mixed-signal CMOS process.Furthermore,the sensitivity and noise floor of the AFE amplifier are 0.69V/pF and 3.20μV/rt(Hz) in open loop measurement,respectively. interface circuit;MEMS;sigma-delta;ADC 2015-08-19; 2016-02-18;责任编辑:李勇锋 国家重大科研装备研制(No.ZDYZ2012-1-06-04);国家科技重大专项(No.2011ZX05008-005) TN432;TP212 A 0372-2112 (2016)10-2507-07 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.10.032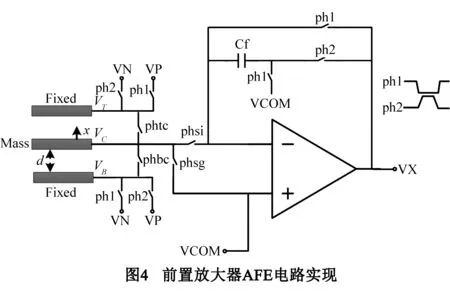
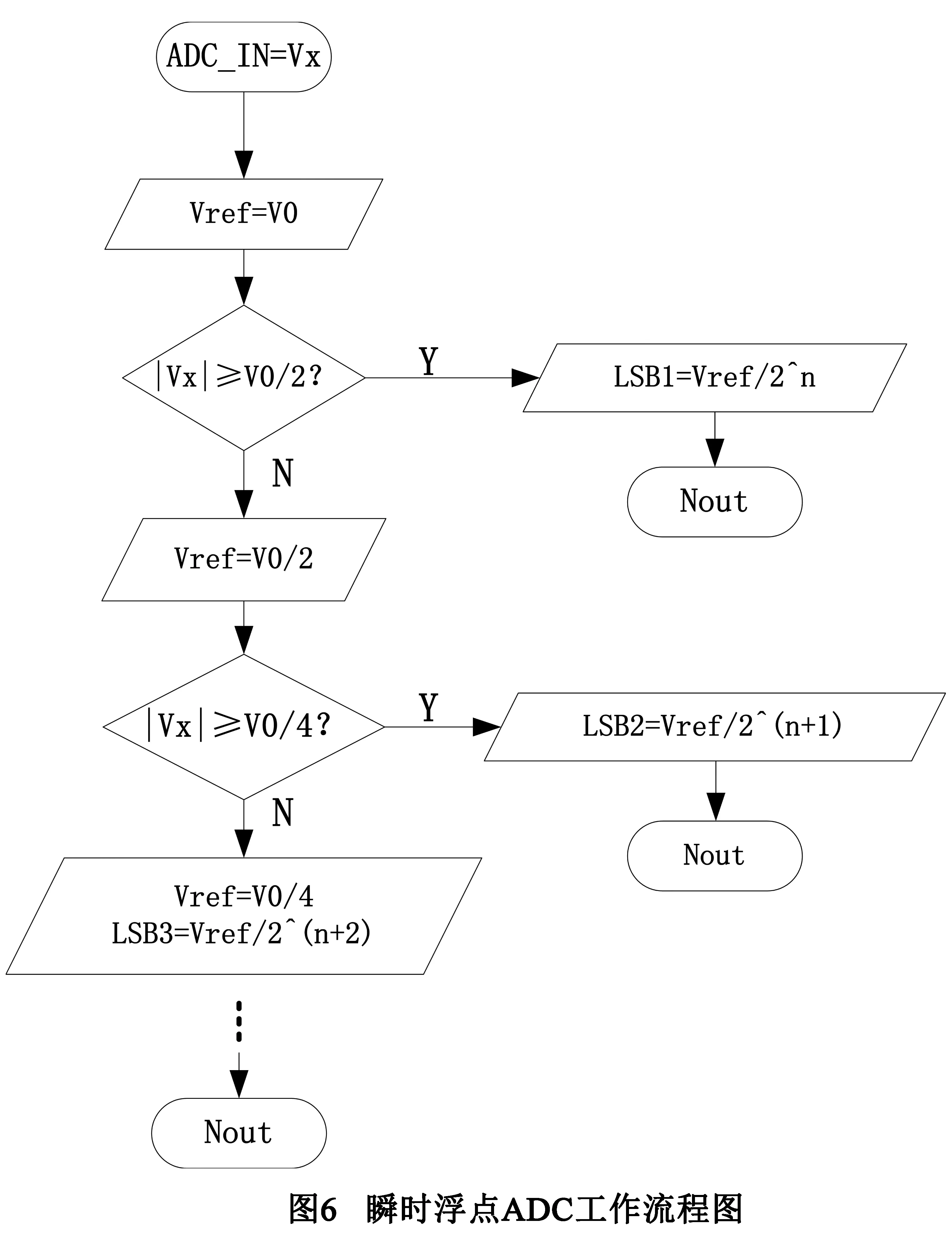
4 瞬时浮点ADC
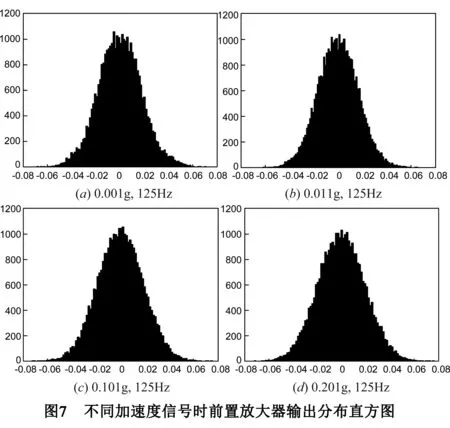
5 系统仿真与测试

6 结论



