基于重加权l1范数惩罚的远近场混合源定位算法
田 野,练秋生
(燕山大学信息科学与工程学院,河北秦皇岛 066004)
基于重加权l1范数惩罚的远近场混合源定位算法
田 野,练秋生
(燕山大学信息科学与工程学院,河北秦皇岛 066004)
现有信源定位方法大多假定信源是远场源或近场源,而实际定位系统中往往存在远场源和近场源共存的情况.为实现远、近场源分离及高精度信源定位,本文在稀疏信号重构理论框架下提出了一种新的远近场混合源定位算法.该算法利用阵列协方差矩阵反对角线元素和重加权l1范数惩罚获得所有信源的到达角(Direction Of Arrival,DOA)估计.在DOA估计的基础上,根据远场与近场源距离参数位于不同区间的特点利用一维搜索实现远、近场源分离以及近场源距离参数的估计.从理论角度分析了重加权l1范数惩罚算法的重构性能.本文所提算法不仅同时适用于高斯和非高斯信号,而且无需多维搜索和参数配对,也无需信源数的先验信息,同时还可以获得较好的定位精度.计算机仿真结果验证了所提算法的有效性.
阵列信号处理;远场源;近场源;远近场混合源;重加权l1范数惩罚
1 引言
信源定位是阵列信号处理领域的主要研究内容之一,它在智能天线、雷达、声呐、麦克风阵列等领域有着广泛的应用并发挥着重要的作用[1],因此受到了国内外学者的广泛关注.受研究发展阶段和数学工具的限制,现有的信源定位方法大多假定信源为远场源或近场源.在该假设条件下,诸多信源定位方法被相继提出,包括适用于远场源定位的MUSIC算法[2,3]、ESPRIT算法[4,5]、子空间映射算法[6]及其改进算法;适用于近场源定位的2-D MUSIC算法[7]、高阶MUSIC算法[8]、高阶ESPRIT算法[9]、路径跟踪算法[10]以及线性预测算法[11]等.
然而,在一些实际的具体应用中,如表面波雷达定位[12]、基于麦克风阵列的说话人定位[13,14]以及室内指引(自导引)系统[15,16]中,往往只有一部分信源位于阵列的近场区域(即菲涅尔区域),而另一部分信源则位于阵列的远场区域,这将导致一种较为复杂的情况——远场源和近场源共存.在该背景下,已有的远场源和近场源定位方法均不再适用.
为解决远场源和近场源共存下的信源定位难题,Liang等人通过构建两个四阶累积量矩阵提出了一种两步MUSIC(two-stage MUSIC)算法[17],然而该算法计算复杂度高,且不适用于高斯信号.为攻克两步MUSIC算法的缺点,Jin和Wang等人分别基于二阶统计量提出了斜投影MUSIC(oblique MUSIC)算法[18]和混合阶MUSIC算法[19].上述远近场混合源定位算法均基于子空间理论,由于理论框架的限制其在信噪比较低、信源间距较近及信源数未知条件下,信源定位性能会因信号子空间与噪声子空间的不正确分离而产生较大的误差.
近年来,随着压缩感知理论体系[20,21]的出现和不断完善,作为其核心理论的稀疏信号重构引起了阵列信号处理领域研究者的广泛关注,从稀疏信号重构角度寻求解决子空间方法存在的共性问题成为了一种新的可能途径.鉴于此,Wang等人在文献[17]的基础上,提出了一种基于四阶累积量稀疏表示的远近场混合源定位方法[22],并获得了优于子空间类混合源定位方法的分辨率和定位精度.然而其自身存在的计算复杂度高、正则化参数选择不合理、需要信源数的先验信息以及不适用于高斯信号的缺陷也在一定程度上制约了算法的实用性.
针对上述远近场混合源定位方法存在的共性问题,本文提出了一种基于重加权l1范数惩罚的远近场混合源定位新方法.一方面,该算法基于二阶统计量稀疏表示,既适用于高斯信号又适用于非高斯信号;另一方面,基于重加权l1范数惩罚获得了更高的定位精度.此外,该算法不需要进行多维搜索和参数配对,也无需信源数的先验信息,实现简便.
2 远近场混合源模型
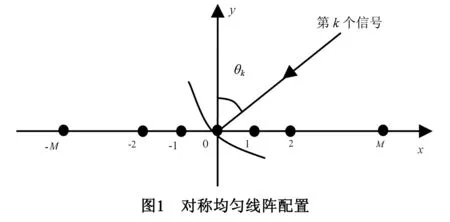
假设有K个信源信号(远场或近场)入射到一个由L=2M+1个阵元组成的对称均匀线阵上,如图1所示.以第0个阵元为相位参考点,则第m个阵元的输出可表示为
(1)
式(1)中,sk(t)代表第k个信源信号,nm(t)代表加性噪声,Q代表采样快拍数,τmk代表第k个信号到达第m个阵元和第0个阵元的时延差,表示为
τmk=mγk+m2φk
(2)
式(2)中,γk=-2πdsin(θk)/λ,φk=πd2cos2(θk)/λrk.θk和rk分别为第k个信源信号的DOA和距离,λ和d分别为载波波长和阵元间距.如果第k个信源为远场源,即rk→∞,则τmk简化表示为
τmk=mγk
(3)
基于以上分析,可得到远近场混合源信号接收模型为
y(t)=As(t)+n(t)
=AFsF(t)+ANsN(t)+n(t)
(4)
AF=[aF(γ1),…,aF(γK1)]
(5)
AN=[aN(γK1+1,φK1+1),…,aN(γK,φK)]
(6)
其中,K1和K-K1分别代表远场源和近场源的个数,aF(γk)和aN(γk,φk)分别为AF和AN的第k列,表示为
aF(γk)=[e-jMγk,…,1,…,ejMγk]T
(7)
aN(γk,φk)=[e-jMγk+M2φk,…,1,…,ejMγk+M2φk]T
(8)
sF(t)和sN(t)分别代表远场源和近场源信号向量,即
sF(t)=[s1(t),…,sK1(t)]T
(9)
sN(t)=[sK1+1(t),…,sK(t)]T
(10)
符号T代表转置操作.
本文做如下假设:
假设1 信源信号为零均值、相互独立的随机过程;
假设2 传感器上的加性噪声为零均值高斯白噪声,且与信源信号不相关,其方差为σ2;
假设3 为避免相位模糊,阵元间距和信源数分别满足d≤λ/4,K 3.1 所有信源的DOA估计 基于式(4),可得阵列协方差矩阵为 R=E{y(t)yH(t)}=ASA+σ2I (11) R的第p个反对角元素为 (12) 式(12)中,δ(·)代表狄拉克函数,p∈[1,L]. 对于所有p,本文构建如下L×1的向量 r =[R(1,L),R(2,L-1),…,R(L,1)]T =Bp+σ2iM+1 (13) 式(13)中 B=[b(γ1),…,b(γK)] (14) b(γk)=[e-j2Mγk,e-j2(M-1)γk,…,ej2Mγk]T (15) p=[P1,P2,…,PK]T (16) iM+1是L×1的向量,其第M+1个元素为1,其它元素为0. 当信源数K已知时,可直接通过最大似然估计获得噪声协方差的估计值,进而获得无噪观测模型.然而实际中信源数往往未知,为降低噪声干扰同时攻克信源数未知背景下的信源定位,本文通过去掉r的第M+1个元素(即噪声项)构建无噪观测模型,即 (17) (18) 进一步,所有信源的DOA估计可通过如下的最小l1范数惩罚问题获得 (19) 式(19)中,||·||2和||·||1分别代表l2范数和l1范数,h为权衡稀疏性与估计精度的正则化参数. 根据拉格朗日乘子法,式(19)可以等价表示为如下的约束形式 (20) 式(20)中,η为对应于h的新正则化参数. (21) (22) (23) (24) 式(24)中, (25) (26) 式(26)中,W=diag{w1,…,wN}为权值矩阵. (27) 在η≥α下通过消除噪声项有 (28) 由于权值wi≠0,式(26)可等价表示为 (29) 式(29)中,zN=WpN,z0=Wp0. (30) 对式(30)进行展开并根据|a+b|≥|a|-|b|有 (31) 式(31)中,ξ和ξc分别为p0中零值元素和非零元素的索引. (32) 即 (33) 基于以上分析,由式(23)获得的估计误差可被限制为 (34) 根据文献[23]的式(3.11)及其后续相关推导可得, (35) 证明完毕. 注1 定理1说明,重加权l1范数惩罚的应用可以很好地改善非零幅值估计精度,更有效地避免伪峰值的出现,从而保证了本文算法在信源数未知条件下的估计性能. 注2 pN中非零元素的个数和幅值即为信源数和信号功率,因此基于式(23)进行稀疏重构除获得DOA估计外,还可以获得较好的信源数估计和功率估计. 3.2 调整参数和正则化参数选择 调整参数ε和正则化参数h严重影响着算法的重构性能.然而,目前针对调整参数的选择还没有很好的策略,本文借鉴JLZA-DOA[27]和重加权l1范数惩罚[26]方法中的策略,通过大量仿真实验得到较为合理的调整参数,即经验上,ε=0.1min{Pk,k=1,…,K}是一个很好的选择. (36) 3.3 远、近场源区分及近场源距离估计 rs=[rNrF] (37) 其中,rN=[rN,1,…,rN,N1]∈[0.62(D3/λ)1/2,2D2/λ]为近场搜索区域,rF=[rF,1,…,rF,N2]为远场搜索区域,且rF,q>>2D2/λ(q=1,…,N2),D为阵列孔径. 然后通过式(38)的一维谱峰搜索区分远、近场源以及实现近场源距离估计 (38) 注3 重加权l1范数惩罚可以有效地抑制伪峰并获得较好的信源数估计,因此在算法实施过程中噪声子空间Un亦可较精确地得到. 注4 本文所提算法基于多维参数求解转化为多个一维参数分别求解的思想,即先利用稀疏重构估计所有信源的DOA,然后通过一维搜索区分远、近场源及实现近场源距离估计.整个过程无需多维搜索和参数配对过程. 3.4 计算复杂度分析 本文所提算法的计算复杂度主要集中于协方差矩阵构建过程、稀疏重构过程、交叉验证过程、远近场源区分及近场距离估计过程.第一项需要的复乘次数为O(L2Q),中间两项需要的复乘次数均为O(N3),最后一项需要的复乘次数为O(L2K(N1+N2)).作为对比,Wang等人提出的稀疏混合源定位方法[22]所需要的复乘次数主要为O(9L3Q)+O(K3N3+K6(N1+N2)3).通常N,N1,N2>>L>K,Q>>L>K,因此本文算法在信源数K或采样快拍数Q较大时,计算复杂度低于文献[22]的稀疏方法.注意到斜投影MUSIC算法[18]基于二阶统计量和子空间理论,所需要的复乘次数主要为O(L2Q)+O(L2N1(K-K1)),其计算复杂度低于本文所提算法,但需要说明的是本文算法无需信源数的先验信息且可获得改进的定位性能(详见仿真实验部分). 3.5 可估计的最大信源数分析 分析过完备基矩阵Φ可知,Φ的任意2M列是线性独立的.由唯一表示性质(URP)及文献[29]的定理1知,K 通过仿真实验验证所提算法的性能,并与两步MUSIC方法[17]、斜投影MUSIC方法[18]以及文献[22]的稀疏混合源定位方法进行比较.仿真中采用由9个阵元组成的对称均匀线阵,阵元间距d=λ/4,除实验1中的图2(b)外,信源信号均建模为ejζt,其中相位ζt均匀分布在[0,2π],噪声假定为高斯白噪声.DOA估计时,以1°间隔先对-90°到90°的空间进行粗网格划分,进而在估计出的角度周围逐步细化网格.DOA和距离估计的均方根误差(RMSE)通过500次独立的Monte Carlo仿真实验获得. 实验1 非高斯和高斯信号下的空间谱输出 信源信号位置分别为{θ1=-10°,r1=2.5λ},{θ2=20°,r2=∞},SNR和快拍数分别为10dB和200,两个信源信号的功率相等且P1=P2=1.非高斯和高斯信号下的空间谱输出结果分别如图2(a)和图2(b)所示.可以看出,本文算法不仅适用于高斯和非高斯信号,而且还可以获得较好的功率估计.这一结果也验证了定理1及注2的相关结论. 实验2 距离域远、近场源区分 仿真条件与实验1相同,近场搜索区域为[λ,8λ],搜索步长为0.1λ.远场搜索区域为[10λ,100λ],搜索步长为10λ.图3(a)为对应于θ=-10°的距离域空间谱输出结果,图3(b)为对应于θ=20°的距离域空间谱输出结果.可以看出θ=-10°对应的谱峰位于近场区域,而θ=20°对应的最大值位于远场区域,因此可判断信源1为近场源,信源2为远场源.实验2说明本文算法可以有效地区分远、近场源. 实验3 对假定信源数的敏感性分析 本文所提算法可无需信源数的先验信息,为验证这一结论.假定两个信源分别位于{θ1=10°,r1=3λ},{θ2=30°,r2=∞},SNR和快拍数分别为5dB和200,假定的信源数Ka由1变化到4,不同算法的空间谱输出分别如图4(a)~图4(d)所示.可以看出,只有本文所提算法不受假定信源数的影响,而其他方法均不同程度的受到影响,这充分说明了本文算法对假定信源数的高稳健性以及定理1与注1相关结论的正确性. 实验4 估计RMSE随SNR变化关系比较 信源信号位置分别为{θ1=10°,r1=2.5λ},{θ2=30°,r2=∞},信号功率相等,快拍数固定为200,SNR由-5dB变化到20dB,不同算法的RMSE随SNR的变化关系如图5所示.可以看出本文所提算法近场源DOA估计性能接近文献[22]的稀疏混合源定位方法,而优于两步MUSIC方法和斜投影MUSIC方法.远场源DOA估计性能接近斜投影MUSIC算法,而优于两步MUSIC方法和文献[22]的稀疏混合源定位方法.对于距离估计,本文所提算法则全面优于其他方法.此种现象可解释如下: 文献[22]的稀疏方法、斜投影MUSIC算法和本文算法分别在近场源DOA估计、远场源DOA估计和距离估计时更充分地利用了阵列输出数据(详见本文和参考文献[18,22]),因此它们在相对应场景下的参数估计精度最高.同时,相比于文献[22]的稀疏方法,本文算法由于采用了更好的惩罚策略以及更稳健的正则化参数也获得了相对较好的DOA估计性能. 实验5 估计RMSE随快拍数变化关系比较 SNR固定为10dB,快拍数由100变化到800,其他仿真条件与实验4相同.仿真结果如图6所示,与实验4得到的结论类似,本文所提算法近场源DOA估计性能优于两步MUSIC方法和斜投影MUSIC方法,远场源DOA估计性能优于两步MUSIC方法和文献[22]的稀疏混合源定位方法.对于距离估计,本文所提算法则全面优于其它方法.同时,还可以看到本文所提算法的RMSE随快拍数的增加而明显降低. 实验6K>2时的空间谱输出及运算时间比较 考虑两个近场源和一个远场源信号入射情况,信源位置分别为{θ1=-10°,r1=2λ},{θ2=20°,r2=3λ},{θ3=60°,r3=∞},SNR和快拍数分别为20dB和200,三个信源信号的功率相等且P1=P2=P3=1,运行程序的计算机配置为英特尔酷睿i5 1.8GHz处理器,内存为2GB.非高斯信号下本文算法和文献[22]的稀疏混合源定位方法的空间谱输出和运算时间如图7所示.可以看出,本文算法不仅适用于K>2时的远近场混合源定位场景,而且和文献[22]的稀疏混合源定位方法相比,还获得了估计精度与算法复杂度的良好平衡. 本文在稀疏信号重构理论框架下提出了一种新的远近场混合源定位算法.该算法充分利用了二阶统计量和重加权l1范数惩罚的优势,不仅适用于高斯和非高斯信号,而且无需多维搜索和参数配对过程,也无需信源数的先验信息.进一步借助合理的调整参数和正则化参数更是获得了较高的DOA、距离和功率估计表现. [1]Krim H,Viberg M.Two decades of array signal processing research:the parametric approach[J].IEEE Signal Processing Magazine,1996,13(4):67-94. [2]Schmit R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation,1986,34(3):276-280. [3]Wang Q,Wang L,An K,et al.DOA estimation of smart antenna signal based on MUSIC algorithm[J].Journal of Networks,2014,9(5):1309-1316. [4]Roy R,Kailath T.ESPRIT-a subspace rotation approach to estimation of parameters of cissoids in noise[J].IEEE Transactions on Acoustic,Speech and Signal Processing,1986,34(10):1340-1342. [5]Ma Y,Chen B,Yang M,et al.A novel ESPRIT-based algorithm for DOA estimation with distributed subarray antenna[J].Circuits,Systems,and Signal Processing,2015,34(9):1-22. [6]王军,闫锋刚,金铭,等.基于噪声子空间映射的二维波达角快速估计算法[J].电子学报,2015,43(2):276-282. Wang J,Yan F G,Jin M,et al.Efficient algorithm for 2-D DOA estimation based on noise subspace mapping[J].Acta Electronica Sinica,2015,43(2):276-282.(in Chinese) [7]Huang Y D,Barkat M.Near-field multiple source localization by passive sensor array[J].IEEE Transaction on Antennas and Propagation,1991,39(7):968-975. [8]梁国龙,韩博.基于互素对称阵的近场源定位[J].电子与信息学报,2014,36(1):135-139. Liang G L,Han B.Near-field sources localization based on co-prime symmetric array[J].Journal of Electronics & Information Technology,2014,36(1):135-139.(in Chinese) [9]Yuen N,Friedlander B.Performance analysis of high order ESPRIT for localization of near-field sources[J].IEEE Transactions on Signal Processing,1998,46(3):709-719. [10]Starer D,Nehorai A.Passive localization of near-field sources by path following[J].IEEE Transactions on Signal Processing,1994,42(2):677-680. [11]Grosicki E,Abed M K,Hua A.A weighted linear prediction method for near-field source localization[J].IEEE Transactions on Signal Processing,2005,53(10):3651-3660. [12]Cirillo L A,Zoubir A M,Amin M G.Estimation of near-field parameters using spatial time-frequency[A].Proceedings of the IEEE International Conference on Acoustics,Speech and Signal Processing[C].USA:IEEE Press,2007.1141-1144. [13]Arslan G,Sakarya F A,Evans B L.Speaker localization for far-field and near-field wideband sources using neural networks[A].Proceedings of the IEEE EURASIP Workshop on Nonlinear Signal Image Processing[C].Antalya,Turkey:IEEE Press,1999.528-532. [14]Mukai R,Sawada H,Araki S,et al.Frequency-domain blind source separation of many speech signals using near-field and far-field models[J].EURASIP Journal on Applied Signal Processing,2006,Article ID 83683:1-13. [15]Argentieri S,Danes P,Soueres P.Modal analysis based beamforming for nearfield or farfield speaker localization in robotics[A].Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems[C].Beijing,China:IEEE Press,2006.866-871. [16]Kennedy R A,Ward D B,Thushara P,et al.Nearfield beamforming using nearfield/farfield reciprocity[A].Proceedings of the IEEE International Conference on Acoustics,Speech and Signal Processing[C].USA:IEEE Press,1999.3741-3744. [17]Liang J L,Liu D.Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J].IEEE Transaction on Signal Processing,2010,58(1):108-120. [18]He J,Swamy M N S,Ahmad M O.Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources[J].IEEE Transaction on Signal Processing,2012,60(4):2066-2070. [19]Wang B,Zhao Y,Liu J.Mixed-order MUSIC algorithm for localization of far-field and near-field sources[J].IEEE Signal Processing Letters,2013,20(4):311-314. [20]Candès E J,Wakin M B.An introduction to compressive sensing[J].IEEE Signal Processing Magazine,2008,25(2):21-30. [21]王强,李佳,沈毅.压缩感知中确定性测量矩阵构造算法综述[J].电子学报,2013,41(10):2041-2050. Wang Q,Li J,Shen Y.A survey on deterministic measurement matrix construction algorithms in compressive sensing[J].Acta Electronica Sinica,2013,41(10):2041-2050.(in Chinese) [22]Wang B,Liu J J,Sun X Y.Mixed sources localization based on sparse signal reconstruction[J].IEEE Signal Processing Letters,2012,19(8):487-490. [23]Donoho D L,Elad M,Temlyakov V N.Stable recovery of sparse overcomplete representations in the presence of noise[J].IEEE Transactions on Information Theory,2006,52(1):6-18. [24]Zheng C,Li G,Zhang H,et al.An approach of DOA estimation using noise subspace weighted l1minimization[A].Proceedings of the IEEE International Conference on Acoustics,Speech and Signal Processing[C].USA:IEEE Press,2011.2856-2859. [25]Fan J,Li R.Variable selection via nonconcave penalized likelihood and its oracle properties[J].Journal of the American Statistical Association,2001,96(456):1348-1360. [26]Candès E J,Wakin M B.Enhancing sparsity by reweighted l1minimization[J].Journal of Fourier Analysis and Applications,2006,101(476):1418-1429. [27]Hyder M M,Mahata K.Direction-of-arrival estimation using a mixed l2,0norm approximation[J].IEEE Transactions on Signal Processing,2010,58(9):4646-4655. [28]Shao J.Linear model selection by cross-validation[J].Journal of the American Statistical Association,1993,88(422):486-494. [29]Gorodnitsky I F,Rao B D.Sparse signal reconstruction from limited data using FOCUSS:A re-weighted minimum norm algorithm[J].IEEE Transactions on Signal Processing,1997,45(3):600-616. 田 野 男,1985年12月生于河北省平泉县,2014年于吉林大学通信与信息系统专业获得博士学位,现为燕山大学信息科学与工程学院讲师,主要研究方向为阵列信号处理、稀疏信号重构等. E-mail:tianye@ysu.edu.cn 练秋生 男,1969年8月生于江西遂川,工学博士,现为燕山大学信息科学与工程学院教授、博士生导师,主要研究方向为稀疏表示,压缩感知等. E-mail:lianqs@ysu.edu.cn Mixed Far-Field and Near-Field Source Localization Algorithm Based on Reweighted l1-Norm Penalty TIAN Ye,LIAN Qiu-sheng (SchoolofInformationScienceandEngineering,YanshanUniversity,Qinhuangdao,Hebei066004,China) Existing source localization methods mostly assume that the sources are pure near-field sources or pure far-field sources.While in practical localization systems,both far-field and near-field sources may exist simultaneously.To classify far-field and near-field sources,and also to achieve high-precision source localization,a novel mixed far-field and near-field source localization algorithm is proposed in sparse signal reconstruction framework.The algorithm first utilizes anti-diagonal elements of array covariance matrix and reweighted l1-norm penalty to obtain DOA estimation of all sources,then classifies far-field and near-field sources and successively obtains range estimation of near-field sources via one-dimensional search,by exploring the feature that the range parameters of far-field and near-field sources are located in different areas.Theoretically,we analyze the reconstruction performance of the reweighted l1-norm penalty algorithm.The proposed algorithm is not only suitable for dealing with Gaussian signals and non-Gaussian signals,but also without multi-dimensional search and parameter pairing process,and also without knowing the number of sources.Meanwhile,the proposed algorithm can even provide good estimation accuracy.Computer simulation results validate the effectiveness of the proposed algorithm. array signal processing;far-field sources;near-field sources;mixed far-field and near-field sources;reweighted l1-norm penalty 2015-04-22; 2015-08-17;责任编辑:孙瑶 国家自然科学基金(No.61471313,No.61601398);河北省自然科学基金(No.F2016203100,No.F2014203076);河北省高等学校青年拔尖人才计划(No.BJ2016051) TN911.7 A 0372-2112 (2016)10-2440-09 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.10.0233 远近场混合源定位算法









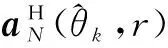
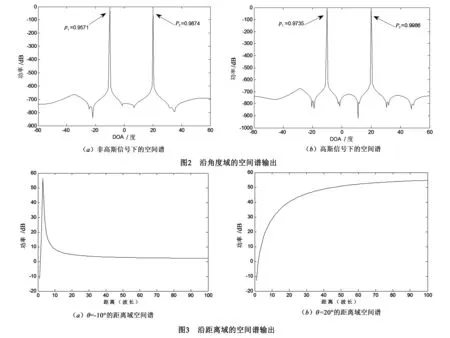
4 仿真实验
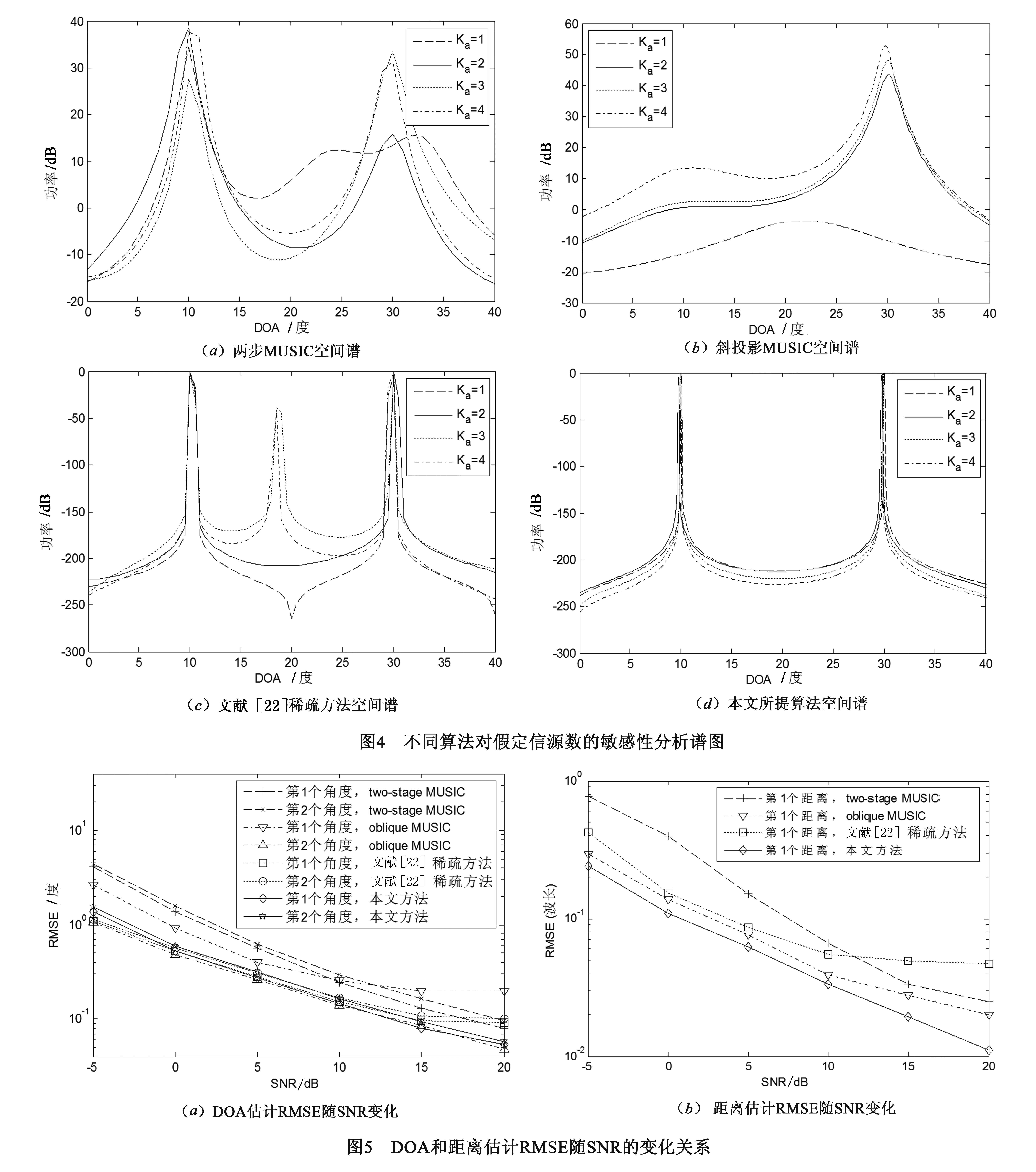

5 结论


——以鲁甸地震相关新浪微博为例

