各类最值问题的“共性”与“个性”

■黄　莉

各类最值问题的“共性”与“个性”

■黄莉

近年来，中考题中最值问题从未缺席。最值问题，既有“共性”，也有“个性”。本文结合一些典型例题，将它们转化为相应的数学模型进行分析解决。

最小值最短路径最大利润

类型一：求有共同端点的线段之和最小值或三角形周长最小值问题

例1如图1，直线l同侧有两点A、B，已知A、B到直线l的垂直距离分别为1和3，两点的水平距离为3，要在直线l上找一个点P，使PA+PB的和最小。请在图中找出点P的位置，并计算PA+PB的最小值。

例2如图2，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD上移动，则PE+PC的最小值是_____。

例3如图3，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN＝30°，B为AN弧的中点，P是直径MN上一动点，则PA＋PB的最小值为（）。

例4如图4，在Rt△ABC中，∠C=90°，∠B= 60°，点D是BC边上的点，CD=1，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是_____。

图1

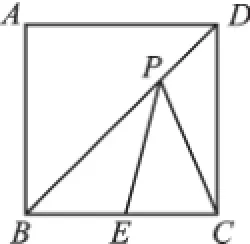
图22

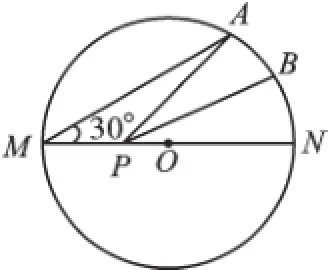
图3

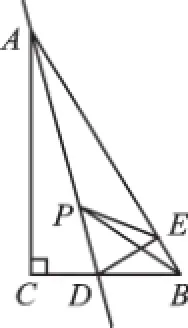
图4

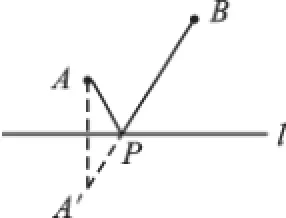
图1-1

图2-12-1

图3-1

图4-1

例1要求PA+PB的最小值，也就是求A、B两点到同一点的和的最小值，当点P在这两点之间，且三点共线时它们的距离之和最小，即：两点之间线段最短。而由于A、B两点在所要找的直线上点的同一侧，因此想到作其中任一点（A）关于这条直线的对称点（A′），则l就是线段AA′的对称轴，如图1-1，根据对称轴上任一点到线段的两个端点距离相等，从而转化成在直线l上找一点到A′（A的对称点）与另一点B的距离之和最小值，于是自然想到连接A′B，A′B与直线l的交点就是所求的P点，再通过构造的直角三角形，利用勾股定理计算线段A′B即可。

例2中的正方形正好是轴对称图形，BD就是其一条对称轴，因此直接找到C点关于BD的对称点A，从而直接连接AE，如图2-1，再在Rt△ABE中，利用勾股定理求出AE即可。

例3中的圆也是轴对称图形，直径MN就是其一条对称轴，因此找到B点关于MN的对称点C，从而连接AC，如图3-1，借助圆中同弧所对的圆周角与圆心角的关系及垂径定理的内容，可知∠AOC＝90°，巧妙构造Rt△OAC，根据题意，运用勾股定理可求出AC=，所以PA+PB的最小值为2。

例4虽然是求三角形周长最小值，但由于其中的BE是定值，所以此题实质就是求PC+PB的最小值。而此题的翻折就有轴对称图形，E点就和C点关于AD对称，因此只要求BC的值，再加上BE的值即可，如图4-1。

因此这一类题目的“共性”就是构建“对称模型”，实现转化，再根据“两点之间线段最短”求出最小值。

拓展延伸：蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食的最短路径问题。

例1如图5，有一个虫子想从点A沿棱长为1cm的正方体表面爬到点B，求它爬过的最短路程。

例2图6是一块长、宽、高分别是6cm,4cm和3cm的长方体木块。一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是_____。

例3如图7，已知圆柱底面的周长为4dm，圆柱高为2dm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为。

图5

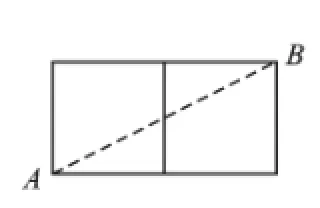
图5-1

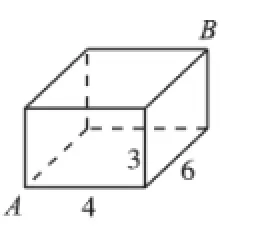
图6

图6-1

图6-2

图6-3

图7

图7-1

图8

图8-1

例1要求虫子沿正方体表面爬过的最短路程，需要在从A点到B点的侧面展开图上找出，因此画出其侧面展开图，直接利用勾股定理计算出线段AB的长度即可。也是利用两点之间线段最短。

例2是求长方体表面的最短路程，看似和正方体差不多，但是要注意，它们虽然有“共性”，但是又有其“个性”，正方体的每个面展开都是全等的正方形，而长方体由于长、宽、高各不相同，它的每个面展开也不一样（如图6-1，6-2，6-3），因此要注意根据边的长度，由勾股定理求出长度，再去判断出最短的距离。

例3要求金属丝的长，也需将圆柱的侧面展开得到长方形（如图7-1），找准A、C两点，再根据勾股定理计算即可。

例4求蚂蚁沿圆锥表面爬过的最短路程，也是将其侧面展开得到扇形（如图8-1），根据题意求出AM的距离即可。

因此这一类题目的“共性”就是利用其侧面展开图，将立体图形转化为平面图形，从而再根据“两点之间线段最短”求出最小值。

类型二：二次函数中的最值问题

例1求函数y=x2-2x-3的最大值和最小值。

例2变式：当-2≤x≤2时，求函数y=x2-2x-3的最大值和最小值。

例3变式：当1≤x≤2时，求函数y=-x2-x+1的最大值和最小值。

这一类是单纯的求二次函数的最值问题，它们主要根据自变量的取值范围不同，作出函数草图如下，在所给自变量范围内，观察图像的最高点和最低点，由此得到函数的最大值、最小值及函数取到最值时相应自变量x的值。

例2

例3

拓展延伸：实际问题中的二次函数最值问题

例1某商场以每件30元的价格购进一种商品，试销中发现这种商品每天的销售量m（件）与每件的销售价x（元）满足一次函数m=162-3x，30≤x≤54。

（1）写出商场卖这种商品每天的销售利润y与每件销售价x之间的函数关系式；

（2）若商场要想每天获得最大销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？

例2已知在△ABC中，边BC的长与BC边上的高的和为20。

（1）写出△ABC的面积y与BC边的长x之间的函数表达式，并求出面积为48时BC边的长；

（2）当BC多长时，△ABC的面积最大？最大面积是多少？

这一类题的“共性”是将实际问题转化成数学问题——利用二次函数的知识来解决，并且此类构建最值问题，主要有两种形式，一是商品经营活动中的求最大利润、最大销量等问题，解此类问题的关键是通过题意及现实数量关系，确定出相关函数的表达式：

y=（x-30）（162-3x）=-3x2+252x-4860，

30≤x≤54。

另一类是几何图形中有关面积的最值问题，解这类问题关键是要掌握图形面积的求解与表示，构建相应的函数关系式：

最后观察其“个性”，根据函数图像的增减性确定其最值，并注意问题的实际意义。

最值问题是初中阶段的常见问题，这类试题内容丰富，涉及面广，解法灵活多样，而且具有一定的难度。因此我们需要根据具体问题，找到其“共性”，将其转化为相应的数学模型，再根据“个性”解决。并且将生活中的经济问题与数学中的最值问题联系起来，以达到最高效率。

（作者为江苏省徐州市第三十六中学教师）