以“静”制“动”化“繁”为“简”——有感于“垂线段最短”在数学动点问题中的运用

■王永锋

以“静”制“动”化“繁”为“简”——有感于“垂线段最短”在数学动点问题中的运用

■王永锋

垂线段是初中几何的一个基础知识。《初中数学新课程标准（2011年版）》对这方面的内容提出过明确要求：理解垂线、垂线段等概念，能用三角尺或量角器过一点画已知直线的垂线；理解点到直线的距离的意义，能度量点到直线的距离。在这里，必须要指出的是：连接直线外一点与直线上各点的所有线段中，垂线段最短，这条垂线段的长度，叫做点到直线的距离。

2011年的苏科版教材把这一内容放在初一上学期第6章第5节，尽管考查的知识较为基础，但由于七年级学生对几何语言的表述不甚规范，仍然会出现一些认知上的偏差。同时，由于教师对本节知识的重要性不够重视，笼统地认为这部分内容考试考得太少，不需花大力气去讲，因而在引导学生规范作图和表述上不甚到位，达不到应有的教学水准。实际上，八、年级教学时，常常会碰到许多让广大学生“动”色变的动点问题，这种问题形式上较为琐，旨在考查学生的悟性，特别是经常会利用“垂线段最短”把过程中的“动”转化为某一时刻的“静”，把一个复杂的问题转化为一个较为简单的问题。教师教学时可以尝试从以下几个方面来理解垂线段最短。

一、垂线段最短是一个知识点

垂线段最短是学生应该掌握的重要知识，它本身是一个知识点。学生通过从身边熟悉的事物中选取学习素材认识了垂直，进而了解了垂线段，并通过两个定义的对比理解了垂线和垂线段的联系和区别，最后再根据直线外一点和直线画出垂线，并找出、标记好垂线段。

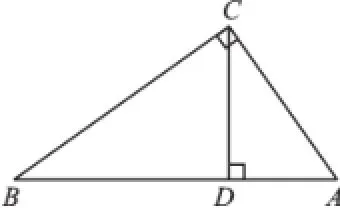
图1

例1如图1，AC⊥BC，C为垂足，CD⊥AB，D为垂足，BC=8，CD=4.8，BD=6.4，AD=3.6，AC=6，那么点C到AB的距离是_______，点A到BC的距离是_______，点B到CD的距离是_______，A、B两点的距离是_______。

解：C到AB的距离是垂线段CD的长度，为4.8，同理，中间两空分别为6和6.4，而A、B两点的距离是线段AB的长度，即为10。

例2如图2，污水处理厂A要把处理过的水引入排水沟l，应如何铺设排水管道才能使排水沟最短，请你在图纸上画出铺设管道的路线，并请你思考为什么这样画。

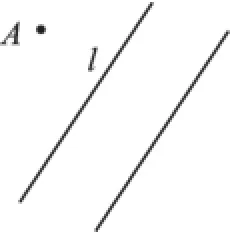
图2

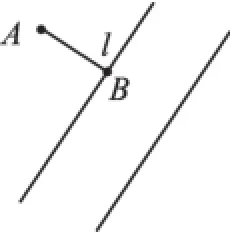
图3

解：如图3，过点A作垂线段AB交l于点B，理由是垂线段最短。

评析：例1主要是考查学生的辨析能力；点和线之间的距离是垂线段的长度，两个端点是点和垂足，点和点之间的距离是两点所连线段的长度；例2就是利用垂线段最短，但要注意画垂线段的方法。

知识是能力的先导。只有把知识真正学到位，对概念和性质理解通透，才能真正转化为能力，为后续总结方法、提炼思想和形成经验做好铺垫。

二、垂线段最短是一条方法线

在解决动点问题的过程中，垂线段就是好多学生一道绕不过的坎，许多疑难题目通过作垂线段，便能迎刃而解。可以说，它为解决某些数学问题提供了一条明朗的方法线。

例3如图4，⊙O的直径为10cm，弦AB为8cm，点P是弦AB上的一动点。若OP的长为整数，则满足条件的点P有（）

A.2个B.3个

C.4个D.5个

图4

解：当P与A或者B重合时，OP最大值为5，当OP与AB垂直时，由垂径定理和勾股定理，求得OP最小值为3，在3和5之间还有2个长度为4的点，从而选D。

例4据气象台预报，一股强台风的中心位于宁波（指城区，下同）东南方向千米的海面上，目前台风中心正以20千米/时的速度向北偏西60°的方向移动，距台风中心50千米的圆形区域均会受到强袭击。已知宁海位于宁波正南方向72千米处，象山位于宁海北偏东60°方向56千米处。请问：宁波、宁海、象山是否会受这次台风的强袭击？如果会，请求出受强袭击的时间；如果不会，请说明理由。（为解决问题，需画出示意图，现已画出其中一部分，如图5，请根据需要，把图形画完整）

图5

图6

解：如图6，过点P作水平直线与AB的延长线交于点O，延长台风中心移动射线PQ与AO交于M。在Rt△AOP中，求得AO=OP=36得BO=36+36；由∠OPM=30°，得MO=36+ 36=BO，故M与B重合，台风中心必经过宁海，时间为5小时；C为象山，C到PQ距离CN=28，故象山会受到影响，求影响时间可以先求以C为圆心，50km为半径的圆与PQ相交的弦长为，时间为h；A到PQ距离AD=AB，sin60°=36，故宁波不受影响。

评析：对于例3，学生能够感受到在P从A到B运动的过程中，OP的长度先变小后变大，从而考虑到关键是求出最小长度与最大长度。部分学生对本题转化的方法掌握不够灵活，导致猜答案的现象较为普遍。教师在讲解本题后，还可以设计以下问题：

（1）⊙O的直径为10cm，OP=4cm，则过点P最长的弦长度是______，最短的弦长度是_____；

（2）⊙O的直径为10cm，OP=4cm，过点P的弦中，长度为整数的弦有_____条。

例4考查学生的画图能力，同时也让学生明确城市可作为图形中的一个点，而台风走的是一条线，应该把问题中的“是否会影响”转化为求“最短距离问题”，从而想到比较垂线段和半径的大小问题，于是把该题目转化为解直角三角形问题解答。

由此可见，在数学的动点问题中，“垂线段最短”可以为解决问题提供一种有力工具。通过找寻“静止”时符合要求的那一瞬间，便可提高解题的准确率。

三、垂线段最短是一层思想面

我们平时的教学工作中一直存有这个问题：学生题目做得不少，可只要条件稍稍一变，一些学生考试时就会不知所措，特别是对蕴含在其中的规律，更是迟迟不能领会。其实，对于有些动点问题，可以利用题目中显见的结论，找出其中蕴含的思想，进而转化为熟知的问题来解决。

例5如图7，⊙O的半径为2，点O到直线l的距离为3，点P是直线l上的一个动点，PQ切⊙O于点Q，则PQ的最小值为（）

C.3D.5

图7

图8

图9

评析：上述两个例题都是以切线为载体构造直角三角形的动点问题，其三边长度满足勾股定理，而其中一边已知大小，要求某一边的最小值，便可转化为求第三边的最小值。如果想不到这种化归思想，学生便不会找到利用“垂线段最短”得到满足条件时的“静止”的那一刻，也便不能圆满解决问题。

在解决动点问题的过程中，教师应把更多的精力花在诱导学生怎样去想、怎样去悟上来，要置数学思想方法的运用于解题的核心位置，充分发挥数学思想的解题功能。如果学生能在解决问题的过程中充分发挥数学思想方法的指导功能，利用其中蕴含的结论进行转化，不仅可少走弯路，而且可以大大提高其数学能力。

四、垂线段最短是一种经验体

学生学习一定的数学基础知识，领会一系列的思想方法后，便会在解决问题的过程中慢慢积累一些解题经验。这些经验既可以让学生独立解决一些常见的问题，又可以让学生在具体情境下灵活分析问题，形成一种知识、方法与思想融汇的数学体系，提升数学素养。

例7（2014·广西贵港）如图10，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线。若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（）

图10

图11

评析：本题隶属于双动点问题，要求学生在进行思考时考虑到“将军饮马问题”和角的轴对称性，进而转化为作对称点E，于是便得到PC= PE，进而求PE+PQ的最小值，当且仅当三点共线时有最小值为EQ，进而再转化为求EQ的最小值，此时应利用“垂线段最短”，再根据等腰三角形ACE腰上的高相等，最后再利用直角三角形面积求出答案。可以说，圆满解决本题需要学生具备一些必要的思想方法，并要有一定的解题经验，这种以静制动的策略值得学生多回味思索。

（作者为江苏省苏州市吴江区盛泽第二中学教师）