巧用数学思想方法学习一元一次方程

何春华

巧用数学思想方法学习一元一次方程

何春华

数学思想方法是数学的灵魂，是解决数学问题的金钥匙.一元一次方程的知识中蕴含了许多数学思想方法，大家在掌握基础知识的同时，还应注意对数学思想的提炼、总结，从而提高解题的能力.下面，我们举例分析一元一次方程内容中的方法策略，供同学们参考.

一、三个基本思想+一个解题策略

1.整体思想

当一个问题中未知数较多，逐个求解比较复杂，或不能求解时，可将其中满足某一共同特性的式子看作一个整体求解.这样既便于列方程，又便于解方程.

【分析】本题可以直接去括号求解，但似乎有点繁琐，如果将（7x-5）看作一个整体，则求解时能更方便些.

【点评】有些方程，可以将一部分式子联系起来，先看成一个整体，把方程看成这个整体的一元一次方程，从而减少了方程的项数，使求解简便.

例2有一个八位的电话号码，前四位数字完全相同，从第四位到第八位是依次减小的连续自然数，全部数字之和恰好等于号码的最后两位数字组成的两位数（两位数字的前后顺序不变），请写出这个电话号码.

【分析】本题前四位数字完全相同，且它们与后四位数字有联系，不妨将前四位数字设出来，这样便于列方程求解.

解：设前四位数字均为x，则后四位数字依次为x-1，x-2，x-3，x-4.

由题意得：4x+x-1+x-2+x-3+x-4=10（x-3）+x-4，解得x=8.

所以x-1=7，x-2=6，x-3=5，x-4=4，

答：这个电话号码是88887654.

【点评】本题若逐个设出各位数字，则未知数过多，不易列出方程，但从整体考虑，视前四位数字为一个整体，则方便简捷.希望同学们能认真体会.

2.转化思想

转化思想就是将复杂的问题转化为简单的问题，将生疏的问题转化为熟悉的问题，将未知化为已知.解一元一次方程就是将方程的最终形式转化为“x=a”.

【分析】本题分母中出现小数，给解方程带来了麻烦，通过观察发现，其分子也有小数，可利用分数的基本性质，将分子分母都乘10，化简方程求解.

去分母，得3（4x+9）=5（2x+3）+15.

去括号，得12x+27=10x+15+15.

移项，得12x-10x=15+15-27，

【点评】本章的转化思想主要体现在将复杂的一元一次方程通过去分母、去括号等过程，转化为一元一次方程的最简形式求解，以及将实际问题转化为用一元一次方程求解.

3.分类讨论思想

分类讨论思想，是一种把问题中可能出现的多种情况分类讨论进而解决问题的策略，运用这种策略可完整获取问题的答案.

例4A、B两地相距450千米，甲、乙两车分别从两地同时出发，相向而行.若甲车的速度是120千米/时，乙车的速度是80千米/时，问经过多长时间甲、乙两车相距50千米？

【分析】题目中甲、乙两车相距50千米，有两种可能：一种是两车相遇前两车相距50千米，另一种是两车相遇后，再行驶一段时间，两车还会相距50千米，所以本题应分两种情况讨论.

解：设经过x小时两车相距50千米.

若两车相遇前相距50千米，由题意得：120x+80x=450-50，解得x=2；

若两车相遇后相距50千米，由题意得：120x+80x=450+50，解得x=2.5.

答：经过2小时或2.5小时两车相距50千米.

【点评】本章中的分类讨论思想主要体现在解决实际应用问题上，如行程类问题中对位置、距离的分类讨论，公园售票时根据人数不同而售价不同时的分类讨论，希望同学们能注意收集并整理涉及这类数学思想的内容.

4.挖掘隐含条件

例5在长方形ABCD中，放入六个形状、大小相同的长方形，所标尺寸如图所示，求小长方形的长和宽.

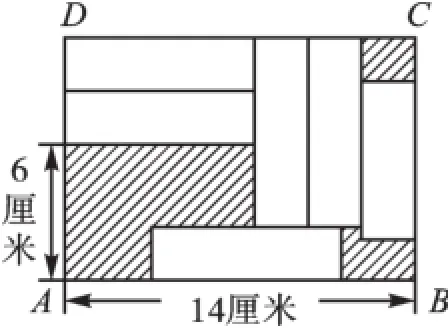
【分析】观察图形可知有如下两个数量关系：①小长方形的长+3个小长方形的宽= 14cm；②2个小长方形的宽+6cm=小长方形的长+1个小长方形的宽.我们借助①设出未知数，根据②列出方程求解.

解：设小长方形的宽为xcm，则小长方形的长为（14-3x）cm，由题意可得：2x+6=（14-3x）+ x，解得x=2，所以14-3×2=8.

答：小长方形的宽为2cm，长为8cm.

【点评】本题通过观察、分析，将隐含在图形中的数量关系挖掘出来，即将图形的有关信息转化为数量关系，进而列出方程解决问题.

二、设元的三个方法

1.直接设未知数

当题目中的数量关系能用所求的未知量表示时，不妨直接设未知数，即求什么设什么，这是设未知数常用的方法.

例6某学校组织学生去秋游，从学校出发去风景点A参观游览，在A风景点停留1小时后，又绕道去风景点B，再停留半小时后返回学校，去时的速度是5千米/时，回来的速度是4千米/时，来回（包括停留时间在内）共用去6小时30分钟.回来时因为绕道关系，路程比去时多2千米，求去时的路程.

【分析】本题看起来比较麻烦，分析后发现，题目里要求的只有一个未知量，就是去时的路程.题目的等量关系是：去时的时间+回来的时间+停留时间=共用的时间，以上“量”都可以用去时的路程表示.

解：设去时的路程为x千米，那么回来时的路程为（x+2）千米，去时路上所需时间为小时，回来时路上所需时间为小时.

解得x=10.

答：去时的路程为10千米.

【点评】本题抓住了“去时的路程”与“各个时间”的关系，直接设出未知数，问题顺利得解，看来，分析题目中的数量关系是解题的关键.

2.间接设元

即所设的不是所求的，适当选择与所求的未知数有关的某个量为未知数，则易找出符合题意的数量关系，从而得到方程.

例7李伟从家里骑摩托车到火车站，如果每小时行30千米，那么比火车开车时间早到15分钟；若每小时行18千米，则比火车开车时间迟到15分钟.现在李伟打算在火车开车前10分钟到达火车站，求李伟此时骑摩托车的速度应该是多少？

【分析】本题中所求值，不容易直接从中寻找关系，但注意从家到火车站的路程和距火车开车的时间为定值，这时可以用“退一步”的方式先求出某定量，则其他关系就会迎刃而解.

解：设李伟家到火车站的路程为x千米，则由火车开车时间固定这一等量关系，可简便得

答：李伟此时骑摩托车的速度为27千米/时.

【点评】本题利用火车“规定”的时间为相等关系建立方程求解，属于间接设未知数的方法，希望同学们认真体会这种解题思想.

3.辅助设元

在一些较复杂的实际问题中，当出现的未知量较多，并且有时看起来似乎缺少条件时，可考虑设辅助未知数，在已知条件和所求解的问题之间“牵线搭桥”，从而能顺利找出等量关系并列出方程.一般来说，辅助未知数设而不求，在解题过程中会自行消去.

例8某公司生产普通汽车和新能源汽车，该公司在去年的汽车产量中，新能源汽车占总产量的10%，今年由于国家能源政策的导向和油价上涨的影响，计划将普通汽车的产量减少10%，为保持总产量与去年相等，求今年新能源汽车的产量应增加的百分数.

【分析】在求解今年新能源汽车的产量应增加的百分数时，需要的是去年的汽车生产总量.因此设今年新能源汽车的产量应增加的百分数为x的同时，还应设去年的汽车生产总量为a，根据“今年总产量与去年相等”列出方程求解.

解：设去年的总产量为a，今年新能源汽车的产量应增加的百分数为x，则去年普通汽车和新能源汽车的产量分别为90%a和10%a，今年的普通汽车和新能源汽车的产量分别为90%a（1-10%）和10%a（1+x），根据题意列方程，得90%a（1-10%）+10%a（1+x）=a，解得x= 0.9=90%，所以今年新能源汽车的产量应增加的百分数为90%。

【点评】对于一些较复杂的问题，往往条件隐含关系交错.这时不妨引入辅助未知数，在已知量和未知量之间架起一座“桥梁”，方便理顺各个量之间的关系，列出方程.而所设辅助未知数在解题过程中会被消去，即满足辅助未知数“设而不求”的特点.

（作者单位：江苏省海门市实验初级中学）