勾股定理的起源与发展
顾金峰
勾股定理的起源与发展
顾金峰

email:czsshy@126.com
勾股定理是数学的一个基本定理,是几何学中的明珠,既重要又简单.其简单表述为:直角三角形两直角边的平方和等于斜边的平方.
关于勾股定理的起源,各国各民族都有不同的记载.据西方的文字记载,毕达哥拉斯于公元前550年发现了该定理.在中国,西汉的数学著作《周髀算经》中记录的商高同周公的一段对话描述了勾股定理的由来,由于勾股定理的内容最早见于商高的话语中,所以人们也把这个定理叫做“商高定理”.看来,我国古代的人民早在几千年以前就已经发现并应用勾股定理了.
关于勾股定理的名称,在我国,以前叫毕达哥拉斯定理,这是随西方数学传入时翻译的名称.20世纪50年代,学术界曾展开过关于这个定理命名的讨论,最后用“勾股定理”,得到教育界和学术界的普遍认同.1993年,全国自然科学名词审定委员会公布数学名词,确定这一定理的汉文名称为勾股定理,其对应的英文名是Pythagoras theorem,注释中说:“又称‘毕达哥拉斯定理’.曾用名‘商高定理’.”至此,“勾股定理”成为我国确立的标准名称.
勾股定理在几何学中,充满着无限魅力,千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至还有国家总统.1940年,一本名为《毕达哥拉斯命题》的勾股定理的证明专辑出版了,其中收集了367种不同的证明方法.实际上还不止这么多,有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了20多种精彩的证法.这是任何定理无法比拟的.在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名.下面我们就来介绍一下其中的4种著名的勾股定理证法.
法1——弦图法
用四个全等的直角三角形可以拼成如图1所示的大正方形,这个图形被称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的.弦图中每一个直角三角形涂朱色,它们的面积叫做“朱实”,中间的一个小正方形涂黄色,它的面积叫做“中黄实”,也叫“差实”,以弦为边的大正方形面积叫做“弦实”,“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实.”也就是
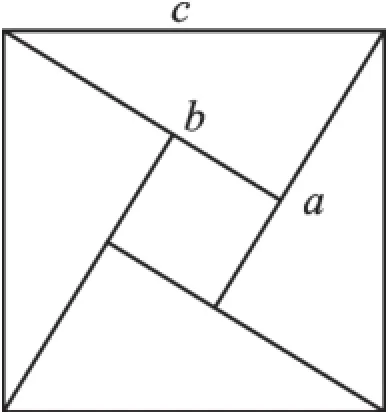
图1
法2——面积剖分法
据传这是当年毕达哥拉斯发现勾股定理时做出的证明.用四个全等的直角三角形可以拼成图2,也可以拼成图3,这两个大正方形的边长都为(a+b),面积相等.把这两个图形中的四个直角三角形除去后,剩余部分的面积应该相等,即图2中的c2等于图3中a2与b2的和,也就是a2+b2=c2.
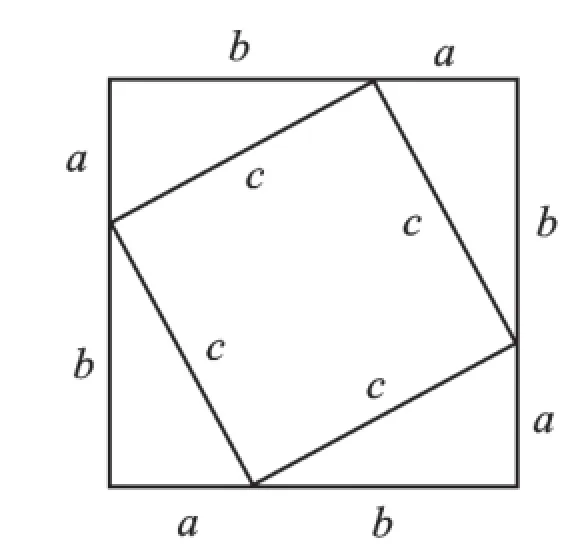
图2
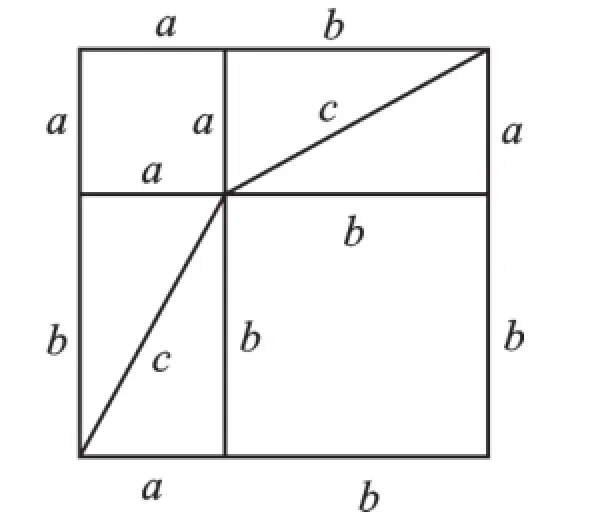
图3
法3——总统证法
1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德.他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨.好奇心使然,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么.只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形.于是伽菲尔德便问他们在干什么,那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答道:“是5呀.”小男孩又问道:“如果两条直角边长分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不假思索地回答道:“那斜边的平方一定等于5的平方加上7的平方.”小男孩又说:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心里很不是滋味.于是,伽菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题.他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法.
如图4,梯形由三个直角三角形组合而成,利用面积公式列出代数关系式:化简后就是a2+b2= c2.
5年后,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他这种直观、简捷、易懂的证明方法,就把这一证法称为勾股定理的“总统证法”,这在数学史上传为佳话.
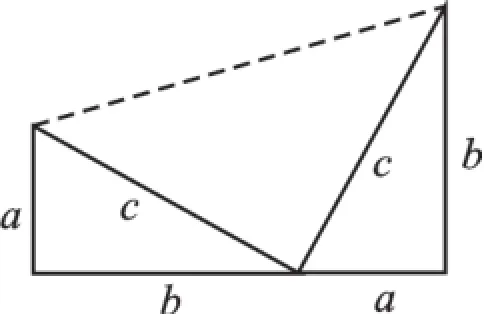
图4
法4——欧几里得法
图5是欧几里得编纂的《几何原本》中证明勾股定理的方法,四边形ABFE、AJKC、BCIH分别是以Rt△ABC的三边为一边的正方形.过C点作AB的垂线,交AB于点D,交FE于点G,连接HA、CF.通过证明△ABH≌△FBC(SAS),可得△ABH与△FBC等面积,而正方形BCIH的面积=BH·HI=2△ABH的面积,矩形BFGD的面积=BF·FG=2△FBC的面积,得到正方形BCIH与矩形BFGD等面积,同理正方形AJKC与矩形DGEA也等面积,所以正方形ABFE的面积=矩形BFGD的面积+矩形DGEA的面积,即正方形ABFE的面积=正方形BCIH的面积+正方形AJKC的面积,于是推得AB2=AC2+BC2,也就是a2+ b2=c2.证明严谨,反映了勾股定理的几何意义.
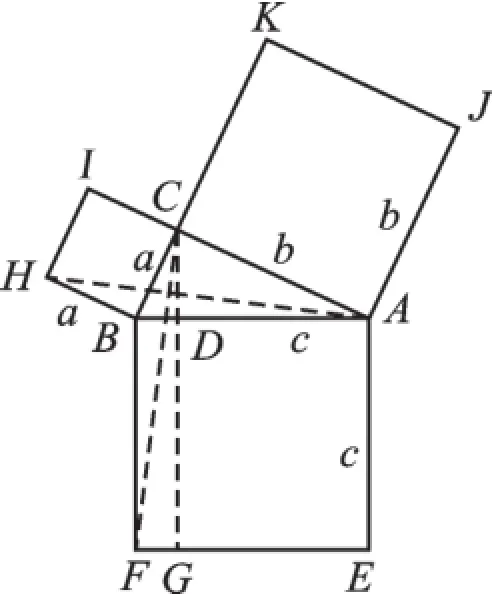
图5
证明中的剖分法、割补法、拼拆法等蕴涵着进与退、分与合、动与静、变与不变、数与形、正向与逆向、直接与间接的辩证思想方法,不仅能加深我们对勾股定理的认识,而且能引导大家感悟中西方数学家不同的思维特点.从文化的角度对各种证法作比较和欣赏.这些方法不仅验证了勾股定理,而且丰富了人们研究数学问题的方法和策略,促进了数学的发展.
2002年国际数学家大会在北京召开,为弘扬我国古代数学文明,大会选用了“弦图”作为会标的中心图案,如图6.

图6
徐利治先生认为:“数学美包括数学概念的简单性、统一性,结构系统的协调性、对称性,数学命题和数学模型的概括性、典型性和普通性,还有数学的奇异性.”勾股定理中蕴涵着丰富的数学美,在学习中同学们要善于发现美、欣赏美,并在美的指引下不断去探索与发现,这也是数学文化教育的一种体现.
勾股定理的图形很美.“弦图”简洁大方,像一只转动的风车,体现了图形的对称美.1995年,希腊专门为纪念毕达哥拉斯定理发行了一枚纪念邮票(图7),充分展现了数学图形和公式美的统一,将这一图案不断地延续下去,得到动态美丽的“勾股树”(图8),如数学文化的生命之树,生生不息.
数理哲学家罗素说:“数学如果正确看待它,不但拥有真理,而且具有至高的美.”数学家华罗庚认为勾股定理可以作为人类探寻“外星人”、与“外星人”沟通的语言,因为勾股定理的图形语言是客观存在的(图9).

图7
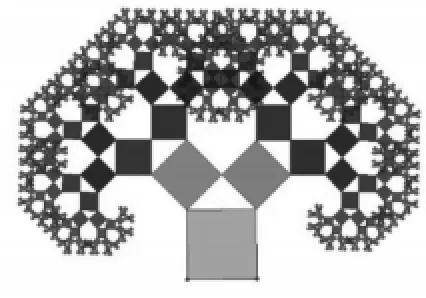
图8

图9
数学文化教育在传播数学知识的同时,还传播数学思想、方法、精神和文化,培养同学们求真、求善、求美、创新、探索的精神.揭示数学文化中所蕴涵的哲学、美学、文学和语言学等文化基因,使大家能受到良好的文化熏陶.
(作者单位:江苏省武进区礼河实验学校)
责任编辑:沈红艳见习编辑:李诗
——造梦城市中的精神绿洲

