图形折叠有玄机勾股定理来探秘

王丽花

图形折叠有玄机勾股定理来探秘

王丽花

email：czsshy@126.com

勾股定理是每年中考必考的重要知识点，以填空题、选择题、解答题等多种方式呈现.考题往往以勾股定理为解题的基本思路，以直角三角形为基本图形.下面，我们以一道中考题的变式拓展为例来一起探究勾股定理的奥秘吧！

一、原题呈现

（2015·江苏泰州中考题）如图所示，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD，则AP的长为.

【解析】设BE与CD相交于点F，AP的长为x，则由折叠可知PE=AP=x，DP=6-x，观察图形，根据“ASA”判定方法易证△DPO≌△EFO，所以PO=FO，EF=DP=6-x，所以DF=PE=x，BF=BE-EF=2+x，CF=DC-DF=8-x，在Rt△BCF中，BF2=BC2+CF2,即（2+x）2=36+(8-x)2,求得x=.故AP的长为

【点评】本题主要考查的是勾股定理及三角形全等的知识.在一个直角三角形中，已知两边可以直接求出第三边.若直角三角形中只有一边是已知的量，另外两边可以通过探究线段之间的数量关系来求，然后由勾股定理列出方程求解未知数.

二、拓展探究

拓展1以直角三角形为基本图形的几种折叠.

（1）如图1，在Rt△ABC中，∠B=90°，AB=3，BC=4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，求EB的长.

图1

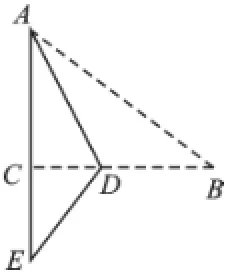
图2

图3

【解析】在Rt△ABC中，AB2+BC2=AC2，所以AC=5，由折叠可知AB′=AB=3，B′E=BE，则B′C =2，设BE=x，则B′E=x，EC=4-x，在Rt△B′EC中，B′E2+B′C2=EC2，即（4-x）2=4+x2,求得故EB的长为

（2）如图2所示，有一张直角三角形纸片ABC，∠C=90°，AC=3cm，BC=4cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为（）

A.1cmB.1.5cmC.2cmD.3cm

【解析】在R t△ABC中，AC2+BC2=AB2，所以AB=5，由折叠可知AE=AB=5，则CE=AE-AC=2.

（3）如图3所示，已知Rt△ABC中，∠C= 90°，AC=9，BC=12，将它的锐角A翻折，使点A落在边BC的中点D处，折痕交AC边于点E，交AB边于点F，则DE的长为.

【解析】在Rt△ABC中，AC2+BC2=AB2，所以AB=15，因为点D是BC的中点，所以CD=BD= 6，设AE=x，由折叠可知AE=ED=x，所以EC= 9-x，在R t△ECD中，EC2+CD2=ED2，即x2=36+ (9-x)2,求得x=

【点评】以上三个题目都是以直角三角形为基本图形进行的不同折叠，根据折叠部分全等的特征，可以得到对应线段相等.这类题目可以归为同一类，通过折叠得到线段的等量关系，选择合适的直角三角形，通常结合勾股定理和方程思想就能求解.

拓展2以矩形为基本图形的折叠.

如图4，在矩形ABCD中，AB=3，BC=4，点E是BC边上的一点，连接AE，把∠B沿AE折叠，使点B落在点F处.当△CEF为直角三角形时，BE的长为.

图4

【解析】①若∠EFC=90°，则由折叠可知∠AFE=∠ABE=90°,所以∠EFC+∠AFE=180°，所以点A、F、C在同一条直线上，AF=AB=3，在Rt△ABC中，AB2+BC2=AC2，所以AC=5，所以FC=2，在Rt△EFC中，设BE=x，EF2+FC2=EC2，即（4-x）2=4+x2,所以可求得此时BE的长为②若∠FEC=90°，则∠FEB=90°，则由折叠可知∠AEB=∠AEF=45°,所以Rt△ABE是等腰直角三角形，所以BE=AB=3.此时BE的长为3.③若∠FCE=90°，则点F落在CD边上，此时AF＞AD,不符题意，舍去.故BE的长为或3.

【点评】本题要对Rt△EFC进行分类讨论，其中有两类是符合题意的，第三类不符题意舍去.分类讨论的依据是直角顶点不同，分类讨论时要注意不重不漏.

拓展3平面直角坐标系中函数图象的折叠.

如图5，在平面直角坐标系中，O为坐标原点，一次函数y=-x+4的图象与x轴、y轴分别

交于A、B两点，若将平面直角坐标系沿∠BAO的平分线翻折，使点B落在x轴上的点C处，求折痕与y轴的交点D的坐标.

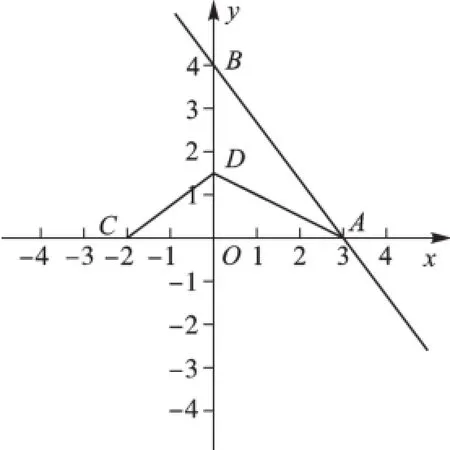
图5

【点评】本题考查了一次函数及其应用，表面上看是平面直角坐标系的折叠，归根到底仍然可以看作是直角三角形的折叠问题.

（作者单位：江苏省常州市前黄初级中学）

责任编辑：沈红艳见习编辑：李诗