“勾股定理”之我见

常州市武进区遥观初级中学八（4）班　张　健

“勾股定理”之我见

常州市武进区遥观初级中学八（4）班张健

email：czsshy@126.com

上课时，老师讲了多种关于“勾股定理”应用的数学思想，我听了之后，很是受用.在解题过程中，我又发现，除了老师讲的知识外，在《勾股定理》这一章中，还渗透着化归的思想.下面我就以学习过程中遇到的题目为例，跟大家分享一下我的发现吧！

一、化归

原题：如图4-1，有一圆柱体，它的高为16cm，底面半径为4cm，在圆柱的下底面点A处有一个蜘蛛，它想吃到上底面上与点A相对的点B处的苍蝇，需要爬行的最短路径是多少cm（π取3）？

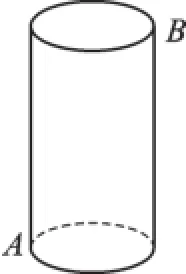
图1

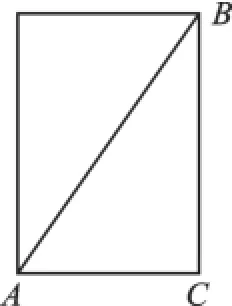
图2

蜘蛛在圆柱侧面上爬行，所以这道题是求几何体表面的最短距离，这就需要把圆柱的侧面展开.这样就把问题转化成了平面上两点间距离最短的问题，即化“曲面”为“平面”.如图2，把圆柱的侧面展开，即为长方形，根据“两点之间线段最短”可知，线段AB的长即为蜘蛛爬行的最短路径.其中BC的长等于圆柱的高16cm，AC的长等于圆柱底面周长的一半12cm.由勾股定理，在Rt△ABC中得，AB2=AC2+BC2，则AB=20.

由于这道题用到了刚学习的勾股定理，所以我印象深刻，化归思想也印在了我的脑海里，不久后，我发现，这样类型的题还真不少.

同类题型：如图3，有一个长方体纸箱，长是60cm，宽和高都是40cm.一只蚂蚁从顶点A沿纸箱表面爬到顶点B，它所爬行的最短路线的长是多少cm？

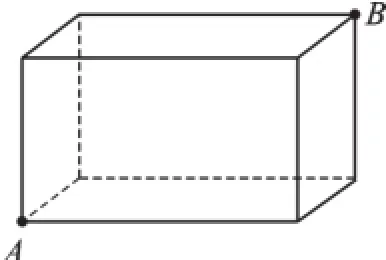
图3

这道题中除了化归的思想方法外，还要运用分类讨论的思想方法.把纸箱六个面分别记为“前、后、左、右、上、下”，则蚂蚁爬行的路线可分四种：“前”+“上”，“前”+“右”，“左”+“上”，“左”+“后”.看来只要我留心一点，这类题目对我来说就有规可循了！

数学知识奇妙无比，如果我们学习时注意归纳反思，那么一定能使自己的学习更上一层楼！

（指导教师：戚静宇）

责任编辑：沈红艳见习编辑：李诗