铁路集装箱吊装动力学分析与仿真

李可佳

LI Ke-jia

（中国铁道科学研究院 运输及经济研究所，北京 100081）

(Transportation and Economics Research Institute， China Academy of Railway Sciences， Beijing 100081， China)

铁路集装箱吊装动力学分析与仿真

李可佳

LI Ke-jia

（中国铁道科学研究院 运输及经济研究所，北京 100081）

(Transportation and Economics Research Institute， China Academy of Railway Sciences， Beijing 100081， China)

铁路集装箱在吊装过程中产生的摇摆会降低集装箱的装卸效率，为了降低集装箱在装卸过程中的摇摆程度，提高集装箱装卸效率，利用拉格朗日方程建立集装箱吊装系统的动力学模型，分析不同因素对集装箱摆动角的影响，找出导致箱体摇摆的主要原因，利用 ADAMS 仿真环境对没有防摇和采用交叉绳防摇 2 种方案的集装箱摇摆情况进行比较分析。

集装箱吊具；动力学模型；防摇

近年来，我国铁路集装箱运输的快速发展对集装箱的装卸效率提出了更高的要求，而集装箱的装卸效率主要取决于集装箱在吊装过程中的摇摆程度。为降低集装箱在装卸过程中的摇摆程度，我国铁路货场和集装箱办理站都对集装箱吊具提出了防摇要求，目前主要采用机械式防摇方案，如交叉绳防摇、倒八字绳系防摇等[1-3]。在集装箱吊装搬运期间，起重机的大 (小) 车加速度、起吊钢丝绳的长度、集装箱的升降速度等不同因素对箱体的摇摆会起到不同程度的作用。为了对现有的防摇方案进行改进和优化，有效抑制箱体的摆动幅度，分析各因素对集装箱搬运过程中摇摆程度的影响，建立集装箱吊装系统动力学模型。

1　集装箱吊装系统描述及动力学建模

集装箱吊装系统由起重机小车、起吊钢丝绳和箱体 3 部分组成。假设箱体的质心为 Oc，箱体上表面中心为 P，起吊钢丝绳一端与箱体上表面中心P 点相接，另一端与起重机小车上 Po点相接，在 Oc点建立系统坐标系 OcXcYcZc，P 点建立系统坐标系OPXPYPZP，Po建立系统坐标系 OXYZ，在任意点建立惯性坐标系 OwXwYwZw，如图1 所示。

图1 集装箱吊装系统

设在惯性坐标系中 Po点的坐标为 (xpo，ypo，zpo)，P 点的坐标为 (xp，yp，zp)，则 P 点与 Po点的位置关系可表示为式中：Lr为钢丝绳的长度，m；θx和 θy分别为钢丝绳与 YOZ 平面和 XOZ 平面的夹角，°。

将公式 ⑴ 对时间 t 求导得到点 P 在惯性坐标系中的速度为

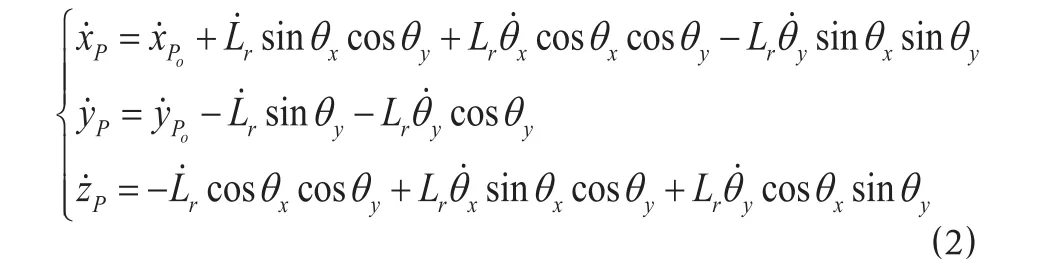
在吊运集装箱过程中箱体除了平动外还会出现转动，由于箱体的质心不在 P 点，根据平行轴定理得到箱体绕坐标轴 XP，YP，ZP的转动惯量为

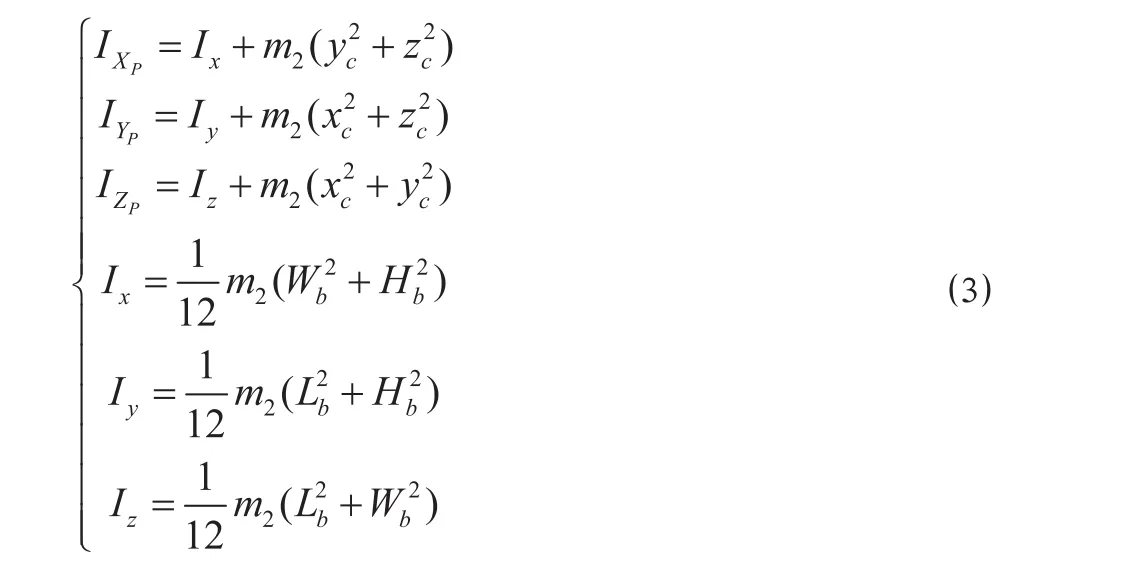
式中：IXP，IYP，IZP分别为箱体绕 XP，YP，ZP坐标轴的转动惯量，kg · m2；Ix，Iy，Iz分别为箱体绕 Xc，Yc，Zc坐标轴的转动惯量，kg · m2；xc，yc，zc分别为集装箱质心 Oc相对于箱体上表面中心 P 在 Xc，Yc，Zc轴上的偏置量，m；Lb，Wb，Hb分别为箱体的长宽高，m；m2为集装箱的质量，kg。

钢丝绳重量忽略不计[4]，集装箱吊装系统的动能为小车的动能和集装箱的动能之和 T 可表示为

式中：m1为小车的质量，kg；ax，ay，az分别为集装箱绕 P 点坐标轴 XP，YP，ZP的转角，°。

集装箱的势能 P 为

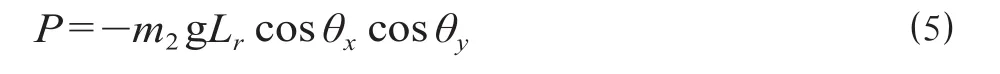
集装箱吊装系统的广义坐标 qi(i = 1，2，…，8) 为 (xpo，ypo，Lr，θx，θy，ax，ay，az)，根据拉格朗日方程[5-6]

式中：L 为拉格朗日函数 L = T-P；Fqi为 qi所对应的广义力。

整理得到集装箱摇摆的动力学模型为

从模型 ⑺ 可以发现，集装箱的摆动角 θx，θy与小车加速度、大车加速度、钢丝绳长度 Lr、升降速度及集装箱的质量 m2相关。其中，只对 θx起作用，只对起作用，其余因素对 θx和θy均有作用。

2　集装箱摇摆因素分析

为了分析大 (小) 车的加速度、绳长、升降速度等参数对集装箱摇摆偏角的影响程度，利用MATLAB 软件对方程组进行编程计算和仿真。虽然集装箱的摆动是小车和大车合成运动导致的，但分析或对箱体摆动的影响时可以单独进行，只需将另外一个方向的摆动速度或设定为 0。

假设初始条件为小车加速度 a = 2m/s2，绳长Lr= 5 m，绳的升降速度为= 2m/s2。由于集装箱的摆动角很小，可以对其进行线性化处理，即 sin θx≈ θx，sin θy≈ θy，cos θx≈ 1，cos θy≈ 1。不同参数变化对 θx和 θy的影响分别如图2、图3 所示。初始条件下集装箱在 X 轴和 Y 轴 2 个方向上的摆角变化情况如图2、图3 中的黑色实线所示，摆动角 θx的变化范围在 ±12°附近，摆动角 θy的变化范围在 ±3°附近。当小车加速度或大车加速度提升 50% 且其余条件的值不变时，θx和 θy的变化情况如图2、图3 中的红色虚线所示，大 (小) 车的加速度变化对于箱体摆角的影响明显，θx和 θy的变化周期都没有变化，但摆角的变化范围分别由 ±12°和±3°增加到 ±23°和 ±6°，摆角的变化幅度较大。当钢丝绳的上升速度提升 50% 且其余条件的值不变时，θx和 θy的变化情况如图2、图3 中的蓝色点划线所示，钢丝绳上升速度对 θx和 θy2 种摆角的影响较小，蓝色点划线和黑色实线几乎重合。当钢丝绳的长度增加 50%且其余条件的值不变时，θx和 θy的变化情况如图2、图3 中的紫色虚线所示，钢丝绳长度的增加对摆角幅度的影响较小，但钢丝绳变长导致摆角变化的反应速度下降，紫色虚线的变化周期比黑色实线长。这表明，大 (小) 车的加速度对集装箱摆角幅度影响大；钢丝绳的升降速度变化对集装箱摆动的影响较小；钢丝绳长度变化对于摆角的幅度影响不大，但对摆角的变化周期有影响，钢丝绳越长集装箱的摆动周期越长。

图2 不同参数变化对θx 的影响

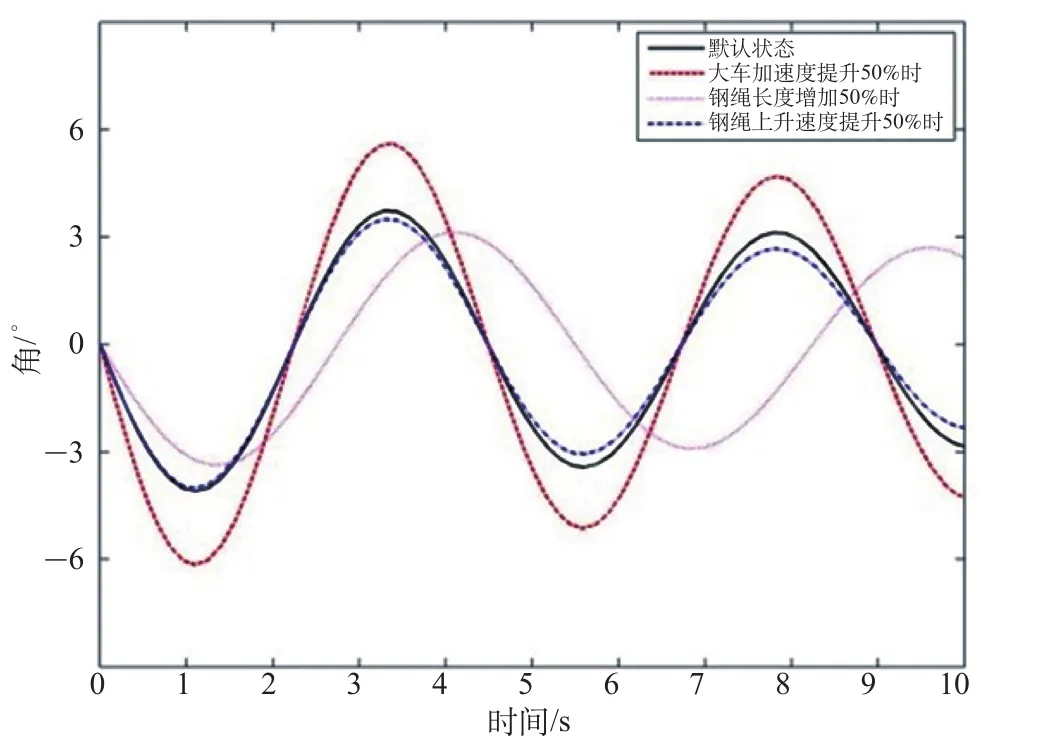
图3 不同参数变化对 θy的影响

3　集装箱吊装仿真分析

交叉绳防摇是我国铁路集装箱专用吊具常采用的防摇措施之一，为了揭示该措施的防摇效果，在随机给定加速度变化的条件下，对集装箱没有防摇方案和采用交叉绳防摇方案的摆动情况进行对比分析。利用 ADAMS 动力学仿真环境建立模型[7-8]，如图4 所示。

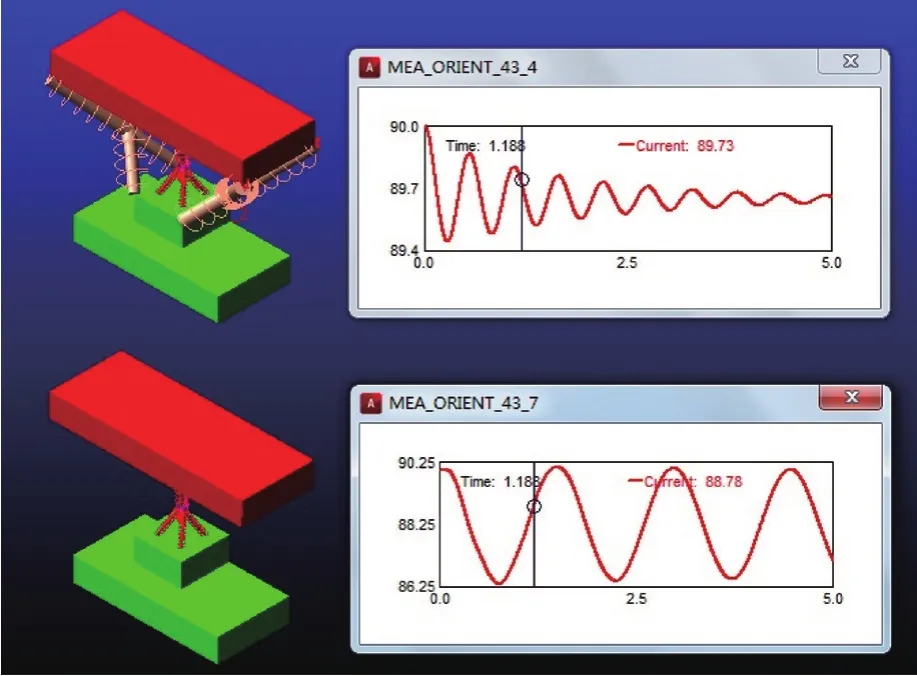
图4 集装箱吊运仿真模型

图4 中红色长方体为起重机上的小车，绿色的2 层模块为集装箱吊具的上架体和下架体，小车与吊具之间的红色绳为起吊绳，粉色绳为防摇绳，各绳均利用弹簧单元模拟。仿真初始时刻，小车和吊具的速度为 0，起吊绳与 X 轴方向的夹角为 90°。小车加速度在起初的 3 s 内由 0 m/s2迅速增加到1.5 m/s2，随后加速度数值持续下降，在第 7 秒时达到最小值 -1 m/s2，之后又开始上升，在最后时刻变为 1 m/s2，仿真时间为 10 s。小车加速度随机变化情况如图5 所示。

图5 小车加速度随机变化图

小车加速度随机变化情况下吊具夹角变化没有防摇和采用交叉绳防摇 2 种方案的仿真结果如图6 所示。图6 中红色实线为没有防摇绳条件下起吊绳与 X 轴方向夹角的变化情况，蓝色虚线为有交叉防摇绳作用下夹角的变化情况。在没有防摇绳情况下，夹角的变化范围在 77.5°～102.5°之间，仿真期间共出现 4 次波峰、5 次波谷，并且没有减小趋势，集装箱的摇摆频次多、幅度大；在采用交叉防摇绳作用下，夹角的变化范围控制在 87.5°～92.5°之间，夹角变化幅度小且曲线平滑，集装箱摇摆轻缓，可见采用交叉绳防摇的效果十分明显。

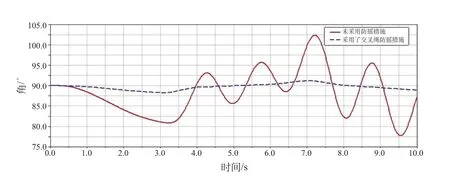
图6 小车加速度随机变化情况下吊具夹角变化图

4　结束语

为提高铁路集装箱的装卸效率，需要采用有效的防摇措施，抑制集装箱体的摆动幅度，在最短时间内将集装箱摆角控制在最小范围。建立并应用集装箱吊装系统动力学模型，分析不同因素对集装箱摇摆的影响程度，找出导致集装箱摇摆的主要原因，为实现对现有的防摇方案进行改进和优化提供理论依据。利用 ADAMS 动力学仿真环境，直观比较分析防摇方案的效果，为评价和创新防摇方案提供理论支撑。

[1] 邹 胜. 集装箱起重机吊具止摆装置的工作原理及计算[J].起重运输机械，1994(7)：3-6. ZOU Sheng. Operation Principle and Calculation of Spreader Anti-sway Device Used for Container Crane[J]. Hoisting and Conveying Machinery，1994(7)：3-6.

[2] 金晓春，李映新，张 寒，等. 集装箱吊具智能防摇装置性能分析[J]. 铁道货运，2013，31(11)：47-52. JIN Xiao-chun，LI Ying-xin，ZHANG Han，et al. Analysis on Performance of Intelligent Anti-sway Device in Container Lifting Appliances[J]. Railway Freight Transport，2013，31(11)：47-52.

[3] 李维越. 起重机常用防摇系统分析[J]. 起重运输机械，2007(9)：51-53. LI Wei-yue. Anti-swing Systems Commonly Used in Cranes [J]. Hoisting and Conveying Machinery，2007(9)：51-53.

[4] 程文明，钟 斌，张则强，等. 集装箱起重机液压油缸式减摇系统的动力学分析[J]. 中国铁道科学，2008(2)：105-109. CHENG Wen-ming，ZHONG Bin，ZHANG Ze-qiang，et al. Dynamic Analysis for the Structure of the Container Crane Hydraulic Anti-sway System[J]. China Railway Science，2008(2)：105-109.

[5] LI Ke-jia，DING Xi-lun， Ceccarelli M. A Total Torque Index for Dynamic Performance Evaluation of a Radial Symmetric Six-legged Robot[J]. Frontiers of Mechanical Engineering，2012，7(2)：219-230.

[6] Oguaman D C D，Hansen J S. Dynamics of a Threedimensional Overhead Crane System[J]. Journal of Sound and Vibration，2001，242(3)：411-426.

[7] McConville J B，McGrath J F. Introduction to ADAMS Theory[R]. Michigan：Mechanical Dynamics Inc，1997.

[8] 李 军，邢俊文，覃文浩，等. ADAMS 实例教程[M]. 北京：北京理工大学出版社，2002.

责任编辑：王 静

Dynamic Analysis and Simulation of Railway Container Lifting

The swing occurred in lifting process of railway container will reduce loading efficiency of container. In order to reduce the swing degree in loading process of container and increase the loading efficiency, the dynamic model of container lifting system was established by using Lagrange method. This paper analyzes the influence of different factors on swing angle of container, points out main reasons causing the swing of box body, and by using ADAMS simulation environment, compares and analyzes the container swing status of 2 programs, which are the program of having no anti-swing and the program of applying anti-swing with cross-lay rope.

Container Spreader ; Dynamic Model; Anti-swing

1003-1421(2016)05-0080-04

U294.3

B

10.16668/j.cnki.issn.1003-1421.2016.05.17

2016-03-14

中国铁道科学研究院科研项目 (2011YJ75)