铁路行包运输运能分配方案研究

母柏松，王 莹，李慧玲

MU Bai-song1, WANG Ying1, LI Hui-ling2

（1.北京交通大学交通运输学院，北京100044；2.南昌铁路局客货运输统计所，江西南昌330000）

(1.School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China; 2.Passenger and Freight Transport Statistics Institute, Nanchang Railway Administration, Nanchang 330000, Jiangxi, China)

铁路行包运输运能分配方案研究

母柏松1，王 莹1，李慧玲2

MU Bai-song1, WANG Ying1, LI Hui-ling2

（1.北京交通大学交通运输学院，北京100044；2.南昌铁路局客货运输统计所，江西南昌330000）

(1.School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China; 2.Passenger and Freight Transport Statistics Institute, Nanchang Railway Administration, Nanchang 330000, Jiangxi, China)

铁路行包货物具有批量小、到站分散、种类繁多的特点。在实际运输过程中，由于行包到达的不均衡和运输组织的复杂性，往往不能保证行包在车站的集中到发。对于行包作业量小的车站，很容易导致人力资源的浪费，带来运营管理成本的增加。针对这样的情况，以作业量小的车站行包尽可能集中到发为优化目标，建立了行包运输方案的线性混合整数规划模型。实例计算表明，通过该模型的求解，可以保证优先把运能分配给行包办理量小的车站，从而达到降低铁路运营管理成本的目的。

铁路；行包运输；运能分配；混合整数规划

铁路行包运输是使用旅客列车编挂的行李车运输的一种小件物资快运形式[1]，它具有通达范围广、运输速度快、准时性较好的优点，但由于运能较小，其运输的货物具有批量小、到站分散、种类繁多的特点，运输组织工作也较为复杂，作业环节多，需要较多的劳力、设备和机具，运输成本也较高[2]。在实际运输过程中，行包作业往往分布在全天各个时段，这就需要 24 小时配备工作人员进行行包的装卸作业。对于一些行包装卸量小的车站，势必会造成人力资源的浪费，带来运营管理成本的增加[3-4]。研究行包运输的运能分配方案问题，在确保所有商品能够到达目的地的同时，使作业量小的车站行包尽可能集中到发，优先把运能分配给到发量小的车站，对于提高行包运输效率、降低运营成本具有重要意义[5-6]。

1　铁路行包运输运能分配模型构建

行包运输问题的目的主要是确定各起讫点行包流的运送路径，以满足小批量的行包运输需求，提高既有运输资源的使用效率[7-8]，目标是使作业量较小车站的行包可以在某一时间段集中装卸，根据这一目标构建行包运能分配的线性混合整数规划模型。

1.1 相关符号定义

S 为行包办理站的集合；S1为行包办理量较小的车站集合；Sk为列车 k 经过的行包办理站集合；T 为所有运送行包的列车集合；ai为车站 i 开始办理行包业务的最早时刻； bi为车站 i 结束行包业务办理的最晚时刻；为列车 k 经过车站 i 的时刻 (由于列车在中间站停站时间通常较短，取列车到达车站 i 的时刻作为计算时刻，如果 i 为始发站则取列车发车时刻)； δ 为列车 k 途经的任一中间站 (行包办理站)为 0-1 变量，由车站 i 发往车站 j 的行包由列车 k 运输时为 1，否则为 0；为由列车 k 运输的车站 i 发往车站 j 的行包运量；Dij为由车站 i 发往车站 j 的行包运输需求量；μk为列车 k 的行李车载重能力；为列车 k 经过车站 i 的顺序 ( i = 0，1，2，…)，在研究范围内经由的第一个车站取值为1，其余顺次排序，如果不经过则取值为 0；Ti为经过车站 i 的列车集合；M 为一个足够大的整数，用于将非线性约束转为线性约束。

1.2 模型构建

构建行包运能分配目标函数，使行包办理量较小的行包办理站的总作业时间最短。

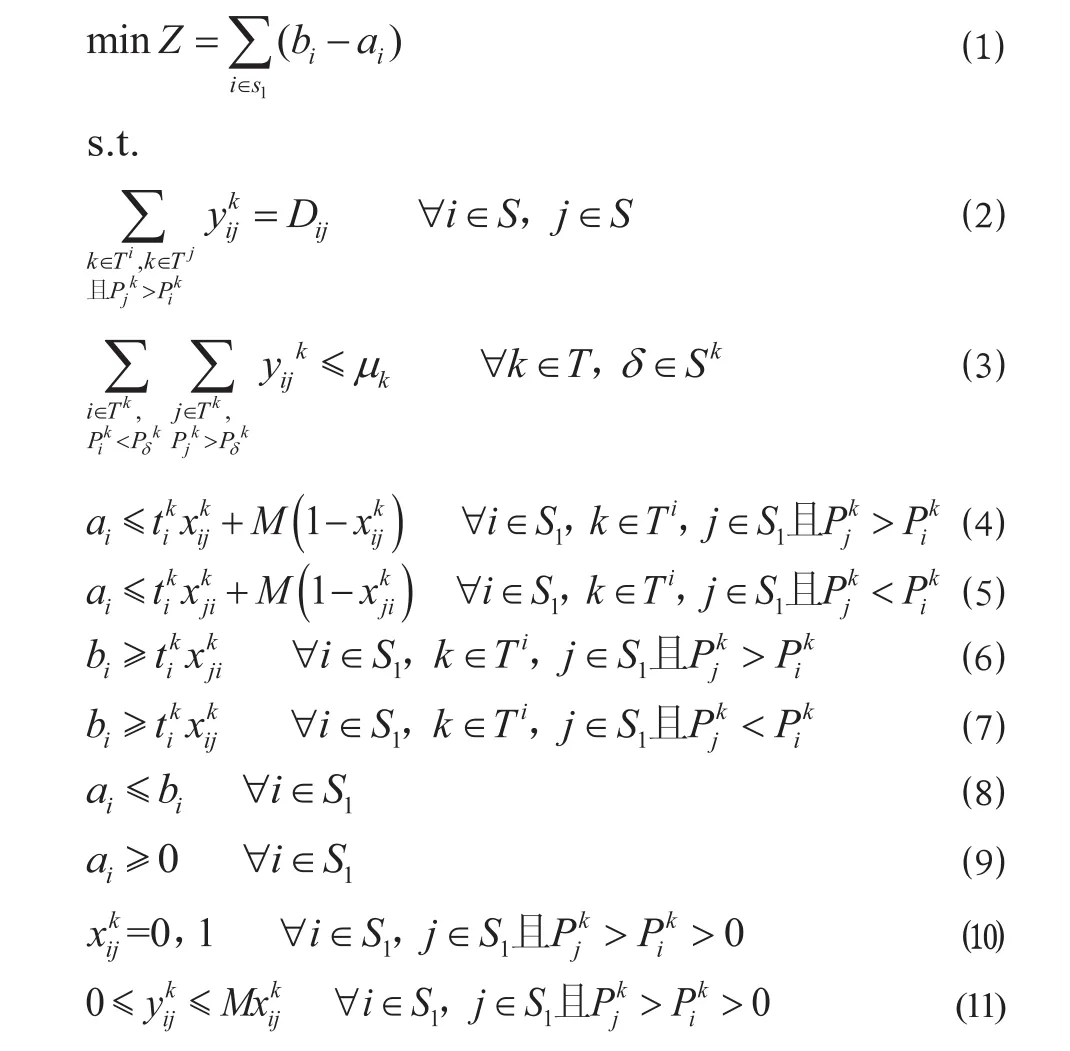
⑵ 式为 O-D 流量约束，表示从车站 i 到车站 j 的行包运量总和等于车站 i 到车站 j 的行包运输需求量；⑶ 式为能力约束，对于列车 k 经过的任意一站 δ，其前行车站 i 至后行车站 j 的累计装载量小于等于行李车的载重能力 μk；⑷ 式表示 ai的值不大于任何一件行包从 i 站发出的时刻；⑸ 式表示 ai的值不大于任何一件行包到达 i 站的时刻，从而保证 ai的取值为 i 站最早办理行包作业的时间；与 ai的取值约束类似，⑹ 式与 ⑺ 式表示 bi的取值约束，使得 bi的取值为 i 站最晚办理行包作业的时间；⑻ 式与 ⑼ 式为 ai，bi的取值约束，保证 ai， bi均不小于 0 且 bi- ai的值非负；⑽ 式表示为 0-1变量，由车站 i 发往车站 j 的行包由列车 k 运输时为1，否则为 0；(11) 式表示决策变量 xkij与行包运送量的取值约束。

2　实例验证与分析

行包运能分配模型为线性混合整数规划模型，可以直接采用数学软件求解。为验证模型的可行性，以某铁路局数据为例进行行包运能分配问题的求解。该铁路局共有行包办理站 28 个，按顺序分别编号为 1—28，选取行包日均办理量小于 1.5 t的 5、7、8、11、13、15、17 这 7 个车站作为优化对象；办理行包业务的旅客列车 232 列；μk取行李车的载重量 25 t。

使用 LINGO 软件求解该线性混合整数规划模型，得出部分行包运输方案如表1 所示。

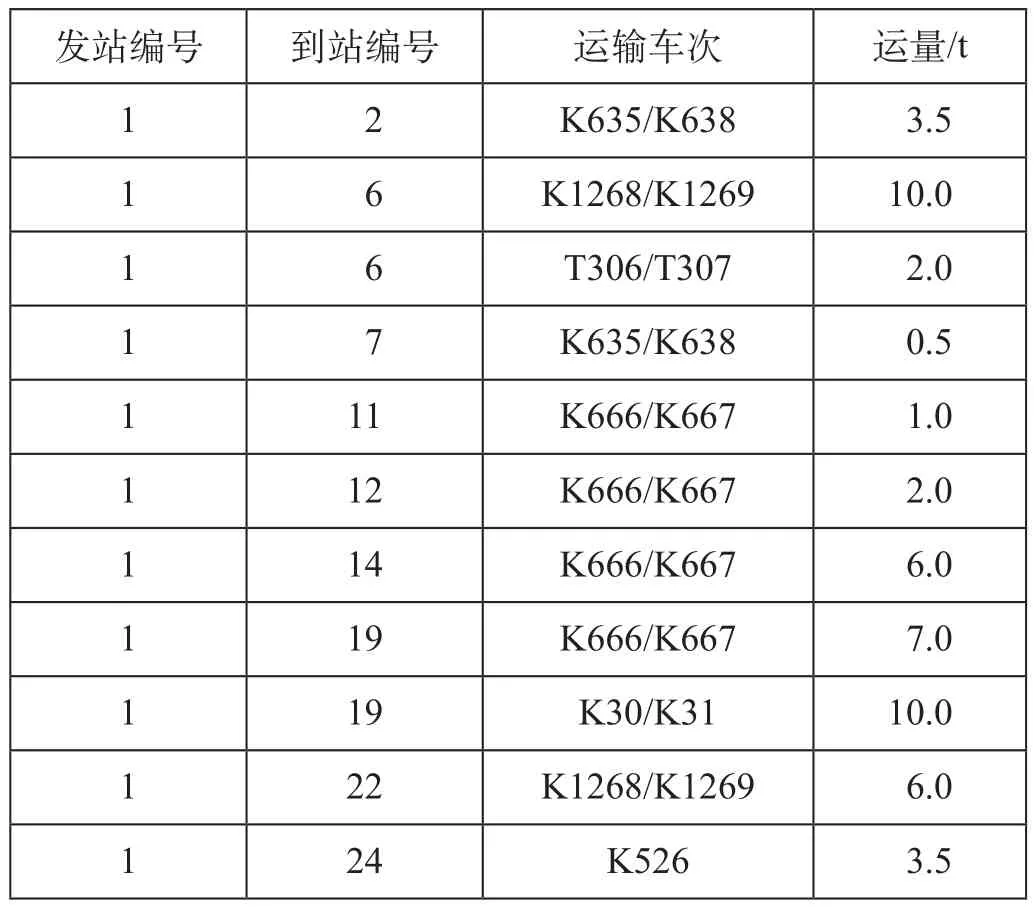
表1　 行包运输方案 (部分)

行包作业量相对较小的 7 个车站办理行包作业的时间分布情况如表2所示。7 个车站的行包作业时间均集中在 4 h 以内，其中最长 4 h，最短在1h以内，只需要配备一班作业人员即可，可减少 2/3的作业人员，大大降低人力资源成本。

3　结束语

铁路行包运输具有安全、快捷、方便等优点，适合于零散物资的快速运输。由于行包办理站较多，部分行包办理站存在着办理量小、行包作业时间分散等问题，导致较高的运营成本。通过行包运输运能分配模型能够优先把运能分配给行包办理量较小的车站，尽可能集中这些车站的行包装卸作业，从而减少车站配备的作业人员数量，达到降低铁路运营成本的目的。模型主要考虑作业量小的车站行包作业尽可能集中，在实际应用时可以根据需要进一步加入广义费用最小等优化目标，从而更加全面、客观地反映行包运营实际，为铁路行包运输提供决策参考。

表2　 作业量较小的车站办理行包作业的时间分布情况

[1] 沈 睿. 铁路行包快运服务网络设计理论与方法研究[D].北京：北京交通大学，2006.

[2] 黄 鉴，彭其渊. 基于时刻表的客运专线列车客流分配研究[J]. 铁道运输与经济，2012，34(11)：40-43. HUANG Jian，PENG Qi-yuan. Research on DPL Passenger Flow Distribution based on Timetable[J]. Railway Transport and Economy. 2012，34(11)：40-43.

[3] 李先进. 铁路行包运输组织方法及其优化研究[D]. 北京交通大学，2007.

[4] 聂 磊，胡小风，佟 璐，等. 基于旅客列车开行方案的客流分配方法研究[J]. 交通运输系统工程与信息，2011，11(3)：87-92. NIE Lei，HU Xiao-feng，TONG Lu，et al. Research of Passenger Flow Assignment based on Passenger Train Plan[J]. Journal of Transportation Systems Engineering and Information，2011，11(3)：87-92.

[5] 陶思宇. 客运专线网络旅客列车开行方案优化设计与调整研究[D]. 西南交通大学，2012.

[6] 佟 璐，聂 磊，付慧伶. 基于复杂列车服务网络的客流分配方法研究[J]. 铁道学报，2012，34(10)：7-15. TONG Lu，NIE Lei，FU Hui-ling. Research on Passenger Flow Assignment Method based on Complex Train Service Network[J]. Journal of the China Railway Society，2012，34(10)：7-15.

[7] 漆 昕，熊 坚. 基于停站方案的旅客列车开行方案优化研究[J]. 铁道运输与经济，2012，34(12)：43-47. QI Xin，XIONG Jian. Research on Optimization of Passenger Train Operation Diagram based on Stopping Diagram[J]. Railway Transport and Economy，2012，34(12)：43-47.

[8] 王保华，何世伟，宋 瑞，等. 快捷货运动态服务网络设计优化模型及其算法[J]. 铁道学报，2009，31(5)：17-22. WANG Bao-hua，HE Shi-wei，SONG Rui，et al. Optimization Model and Algorithm of Dynamic Express Shipment Service Network Design[J]. Journal of the China Railway Society，2009，31(5)：17-22.

责任编辑：刘 新

Study on Distribution of Railway Luggage & Parcel Transportation Capacity

Railway luggage&parcel has the characteristics of small volume, dispersion in arrival station and diversified categories. During the actual transportation, because of unbalanced luggage&parcel arrival and departure and complex transport organization, the centralized arrival and departure of luggage & parcel in station usually cannot be ensured. For stations with small volume, their labor resource will be easily wasted, and the operational management cost will increase as a result. Targeting with above status, taking centralized luggage&parcel arrival and departure in the stations with small volume as the optimization objective, the linear mixed integer programming model of luggage&parcel transport was established. The calculation of actual example shows that luggage&parcel could arrive and depart at stations with small volume on a relatively high dgree of concentration, so as to reduce railway operational management cost.

Railway; Luggage&Parcel Transportation; Distribution of Transport Capacity; Mixed Integer Programming

1003-1421(2016)04-0027-03+3

A

U293.2

10.16668/j.cnki.issn.1003-1421.2016.04.07

2015-12-09

中国铁路总公司科技研究开发计划项目(2015F020)