动车组转向架轴承局部损伤振动特性分析

杨天蕴， 丁 千， 郭 涛， 贾尚帅

(1.天津大学力学系 天津，300072) (2.天津市非线性动力学与混沌控制重点实验室 天津，300072) (3.唐山轨道客车有限责任公司 唐山，064000)



动车组转向架轴承局部损伤振动特性分析

杨天蕴1,2， 丁 千1,2， 郭 涛3， 贾尚帅3

(1.天津大学力学系 天津，300072) (2.天津市非线性动力学与混沌控制重点实验室 天津，300072) (3.唐山轨道客车有限责任公司 唐山，064000)

针对动车组转向架轴承，根据轴承故障产生机理建立了轴承故障动力学工程模型。模型充分考虑了车轴弯曲刚度、轴承间隙及滚动体和滚道间的非线性接触力等因素，并包含内圈、外圈以及滚动体故障轴承动力学模型，使用龙格库塔数值积分方法进行了动力学仿真分析。针对实际轴承搭建实验台，对不同故障类型及不同程度故障进行了实际测试。仿真分析与实验结果吻合度较高，最大误差不超过5%，证明了该动力学模型的有效性。

转向架轴承； 故障； 动力学模型； 特征频率； 检测

引 言

动车组转向架轴承作为列车走行关键部件，是动车组中工作条件最为恶劣的部件[1]。在列车运行中，它起着承受载荷和传递载荷的作用，在高铁高速重载的运营条件下，动车组转向架轴承一旦发生故障，就会严重威胁列车安全[2]。国内外学者针对转向架轴承做了一系列研究。曹青松等[3]建立了CRH1型动车组滚动轴承-车轴耦合系统非线性动力学模型，采用数值方法分析了不同工况下该系统的动力学响应与非线性特性。聂晔[2]应用故障树分析法建立了转向架轴承故障模型。颜家森等[4]建立了高铁轴箱滚柱轴承的拟动力学分析，采用数值模拟方法计算了轴承的载荷分布。在对故障轴承的动力学建模分析方面，关贞珍等[5]建立了转子-故障滚动轴承-轴承座的非线性振动模型以及轴承外圈、内圈、滚动体局部故障非线性动力学模型，运用数值积分进行仿真分析。曹宏瑞等[6]建立了滚动轴承拟静力学模型，利用一系列近似等距的冲击脉冲描述滚动体经过损伤时产生的冲击现象。张建军等[7]建立了6自由度轴承动力学模型，引入了单元谐振器模拟出现故障后轴承元件的高频固有振动，并进行了实验验证。陈恩利等[8]和东亚斌等[9]分别对轴承外圈故障和滚动体故障建立了动力学模型，并用实际轴承进行了验证。但是，对于故障轴承的动力学建模大多数研究是针对球轴承[10]，对于转向架轴承采用的圆锥滚柱轴承的研究大部分为动态刚度[11-12]和接触载荷等[13-14]，系统地对转向架圆锥滚柱轴承各部位出现损伤时的故障动力学建模还鲜有提及。

笔者针对某型动车组进口轴承的故障问题，建立了轴承系统振动模型。对正常振动和各种故障条件下的振动进行计算，并搭建实验模型进行验证，得到了该类轴承几种典型故障的振动特点。

1 转向架滚动轴承系统动力学建模

转向架轴承内圈与车轴间为过渡配合，可以看成一体且安装在车轮的外侧，内圈的支撑刚度可以通过求解车轴悬臂梁弯曲刚度得到，而车体重量作用在轴承外圈。假设转轴质量沿轴线均匀分布，内圈质量为M，轴单位长度质量为m，长为L，弯曲刚度为EI，由材料力学推导出内圈支撑刚度为

(1)

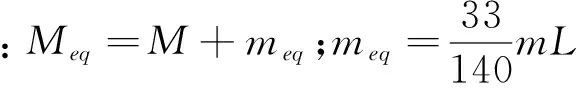
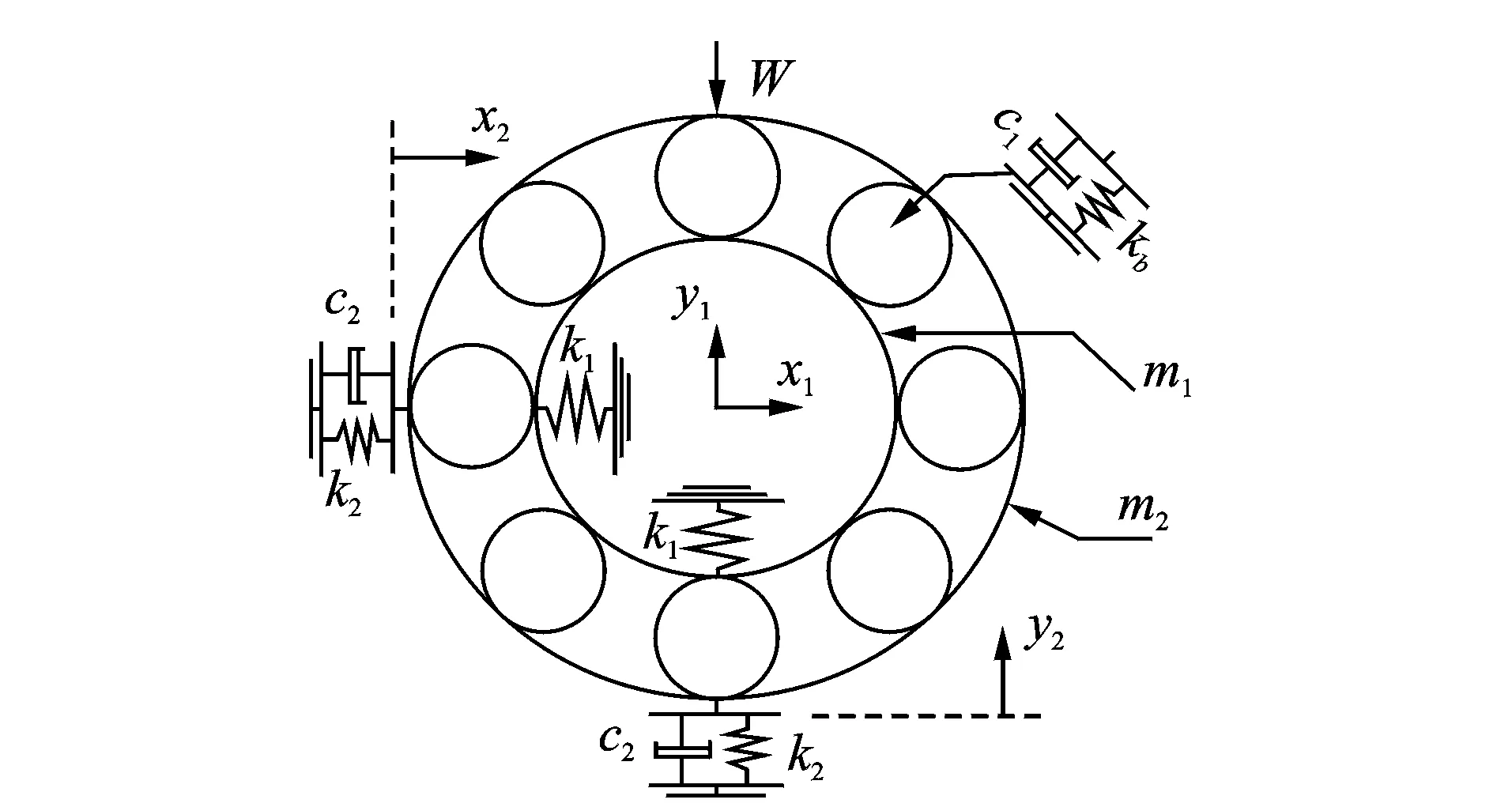
图1 正常轴承动力学模型Fig.1 The dynamic model of bearing

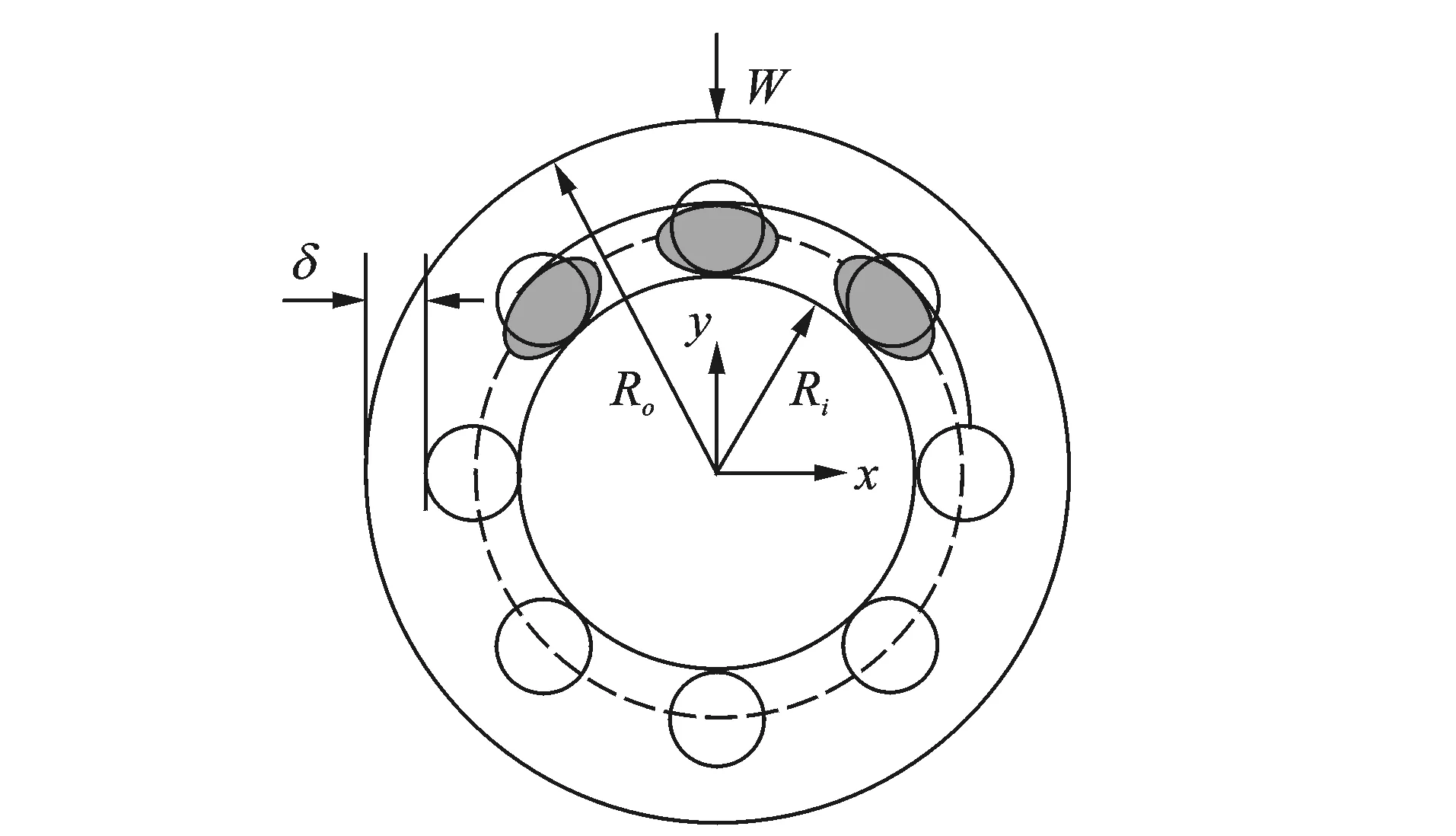
图2 变柔度振动Fig.2 The varying compliance vibration

滚动轴承的动力学模型如图1所示。研究其水平与竖直方向的振动，建立转子-轴承系统的动力学方程

其中：m1为转子和内圈质量；m2为外圈和轴承座质量；c1为轴承阻尼；kb为非线性刚度系数；c2，k2为轴承座阻尼和刚度；α为接触角；β为半锥角；Fx，Fy为轴承与内外圈水平、纵向接触力；W为车体作用在轴承外圈的压力(负荷)。

车辆运行时，转向架轴承外圈不转动，内圈转动。假定滚动体在滚道内等距排列且做纯滚动，轴承上部为承载区，外圈所受支承刚度发生周期性变化，产生变柔度振动如图2所示。设ω为转子的角速度，Ri为轴承内圈滚道半径，Ro为轴承外圈滚道半径，N为滚动体数，ωc为保持架角速度，δ为初始间隙。第j个滚动体在时间t时转动的角度为

(3)

(4)

第j个滚动体在角位置θj处的变形量为

(5)

根据赫兹接触定理，针对圆锥滚子轴承，第j个滚动体受到的接触力[15]为

(6)

其中：λj用来判断是否存在赫兹变形，当变形存在即γj>0时，λj取值为1；当不存在赫兹接触，即变形量γj<0时，λj取值为0。

在水平和竖直方向上总的接触力为

(7)

2 轴承故障模型

2.1 轴承故障特征频率

滚动轴承故障形式主要表现为内、外圈以及滚动体表面出现裂纹或剥落，这些故障均由早期的点损伤逐渐形成。当出现这些损伤时，轴承响应中都有特定的频率成分与之相对应，称为故障特征频率，理论计算公式[15]如下。

1) 外圈故障频率：N个滚动体与外圈上某一固定点接触频率

(8)

2) 内圈故障频率：N个滚动体与内圈上某一固定点接触频率

(9)

3) 滚动体故障频率：滚动体上某一固定点与外圈或内圈接触频率

(10)

其中：fs为转轴转动频率；D为轴承节径；d为滚动体直径；α为压力角。

由于转向架轴承为圆锥滚柱轴承，在滚柱的不同位置d/D是不同的。计算表明，沿着圆锥滚柱的接触应力分布相当均匀，小端的接触应力略大[13]。实际测量发现，滚柱的小、中端以及大端的d/D值分别为0.140 1，0.141 0和0.140 0，差别很小，所以笔者选滚柱的中端进行研究，取d/D的值为0.14。研究假定车厢空载重量为12t，满载重量为17t，共有4根传动轴，8套轴承支承，初始径向游隙为0.065 mm[4]。计算可知，单个轴承承受径向载荷空载时为1 500 kg，满载时为2 125 kg。

2.2 故障轴承接触力模型

2．2．1 外圈故障

假设轴承外圈出现损伤，损伤角位置为θdc且位于承载区，损伤宽度为θdt，深度为θda。当滚柱滚过损伤区域时，滚柱与外圈的间隙会增大，设变化量为δouter，间隙变化发生条件为θdc<θj<θdc+θdt，即

(11)

滚柱在损伤区的间隙变化会导致非线性赫兹接触力发生变化，变化后间隙为

(12)

2．2．2 内圈故障

假设轴承内圈出现损伤，损伤角位置为θdc，损伤宽度为θdt，深度为θda。与外圈故障不同的是，由于损伤位于内圈且内圈随转子转动，损伤角位置θdc并不固定，而是时间t的函数。设初始损伤角位置为θd0，则θdc=θd0+ωt。当滚柱滚过损伤区域时，滚柱与内圈的间隙会突然增大，设变化量为δinner，间隙变化发生的条件可表示为θdc<θj<θdc+θdt，即

(13)

内圈出现故障时间隙的变化会导致非线性赫兹接触力的变化，变化后间隙为

γj=(x1-x2)cosθj+(y1-y2)sinθj-δ-δinner

(14)

2．2．3 滚动体故障

假设轴承滚动体出现损伤，损伤角位置为θdc，损伤宽度为θdt，深度为θda。与内圈故障类似，滚动体出现损伤时角位置也是随时间变化的函数，有

(15)

其中：θd0为损伤初始角位置；ωs为滚动体自传角速度，且ωs=ωD[1-(dcosα/D)2]/2d；d为滚动体中端直径；D为轴承节圆直径；α为接触角。

滚动体在旋转一周的范围内，与内、外圈均接触一次，即损伤引起的冲击出现两次。假设第k个滚动体出现损伤，t时刻损伤角位置为θk=2π(k-1)/N+ωct。尽管滚动体自转一周与内外圈各接触一次，但损伤点与内圈接触时产生的脉冲力对外圈的作用远不及损伤点直接与外圈作用的脉冲力大[15]，因此忽略滚动体损伤与内圈接触产生的脉冲力。滚动体损伤与外圈接触条件为|mod(θdc，2π)-θdt/2-3π/2|<θdt/2，设间隙变化为δroller，则变化后的间隙为

(16)

3 轴承的振动特性动力学仿真分析

针对研究的转向架轴承，选取转轴转速为1 590 r/min，对应动车组时速为260 km/h。其他参数取值分别为Ri=82 mm，Ro=120 mm，F=21 250 N(满载时轴承承受径向载荷)，m1=30 kg，m2=35 kg，d/D=0.14，c1=7 (kN·s/m)，c2=4 (kN·s/m)，Kb=3.5×109N/m，K2=2.5×109N/m，N=17，δ=6.5×10-5m。采用龙格库塔法对轴承系统动力学方程进行数值求解。由于实际上只能测量轴承箱的振动数据，以下显示的均为外圈振动，即y2响应。

3.1 正常轴承

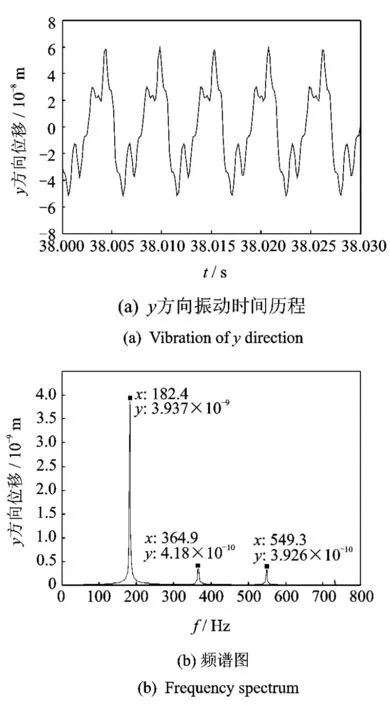
图3 正常轴承振动特性Fig.3 Vibration characteristics of bearing with no fault

对于正常轴承，自身刚度变化引起的变柔度振动频率为fv c=fsRiN/(Ri+Ro)=182.9 Hz，仿真结果如图3所示。可以看出，轴承的变刚度特性引起轴承在径向产生周期性振动，即变柔度振动，包括基频182.4，364.9和549.3 Hz等倍频。其中，基频182.4 Hz与理论计算频率fv c吻合。Fukata等[16]研究表明，当转子在远离x和y方向的临界转速时，运动是周期的，表现出滚子的转动频率及其谐波。该结论得到本研究结果的验证。

3.2 外圈故障轴承

因转向架轴承上半区为承载区，故取轴承外圈损伤角位置θdc=5.5 rad，损伤宽度θdt=0.029 rad，深度θda=1 mm。当转子转速为1 590 r/min时，计算得到轴承外圈故障频率为194.3 Hz，仿真结果如图4所示。可以看出，当滚柱经过内圈损伤时，出现明显的冲击激励。频谱图中的194.8，389.7及586.6 Hz均为外圈故障特征频率及其倍频，与理论计算结果有0.21%的误差。文献[15]指出，外圈损伤包络谱图形是一系列以外圈故障特征频率为间隔的随频率增大、幅值逐渐减小的离散谱线，本研究结果符合此结论。

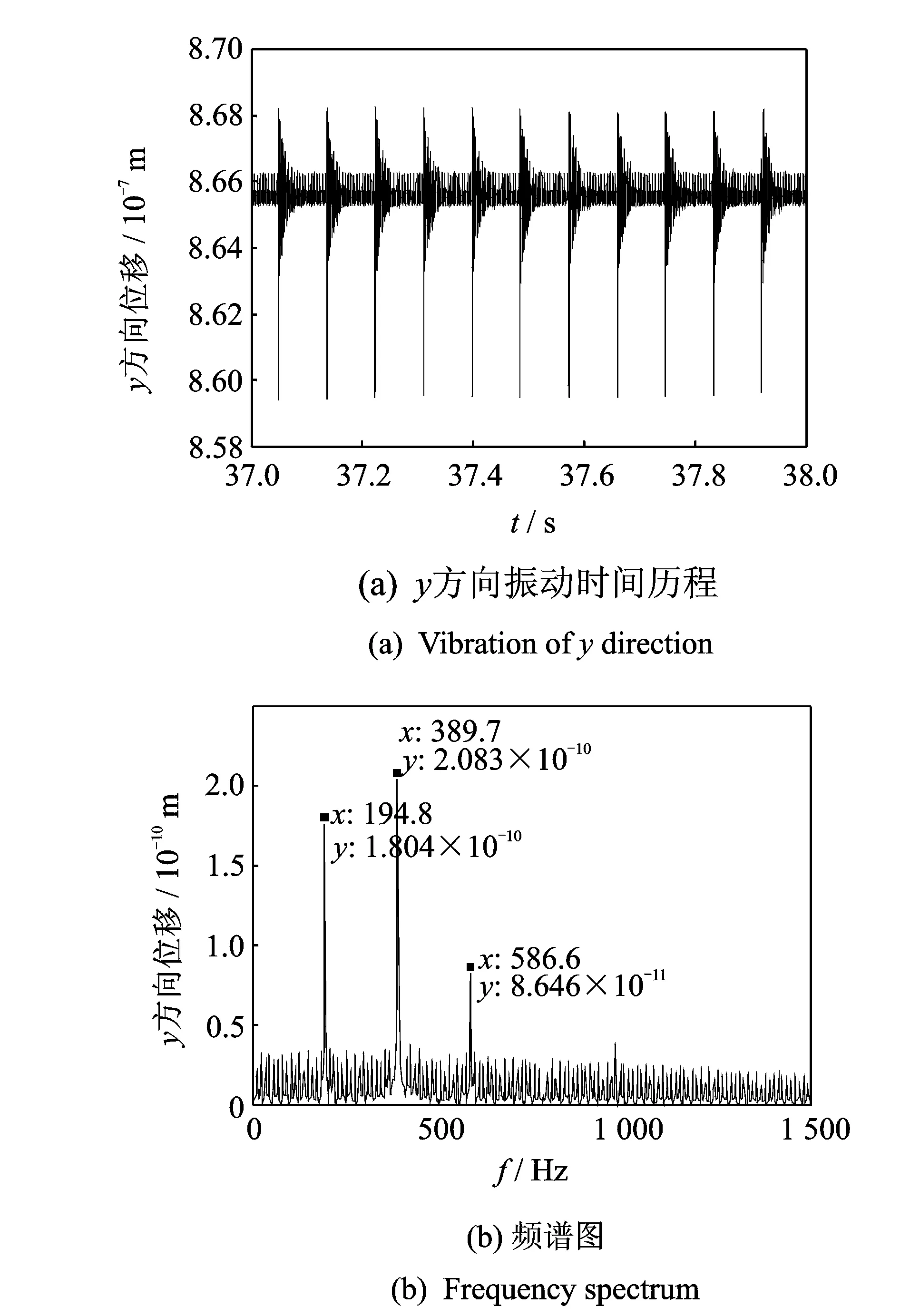
图4 外圈故障轴承振动特性Fig.4 Vibration characteristics of bearing with outer race fault

3.3 内圈故障轴承

取轴承内圈损伤初始角位置为θd0=5.5 rad，损伤宽度θdt=0.029 rad，深度θda=2 mm。当转子转速为1 590 r/min时，计算得到轴承内圈故障频率为256.2 Hz，数值求解结果如图5所示。可以看出，当滚柱经过内圈损伤时，出现明显的冲击激励，振动突然增大，然后快速衰减，如此反复。图5(b)为全频段频谱图，2 141，2 409及2 677 Hz均为内圈故障特征频率倍频，它们的差值268 Hz为内圈故障特征频率，与理论计算结果256.2 Hz仅有4.6%的相对误差。由于内圈随转子一起转动，所以内圈故障频率受到转子旋转频率的调制，在内圈故障频率的周围出现以转子旋转频率大小为间隔的边频带，在1 kHz和2.7 kHz处各出现了较大峰值。图5(c),5(d)为高频和低频共振区的局部频谱图。可见，边频带之间的间隔为26 Hz左右，等于转轴旋转频率26.5 Hz。文献[15]研究表明，内圈损伤在内圈故障特征频率的各阶倍频处有幅值逐渐下降的谱线，且以各阶倍频为中心，在两旁有间隔等于旋转频率的调制谱线。以上结果符合这一结论。

3.4 滚动体故障轴承

取轴承滚动体损伤初始角位置为θd0=0 rad，损伤宽度θdt=0.029 rad，深度θda=1 mm。当转子转速为1 590 r/min时，滚动体故障与内圈或外圈的接触频率为92.8 Hz。求解结果如图6所示。可以看出，当滚柱损伤经过内圈或外圈时，出现明显的冲击激励，振动突然增大，然后快速衰减，如此反复。图6(b)为全频段频谱图，1 578，1 671及1 764 Hz等频率值均为滚动体故障特征频率倍频，它们的差值93 Hz基本为fr。由于滚动体随轴承保持架一起转动，所以fr受到保持架旋转频率的调制，出现以保持架旋转频率大小为间隔的边频带。在600 Hz和1 600 Hz附近各出现了峰值较大区域，图6(c)，6(d)为低频和高频共振区的局部频谱图。可以观察到各个频率带相差93 Hz，且故障频率两侧边频带各谱线之间的间隔为11 Hz左右，与保持架旋转频率fc=Rifs/(Ri+Ro)=10.76 Hz吻合。文献[15]研究表明，滚动体损伤在滚动体故障特征频率的各阶倍频处有幅值逐渐下降的谱线，且以各阶倍频为中心，在两旁有间隔等于保持架频率的调制谱线。以上结果符合这一结论。

4 轴承振动实验分析

结合列车转向架轴箱轴承的实际使用环境不同于一般轴承，其外圈上半区承载，而内圈随同车轴转动，设计的实验装置如图7所示。主要包括调速电机与控制箱、增速箱、转轴、支撑轴承和加载装置等。支撑轴承外伸端安装实验轴承，外圈压力由三根弹簧提供，通过可动水平压板加载于轴承。转轴实验转速可达到2 340 r/min，这里主要分析转速为1 590 r/min的实验结果。加速度传感器安装在可动水平压板及加载台架上，测量外圈的垂向振动。

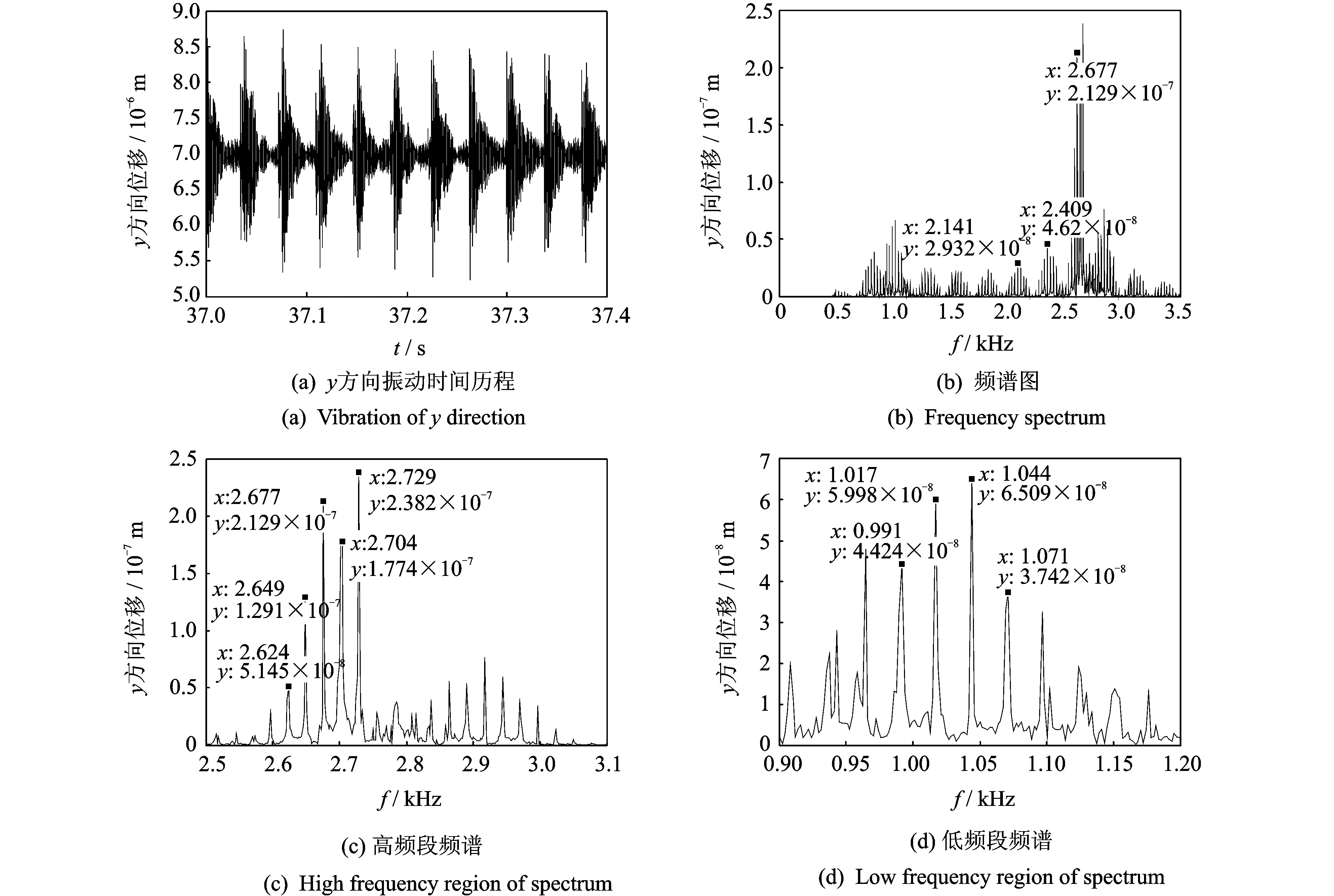
图5 内圈故障轴承振动特性Fig.5 Vibration characteristics of bearing with inner race fault

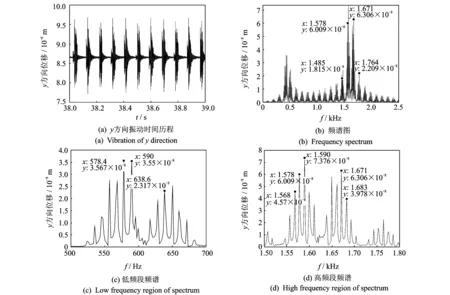
图6 滚动体故障轴承振动特性Fig.6 Vibration characteristics of bearing with rolling element fault

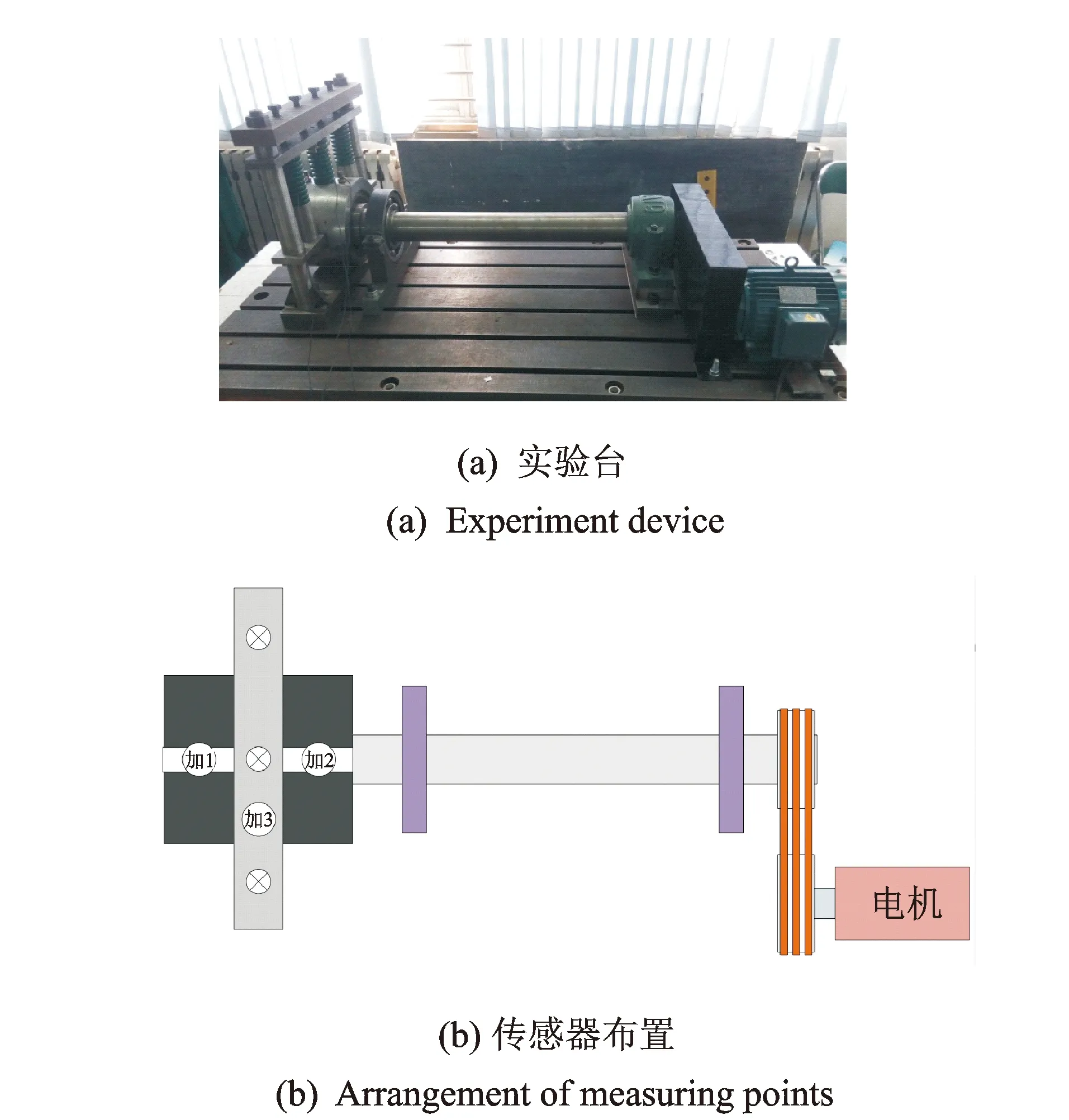
图7 实验装置和测点布置Fig.7 Experiment devices and arrangement of measuring points

4.1 正常轴承

图8为满载状态下竖直方向的振动加速度时间历程以及对应频谱。从频谱图可以看到，转子旋转频率26.73 Hz及其各阶倍频(如53.74，106.93 Hz等)的存在，同时以182.74 Hz为轴承的变柔度振动频率与理论计算以及数值仿真结果吻合。图中出现的其他频率为支撑轴承产生的振动频率，对实验对象无影响。

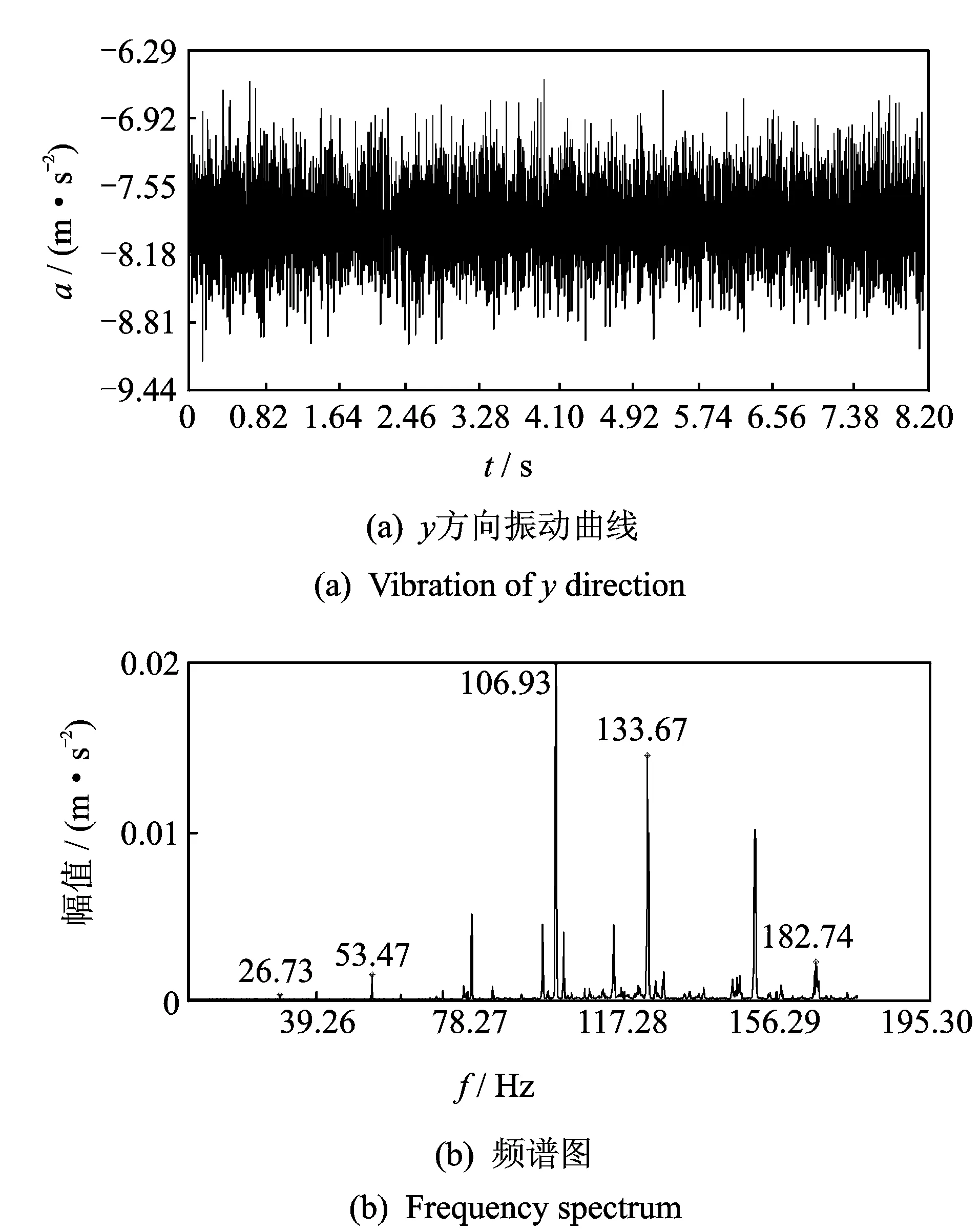
图8 正常轴承实验结果Fig.8 Experiment analysis of bearing with no fault

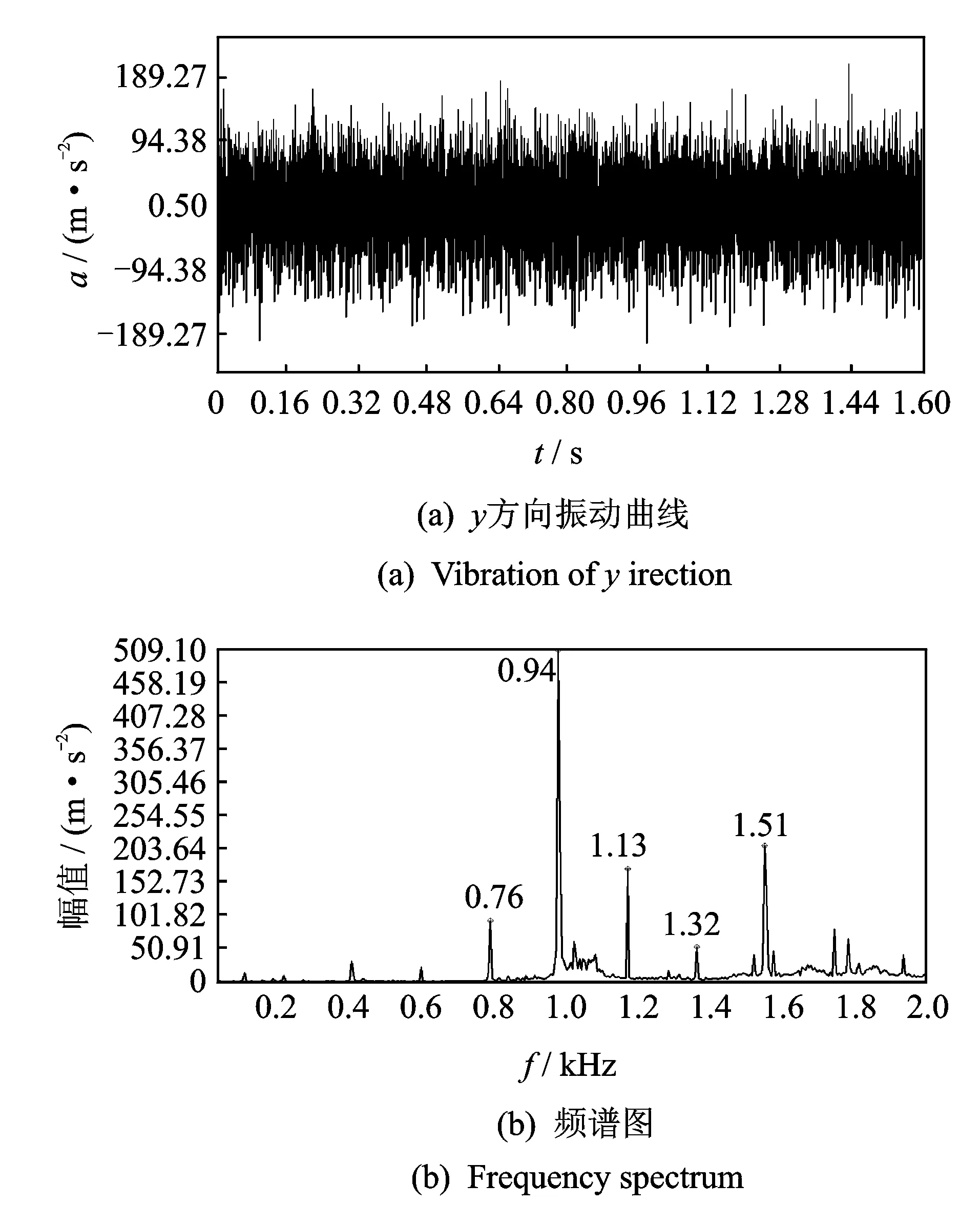
图9 外圈故障轴承实验结果 Fig.9 Experiment analysis of bearing with outer race fault

4.2 外圈故障轴承

为了模拟轴承外圈剥离等故障，在轴承外圈内部沿轴向加工了宽度为25 mm，深度为1 mm的损伤区。轴承安装时保证故障所在角位置大约为5.5 rad，与数值仿真条件相同，如图9所示。从频谱图中可以看到外圈故障频率190 Hz以及幅值较大的倍频成分940，1 130和1 320 Hz等，与理论计算结果误差仅为2.5%。

4.3 内圈故障轴承

对轴承内圈上，沿轴向加工了深约为1 mm、宽约为5 mm的损伤区，实验得到振动加速度时间波形及频谱如图10所示。可以看到，中心频率1 040，1 290，1 550及1 810 Hz相差均为260 Hz左右，为内圈故障特征频率fi，与理论故障频率256.2 Hz相吻合，误差为1.5%。各中心频率两侧出现间隔均为20～30 Hz左右的边频成分，为内圈转动频率，如图(c)中1 290 Hz两侧的1 260和1 320 Hz，1 550 Hz两侧的1 530和1 570 Hz等。

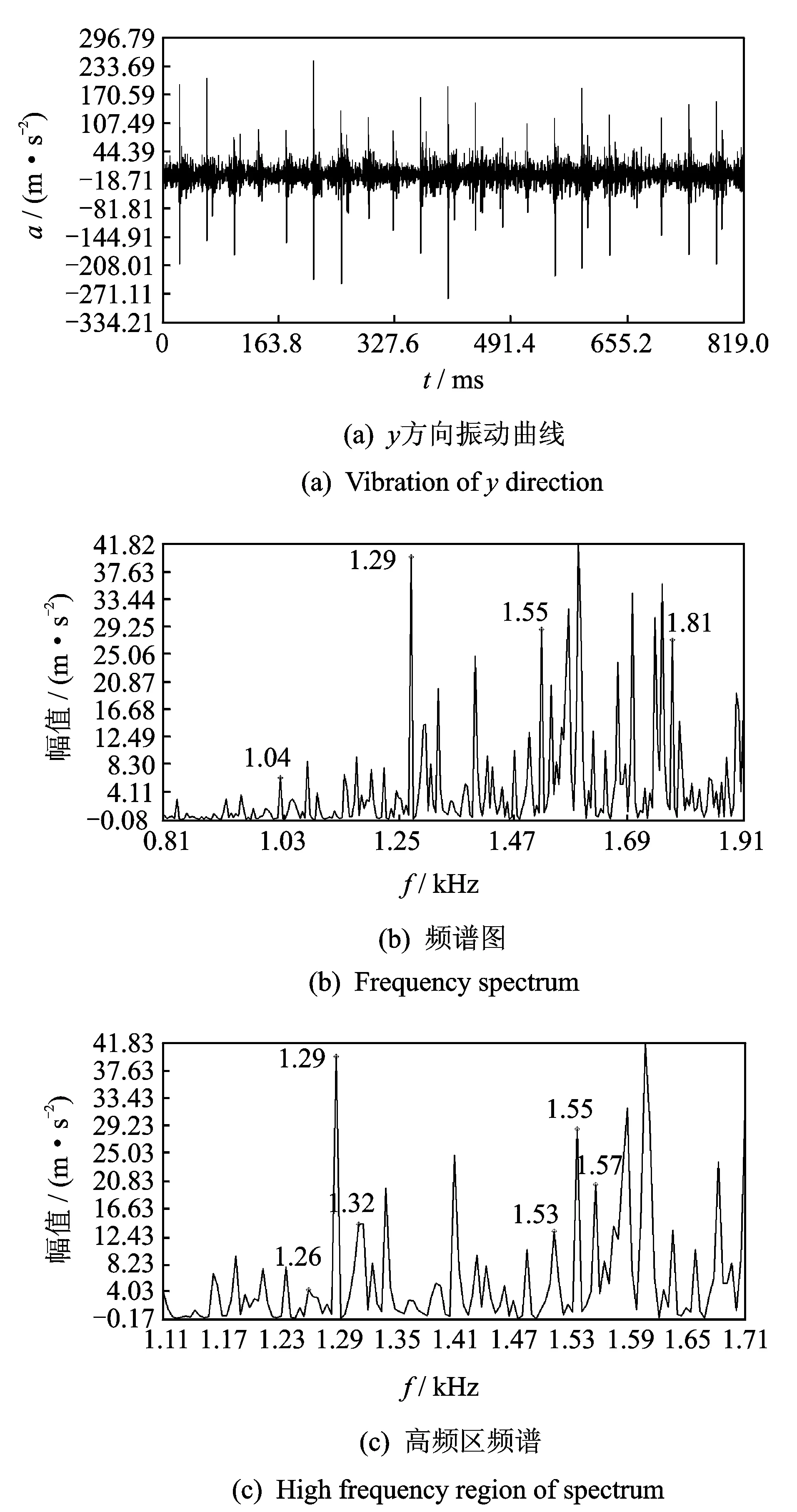
图10 内圈故障轴承实验结果 Fig.10 Experiment analysis of bearing with inner race fault

4.4 滚动体故障轴承

在滚动体上加工了沿母线剥离深度为1.5 mm的凹坑，实验得到振动加速度时间波形及频谱图如图11所示。可以看到，中心频率1 470，1 560，1 650及1 750 Hz相差均为90 Hz左右，为滚动体故障特征频率fr，与理论故障频率92.8 Hz基本吻合，误差为3%。各中心频率两侧出现间隔均为10 Hz左右的边频成分，为内圈转动频率，如图11(c)中1 650 Hz两侧的边频成分1 660 Hz和1 670 Hz等。

4.5 不同程度损伤故障的比较

轴承各部位剥离等损伤由早期的点蚀发展而来，且随轴承使用而逐渐加深。损伤程度的不同，对于轴承工作状态和造成的振动特征均有影响。以滚动体损伤为例，加工了从轻微到严重级别的损伤故障。轻微故障包括中部剥落(平均深度为0.3 mm)和端部剥落(平均深度为0.5 mm)。中等故障包括一个滚动体剥落和另一个滚动体点蚀两种故障的叠加，重度故障包括表面三块剥落区域(深度分别为0.5，0.4和0.3 mm)，三块面积区域通过沟槽联通，以及沿滚动体轴线有沟槽(深约为0.8 mm，宽约为1 mm)和周围剥落两块面积(深度为0.2 mm)。

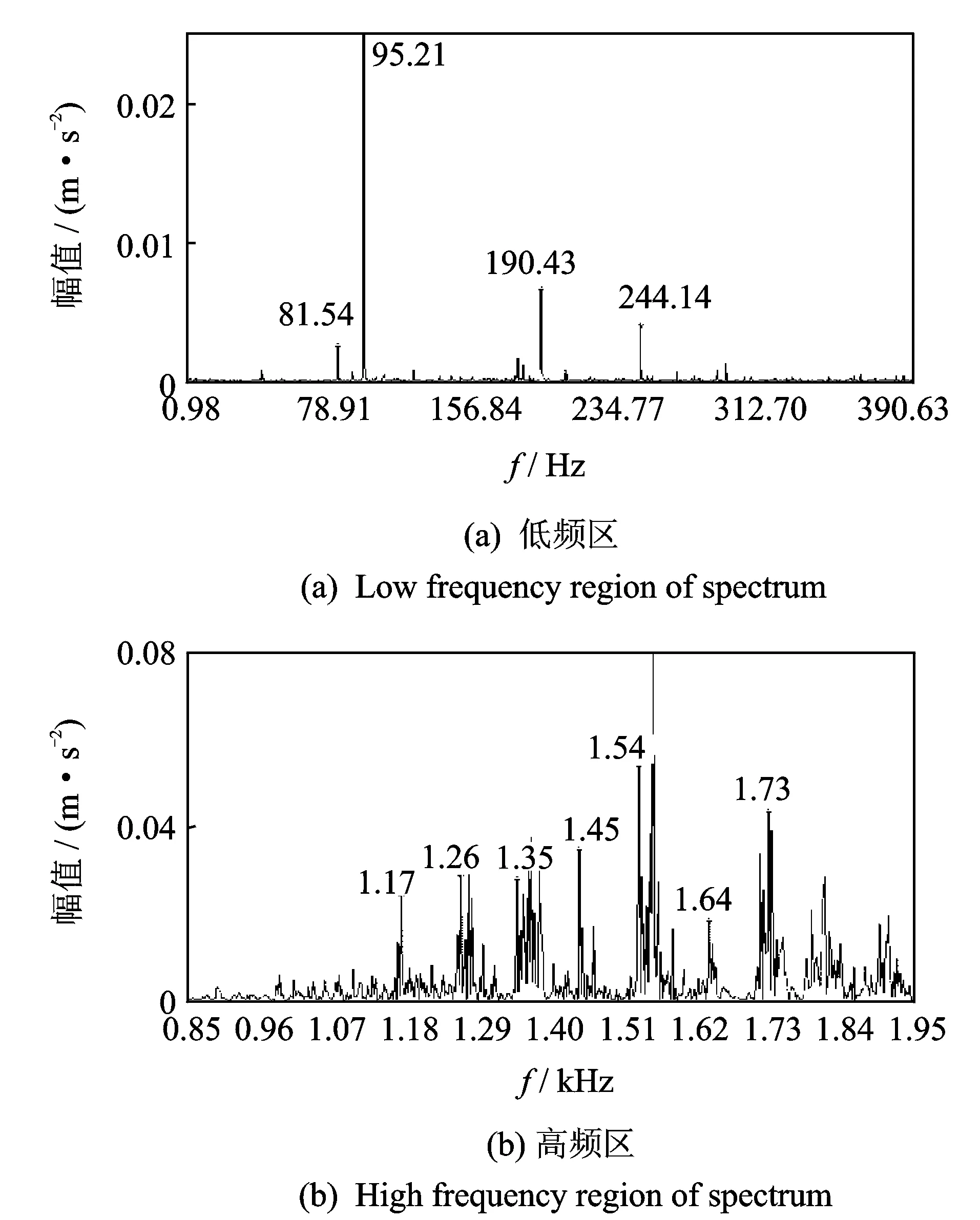
图12 轻微滚动体故障Fig.12 Slight fault of rolling element

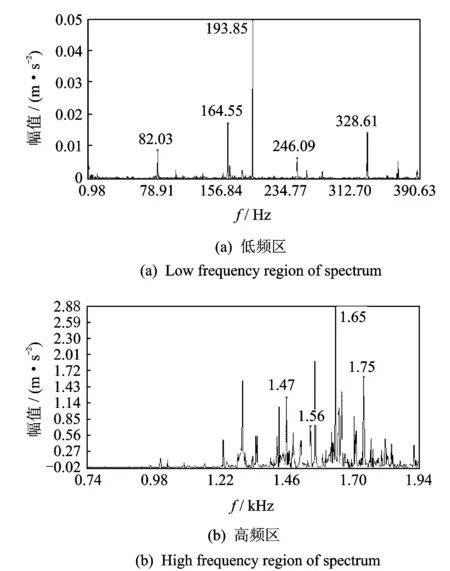
图13 中度滚动体故障Fig.13 Moderate fault of rolling element

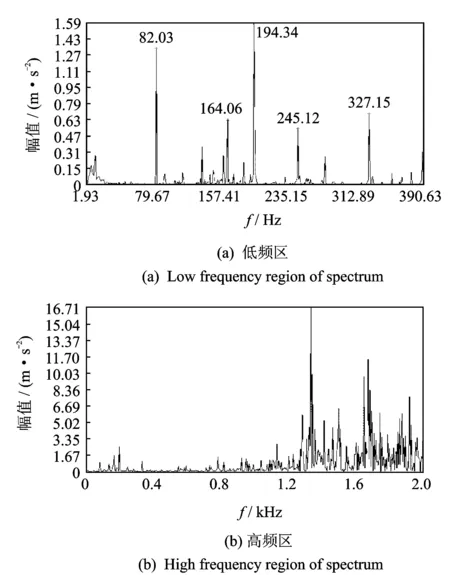
图14 重度滚动体故障Fig.14 Severe fault of rolling element

图12～14分别为3种损伤故障轴承的频谱图，分别给出了低频和高频区的故障特征。从图12(a)可以看到，滚动体故障频率为95.21 Hz，其他频率成分为转子支撑轴承的变柔度振动频率81.54 Hz及其倍频，与实验轴承无关。图12(b)为高频区故障特征，出现了以故障频率90 Hz为间隔的一系列谱线，且中心频率两侧出现以保持架旋转频率为间隔的谱线。图13(a)为中度故障的低频谱线，可以看到与图12(a)的区别在于95.21 Hz消失，193.85 Hz出现。因95.21 Hz故障频率只计算了故障对外圈的冲击影响而忽略了故障对内圈的冲击传递到外圈的影响，随着故障加深，内外圈滚过故障产生的冲击激励也在增强，故障对于内圈的冲击增大而传递到外圈，所以相比于轻微故障相当于造成了两次冲击，故障频率加倍。图13(b)的高频频谱规律性比图12(a)有明显减弱，以故障频率为间隔的谱线存在但不明显。图14(a)为重度故障低频频谱，相比前两种故障情况，低频出现很多杂乱谱线，且主要频率幅值显著增大，图14(b)因故障冲击太大，谱线已相当杂乱。

对滚动体不同程度损伤的研究结果表明，滚动体早期故障对外圈的冲击相比对内圈的冲击容易检测，发现故障信号需对轴承进行更换，故建立故障模型时不考虑损伤与内圈的冲击，符合工程实际。

5 结 论

1) 轴承在正常工作状态下变柔度振动较明显，不同故障类型表现出不同的故障特征频率，且内圈及滚动体故障频率均受到调制。

2) 故障在不同的发展阶段，轴承的振动频谱区别很大，其中早期故障的特征频率在频谱中较明显，随着故障破坏程度的加剧，冲击激励变大影响到轴承其他部位，故障频率变得难以区分。

3) 正常情况下轴承振动信息中包含大量噪声干扰，要准确提取故障特征频率，判断故障类型，应对振动信号进行进一步处理。

4) 针对动车组轴承的研究，为该类轴承的故障诊断及检测提供了理论依据。

[1] 王灿，王嘉乐，会强，等.Hilbert-Huang变换在机车滚动轴承故障诊断中的应用[J].振动、测试与诊断，2013,33(S1)：184-187.

Wang Can，Wang Jiale，Hui Qiang，et al. Application of fault diagnosis of locomotive rolling bearings based on HHT of LabVIEW[J]. Journal of Vibration，Measurement & Diagnosis,2013,33(S1):184-187.(in Chinese)

[2] 聂晔.动车组转向架轴承可靠性分析与故障诊断的技术研究[D].长沙：中南大学，2011.

[3] 曹青松，朱志强，叶征春，等.动车组滚动轴承非线性动力学特性分析[J].轴承，2013(8)：8-11.

Cao Qingsong，Zhu Zhiqiang，Ye Zhengchun，et al. Analysis on nonlinear dynamic characteristics of rolling bearings for multiple unit trains[J]. Bearing，2013(8)：8-11.(in Chinese)

[4] 颜家森，朱龙泉，赵三星，等.高速铁路轴箱轴承载荷分布分析[J].轴承，2012(10):12-16.

Yan Jiasen,Zhu Longquan，Zhao Sanxing，et al. Analysis on load distribution of high-speed railway axle box bearings[J]. Bearing，2012(10)：12-16.(in Chinese)

[5] 关贞珍，郑海起，王彦刚，等.滚动轴承局部损伤故障动力学建模及仿真[J].振动、测试与诊断，2012，32(6)：950-955.

Guan Zhenzhen，Zheng Haiqi，Wang Yangang，et al. Fault dynamic modeling and simulating of rolling bearing with localized defect[J]. Journal of Vibration，Measurement & Diagnosis，2012，32(6)：950-955.(in Chinese)

[6] 曹宏瑞，李亚敏，成伟，等.局部损伤滚动轴承建模与转子系统振动仿真[J].振动、测试与诊断，2014，34(3)：549-552.

Cao Hongrui，Li Yamin，Cheng Wei，et al. Rolling bearing modeling with localized defects and vibration response simulation of rotor-bearing system[J]. Journal of Vibration，Measurement & Diagnosis，2014，34(3)：549-552.(in Chinese)

[7] 张建军，王仲剩，芦玉华，等.基于非线性动力学的滚动轴承故障工程建模与分析[J].振动与冲击，2010，29(11)：30-34.

Zhang Jianjun，Wang Zhongsheng，Lu Yuhua，et al. Nonlinear dynamic modeling for localized defects in a rolling element bearing[J]. Journal of Vibration and Shock，2010，29(11)：30-34.(in Chinese)

[8] 陈恩利，于雪梅，申永军，等.奇异性检测在滚动轴承外圈损伤故障诊断中的应用[J].轴承，2006(5)：28-30.

Chen Enli，Yu Xuemei，Shen Yongjun，et al. Application of singularity detection to outer ring damage diagnosis of rolling bearings[J]. Bearing，2006(5)：28-30.(in Chinese)

[9] 东亚斌，廖明夫，高琦.滚动体具有局部缺陷滚动轴承的动力学分析[J].重型机械，2012(3)：148-152.

Dong Yabin，Liao Mingfu，Gao Qi. Dynamics analysis on rolling element bearings with localized defects[J]. Heavy Machinery，2012(3)：148-152.(in Chinese)

[10]Tandon N, Choudhury A. An analytical model for the prediction of the vibration response of rolling element bearings due to a localized defect [J]. Journal of Sound and Vibration，1997，205:275-292.

[11]杨咸启，刘文秀.圆锥滚子轴承动态刚度分析[J].轴承，2002(2)：1-3.

Yang Xianqi，Liu Wenxiu. Analysis of dynamic stiffness of tapered roller bearing[J]. Bearing，2002(2)：1-3.(in Chinese)

[12]谢军太，弥宁，黄建龙.径向定载条件下圆柱滚子轴承的振动分析[J].振动、测试与诊断，2013，33(S1)：176-179.

Xie Juntai，Mi Ning，Huang Jianlong. Vibration analysis of cylindrical roller bearings under the fixed radial load condition[J]. Journal of Vibration，Measurement & Diagnosis，2013,33(S1)：176-179.(in Chinese)

[13]罗继伟，张俊杰.圆锥滚子接触应力数值分析[J].轴承，2004(9)：1-3.

Luo Jiwei，Zhang Junjie. Numerical solution of contact stress of tapered roller bearing[J]. Bearing，2004(9)：1-3.(in Chinese)

[14]王彦伟，罗继伟，陈立平.圆锥滚子轴承接触分析[J].华中科技大学学报：自然科学版，2007，35(9)：19-21.

Wang Yanwei，Luo Jiwei，Chen Liping. Analysis of the contacts of taper roller bearings[J]. Journal of Huazhong University of Science & Technology:Nature Science Edition，2007，35(9)：19-21.(in Chinese)

[15]梅宏斌.滚动轴承振动监测与诊断[M].北京：机械工业出版社，1996.

[16]Fukata S, Gad E H, Kondou T, et al. On the radial vibration of ball bearings (computer simulation) [J]. Bulletin of the JSME, 1985, 28: 899-904.

10.16450/j.cnki.issn.1004-6801.2016.04.009

国家自然科学基金资助项目(11272228,11332008)；高校博士点专项科研基金资助项目(20120032110011)；天津市自然科学基金资助项目(13JCZDJC34900)

2014-07-10；

2014-12-01

TH133

杨天蕴，男，1989年5月生，硕士生。主要研究方向为非线性动力学、机械振动与仿真分析。

E-mail：tianlavigne@163.com

简介：丁千，男，1963年4月生，教授。主要研究方向为动力学与控制。E-mail:qding@tju.edu.cn