大悬伸状态加工水室封头重型铣削振动分析

程耀楠， 巩亚楠， 刘 利， 敖晓春， 刘亦智， 刘立佳

(哈尔滨理工大学高效切削及刀具国家地方联合工程重点实验室 哈尔滨， 150080)



大悬伸状态加工水室封头重型铣削振动分析

程耀楠， 巩亚楠， 刘 利， 敖晓春， 刘亦智， 刘立佳

(哈尔滨理工大学高效切削及刀具国家地方联合工程重点实验室 哈尔滨， 150080)

针对大悬伸状态下加工水室封头产生的重型铣削振动，以重型铣削水室封头现场加工实验为基础，分析重型铣削振动产生的原因，并根据现场实验对工件已加工表面形貌进行对比分析。建立重型铣削刀具偏心跳动模型、刀具与主轴系统的轻微变形模型和进给系统刚度的模型，分析其对重型铣削瞬时切削厚度的影响，同时建立重型铣削力数学模型和铣削轨迹模型。分析重型铣削系统振动影响因素及规律，振动模型预测结果与实验结果吻合较好。该工作为进一步研究重型铣削振动特性提供依据。

振动分析； 表面形貌； 大悬伸； 重型铣削； 水室封头

引 言

第3代核岛(AP1000)蒸发器水室封头是目前世界上最先进、设计制造难度最大的三代核电锻件，水室封头部件作为核电站核岛一回路的容器，是蒸汽发生器的关键部件。由于锻造技术手段无法实现成型锻造，只能先锻造出一个近似的长方柱体，全部由机械加工来完成，材料为508III钢，金属去除率达到70%左右。超大型水室封头锻件切削加工属极端制造领域超重型切削，其进给量和背吃刀量是中型切削的10余倍，切削力是中型切削的40～50倍。其外表面有许多大型锻造零部件类似的锻造缺陷，如锻造铲沟、锻造裂纹、锻造褶皱以及夹砂夹杂等，引起零件加工余量的严重不均[1]。由于508III钢具有高强度、高硬度和高断面收缩率等特性，在超大进给量、背吃刀量与切削力的情况下，处于极限悬伸状态的主轴与刀具产生巨大振动，严重降低生产效率并影响表面加工质量。同时，机床的振动还会造成机床系统过早出现疲劳损坏，使机床的安全性、稳定性和生产强度下降。因此，如何降低重型铣削水室封头在加工过程中的振动成为研究重型铣削加工的新挑战。

由于铣削振动作为影响机床使用性能和工件加工质量的重要因素，故一直是研究铣削振动领域的研究热点。一般情况下，通过对铣削振动特性进行假设，将实验过程假设为理想的铣削加工过程，同时以切削力与瞬时切削厚度的关系作为力-振动的闭环传递函数为表现形式的动力学模型的桥梁[2]。大多数研究很少用到精确的瞬时切削厚度与刀具轨迹，而是假设在理想铣削过程中进行表面形貌仿真，因而假设和仿真无法准确反映真实的切削振动状态[3]。由于重型铣削加工的特殊性，实验室环境不能复现重型铣削加工过程，实验室数据无法真实表征重型铣削振动状态[4]，因此国内外学者对于重型铣削振动的深入研究成果较为少见。

笔者根据重型铣削水室封头的实际加工特点，分析重型铣削振动状态下悬伸改变量对已加工表面形貌的影响，同时借助建立的模型对重型铣削振动的产生及影响因素进行分析。

1 重型铣削振动产生机理与实验设计

1.1 重型铣削振动产生原因

根据现场调研结果可知，重型铣削振动主要来源于3个方面。

1) 机床机构产生的振动。机床机构自身存在制造误差和传动误差等问题，在空转状态下也产生较大的振动。同时，在实际切削加工过程中机床的进给机构在运行时也经常发生有摩擦的自激振动、快速进给过程中的残余振动等。

2) 机床外部振源引起的振动。在实际生产条件下，机床由统一导轨连接，多台机床共同加工时产生共振效应。

3) 切削加工引起的振动。铣削加工自身具有断续加工的特点，又由于铣削加工508III钢，在超大进给和背吃刀量的情况下受到超大切削力的激励，主轴的悬伸量经常处于机床的极限伸长量，导致在加工过程中伴随着巨大振动。事实上，机床机构产生的振动和切削加工引起的振动并非相互独立存在，而是紧密联系的。机床机构产生的振动与铣削加工中的刀具和工件的相对振动具有耦合效应，从而使振动更加剧烈，导致已加工表面出现波纹状走刀轨迹，造成刀片严重的冲击破损与磨损。

1.2 重型铣削振动现场实验设计

根据重型铣削振动产生的特点，考虑到重型铣削水室封头外球面工序包括了刀具与主轴系统的整个悬伸长度区间，因此实验选择在重型铣削水室封头外球面工序时进行。机床型号为TK6920型数控落地镗铣床(镗轴直径为200mm，主轴箱行程为5 000mm，滑枕行程为1 200mm)，刀盘选用Φ200R8圆弧刀片刀盘(WIDIA-M100型)，刀片为可转位圆刀片(RCMT1606MO-43)，水室封头材料为508III钢。实际加工参数如下：切削速度为250m/min(转速为398r/min)，切削深度为2mm，进给速度为1 100mm/min。数据采集分析系统采用东华DH5922信号采集系统，并将PCB加速度传感器测量铣削时x，y，z向的振动信号。现场大悬伸铣削实验如图1所示。

图1 现场大悬伸铣削实验Fig.1 Field milling experiment of large overhanging

2 重型铣削振动影响下已加工表面形貌分析

重型铣削水室封头实验根据实际加工参数，刀具以二维次圆弧轨迹进给，去除工件铣削区域材料并形成已加工表面。由于实验中主轴悬伸量逐渐增大，铣削轨迹圆弧也依次增大，大部分已加工表面波纹都不能被后续切削刃和刀路轨迹包络面去除，因此在主轴大悬伸量情况下，已加工表面残留区域形成较大的振动波纹，如图2所示。图2(a)为多次走刀得到的半圆形已加工表面。整个实验加工半球面切削参数均相同，但半球面上得到若干不同的已加工形貌区域，且随着主轴悬伸量的变化而改变。根据主轴悬伸量由小及大的顺序，提取出主要的3个区域的已加工表面形貌，如图2(b)所示。

图2 重型铣削水室封头已加工表面形貌Fig.2 Machined surface appearance of heavy milling water chamber head

铣削区域对应的主轴悬伸长度如表1所示。Ⅰ区已加工表面形貌较为规整且表面起伏较小，但实际轮廓轨迹存在细微波纹。Ⅱ区已加工表面轮廓光滑且顶峰尖锐。由于在铣削Ⅱ区时更换新的刀齿，刀齿较为锋利且完整性较好，但刀齿切削厚度严重不均。Ⅲ区得到的已加工表面刀齿切削厚度极为不均，刀齿轨迹叠加较为繁杂。由于铣削过程中部分刀齿破损，刀齿轮廓轨迹存在细小摩擦波纹与材料撕裂痕迹，且部分刀齿轨迹平面偏离工件法球面。同时，主轴悬伸量的增大使整个系统的稳定性降低。铣削区域的表面波纹主要是刀齿在进给运动和振动状态共同影响下的已加工表面轮廓形状，但刀具与工件间的相对振动是形成轮廓的主要原因[5]。

表1 铣削区域对应主轴悬伸长度

重型铣削水室封头加工过程中已加工表面微观形貌的形成主要取决于刀具和工件之间的相互干涉。加工过程中工件表面微观形貌严重影响机床机构间的摩擦磨损、配合性能和传动精度等，直接影响机床的使用性能，同时会激起整个加工系统的振动。在实际加工过程中，为了提高生产效率和单位时间内材料的去除率，从而增大切削用量。这使得切削振动加剧，导致加工零部件的表面精度和刀具寿命降低，甚至严重时整个加工过程伴有剧烈的颤振，破坏整个加工系统的稳定[6]。

3 重型铣削振动模型分析

由于重型铣削刀具尺寸较大，存在制造与安装误差、刀盘与主轴系统刚度的影响，因此在重型铣削过程中会存在轴向几何中心与刀具转动中心不一致的现象。重型铣削加工过程中主轴悬伸量非常大，在巨大切削力的激励下，增大了主轴与刀盘系统的圆跳动与摆动，加剧了刀具的偏心量和刀具与主轴系统变形，造成的切削力突变还会引起进给系统发生进给位移偏差。对于重型铣削加工过程，刀具偏心跳动在单一铣削周期内不会引起总的切削去除量的改变，但严重影响刀具的切入切出状态和瞬时切削厚度，使刀盘上每个刀片受到的力并不相同，在位置角不变的情况下各刀片受到的突变铣削力最终会引起整个重型铣削系统振动加剧。因此，需要对重型铣削刀具偏心跳动、其与主轴系统的轻微变形和机床进给系统刚度问题的影响分别进行分析。

3.1 重型铣削刀具偏心跳动模型

常见的重型铣削刀具偏心跳动主要分为3类[7]，如图3(a)所示。第1类，刀具旋转中心与刀具的几何中心发生了平行偏移；第2类，刀具转动中心轴线偏移轴向几何中心为某一角度(同一平面)；第3类，在第1类的基础上，刀具转动中心轴线偏移轴向几何中心线为一定空间(不同平面)夹角。在铣削名义运动轨迹理论中，侧铣刀具轴线相对于工件表面法向的倾斜角度变化较小，经过工件表面且与参与切削刀刃的刀具轴向位置分布基本相同。在重型铣削加工过程中，刀具与主轴系统在大悬伸量和超大铣削力的激励下产生较大的动态响应，刀具偏心跳动较为严重，形成的振动位移附加在刀具名义运动轨迹上。根据重型铣削刀具偏心跳动模型，结合加工过程中刀具每齿进给方向与横向进给方向，建立对应重型铣削刀具偏心跳动条件下已加工表面形貌的铣削轨迹模型，如图3所示。

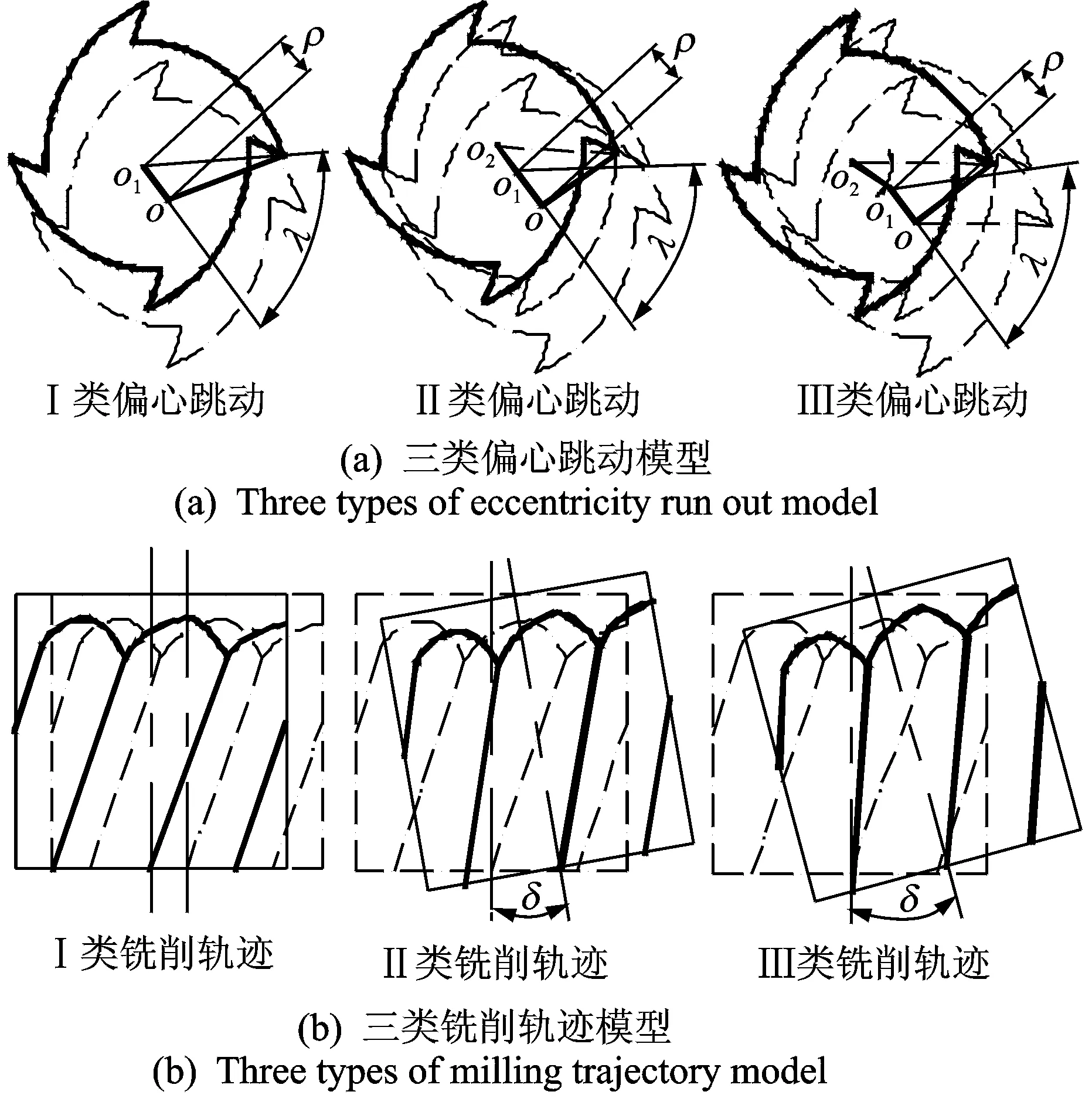
图3 刀具偏心跳动与铣削轨迹模型Fig.3 Cutter eccentricity run out and milling trajectory geometry model

如图3所示，在刀具偏心跳动存在的情况下，刀具中同一刀片或不同刀片之间不同铣削微元的切削轨迹与刀具的理论铣削轨迹并不同，实际切削半径随着微元位置的改变而变化。通常情况下分析刀具偏心跳动时，只考虑刀具轴线相对于旋转轴线的偏移。在普通铣削加工中，刀具的偏心量ρ一般为μm数量级，远小于刀具半径，只需考虑第1类刀具偏心跳动模型。铣削单元高度用Ht,l表示时，获得的第1类偏心跳动的微元铣削半径[8]为

(1)

其中：ρ为刀具偏心量；β为刀齿轴向偏转角；λ为变心方向角；D为刀具直径；fZ为每齿进给量；t为刀齿编号；φ为刀具旋转角；N为刀齿数。

重型铣削加工时刀具偏心跳动复杂程度与数量级远远大于普通加工刀具的偏心量，在分析重型铣削刀具偏心跳动时，应考虑第2类和第3类刀具偏心跳动。由于第2类偏心跳动是第3类偏心跳动的一种特殊情况，因此在主轴大悬伸量情况下，应考虑第3类刀具偏心跳动来保证足够的精度。根据式(1)，同时考虑到刀具平移方向夹角λ、安装后刀具的径向长度L、刀具倾斜方向与平移方向的夹角λt和刀片的倾斜角度δ，得到第3类刀具偏心跳动的微元铣削半径为

(2)

3.2 重型铣削刀具与主轴系统轻微变形模型

主轴处于较大悬伸状态且伴随着刀具巨大的偏心跳动，成为影响铣削振动的重要原因之一，然而在重型铣削加工水室封头过程中,刀具与主轴系统的变形和进给系统刚度成为制约铣削振动与表面精度不可忽略的重要因素。在重型铣削过程中，虽然铣刀直径较大，主轴与机床的刚度较高，但是重型铣削刀具与主轴系统处于大悬伸状态且主轴结构为阶梯伸缩轴。在大切削力与振动冲击的激励下，刀具与主轴系统极易发生轻微变形，进而加剧刀具的偏心跳动。因此，重型铣削过程刀具与主轴的轻微变形成为影响重型铣削振动和制约铣削表面精度不可忽略的重要因素，也是铣削区域表面形貌误差产生的重要原因[9]。

由于阶梯主轴直径与刀盘直径差异较大，因此根据铣削工件不同部位主轴悬伸量的变化，将刀具与主轴系统简化为二阶截阶梯状悬臂梁结构[10]，得到刀具与主轴系统变悬伸受力模型，如图4所示。

考虑到切削刃受到的切削力区域长度lc相比刀具与主轴悬伸长度可等价为一个集中力F，集中区域位于z轴的长度近似为滑枕与刀齿的距离L。根据传统铣削弹性变形的分析方法，将刀具与工件系统在z轴向l处受力径向弹性变形可简化为x和y方向上挠度值，即

(3)

根据虚位移原理[11]，刀盘与主轴系统在z轴向l处受铣削力作用发生的柔性变形可简化为

(4)

重型铣削在超大切削力激励下刀具与主轴系统轻微变形量可表示为

(5)

图5 刀齿瞬时切削厚度模型Fig.5 Instantaneous cutting thickness model of cutter tooth

刀具与主轴系统轻微变形与重型铣削微元瞬时切削半径的关系为

(6)

(7)

为了简化重型铣削瞬时铣削半径公式，忽略变形对θs的影响，将式(5)代入式(6)，得到包含刀具偏心跳动和刀具变形时重型铣削微元瞬时切削半径表达式为

(8)

3.3 重型铣削机床进给系统刚度模型

重型铣削水室封头加工过程属于强力切削加工的范畴，因此在超大铣削力和机床机构自身的弹性作用下，机床进给系统在x，y方向不可避免的会发生一定的位置偏移，直接影响刀齿切削轨迹和铣削厚度，引起铣削力大小的突变，并影响机床的进给机构在加工过程中发生有摩擦的自激振动和快速进给时的残余振动等。机床进给系统刚度分为轴向刚度和扭转刚度。进给系统的轴向刚度反映了进给系统抵抗轴向变形的能力，是指滚珠丝杠副、支承轴承等进给系统的综合拉压刚度[13]。根据机床进给系统的组成，建立机床进给系统轴向刚度简易模型如图6所示。

图6 机床进给系统轴向刚度简易模型Fig.6 The simple axial stiffness model of machine feeding system

TK6920型数控落地铣镗床丝杠两端都采用NSK公司的丝杠专用轴承，采取预拉伸结构安装方法，通过简易模型，由串、并联的刚度系数计算方法得到进给系统轴向刚度[14]KZ为

(9)

其中：KS为进给丝杠的轴向刚度；KB为并联轴承的轴向刚度；KL为螺母组件的轴向刚度；KLZ为螺母座的轴向刚度；KC为进给传递机构的轴向刚度。

(10)

其中：KC1，KC2为丝杠两端支承轴承的轴向刚度；KZ1，KZ2为两端轴承座轴向刚度；KCS1为螺母左边丝杠轴向刚度；KCS2为螺母右边丝杠轴向刚度。

机床系统的扭转刚度反映了进给系统抵抗扭转变形的能力。根据扭转理论得到进给系统扭转刚度[15]为

(11)

其中：KφS为滚珠丝杠的扭转刚度；KφD为伺服电机的扭转刚度；KφZ为支承轴承的扭转刚度；KφC为进给传递机构的扭转刚度。

建立轴向变形和扭转变形模型，进给位移偏差可表示为

(12)

其中：wj为进给系统的位移偏差；Kδ为切削力与力矩的转换系数；Kε为转角与轴向位移变换系数。

4 瞬时铣削厚度函数的重型铣削力模型

通过建立重型铣削刀具偏心跳动模型、刀具与主轴变形模型和进给系统刚度模型，得到重型铣削瞬时切削半径的表达式为

(13)

重型铣削瞬时切削厚度数学模型表示为

(14)

切削层厚度是指在基面内度量的相邻刀齿的主切削刃运动轨迹间的距离[16]。由于重型铣削水室封头外球面采用侧面铣削工艺，因此加工过程中铣削层厚度不断变化。考虑重型铣削加工的复杂性，不同刀齿在切削过程中切削厚度差异较大。

(15)

由于微元的瞬时切削厚度不同，切削力系数随着微元变化而改变，因此建立有关切削厚度的瞬时铣削力系数表达式为

(16)

其中：T0，T1，R0，R1，A0和A1均为常数，受刀具、工件、主轴转速和工件材料等影响，几乎不受每齿进给量、轴向切深和径向切深的影响；dZ为微元轴向高度；φ为刀具旋转角；N为刀具齿数；M为每齿微元数。

将切削微元受力表示成x，y，z轴向经典铣削力方程为

(17)

其中：θt,l(φ)为微元(t,l)的瞬时角位置。

重型铣削水室封头实验工程中，选用统一的实验参数且不改变刀盘中刀具安装次序，只对可转位刀具进行3次位置转换，同时铣削位置对应3个不同悬伸量，考虑到加工过程中个别刀片的冲击破损程度始终大于刀盘中的其他刀片，因此选取破损最严重的刀片进行分析，如图7所示。超景深显微镜测量3组破损数据如表2所示。

图7 偏心跳动作用下刀具的冲击破损与磨损Fig.7 Breakage and wear of the cutter under the influence of eccentric run out

Tab.2 Shock breakage and wear of the tool′s cutting edge

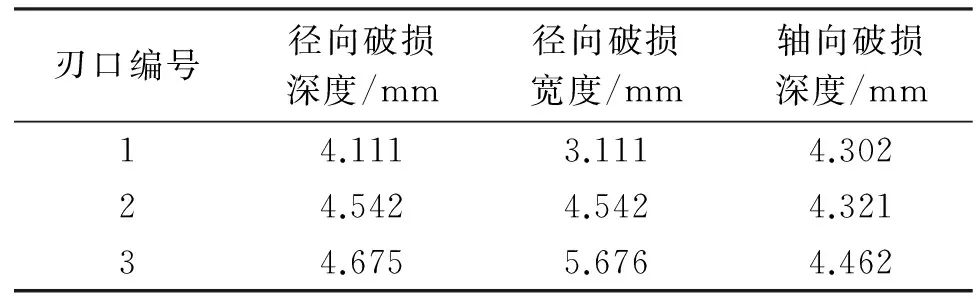
刃口编号径向破损深度/mm径向破损宽度/mm轴向破损深度/mm14.1113.1114.30224.5424.5424.32134.6755.6764.462

实验过程中，前刀面与后刀面破损深度反映出重型铣削实验过程中的偏心跳动量。考虑到铣削加工断续切削的特点，同时在重型铣削偏心跳动严重的情况下，刀具前刀面承受巨大的冲击力，前刀面表层材料极易在冲击过程中发生大面积脱落，进而影响数据的准确性，因此选用后刀面轴向破损深度作为参考实验数据。通过观察刀面的刃口断裂情况可知，三处切削刃除1号螺纹孔处出现冲击性材料脱落外，其余切削刃口的冲击破损皆为长期冲击和磨损情况下形成的，考虑到重型铣削刀盘刚度较大，在此不考虑刀盘的变形，刀片的最大破损深度可视为刀盘在偏心跳动最大值。

轴向刀具极限偏心跳动量为

(18)

其中：hap名义切削厚度；α为刀片后角；Rj1(t,l)，Rj2(t,l)，Rj3(t,l)为轴向破损深度。

将表2数据代入式(18)，得到重型铣削存在刀具偏心跳动的微元铣削半径范围

7.98≤Rt,l≤12.251

(19)

假设重型铣削过程中重型铣削力激励下产生的振动为振动系统中主要的振动源，则振动振幅与瞬时铣削力成正比，同时瞬时切削厚度变化导致铣削力的突变，因此铣削力可以分解为理论值和刀偏心跳动附加值两部分。无论切削力系数取值是常数或者是有关瞬时切削厚度的函数，二者关系始终可以表示为

(20)

其中：Fit,l(φ)为实际瞬时切削力；Fi为名义切削力(i取x,y,z)；Amax为振幅极值；A为名义振幅。

(21)

结合式(17)和式(19)整理得到极限偏心跳动下的极限切削力与名义铣削力的关系为

(22)

由式(22)可知，重型铣削水室封头加工过程在极限偏心跳动状态下，极限切削力远大于名义铣削力。在以切削力为主要激振源的振动系统中，极限振幅与铣削力成正比关系。

重型铣削机床的制造与安装误差造成重型铣削加工过程中发生不可避免的偏心跳动。根据重型铣削刀具偏心跳动模型和刀具-主轴变形模型可知，大悬伸状态下刀具与主轴系统发生较大变形，进而加剧了刀具的偏心跳动。在以悬伸量作为唯一变量的同参数重型铣削实验中最终获得多种复杂表面轮廓，同时复杂的表面形貌在一定条件下又会引起重型铣削再生振动的产生。重型铣削超大切削力激励下的强迫振动为整个铣削过程振动产生的主要形式，而刀齿在断续切削切入与脱离工件时瞬时切削厚度与切削力的突变必然引起铣削过程特定的强迫振动振幅的突变，影响了整个系统的稳定性。加工过程中极易出现过切与欠切的情况，部分刀片瞬时切削厚度过大，最终导致局部刀片的冲击破损与磨损，严重影响已加工表面质量。由于重型铣削振动存在复杂的耦合效应，模型的预测与推理无法真实地反映铣削振动状态，因此有必要对实验加工时采集的振动数据进行分析。

5 重型铣削振动信号分析

重型铣削水室封头实验测得的不同铣削区域x轴向振动信号如图8所示。通过重型铣削振动信号发现时间曲线中冲击特征明显，且随机出现较大加速度幅值。将时域信号进行快速傅里叶变换(fast Fourier transformation 简称FFT)，得到振动信号的FFT实时谱。基频振动出现在频率为79Hz，且基频幅值远高于其他谐频幅值。可见，重型铣削加工过程中超大切削力激励下的强迫振动为重型铣削振动的主要组成部分。虽然重型铣削过程中机构经常发生带有摩擦的自激振动和残余振动等，然而在整个耦合振动中所占比重较小。三组振动信号为铣削加工划分区域的实测数据，三组振动波形的变化规律基本相似。对比三组测试曲线发现，随着刀具与主轴悬伸量的增加，振动信号发生混沌现象越明显，且铣削加速度峰值随之增大。铣削过程中瞬时加速度增大，振动也随之增大，进而破坏重型铣削的平稳性，增大了铣削过程中发生过切和欠切的几率。对应实验所得的已加工表面形貌，不同刀齿瞬时切削轨迹与厚度差异较大，因此瞬时切削力和振动加速度均不相同。

图8 重型铣削振动信号曲线图Fig.8 Heavy milling vibration signal curve graph

结合实验与模型分析结果可知，在大悬伸状态下重型铣削振动直接影响工件的已加工表面形貌、刀具的使用寿命和机床系统的稳定性。针对重型铣削偏心跳动引起的重型铣削振动应采用必要的预防控制措施。结合重型铣削加工的特点，在考虑实际生产加工效率的同时，合理选择加工参数，适当减小轴向切深和进给速度，选用结构刚度大的刀盘与主轴并优化进给系统刚度，同时选用刀齿密度小的刀盘。刀齿密度的减小使同时参与切削的齿数减少，铣削力减小，进而增大了重型铣削的稳定性。同时在加工过程中应尽量避免主轴处于大悬伸量状态，铣削系统应对铣削振动采取主动控制措施，尽可能减小铣削水室封头过程中的重型铣削振动。

6 结 论

1) 分析了加工水室封头重型铣削振动的主要来源，针对重型铣削加工水室封头外球面现场实验得到的已加工表面形貌进行分析，得到了单一参数下悬伸改变量对已加工表面振动波纹分布的影响规律。结果表明，重型铣削过程中刀具与工件间的相互振动是形成已加工表面形貌的主要原因。

2) 通过建立重型铣削刀具偏心跳动模型、刀具与主轴系统变形模型和进给系统刚度模型，结合重型铣削加工特点，建立了考虑刀具偏心跳动的铣削轨迹模型和瞬时铣削厚度模型。获得了考虑重型铣削刀具偏心跳动、刀具与主轴系统轻微变形和进给系统刚度影响下重型铣削微元瞬时切削半径表达式。获得重型铣削瞬时铣削厚度模型，建立以瞬时切削厚度为函数的重型铣削力模型，通过实验数据对刀具偏心跳动模型进行数值计算与验证，分析表明重型铣削振动存在复杂的耦合效应。

3) 通过分析重型铣削实验测得的振动信号，阐述了实际加工过程中重型铣削振动的影响因素及规律，并验证了预测结果的准确性，为进一步研究重型铣削振动冲击特性奠定了基础。

[1] 程耀楠, 刘献礼, 李振加，等. 极端重载切削条件下的刀-屑粘结失效[J]. 机械工程学报, 2012, 48(19): 169-176.

Cheng Yaonan, Liu Xianli, Li Zhenjia, et al. Tool-chip adhering failure under extremely heavy cutting[J]. Journal of Mechanical Engineering，2012，48(19): 169-176.(in Chinese)

[2] 严复钢, 何耿煌, 刘献礼. 极端重载条件下高效切削刀具技术[J]. 哈尔滨理工大学学报, 2011, 16(6): 11-16.

Yan Fugang, He Genghuang, Liu Xianli. Extreme under heavy load and high efficiency cutting tool technology[J]. Journal of Harbin University of Science and Technology, 2011, 16(6): 11-16. (in Chinese)

[3] 江浩, 龙新华, 孟光. 侧铣加工振动与表面轮廓形成[J].上海交通大学学报,2008, 42(5): 730-735.

Jiang Hao, Long Xinhua, Meng Guang. The cutting vibration and surface profile generation in peripheral milling[J]. Journal of Shanghai Jiao Tong University, 2008, 42(5): 730-735. (in Chinese)

[4] Kenkichi I, Keiichi Y, Tetsutaro H. Chatter control in screw thread turning by spindle speed variation[J]. Transactions of the Japan Society of Mechanical Engineers, Part C, 2004, 70(5): 1529-1534.

[5] Rojas J, Liang C. Experimental investigation of active machine tool vibration control[J]. Smart Structures and Materials, Proceedings of SPIE, 1996, 2721: 373-384.

[6] 吴石, 刘献礼, 肖飞. 铣削颤振过程中的振动非线性特征试验[J]. 振动、测试与诊断, 2012, 32(6): 935-940.

Wu Shi, Liu Xianli, Xiao Fei. Experimental study of the nonlinear characteristics of vibration in milling chatter[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(6): 935-940. (in Chinese)

[7] 王保升. 瞬时铣削力模型参数辨识及其试验研究[D]. 镇江：江苏大学, 2011.

[8] 李成锋. 介观尺度铣削力与表面形貌建模及工艺优化研究[D]. 上海：上海交通大学, 2007.

[9] Paris H, Peigne G, Mayer R. Surface shape prediction in high speed milling[J]. International Journal of Machine Tools and Manufacture, 2004, 44: 1567-1576.

[10]李沪曾, Spur G. 机床切削振动仿真计算的结构动力学模型[J]. 同济大学学报, 1995, 23(5): 541-546.

Li Huzeng, Spur G. Structure dynamic model simulation machine cutting vibration[J]. Journal of Tongji University, 1995, 23(5): 541-546. (in Chinese)

[11]李沪曾, 徐炳楠. 机床相对激振试验分析[J]. 振动、测试与诊断, 1998, 18(2):143-148.

Li Huzeng, Xu Bingnan. Experimental analysis on vibration of machine tool[J]. Journal of Vibration, Measurement & Diagnosis, 1998, 18(2): 143-148. (in Chinese)

[12]Masatoshi H, Atsuo T, Ho Y J. Behavior of cutting heat in high speed cutting[J]. Journal of JSPE, 1998, 64(7): 1067-1071.

[13]陈勇, 刘雄伟, 俞铁岳, 等. 再生振动和刀具偏心对立铣加工精度综合影响的研究[J]. 工具技术, 2006, 40(5): 28-32.

Chen Yong, Liu Xiongwei, Yu Tieyue, et al. Research on influences of regenerative vibration and cutter eccentricity on machining accuracy in end milling[J]. Tool Technology, 2006, 40(5): 28-32. (in Chinese)

[14]Chen Hongyu, Du Junyi, Deng Lintao. The comparison and analysis of SA508 series steel used for nuclear reactor pressure vessel forgings[J]. Heavy Castings and Forgings, 2008(1): 1-3.

[15]Takasu S, Masuda M. Influence of study vibration with amplitude upon surface roughness in diamond machining[J]. Annals of the CIRP, 1985, 34(1):463-467.

[16]张军, 唐文彦, 强锡富. 切削振动条件下的表面轮廓仿真分析[J]. 工具技术, 2000, 34(2): 43-47.

Zhang Jun, Tang Wenyan, Qiang Xifu. Simulation analysis of surface profile with cutting vibration[J]. Tool Technology, 2000, 34(2): 43-47. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.04.010

国家自然科学基金资助项目(51205095);黑龙江省教育厅科学技术重点资助项目(12541z006)

2014-07-16；

2014-11-27

TH113

程耀楠，男，1977年9月生，博士、教授、硕士生导师。主要研究方向为重型切削理论与刀具技术、槽型优化技术与难加工材料高效加工技术。曾发表《极端重载切削条件下的刀-屑粘结失效》(《机械工程学报》2012年第48卷第19期)等论文。

E-mail: yaonancheng@163.com