直线超声电机设计、建模和应用的研究进展
姚志远, 李晓牛, 李 响, 耿冉冉, 简 月, 刘 振, 代士超
(南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
◀专家论坛▶
直线超声电机设计、建模和应用的研究进展
姚志远, 李晓牛, 李 响, 耿冉冉, 简 月, 刘 振, 代士超
(南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
直线超声电机作为一种新型作动器,以其独特的结构和驱动原理,在高新技术领域有着广泛的应用。首先,回顾了电机结构设计方面的研究进展,提出了电机的设计理论和方法,阐述了电机结构形式的演化和夹持结构的设计方法;其次,介绍了有关电机理论模型的研究进展,提出了定子机电耦合模型、摩擦接触模型和定/动子冲击模型等;最后,报道了直线超声电机在高精度运动平台、细胞显微操作、微夹持器和绝对重力仪方面的最新应用。
压电作动器; 直线超声电机; 结构设计; 动力学模型
引 言
随着高新技术的发展,精密工程、高精加工、生物技术、纳米技术和航空航天等领域对作动器提出了更高的要求。例如,半导体加工[1]、微纳精密定位装置[2]、扫描探针显微镜[3]不仅要求作动执行机构具有纳米级的定位精度,而且具有毫米级的行程。物理光栅三维扫描仪需要在29 mm×23 mm×3 mm狭小安装空间内调整光栅位置,要求有0.5 μm的定位精度和0.5 m/s以上的速度;而核磁共振装置要求作动器无磁场干扰[4]。
目前,传统电磁电机已无法满足先进作动器的需求。超声电机是一种新型的作动器,利用逆压电效应将电能转换成定子的振动能,再通过摩擦作用将定子的振动能转换成动子的运动能[5],具有结构紧凑、功率体积比大、直接驱动、输出形式灵活、动子惯性小、定位精度高、响应快、断电自锁、可控制性好、无电磁干扰和环境适应性好等优点。
直线超声电机分为行波型和驻波型。Sashida等[6]提出了直梁式和环梁式行波型直线超声电机。该电机利用两个兰杰文振子激发直梁或环形梁产生行波波动,从而驱动动子运动。由于需要整个梁产生行波波动,导致电机功耗大、输出效率低,限制了其应用。最早的驻波电机是楔形电机,利用一个兰杰文振子的纵向振动诱发驱动足处的弯曲运动推动动子运动[7],但是,该电机不能实现双向运动。Vasilijev等将Sashida行波电机的直梁设计成短杆,提出一种“Shaking beam”直线超声电机,提高了电机的输出效率[8]。Kurosawa等[9]直接利用两个兰杰文振子设计电机,提出了V形定子结构的直线超声电机,该电机具有更高的输出效率。除了利用夹心式结构外,Tomikawa等[10]还设计一种利用贴片式板结构的纵向振动和弯曲振动直线超声电机,这类电机更利于小型化。Nanomotion公司已将其商业化[8]。综上所述,直线超声电机利用典型的板、梁、杆结构激发其的固有振动,具有结构简单、多样和振动效率高等优点。
随着直线超声电机技术的发展,人们越来越多地关注理论模型研究和应用研究。理论模型涉及电机运动机理分析、定子结构动力学、结构设计、接触摩擦分析和驱动控制研究等方面。模型研究有助于理解电机运行机理、优化结构设计和改善电机的驱动控制,是超声电机研究的重要内容。
首先,回顾了笔者研究团队电机结构设计的研究,提出了电机的设计理论和方法;其次,介绍了笔者研究团队有关电机理论模型方面的研究进展,阐明了电机的驱动机理、冲击碰撞和机电耦合关系等理论;最后,报道了在高精度运动平台、细胞显微操作、微夹器和重力测量系统方面的应用成果。
1 结构设计与方法
1.1 定子结构设计方法
定子的结构设计包含定子结构形式选择、振动模态选择和压电陶瓷片配置。依据直线超声电机研究的实践,提出以下设计原则。
1.1.1 定子结构简单化的设计原则
从结构形式上讲,定子的结构形式越简单振动效率越高,干扰模态与工作模态频率相隔越大。最简单的定子形式为矩形结构,如图1所示[11]。该电机利用矩形板的纵向振动和弯曲振动,在驱动足处产生椭圆运动,驱动动子运动。它具有结构形式简单和运行效率高的优点。矩形板结构电机利用同频的纵向振动和弯曲振动,在一个结构上同时配置纵向振动陶瓷片和弯曲振动陶瓷片来实现两相振动,一定程度上也增加了结构设计的复杂性。

图1 矩形板结构的直线超声电机Fig.1 Rectangular linear ultrasonic motor
1.1.2 基于两个杆(或板)结构的设计原则
电机利用定子的两相振动产生双向运动,因此设计的定子应具有两相振动模态。由于单个简单结构同时配置两相压电陶瓷片比较困难,因此设计两个杆(或者板)的组合结构,分别在单个杆上配置压电陶瓷片,解决了在一个简单结构上同时配置两相压电陶瓷片的难题。杆结构有明显的振动节点,该振动节点可以作为定子支撑的夹持点,从而解决复杂结构夹持困难的问题。
1.1.3 采用连续变截面杆的设计原则
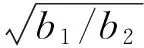
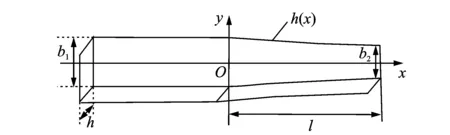
图2 具有连续变截面的兰杰文振子Fig.2 Continuous variable cross-section transducer
1.2 夹持结构设计方法
直线超声电机在振动模态频率附近工作,定子的振动状态决定电机的输出特性。定子的振动状态受定子的结构形式、物理参数和夹持方式的影响。
1.2.1 夹持部件的结构形式
在直线超声电机研究的早期,人们更多地关注定子结构形式的设计,夹持方式没有受到重视。图3为早期的V形直线超声电机及其夹持装置示意图[13]。该电机在底座上设计引导槽,用于固定夹持元件,并通过弹簧沿对称轴方向施加预压力。由于定子的夹持在一条线上,导致定子结构不稳定。为了提高定子结构的稳定性,胡宁等[14]提出将定子的夹持从沿对称轴施加预压力改为沿定子的两侧施加预压力,如图4所示。这样整个定子夹持有3个固定点,定子结构稳定。为了简化结构,又提出了基于柔性铰链代替弹簧施加预压力,设计了两端柔性的夹持元件,如图5所示,它有利于电机小型化。为了增大电机的输出力,姚志远等[15]提出了一端铰支的夹持设计方式,如图6所示。尽管两端夹持方式能够提高电机的输出力,但没有从理论揭示夹持方式对电机输出特性的影响规律。

图3 采用沿对称轴夹持的直线超声电机Fig.3 Linear ultrasonic motor with spring clamping at the axis of symmetry
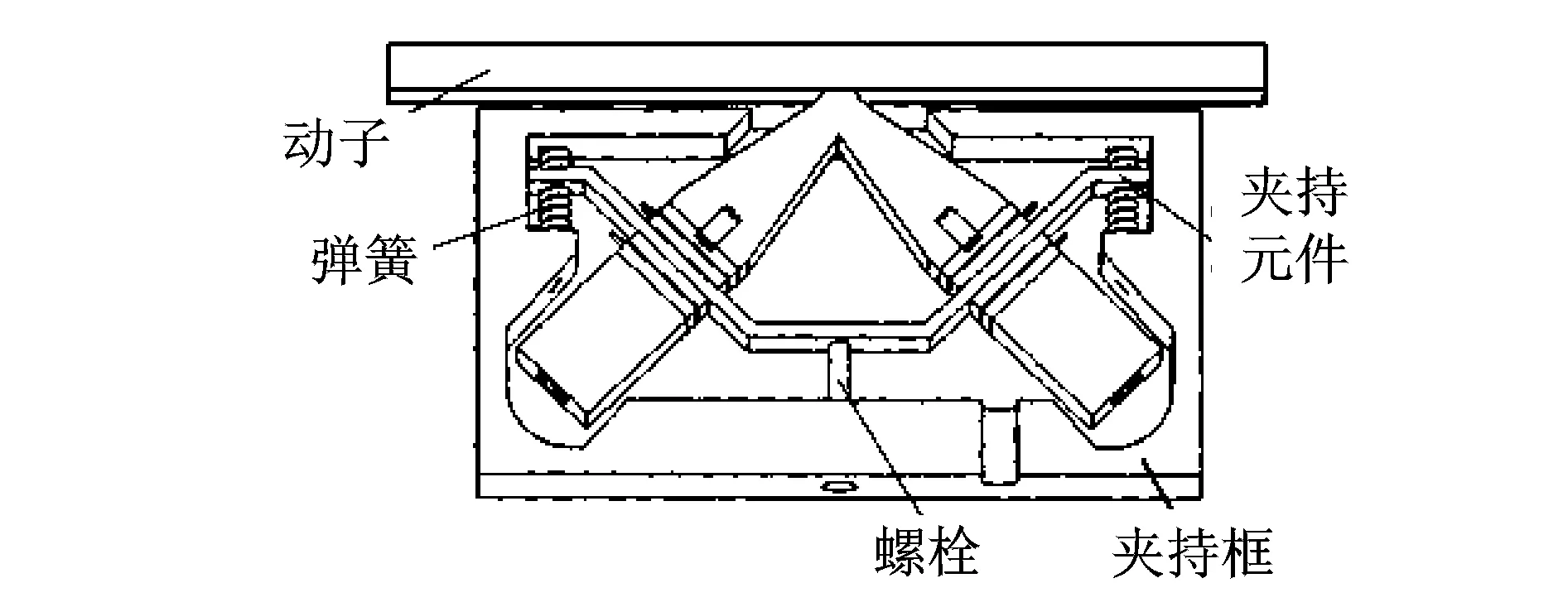
图4 两端弹簧夹持的直线超声电机Fig.4 Linear ultrasonic motor with symmetric spring clamping on both ends

图5 两端柔性夹持的直线超声电机Fig.5 Linear ultrasonic motor with symmetric flexible clamping on both ends

图6 一端铰支的直线超声电机Fig.6 Linear ultrasonic motor with one end hinged
1.2.2 一端铰支的夹持方法
文献[15-16]最早探讨了夹持方式对电机输出特性的影响规律,建立了定子在弹性夹持下的力学模型。模型将夹持简化为法向和切向的两个弹簧,研究弹簧的刚度对切向摩擦力的影响规律,如图7所示。模型分析表明:
1) 提高法向刚度k2有利于增加摩擦力,但当法向刚度k2增加到一定程度时,会抑制定子的振动,导致电机的输出力减少,只有在适当的(法向)预压力范围之内,定子才能达到良好的振动效果;
2) 摩擦力随着切向刚度k1的增大而增大,因此提高摩擦力有利于增加电机的输出力,同时也能够增加电机结构的稳定性。
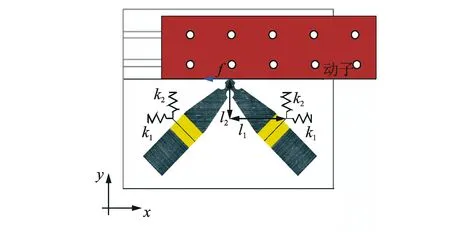
图7 弹簧刚度夹持模型Fig.7 Simplified model of spring stiffness in clamping
图6所示电机采用两端夹持定子的结构。夹持结构的两端分别设计为旋转端和施力端。旋转端通过旋转装置铰支于底座上,确保电机只能转动不能平动;施力端通过预压力施加装置对定/动子施加预压力。建立一端夹持下定子结构的力学模型,模型分析表明:一端铰支式夹持的法向刚度为常数,即为施力弹簧刚度的2倍;而切向刚度与定/动子接触点距施力作用点的垂直距离h成反比,施力作用点与铰支点距离l的平方成正比。因此,一端夹持的直线超声电机通过减小h和增大l能够充分增大切向刚度,提高电机的输出力。
1.3 电机结构形式和驱动方式
通常,超声电机有两相同频的振动模态,在两相模态的振动下,在定子的驱动足处形成椭圆运动,从而驱动动子产生双向运动。设计围绕着两相同频振动模态的定子结构展开。在一个定子结构上设计两相同频振动模态,增加了结构设计的难度。事实上,设计两相模态是为了实现双向运动,如果需要电机一向运动,仅仅需要单一模态,这样电机的结构设计就容易的多。
1.3.1 单模态电机
图8为笔者提出的单模态直线超声电机。该电机的定子为矩形板结构,振动模态采用矩形板的一阶纵向振动或一阶弯曲振动。定子结构如图9所示,由前质量块、压电陶瓷片、夹持元件和后质量块组成。图9中压电陶瓷片有两个分区,称为A相和B相。每个分区的极化方向相同,当A相和B相分别连接信号sin(ω1t)和cos(ω1t)时,定子作弯曲振动,电机向x正方向运动。当A相和B相连接相同的信号sin(ω2t)时,定子作纵向振动,电机向x负方向运动。笔者提出的单模态直线超声电机利用两种不同的模态工作,在设计中无需考虑两种工作模态的相互影响和频率一致性。因此,电机的结构简单稳定,最大推力达到43 N。

图8 矩形结构的单模态直线超声电机Fig.8 Rectangular single-mode linear ultrasonic motor

图9 定子的结构和压电陶瓷片配置Fig.9 Structure of stator and configuration of piezoelectric ceramic
1.3.2 模态解耦电机
单模态电机为了产生双向运动,在一个定子结构上设计了两个模态,这增加了设计的难度。文献[17-18]提出了模态解耦电机,如图10所示。该电机将两个模态设计在不同的振子上,克服了在同一振子上设计两个模态的困难。模态解耦直线超声电机有两个振子,分别称为A振子和B振子。A振子为矩形结构,利用了结构的一阶纵振。B振子也为矩形结构,利用结构的二阶纵振,两向振动的振动频率相同。在空间上两向振子的振动方向垂直,在时间上两相输入信号相差90°的正弦信号。电机通过改变两相输入信号的相位实现双向运动。该电机设计简单,控制性能好,最大推力达到47 N,但两个振子增加了电机的结构复杂性。另外,电机的行程在振子的宽度范围内,受振子A的结构尺寸限制。

图10 模态解耦直线超声电机Fig.10 Linear ultrasonic motor with independent mode
1.3.3 模态耦合电机
尽管模态解耦直线超声电机的振子具有相互独立的两向振动模态,但由于其运动行程短、结构复杂等因素,限制了其使用。图6为60 LumV直线超声电机,该电机有两个振子,每个振子采用连续变截面的收缩结构,如图2所示。两个振子相互垂直,一端相互连接,形成驱动足。为了减小相互间耦合作用,在连接处采用柔性铰链结构。每个振子具有相同频率的一阶纵振和二阶弯振,在一阶纵振的节点处配置纵振压电陶瓷片,以激发振子的纵向振动。由于两个振子的相互耦合作用,同时激发其弯曲振动。
电机的夹持点在振子的一阶纵振节点处,采用一端铰支的夹持元件。为了降低夹持对振子弯曲振动的影响,同时降低两个振子间的振动耦合,在夹持元件的中部采用柔性铰链结构。该电机结构稳定、运行效率高、输出力大、运行速度快、最大推力为50 N,最大速度为1.2 m/s。
1.4 小型化设计
小型化对电机的结构形式、夹持和装配方式提出了更高的要求。苏松飞等[19]采用两端柔性铰链的夹持方式设计了40 LumU电机,如图11所示。该电机的特征尺寸为40 mm,推力为9N。焦阳等[20]采用两端柔性铰链的夹持方式设计了23 LumV电机,如图12所示。该电机的特征尺寸为23 mm,推力为5 N。
为了提高小型电机的推力,Yang等[21]设计如图13所示的40 LumV电机,研究两定子的夹角对输出特性的影响。
研究表明,当两定子夹角为90°时,输出特性最佳。通过改进两振子在连接处(驱动足处)的结构,提高定子的振动效率。通过改进定子的结构和夹持方式提高结构的稳定性,增加电机的输出力。该电机的特征尺寸为40 mm,最大空载速度为784 mm/s,最大输出力为14 N,推重为70。

图11 40 LumU直线超声电机Fig.11 40 LumU type linear ultrasonic motor

图12 23 LumV直线超声电机Fig.12 23 LumV type linear ultrasonic motor

图13 40 LumV直线超声电机Fig.13 40 LumV type linear ultrasonic motor
2 理论模型研究
直线超声电机是一个利用压电材料逆压电效应并基于摩擦驱动机理的机电耦合系统,包含丰富的力学问题。
2.1 定子机电耦合模型
定子作为直线超声电机的核心部件,起到将电能转化为机械能(高频振动)的作用,直接关系到电机的输出效率,因此建立定子的机电耦合模型对整机动力学建模有重要意义。考虑到定子形状的多样性,有限元方法是求解定子机电耦合模型的一般方法,但有限元模型结果很难直接用于摩擦接触模型和控制模型。解析法是另一种求解定子机电耦合模型的有效方法,特别适用于简单定子结构形式。2003年,Tsai等[11]建立了Nanomotion公司生产的SP1型复合模态直线超声电机的整机动力学模型。其中,定子被假设为一个铁木辛柯梁,在此基础上推导出定子的振动方程。2016年,笔者等[22]将V形定子结构看成一个耦合梁结构,建立了复杂的定子机电耦合模型,并给出了相应的解析解。利用该模型研究了定子耦合角度和变截面尺寸对机电耦合系数的影响规律,为优化V形定子结构提供了指导。此外,通过理论和试验结合的方法验证了V形定子在激励下,单个梁中存在纵向和横向两种振动。
2.2 摩擦接触模型
直线超声电机的摩擦接触模型描述定、动子之间能量转换过程。它对于建立整机动力学模型,分析和预测电机的输出性能有重要的意义。
Wallaschek[23]将超声电机定/动子的接触分为两类:a. 行波式接触方式(行波超声电机属于此类接触方式);b. 间歇式接触方式(直线超声电机大多属于此类接触方式)。1999年,Moal等[24]在研究驻波直线电机机械能转换机理时,利用电学试验测试了电机的定子和动子的接触过程,成功观测到周期性的间歇式接触特征,从试验角度验证了驻波直线电机定/动子间歇式的接触特征。
笔者通过建立一个摩擦接触模型,研究了一个面内纵弯型直线超声电机定/动子之间的摩擦接触动力学。该模型从定/动子的动力学方程出发,推导出摩擦界面处于黏着状态时的静摩擦力表达式,利用开关模型仿真出stick-slip运动[25]。同时,采用一个随着驱动足法向振幅增加而递减的动态摩擦因数描述超声减磨效应。图14为stick-slip运动时,一个振动周期内(P1~P5)定/动子之间力的传导过程。在P1段,由于驱动足和动子的切向相对速度为正,故定子对动子产生驱动力,此时界面的摩擦为滑动摩擦。在P2段,由于此时段相对速度为零,故定、动子处于黏着阶段,此时界面的摩擦为静摩擦,由于摩擦力为负,从而定子对动子产生阻碍力。在P3和P5段,由于相对速度为负,故定子对动子产生阻碍力,此时界面的摩擦为滑动摩擦。在P4段,由于此时段的法向压力为零,定/动子处于脱离状态界面的摩擦力为零,动子依靠惯性运动。研究表明,摩擦界面的stick-slip运动更容易在较低电压和较大预压力的情况下出现。当电压低至一定值时,摩擦界面将一直处于黏着状态,这可能是导致低电压死区现象的物理原因,同时还指出超声振动产生的减磨效应会削弱摩擦界面的stick-slip运动。
周胜利等[26]基于概率统计的方法,利用Hertz接触理论研究了一个V形直线超声电机的定/动子接触力学问题。研究表明,在一定范围内定子驱动足的变形量随预压力的增大呈线性关系,当预压力超过一定值时,驱动足的变形量与预压力之间呈现出明显的非线性关系,如图15所示。

图14 界面摩擦力和切向相对速度的时域响应图Fig.14 The time-domain responses of the interface friction and tangential relative velocity
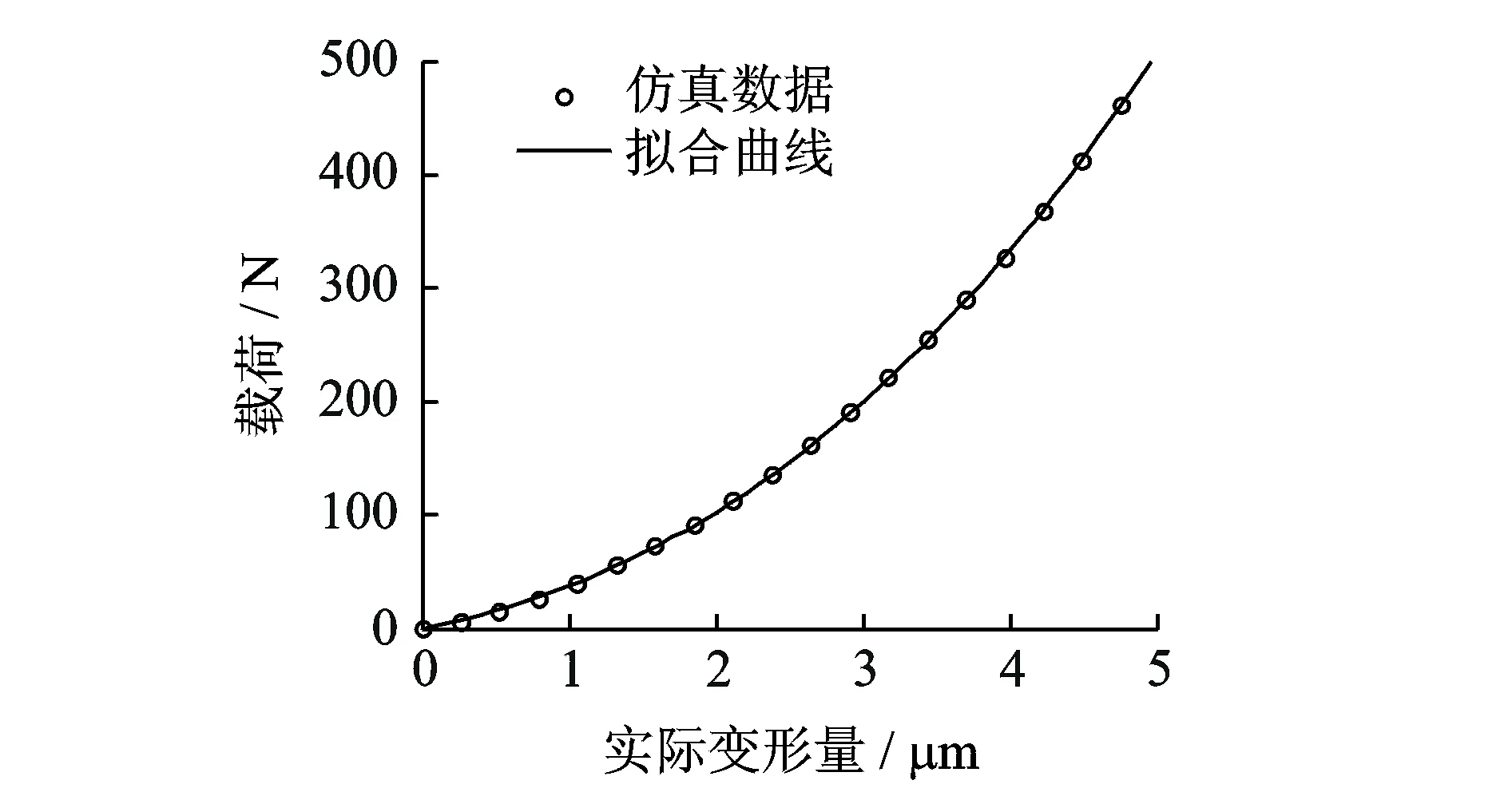
图15 定子驱动足变形量与预压力的关系Fig.15 Relationship between the deformation of the driving tip and preload
2.3 定/动子冲击模型
间歇式接触方式会使直线超声电机定/动子之间的接触表现出明显的冲击特性,这可能会造成定子质心的颤动和一些复杂的冲击动力学行为。Li等[27]基于刚性碰撞的假设,利用经典的恢复系数法研究了硬摩擦材料的定/动子之间的冲击问题,并考虑了由于定/动子的冲击造成的定子质心振动问题。分析表明,定子质心的振动幅值和驱动足由于压电激励产生的振动幅值相当,但前者振动的频率却远低于后者振动的频率。此外,还利用数值模拟的方法研究了由于刚性碰撞产生的法向黏着运动,指出造成这种复杂的非线性动力学行为的原因是由于定子中波的传播受到几何约束的限制以及定子质心振动的叠加,如图16所示[27]。

图16 定/动子冲击造成的驱动足处的黏着运动图Fig.16 Figure of sticking motion at the driving foot caused by impact between the stator and mover
电机的动力学建模还需要进一步完善,主要有以下几点:a.建立考虑摩擦界面粗糙度和高频振动的微观接触模型,以更真实地反映定/动子的接触情况;b.引入动态摩擦模型来替代库伦摩擦模型(静态摩擦模型), 由于定/动子的间歇式接触方式,一些现有的动态摩擦模型(如Dahl模型和LuGre模型)无法直接使用;c.在建模的过程中考虑更多的非线性因素,如压电材料的非线性、定子温度升高引起的共振频率飘移等非线性因素。
3 应用研究
3.1 直线运动平台
笔者开发研制了60 LumV型单自由度直线运动平台[28-30],如图17所示。该平台由定子、夹持件、预压力调节件、滑台和底座组成。该平台经上海市计量测试技术研究院检测,其移动步距在50 nm之内。经中国计量科学研究院检测,采用光栅位移传感器进行闭环定位控制,定位精度为0.36 μm。另外,笔者还开发了两自由度运动平台。

图17 单自由度运动平台Fig.17 High-precision motion platform
3.2 细胞显微操作手
笔者研制了用于细胞穿刺的显微操作手。图18为微操作手的结构图,它由3个直线超声电机平台叠加构成,可沿x,y,z方向运动。其中:y轴平台直接固定在x轴平台上;z轴平台斜向45°固定在连接钢块上,再叠加在y轴平台之上;x,y方向的运动行程为80 mm;z方向的运动行程为30 mm。安装有探针的末端器固定在z轴平台的滑块上,方向与z轴平行。整个微操作手尺寸为128 mm×178 mm×100 mm。微操作手的最大运行速度为360 mm/s,三个自由度上的位移分辨率均为50 nm以内,能很好地满足细胞穿刺的要求,如图19所示。

图18 细胞穿刺试验系统Fig.18 Cell perforation system

图19 单细胞穿刺Fig.19 Single cell perforating image
3.3 空间并联微夹持器
微夹持器利用两手指对微小物体进行抓取、移动和翻转等操作,在生物技术领域有广泛应用。微夹持器需满足重量轻、体积小、驱动力大、精度高和行程大等要求。现有的微夹持器主要利用压电陶瓷管的静变形作为驱动元件。该类型微夹持器具有纳米级的控制精度,但运动行程小(微米级)。随着科技发展,微夹持器除了要求高精度和分辨率外,还希望实现更大范围的操作。若采用基于直线超声电机作为驱动元件,可显著增大微夹持器的操作范围,极大提高微夹持器的适用范围。文献[31-32]提出了基于直线超声电机的空间并联微夹持器。
图20为微夹持器的结构图,它由直线超声电机、导轨、基座、固定臂、柔性铰链、支撑圆盘和活动臂组成。该微夹持器采用空间并联双层结构,下层为基层,由固定臂和主体基座构成,基层相对地面静止,固定臂在操作过程中始终处于静止状态,而主体基座用于构成整体框架。上层为运动层,由活动臂和支撑圆盘构成,活动臂用于抓取和翻转微小物体,支撑圆盘承受来自3个超声电机的驱动运动,使之转化为活动臂的运动。3个直线超声电机均匀分布在微夹持器主体基座上,其输出力垂直于上下两层结构,通过导轨及铰链与运动层连接,驱动运动层运动,使活动臂产生需要的运动。

图20 微夹持器的结构图Fig.20 Structure diagram of micro gripper
在高倍光学显微镜下,通过单步位移输出的方式可以大致描绘出探针针尖的轨迹曲线,试验结果如图21所示。在显微镜下抓取半径为250μm的钢珠影像如图22所示。相对于串联机构,并联机构具有运动惯量低、负载能力强、刚度大和无累积误差等优点,因此选用并联机构可提高微夹持器的稳定性及精度。

图21 工作轨迹及最大工作范围Fig.21 Movement locus and maximum operating space
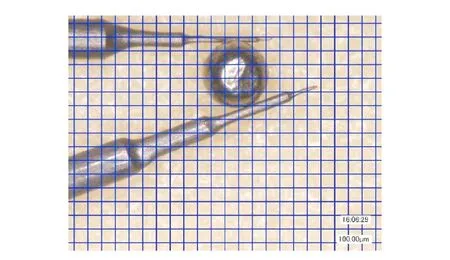
图22 半径为250 μm钢珠抓取试验Fig.22 Steel balls gripping with radius of 250 μm
3.4 绝对重力仪
自由落体式绝对重力仪通过落体在真空中运动的时间和距离来确定重力值大小。其中,自由落体装置用于实现稳定的、可重复的自由落体运动,是绝对重力仪的核心组成部件。传统的自由落体装置通常采用电磁电机作为驱动元件。由于电磁电机不能直接输出需要的直线运动,必须增加机械传动装置,且其本身的复杂结构,使整体系统繁复沉重,不便于携带。采用直线超声电机[16]替代电磁电机作为驱动元件,可有效避免复杂传动机构,使结构更加简洁轻便,可直接在真空腔内运行,如图23所示。
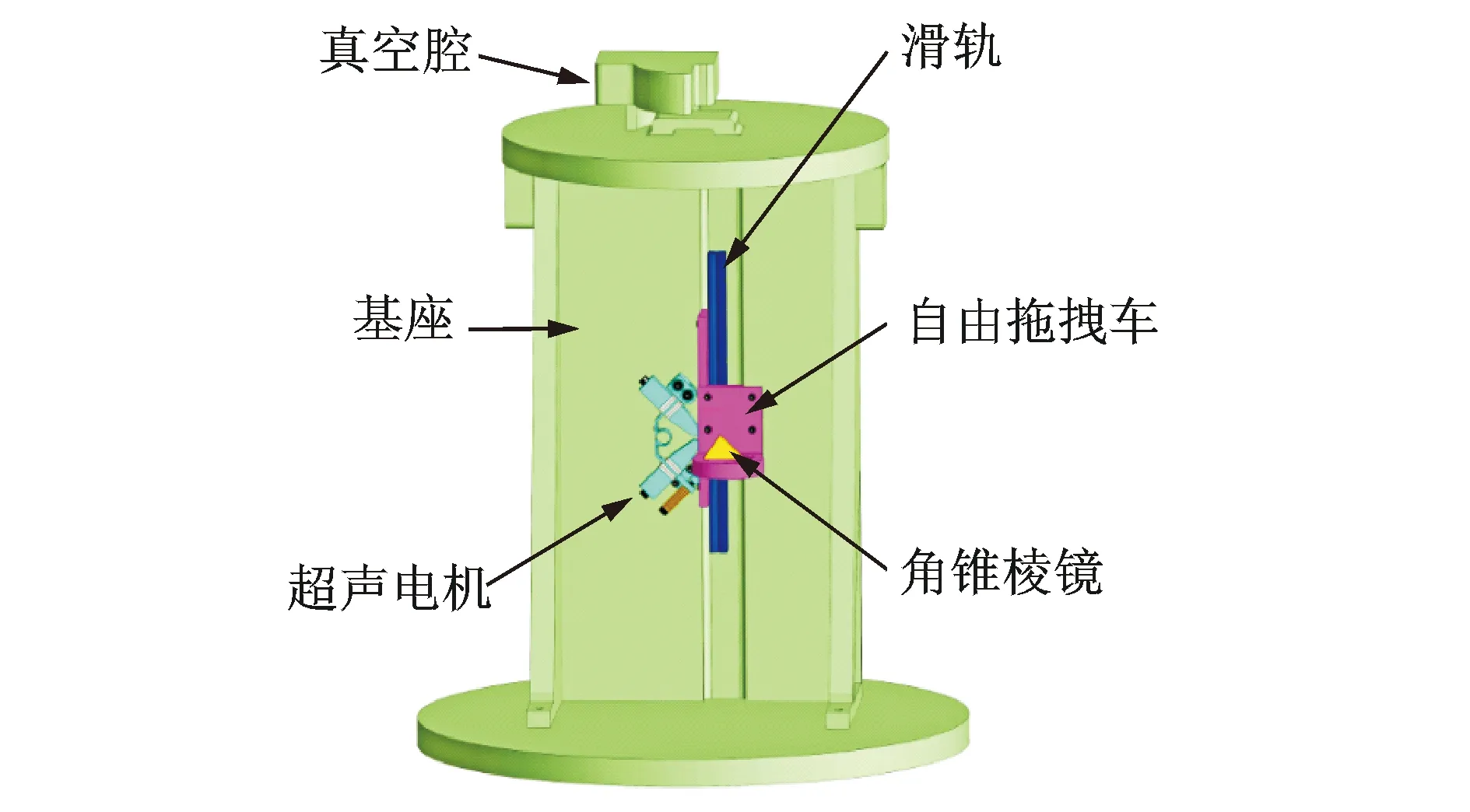
图23 基于超声电机的绝对重力仪Fig.23 Absolute gravimeter based on ultrasonic motor
4 结束语
笔者团队提出了采用连续变截面杆设计定子的方法和柔性夹持方法,提高了电机的结构稳定性和输出效率。设计了模态解耦型电机和单模态电机,避免了模态耦合型电机两相频率不一致的问题,使电机结构设计更加容易。采用解析方法建立了复杂定子的机电耦合模型。提出了纵弯模态耦合型电机的摩擦接触模型,并阐明了其驱动机理。建立了定动子冲击模型,刻画了定动子间的力学行为。研制了60 LumV运动平台,其最大输出力为50 N,最大速度为1.2 m/s,最小步距为50 nm,定位精度达到0.36 μm。研制了细胞显微操作手,实现了单细胞穿刺。研制了空间并联微夹持器,实现了250 μm颗粒的抓取。
随着超声电机技术的发展,直线超声电机研究向着寻求更高的运行效率、结构稳定性、速度稳定性、运行稳定性和控制精度方向发展。它的研究更加关注动力学建模、能量输送、转换机理和寿命与可靠性分析。直线超声电机的研究向小型化方向发展,通过设计方法的突破,摆脱制造技术的限制对加工装配的影响,研制更加微小的直线超声电机。随着超声电机的技术进步,直线超声电机将在精密工程、高精加工、生物技术、纳米技术和航空航天等领域得到更广泛的应用。
[1] Tan K K, Lee T H, Huang S. Precision motion control:design and implementation[M]. Berlin:Springer Science & Business Media, 2007:1-2.
[2] Xu Q. Design and implementation of a novel rotary micropositioning system driven by linear voice coil motor[J]. Review of Scientific Instruments, 2013,84(5):550011-550018.
[3] Bazaei A, Yong Y K, Moheimani S R. High-speed Lissajous-scan atomic force microscopy:scan pattern planning and control design issues[J]. Review of Scientific Instruments, 2012,83(6):637011-6370110.
[4] Esser C M, Parthiban C, Zinn M R. Development of a parallel actuation approach for MR-compatible robotics[J]. Mechatronics, IEEE/ASME Transactions on, 2014,19(3):904-915.
[5] 赵淳生. 超声电机技术与应用[M]. 北京:科学出版社,2007:1-2.
[6] Sashida T, Kenjō T. An introduction to ultrasonic motors[M]. Oxford:Oxford University Press, Incorporated, 1993:1-4.
[7] Vasiliev P, Klimavichjus R, Kondratiev A, et al. Vibration motor control:UK,2020857[P].1979-11-21.
[8]Hemsel T, Mracek M, Twiefel J, et al. Piezoelectric linear motor concepts based on coupling of longitudinal vibrations[J]. Ultrasonics, 2006,44:591-596.
[9] Kurosawa M, Kodaira O, Tsuchitoi Y, et al. Transducer for high speed and large thrust ultrasonic linear motor using two sandwich-type vibrators[J]. IEEE Transactions on Ultrasonic, Ferroelectrics, and Frequency Control, 1998,45(5):1186-1195.
[10]Tomikawa Y, Ogasawara T, Takano A. Ultrasonic motors-constructions/characteristics/applications[J]. Ferroelectrics, 1989,91(1):163-178.
[11]Tsai M S, Lee C H, Hwang S H. Dynamic modeling and analysis of a bimodal ultrasonic motor[J]. IEEE Transactions on Ultrasonic, Ferroelectrics, and Frequency Control, 2003,50(3):245-256.
[12]姚志远, 杨东, 赵淳生. 杆结构直线超声电机的结构设计和功率流分析[J]. 中国电机工程学报, 2009,29(24):56-60.
Yao Zhiyuan, Yang Dong, Zhao Chunsheng. Structure design and power flow analysis of bar-structure linear ultrasonic motors[J]. Proceedings of the CSEE, 2009,29(24):56-60. (in Chinese)
[13]杨东.双变幅杆 V 形直线超声电机研究[D]. 南京:南京航空航天大学, 2009.
[14]胡宁,姚志远,赵文涛. 直线超声电机柔性夹持元件的设计[J]. 中国机械工程, 2012, 23(9):1089-1091.
Hu Ning, Yao Zhiyuan, Zhao Wentao. Design of clamping components for a linear ultrasonic motor[J]. China Mechanical Engineering, 2012,23(9):1089-1091. (in Chinese)
[15]姚志远, 刘振, 简月.一端铰支的直线超声电机的夹持定位装置:中国,201410166165.6[P]. 2014-07-23.
[16]简月, 姚志远, 杨模尖, 等. V 型直线超声电机梁式夹持的结构设计[J]. 光学精密工程, 2015,23(5):1358-1364.
Jian Yue, Yao Zhiyuan, Yang Mojian, et al. Structure design of beam type clamp for V-shape ultrasonic motor[J]. Optics and Precision Engineering, 2015,23(5):1358-1364. (in Chinese)
[17]周胜利. 双振子驻波直线超声电机的设计与建模[D]. 南京:南京航空航天大学, 2014.
[18]Zhou Shengli, Yao Zhiyuan. Design and optimization of a modal-independent linear ultrasonic motor[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2014,61(3):535-546.
[19]苏松飞,姚志远,耿冉冉,等. U形直线超声电机结构设计[J]. 哈尔滨工程大学学报, 2012,33(6):759-763.
Su Songfei, Yao Zhiyuan, Geng Ranran, et al. Structure design of a linear ultrasonic motor with a U-shaped vibrator[J]. Journal of Harbin Engineering University, 2012,33(6):759-763. (in Chinese)
[20]焦阳, 姚志远, 胡正旭. U型直线超声波电动机的小型化结构设计[C]∥第十六届中国小电机技术研讨会论文摘要集. 上海:微特电机,2011:207-212.
[21]Yang Mojian, Yao Zhiyuan, Li Xiang. Structure design of hinged beam type clamp for miniature linear ultrasonic motor[C]∥Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA). Jinan: IEEE, 2015:309-312.
[22]Li Xiaoniu, Yao Zhiyuan. Analytical modeling and experimental validation of a V-shape piezoelectric ultrasonic transducer[J]. Smart Materials and Structures, 2016 (25):075026.
[23]Wallaschek J. Contact mechanics of piezoelectric ultrasonic motors[J]. Smart Materials and Structures, 1998 (7):369-381.
[24]Moal P L, Joseph E, Ferniot J C. Mechanical energy transductions in standing wave ultrasonic motors:analytical modeling and experimental investigations[J]. European Journal of Mechanics, A/Solids, 2000 (19):849-871.
[25]Li Xiang, Yao Zhiyuan, Wu Ranchao. Modeling and analysis of stick-slip motion in a linear piezoelectric ultrasonic motor considering ultrasonic oscillation effect[J]. International Journal of Mechanical Sciences, 2016 (107):215-224.
[26]周胜利,姚志远. 直线超声电机定/动子接触的微观力学模型[J]. 振动与冲击,2012 (31):90-93.
Zhou Shengli, Yao Zhiyuan. Micromechanic model for contact between a linear ultrasonic motor′s stator and mover[J]. Journal of Vibration and Shock, 2012 (31):90-93. (in Chinese)
[27]Li Xiang, Yao Zhiyuan, Wu Ranchao. Modeling and sticking motion analysis of a vibro-impact system in linear ultrasonic motors[J]. International Journal of Mechanical Sciences, 2015 (100):23-31.
[28]葛兆凤. 压电运动平台精密定位控制方法研究[D]. 南京:南京航空航天大学,2012.
[29]葛兆凤, 姚志远, 赵雷. 超声波电动机驱动的三维精密平台定位系统∥第十六届中国小电机技术研讨会论文摘要集. 上海:微特电机,2011:30-33.
[30]Xu Zhaoli, Yao Zhiyuan. Research on control methods of speed stability by AR model based on linear ultrasonic motor[C]∥Applied Mechanics and Materials. Switzerland:Trans Tech Publications, 2013:777-780.
[31]Geng Ranran, Yao Zhiyuan, Mills J K. LUM-driven micromanipulator for cell wall perforation[J]. International Journal of Mechatronics and Automation, 2015,5(2/3):86-91.
[32]王赟,姚志远,耿冉冉. 直线超声电机驱动的并联微操作手的结构设计[J]. 机器人,2015,37(5):573-580.
Wang Yun, Yao Zhiyuan, Geng Ranran. Structure desing of a parallel micromanipulator driven by linear ultrasonic motors[J]. Robot, 2015,37(5):573-580. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.04.001
国家重点基础研究发展计划(“九七三”计划)资助项目 (2011CB707602);国家重大仪器设备开发专项资助项目(2012YQ100225);国家自然科学基金资助项目(50975136, 51275229); 江苏高校优势学科建设工程资助项目(PAPD)
2016-05-05
TH133; TM356
姚志远,男,1961年6月生,教授、博士生导师。现为中国航空学会会员、全国高校机械工程测试技术研究会常务理事、中国振动工程学会动态测试专业委会常务委员、《振动、测试与诊断》常务编委、副主编。主要研究方向为结构振动特性分析和动力学建模。研究涉及车辆的振动、噪声估计和控制;基于环境振动的大型结构模态识别和损伤识别;超声电机的结构动力学分析、动力学建模、接触摩擦机理以及结构设计。发表论文50余篇,获国家发明专利10余项,荣获国家技术发明二等奖1项。E-mail:zyyao@nuaa.edu.cn

