基于动态数据挖掘的热力参数传感器故障诊断

李 蔚， 俞芸萝， 盛德仁， 陈坚红

(浙江大学热工与动力系统研究所 杭州，310027)



基于动态数据挖掘的热力参数传感器故障诊断

李 蔚， 俞芸萝， 盛德仁， 陈坚红

(浙江大学热工与动力系统研究所 杭州，310027)

针对火电机组热力参数动态数据的海量、高维特点，提出了一种基于动态数据挖掘的热力参数传感器故障诊断新方法。该方法通过对热力参数信号进行经验模态分解，获得一系列平稳的本征模态函数(intrinsic mode function,简称IMF)分量和一个趋势余量，实现传感器故障特征信息的动态挖掘。以各IMF分量和趋势余量的方差作为特征向量构建欧氏距离判别函数，结合径向基函数神经网络确认传感器是否发生故障。根据专家经验得到的规则分析传感器测量值与理论值之间的差值，判别传感器的故障类型。以某电厂600MW火电机组实时运行数据为基础进行仿真实验，结果表明：该方法能够仅使用热力参数传感器正常状态下的样本，有效区分传感器故障造成的信号变化与机组本身正常负荷波动造成的信号变化，实现快速准确地对热力参数传感器的工作状态和故障类型进行判别。

热力参数传感器； 动态数据挖掘； 经验模态分解； 径向基神经网络； 故障诊断

引 言

火电机组热力系统中传感器的工作环境恶劣，热力参数传感器易出现各种故障，影响火电厂机组的安全经济运行。如何通过分析热力参数传感器数据，对热力参数传感器进行故障检测和判别，甚至计算故障替代值，对火电厂进行运行控制、降低运行成本和减少安全事故具有重要意义。

火电机组热力参数传感器数据是一种典型的随时间变化的动态非线性数据，具有海量、高维、非平稳和非线性的特点。传统的数据挖掘技术很难有效地对这类数据进行分析，因此动态数据挖掘技术应运而生。动态数据挖掘通常以动态数据库和实时数据库为数据的主要来源，数据处理是动态数据挖掘的核心部分[1-3]。传统的数据处理方法包括傅里叶变换和小波变换等。傅里叶变换能有效分析平稳数据，但热力参数传感器数据往往表现为非平稳特征，傅里叶变换不能同时兼顾热力参数传感器数据在时域和频域中的全貌和局部化特征，而这些局部化特征正是热力参数传感器故障的表现[4]。小波变换[5]能同时获得数据的时域和频域的局部化信息，但小波基函数的长度有限，作小波变换时会产生能量泄漏，很难对数据在时域和频域作精确分析。另一方面，小波变换需预先选择小波基和分解尺度，且所得结果为与数据本身无关的某一固定频段的数据，因此小波变换不具有自适应性[6]。

Huang等[7]提出了经验模态分解(empirical mode decomposition，简称EMD)算法，在时间序列上具有较好的分解效果，并在很多领域得到了应用。钟佑明等[8]应用EMD对在线信号进行动态、连续和高精度处理。樊奕辰等[9]分别应用Savitzky-Golay平滑、移动窗口平滑以及EMD方法对原始光谱进行去噪处理，结果表明，经EMD处理后的模型预测效果最优。孙洁娣等[10]应用泄漏信号欠定盲分离方法对传感器采集的混合信号进行EMD分解，实现泄漏信号的有效提取。文献[11]基于EMD提出估计沸水反应堆不稳定相关系数的方法，并用福斯马克稳定性基准报告的两个案例进行了验证。文献[12]提出一种基于混合搭配探测器和EMD的轴承故障诊断方法，该方法与轴承的负荷情况无关。文献[13]将EMD应用于存在诸多非线性和非平稳领域的海洋环境，研究了温度、溶解氧与时间序列的内在相关性。文献[14]基于EMD和核心向量回归信号分析技术，提出了大型配电系统的智能故障定位方法，其训练时间和内存比现有的其他算法更少。

笔者提出一种基于动态数据挖掘的热力参数传感器故障诊断方法。首先，通过对传感器数据进行EMD分解，获得一系列平稳的本征模函数分量和一个趋势余量，实现传感器故障特征信息的动态挖掘；然后，以各IMF分量和趋势余量的方差作为特征向量构建欧氏距离判别函数，检测出非正常的传感器数据，并通过径向基函数 (radical basis function,简称RBF)神经网络确认传感器是否发生故障；最后，以专家经验得到的规则分析传感器测量值与理论值间的差值，判别传感器的故障类型。该方法能够有效区分热力参数传感器故障造成的信号变化与热力系统本身正常波动造成的信号变化。另外，该方法在训练RBF神经网络时只需要热力参数传感器正常状态下的样本，克服了热力参数传感器故障样本稀少的困难。在热力参数传感器发生故障情况下，该方法可以计算出理论值代替故障值，实现热力系统的容错控制。

1 基本原理

1.1 动态数据挖掘

EMD方法认为任何复杂的时间信号都是由一些相互不同、简单的、非正弦函数的IMF分量组成。EMD方法的基本思想是：假如一个原始数据序列X(t)的极大值或极小值数目比上跨零点(或下跨零点)的数目多2个(或2个以上)，或者上、下包络线的均值不是处处为零，则该数据序列就需要进行平稳化处理[7]。具体处理方法见文献[15-16]。经过EMD分解后，原始信号x(t)可表示为n个IMF和残余rn(t)之和

(1)

IMF分量反映了原始信号的特征尺度，代表着非线性非平稳数据序列的本征模态特征，通过分析IMF分量的特征，便可推知原数据序列特征信息。

1.2 RBF神经网络

笔者使用RBF神经网络确认传感器是否发生故障。RBF神经网络为一种三层的前向网络。第1层为输入层，由信号源节点组成；第2层为隐藏层，其节点数由描述问题的需要而定，隐藏层中神经元的变换函数即为径向基函数，是对中心点径向对称且衰减的非负非线性函数；第3层为对输入模式做出响应的输出层。

RBF神经网络结构简单、训练简洁，且学习收敛速度快，能够逼近任意非线性函数，被广泛应用于时间序列分析和模式识别等领域[17-19]。

2 故障诊断方法

2.1 动态数据特征挖掘

基于EMD的动态数据特征挖掘计算步骤如下。

1) 对待检测传感器的数据样本进行EMD分解，每组数据样本各得到若干个IMF分量和一个趋势余量，不同数据样本所得的IMF分量的个数不等。设其中的最大值为m，若某个样本的IMF个数少于m，则补充零向量使其具有m个分量C1(t),C2(t),…,Cm(t)。

2) 求每组数据样本所得IMF分量Ci(t) 的方差Di及趋势余量rn(t)的方差Dn

其中：L为样本长度，即每组数据样本所包含的数据总数。

3) 以方差为元素，根据式(2)和式(3)构建该组数据样本的特征向量

(4)

2.2 故障检测与判别

基于动态数据挖掘的热力参数传感器故障检测与判别方法包括以下步骤。

1) 在传感器正常运行状态下，按时间间隔Δt和样本长度L对待诊断传感器及N-1个与其相关联的传感器进行P次采样，共得到N×P组传感器正常运行数据样本。

2) 分别求P个待检测传感器样本的Di(i=1,2,…,m)和Dn的平均值Dk0,i(i=1,2,…,m)，Dk0,n。将Dk0,i和Dk0,n作为待检测传感器的模板特征向量Tk0

(5)

3) 按时间间隔Δt和样本长度L 采集待诊断传感器数据，计算待诊断传感器数据的特征向量Tk与模板特征向量Tk0间的欧氏距离dk,k0

(6)

其中：Dk,i为传感器待诊断数据第i个IMF分量的方差；当i=n时，Dk,n为趋势余量的方差。

4) 当dk,k0大于或等于阈值λ1时，认为待检测传感器可能出现故障。将P组待检测传感器数据样本作为输入数据，其余N-1个关联传感器的P组数据样本作为输出数据，建立RBF神经网络模型，求出待检测传感器在正常状态下的数据理论值。

5) 计算与传感器测量数据的差值Δyc,r，若大于或等于阈值λ2，则确定待检测传感器发生故障。

6) 利用专家经验规则对传感器测量值及差值Δyc,r的特征分析确定传感器的故障类型。

3 故障诊断实例

基于动态数据挖掘的热力参数传感器故障诊断方法的流程如图1所示。为了验证该故障诊断方法的有效性，针对某火电厂一台600MW火电机组SIS系统实时数据库存储数据的8个测点进行了算例分析，包括主蒸汽温度、锅炉出口主蒸汽温度、高压主汽阀左侧进汽温度、高压主汽阀右侧进汽温度、低压排汽温度、调节级温度、高温再热器出口温度和再热蒸汽温度。其中：主蒸汽温度传感器作为待诊断传感器，其余7个传感器作为关联传感器。

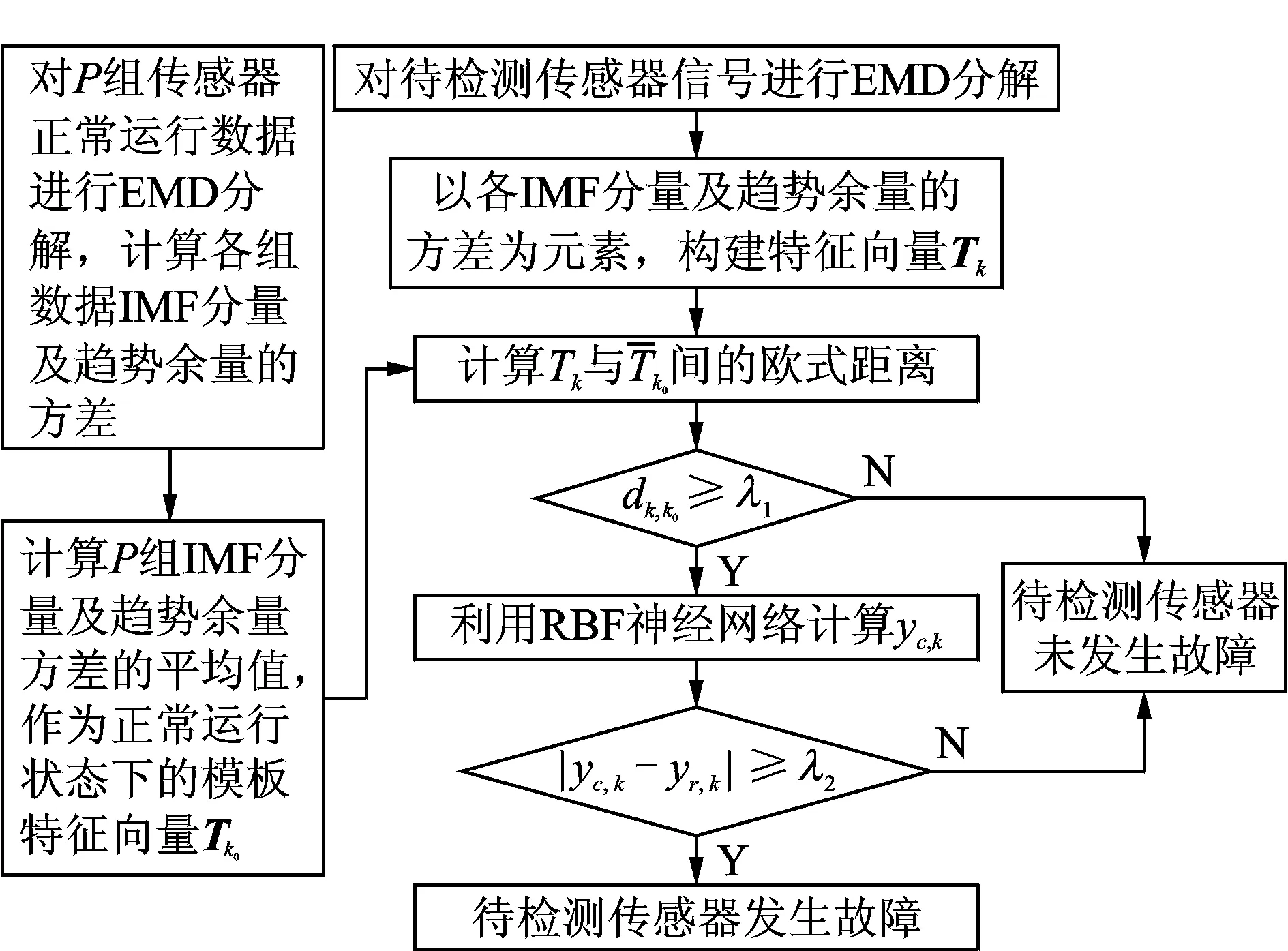
图1 热力参数传感器故障诊断方法流程图Fig.1 Flow chart of thermal parameter sensor fault diagnosis method

在实际运行数据的基础上，依据文献[20]提出的传感器故障仿真模型，对主蒸汽温度传感器的4种典型故障(完全失效故障、精度下降故障、恒定偏差故障和漂移故障)进行仿真。加上正常运行状态，共获得5种状态信号。将样本长度设置为120点。取50组正常运行数据用于计算模板特征向量，取正常运行、完全失效故障、精度下降故障、恒定偏差故障和漂移故障5种状态下各12组数据作为待检测主蒸汽温度数据。

对50组正常运行时的主蒸汽温度数据及60组待检测数据进行EMD分解，提取出每组主蒸汽温度数据的特征向量。以漂移故障为例，主蒸汽温度信号的EMD分解结果如图2所示。由图2可见，EMD方法能够自适应地将非稳态、非线性的主蒸汽温度信号按特征时间尺度从小到大的顺序，依次将各IMF分量分解出来。计算出主蒸汽温度传感器正常运行状态下的模板特征向量后，求出每组待检测主蒸汽温度数据的特征向量与模板特征向量的欧氏距离，其中阈值λ1=0.2(需要说明的是，阈值会影响方法的检测结果，需要根据不同热力参数的特点，反复实验进行确定)。至此，共有50组待检测主蒸汽温度数据初步判断为故障数据。

图2 主蒸汽温度传感器漂移故障信号及其EMD分解结果Fig.2 A drift failure signal of main steam temperature sensor and the EMD decomposed results

由于热力系统本身存在着波动，并且信号可能存在噪声，此时无法区分出是热力系统本身发生了波动还是确实存在热力参数传感器故障，且无法判别何时发生了故障及故障类型，因此需要结合RBF神经网络做进一步诊断。

以50组主蒸汽温度传感器正常运行数据为输出，其他7个传感器的数据为输入，建立RBF神经网络。训练完成后，将与50组故障数据相对应的其他7个传感器数据输入训练完成的RBF神经网络，计算出在正常时主蒸汽温度传感器的理论值ykc。计算ykc与传感器测量值ykr的差值Δyc,r，此时阈值λ2=2。至此，共有48组数据确定为传感器故障，2组数据确定为正常数据，与实际情况完全相符。

主蒸汽温度传感器的4种故障数据、差值及计算出的理论值如图3～6所示。可以看出，该方法对于这4类故障都能给出合理的模拟信号来代替出现故障的传感器信号。此外，不同故障类型对应的差值Δyc,r呈现出不同的特征。可通过对传感器测量值和差值Δyc,r的特征分析，利用专家经验规则来确定传感器的故障类型。

1) 如果传感器测量值ykr保持不变 (如图3(a)所示)，则判定传感器发生完全失效故障。

2) 如果传感器测量值并未保持不变，而差值Δyc,r时正时负，且平均值趋于零(如图4(a)，(b)所示)，则判定传感器发生精度下降故障。

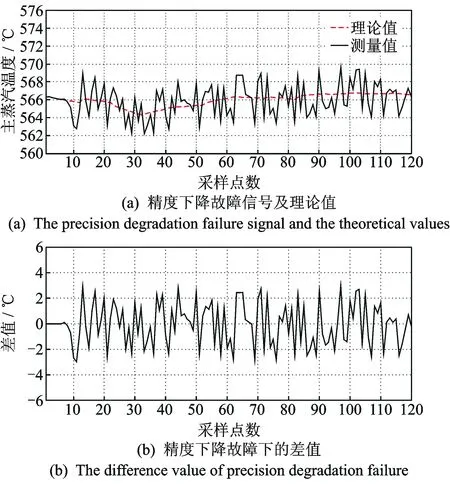
图4 精度下降故障诊断Fig.4 The fault diagnosis of precision degradation failure

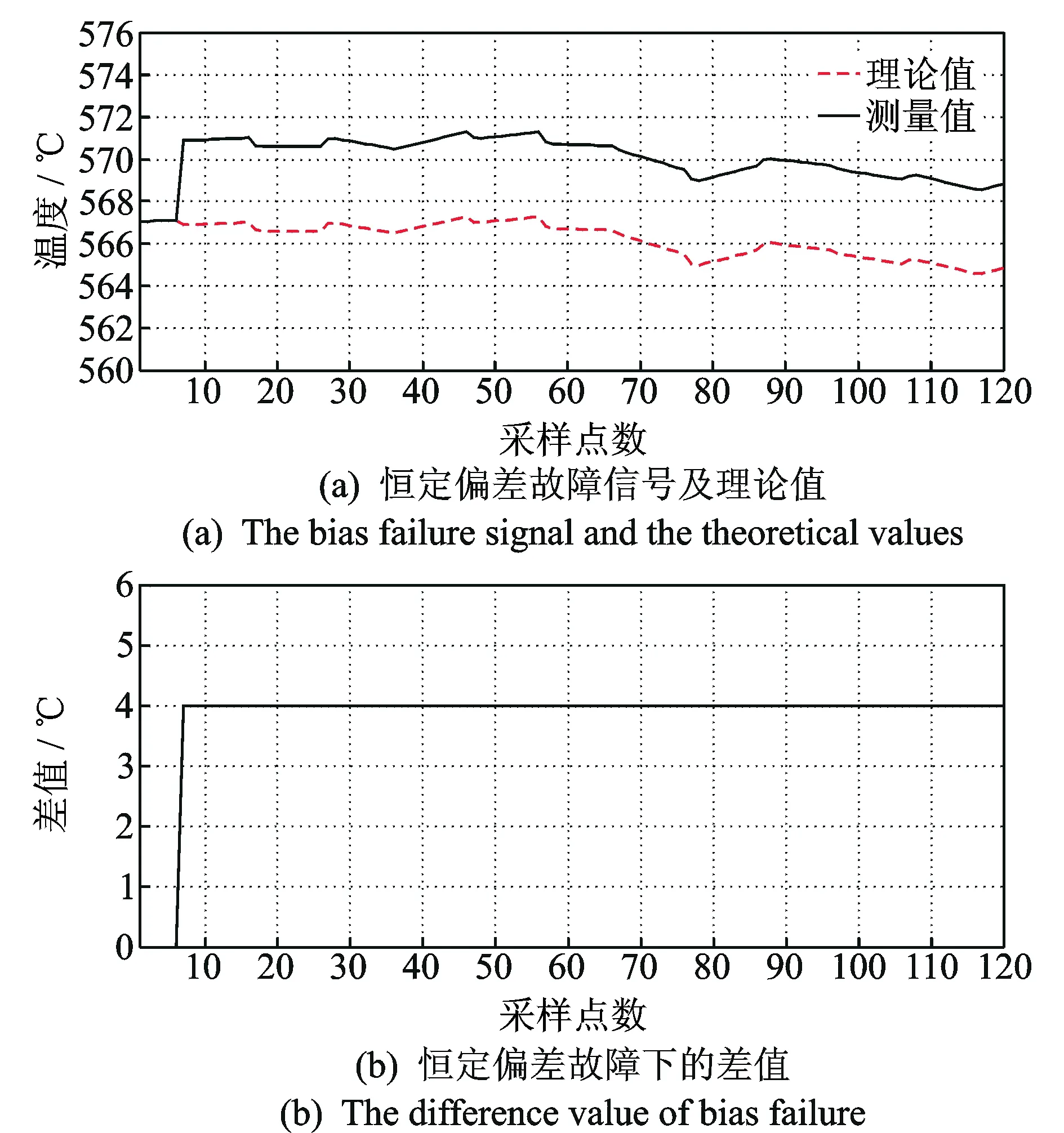
图5 恒定偏差故障诊断Fig.5 The fault diagnosis of bias failure

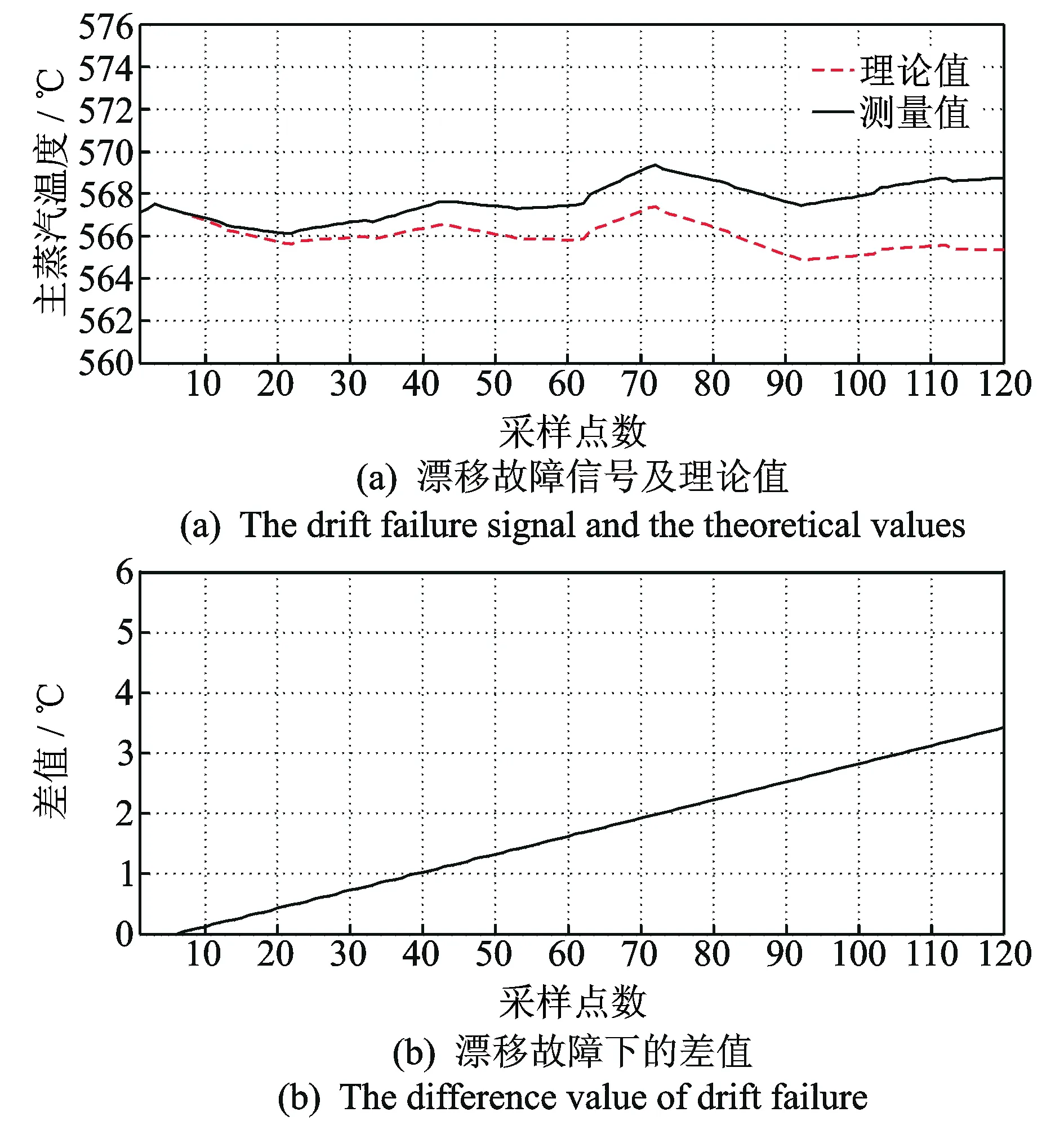
图6 漂移故障诊断Fig.6 The fault diagnosis of drift failure

3) 如果传感器测量值并未保持不变，而差值Δyc,r为某一恒定常数(如图5(b)所示)，则判定传感器发生恒定偏差故障。

4) 如果传感器测量值并未保持不变，而差值Δyc,r随时间发生线性变化(如图6(b)所示)，则判定传感器发生漂移故障。

按照以上方法，48组传感器故障数据均被正确识别。结果表明，该方法可以准确诊断出传感器的工作状态，并区分出4种传感器典型故障，从而验证了该方法的有效性。

4 结 论

1) 该方法能够快速准确地检测热力参数传感器故障，并对故障类型和发生故障时间进行识别。

2) EMD分解所得的各个IMF分量包含并突出了热力参数传感器输出信号的局部特征。

3) 在训练RBF神经网络时，该方法只需要热力参数传感器正常状态下的样本，克服了热力参数传感器故障样本稀少的困难。

4) 在热力参数传感器故障情况下，该方法能够计算出热力参数传感器正常状态下的理论值，代替故障信号，维持热力系统的正常运行，实现容错控制。

[1] Zhang Junbo, Li Tianrui, Chen Hongmei. Composite rough sets for dynamic data mining[J]. Information Sciences, 2014, 257: 81-100.

[2] Zhang Junbo, Li Tianrui, Ruan Da, et al. Neighborhood rough sets for dynamic data mining[J]. International Journal of Intelligent Systems, 2012, 27(4): 317-342.

[3] Crespo F, Weber R. A methodology for dynamic data mining based on fuzzy clustering[J]. Fuzzy Sets and Systems, 2005, 150(2): 267-284.

[4] Flores R A. State of the art in the classification of power quality events an overview[C]∥Proceedings of the 10thInternational Conference on Harmonics Quality of Power. Rio de Janeiro, Brazil: IEEE, 2002: 17-20.

[5] 徐涛, 王祁. 基于小波包的多尺度主元分析在传感器故障诊断中的应用[J]. 中国电机工程学报, 2007, 27(9):28-32.

Xu Tao, Wang Qi. Application of multiscale principal component analysis based on wavelet packet in sensor fault diagnosis[J]. Proceedings of the CSEE, 2007, 27(9):28-32. (in Chinese)

[6] Huimin C, Ruimei Z, Yanli H. Improved threshold denoising method based on wavelet transform[J]. Physics Procedia, 2012, 33: 1354-1359.

[7] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society of London Series, 1998: 903-995.

[8] 钟佑明，赵强，周建庭. 实时经验模态分解的实现方法[J]. 振动、测试与诊断，2012，32(1)：68-72.

Zhong Youming, Zhao Qiang, Zhou Jianting. The implementation method of real-time empirical mode decomposition[J]. Journal of Vibration，Measurement & Diagnosis, 2012，32(1)：68-72. (in Chinese)

[9] 樊奕辰, 卢启鹏, 丁海泉, 等. 经验模态分解法在近红外无创血红蛋白检测中的应用研究[J]. 光谱学与光谱分析, 2013, 33(2):349-353.

Feng Yichen, Lu Qipeng, Ding Haiquan, et al. Study on the application of empirical mode decomposition to noninvasive hemoglobin measurement by NIRS[J]. Spectroscopy and Spectral Analysis, 2013, 33(2):349-353. (in Chinese)

[10]孙洁娣, 郝雅立, 温江涛, 等. 基于 EMD 的高压燃气管道泄漏信号欠定盲分离方法[J]. 振动与冲击, 2013, 32(18): 81-86.

Sun jieti, Hao Yali, Wen Jiangtao, et al. Underdetermined blind source separation method of pipeline leakage signals based on empirical mode decomposition[J]. Journal of Vibration and Shock, 2013, 32(18): 81-86. (in Chinese)

[11]Prieto-Guerrero A, Espinosa-Paredes G. Decay ratio estimation in boiling water reactors based on the empirical mode decomposition and the Hilbert-Huang transform[J]. Progress in Nuclear Energy, 2014, 71: 122-133.

[12]Georgoulas G, Loutas T, Stylios C D, et al. Bearing fault detection based on hybrid ensemble detector and empirical mode decomposition[J]. Mechanical Systems and Signal Processing, 2013, 41(1): 510-525.

[13]Huang Y, Schmitt F G. Time dependent intrinsic correlation analysis of temperature and dissolved oxygen time series using empirical mode decomposition[J]. Journal of Marine Systems, 2014, 130: 90-100.

[14]Khorramdel B, Marzooghi H, Samet H, et al. Fault locating in large distribution systems by empirical mode decomposition and core vector regression[J]. International Journal of Electrical Power & Energy Systems, 2014, 58: 215-225.

[15]Peng Zhike, Peter W T. A comparison study of improved Hilbert-Huang transform and wavelet transform: application to fault diagnosis for rolling bearing[J]. Mechanical Systems and Signal Processing, 2005，19(5): 974-988.

[16]张毅坤,麻晓畅,华灯鑫,等. 基于EMD-DISPO的Mie散射激光雷达回波信号去噪方法研究[J].光谱学与光谱分析,2011, 31(11):2996-3000.

Zhang Yikun, Ma Xiaochang, Hua Dengxin, et al. The Mie scattering lidar return signal denoising research based on EMD-DISPO[J]. Spectroscopy and Spectral Analysis, 2011, 31(11):2996-3000. (in Chinese)

[17]刘倩倩,王春艳,史晓凤,等. 基于RBF神经网络的较低浓度下同步荧光光谱的溢油鉴别[J]. 光谱学与光谱分析, 2012, 32(4):1012-1015.

Liu Qianqian, Wang Chunyan, Shi Xiaofeng, et al. Identification of spill oil species based on low concentration synchronous fluorescence spectra and RBF neural network[J]. Spectroscopy and Spectral Analysis, 2012, 32(4):1012-1015. (in Chinese)

[18]Huang M, Liu X, Li J, et al. Melt index prediction by RBF neural network with an ICO-VSA hybrid optimization algorithm[J]. Journal of Applied Polymer Science, 2012, 126(2):519-526.

[19]Poultangari I, Shahnazi R, Sheikhan M. RBF neural network based PI pitch controller for a class of 5-MW wind turbines using particle swarm optimization algorithm[J]. ISA Transactions, 2012, 51(5): 641-648.

[20]Dunia R, Qin S J, Edgar T F, et al. Identification of faulty sensors using principal component analysis[J]. Aiche Journal, 1996, 42(10): 2797-2812.

10.16450/j.cnki.issn.1004-6801.2016.04.013

中央高校基本科研业务费专项资金资助项目

2014-09-05；

2014-11-13

TH81; TK38

李蔚，女，1974年10月生，博士、副研究员。主要研究方向为热能工程。曾发表《Modeling a two-span rotor system based on the Hamilton principle and rotor dynamic behavior analysis》(《Journal of Zhejiang University-Science A (Applied Physics & Engineering)》2014,Vol.15,No.11)等论文。

E-mail:energy@zju.edu.cn

简介：盛德仁，男，1960年2月生，教授。主要研究方向为大型汽轮机的优化运行。

E-mail:shengdr@zju.edu.cn