基于GA优化IWNN的短时交通流量预测方法

吴 凡, 孙建红, 葛鹤银, 刘景夏

(1. 南京理工大学 电子工程与光电技术学院, 南京 210094；2. 中国人民解放军理工大学 通信工程学院, 南京 210007)



基于GA优化IWNN的短时交通流量预测方法

吴 凡1, 孙建红1, 葛鹤银1, 刘景夏2

(1. 南京理工大学 电子工程与光电技术学院, 南京 210094；2. 中国人民解放军理工大学 通信工程学院, 南京 210007)

由于交通流量的非线性、复杂性和不确定性，确定数学模型的预测方法难以满足交通管理控制中对预测精度和收敛速度的要求。为了对交通流进行准确、实时、高效的预测，提出将小波理论与神经网络相结合，并改进网络的训练过程从而构建改进型小波神经网络；同时运用遗传算法优化网络的初始权值，最终提高了预测精度，加快了收敛速度，避免陷入局部极小。通过仿真和分析，提出的方法具有较好的预测结果。

交通拥堵； 短时交通流量预测； 改进型小波神经网络； 遗传算法

0 引 言

近年来，随着智能交通系统的蓬勃发展，针对交通拥堵问题的智能交通系统两大核心子系统交通诱导和交通控制逐渐成为研究的热门课题。但无论是对于交通诱导还是交通控制系统来说，准确、实时、高效的交通流预测是这些系统实现的前提和关键[1-2]。

现阶段的短时交通流预测模型一般可分成两类:一类是以传统数学和物理方法为基础的预测模型(如时间序列模型和卡尔曼滤波模型等);另一类是以现代科学技术和方法(如模拟技术、神经网络、模糊控制等)为主要研究手段而形成的预测模型[3]。第一类方法已经难以满足人们对预测精度越来越高的要求，而第二类方法在一定程度上摆脱了建立精确数学模型的困扰，开辟了新的思路。

人工神经网络作为一种通用的非线性函数逼近工具，以其良好的非线性品质、灵活而有效的自组织学习方法在预测领域显示了极大的优势[4]。传统的BP神经网络模型存在着收敛速度慢和易陷入局部极小等缺陷。目前不少文献采用粒子群算法[5]、布谷鸟算法[6]等对BP神经网络参数进行优化，但这些算法没有改变隐含层的传递函数即神经网络对非线性函数拟合的基函数并没有改变，故预测精度有待进一步提高。目前关于小波理论与神经网络相结合的研究逐渐增多，小波神经网络(Wavelet Neural Network, WNN)作为两者的结合，继承了小波变换的优点，即对非平稳信号具有良好的时频局部特性和变焦能力,使网络对非平稳信号的逼近能力有了明显的提高[7-8]。由于小波神经网络的网络结构和训练方法没有改变，所以仍然存在收敛速度慢和易陷入局部极小等缺点。

本文针对收敛速度慢和预测精度较低以及易陷入局部极小等问题，提出改进型小波神经网络(Improved Wavelet Neural Network, IWNN)即在传统的小波神经网络训练过程中增加了动量项和自适应学习率，使预测精度得到进一步提高；同时运用遗传算法(Genetic Algorithm, GA)去优化小波神经网络的初始参数，通过遗传算法的全局搜索能力让网络避免陷入局部极小，加快了收敛速度，也为网络初始参数的选择提供了依据，增加了网络的稳定性。

1 小波神经网络的短时交通流预测

1.1 输入输出模型的建立

小波神经网络是以人工神经网络拓扑结构为基础，将小波基函数作为神经网络中隐含层节点的传递函数，信号前向传播的同时、误差反向传播的神经网络。小波神经网络的拓补结构如图1所示。

图1中，X1，X2，…，Xk是小波神经网络的输入参数;Y1，Y2，…，Ym是小波神经网络的预测输出;ωij和ωjk为小波神经网络的权值。

当输入信号序列为xi(i=1，2，…，k)时，隐含层的输出计算公式如下式所示：

(1)

式中：h(j)为第j个隐含层节点输出值；ωij为输入层和隐含层的连接权值；hj为小波基函数；bj为小波基函数hj的平移因子；aj为小波基函数hj的伸缩因子。

本文采用的小波基函数为Morlet小波函数，如下式所示：

(2)

根据小波神经网络的拓扑结构可以得出输出层的计算公式,如下式所示：

(3)

式中：ωjk为隐含层到输出层的权值；h(j)为第j个隐含层节点的输出；l为隐含层节点数；m为输出层节点数。

综合式(1)～(3)可以建立从输入到输出的映射关系，从而构建了小波神经网络的输入输出模型。

1.2 预测的参数修正

小波神经网络的输入输出模型是预测模型的基础框架，依据算法和数据对模型进行训练才能使模型具有预测功能。小波神经网络预测模型训练的关键就在于网络参数的修正。传统小波神经网络权值参数修正算法与BP神经网络的修正算法[9-10]类似，采用的是梯度下降算法，具体步骤如下：

(1) 计算网络预测误差：

(4)

式中：yn(k)为实际输出；y(k)为小波神经网络的预测输出。

(2) 根据网络预测误差对相应参数求偏导，从而计算得到小波神经网络参数的修正值。由于无论是传统还是改进的算法，对每个参数修正的方式是相同的，所以本文以ωij的修正方式来代表ωij、ωjk、ak、bk这四个参数的修正方式：

(5)

式中，η为学习速率。

(3) 依据计算的修正值修正小波神经的网络权值和小波基函数的系数：

(6)

式中，i为训练的次数。

根据误差修正小波神经网络权值和小波基函数的参数，使网络预测值逼近期望值，从而实现交通流的短时预测。

2 基于GA优化的IWNN的短时交通流预测

2.1 IWNN的参数修正

由于传统小波神经网络参数修正算法采用的是梯度下降算法，而梯度下降法有着收敛速度慢、易陷入振荡效应和局部极小的缺点[11]。本文针对这些缺点提出引入动量项和自适应学习率来改进小波神经网络的参数修正方法。修正的公式如下：

(7)

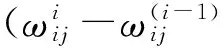
小波神经网络对动量项的学习速率η的取值往往是根据经验给出的固定值。但在网络训练的过程中，训练开始时效果较好的学习速率不一定适合后面训练过程。故提出用自适应学习率来替代传统的固定值学习速率，使学习率能够依据训练误差的变化来对自己进行动态调整。常见的自适应学习率算法[13-14]有很多，本文提出的自适应学习率如下式所示：

(8)

式中，e(k)表示第k次训练时网络的训练误差。

2.2 预测模型

改进型小波神经网络的初始结构仍采用随机初始化的方式。随机的初始化方式使网络的收敛速度、预测精度以及稳定性都没有保证，同时易陷入局部极小值。为了克服这些不足，需要一种全局搜索方式来避免搜索过程收敛于局部最优解。

遗传算法是一种并行随机搜索最优化方法。该算法从许多点开始并行操作，而非局限于一点，因此可以有效地防止搜索过程收敛于局部最优解。故本文采用遗传算法来对网络的初始结构参数进行优化。基于遗传算法优化改进型小波神经网络的短时交通流预测模型流程图如图2所示。

图2中关于遗传算法对网络初始结构优化的具体步骤如下：

图2 基于遗传算法优化改进型小波神经网络的短时交通流预测模型流程图

(1) 随机产生n个结构(即产生n个个体)，对每个结构进行编码，每个结构的编码长度为k×l+l+l+l×m。其中：k为输入节点数；l为隐含层节点数；m为输出节点数。

(2) 将小波神经网络的权值和小波基函数的参数按次序编成一个字符串作为问题的解。然后对编码后的初始群体(即n个个体)进行训练。

(3) 根据训练结果确定每个个体的适应度值。适应度的计算公式如下：

Fitness=1/(1+e)

(9)

式中，e为训练误差。

(4) 若遗传代数或适应度满足终止条件，跳至步骤7。

(5) 选择若干适应度大的个体，直接继承给下一代。同时用父代适应度最大的个体替代遗传操作后产生的最差个体。

(6) 对当前一代群体进行交叉和变异等遗传操作，产生下一代群体，跳至步骤(3)。

(7) 终止循环，得到最佳个体，解码还原相应值并将此值作为网络的初始参数。

3 实例分析

3.1 实验数据和网络结构

城市交通路网中交通路段某时刻的交通流量与本路段前几个时段的交通流量有关。所以可以根据实测路段交通流量的历史数据(交通流量的数据采集是每15 min一次，24 h不间断)，对该路段的交通流量进行短时交通流预测。由于一共采集了4 d的交通流量数据即384个时间点的数据，所以提出用前3 d共288个交通流量的数据来训练网络，最后用训练好的网络来预测第4 d 96个交通流量数据。

为预测路段t+1时刻的交通流量Qt+1，提出将该路段t时刻，t-1时刻，t-2时刻，t-3时刻，t-4时刻，t-5时刻的交通流量作为网络的输入节点，构建6维输入，1维输出的网络。根据文献[15]中的公式计算和分析，将隐含层节点数定为9。故本文采用的网络拓扑结构为6-9-1。

3.2 实例仿真结果分析

实验平台为CPU2.5GHz，windows8.1，Matlab 2014a的平台。为方便比较，实验中BP神经网络，WNN，IWNN，GA 优化IWNN均采用6-9-1网络拓扑结构，并且均进行多次训练和预测。网络最大训练次数均设为1 000，训练目标误差均设为0.05。在遗传算法中，设定初始种群规模为40，遗传代数为60，交叉概率为0.7，变异概率为0.1。

表1为四种预测模型预测效果对比。本文采用平均相对误差(MAPE)和迭代次数(epochs)作为模型预测性能的评价指标,并且每个预测模型均进行多次训练和预测，取记录数据的平均值作为表中参数。MAPE的定义如下式所示：

(10)

表1 四种预测模型预测结果的对比

BP神经网络，小波神经网络短时交通流量预测模型的预测值与交通流量实际值的对比曲线图如图3所示。

图3 BP神经网络和小波神经网络预测值与实际值的比较

观察图3和表1可以发现，BP神经网络已经具有了一定的预测能力。WNN模型的预测值曲线相比较BP神经网络模型而言更加贴合实际值曲线，表1中的数据也表明WNN模型的预测精度有着一定的增加。但是图3中仍然有个别时间点的预测值偏离实际值比较多，这表明预测模型的稳定性不高。

IWNN和GA优化IWNN预测模型的预测值与实际值的对比曲线图如图4所示。

图4 IWNN和GA优化IWNN预测值与实际值的比较

由图4和表1可知IWNN模型的预测精度相比较BP神经网络和WNN模型有着显著的提高。同时根据表1的迭代步数可知，IWNN预测模型的收敛速度与BP神经网络和WNN模型相比并没有提升。根据所记录的Epochs数据可以观察出IWNN预测模型的收敛过程存在缺陷，为进一步探究IWNN预测模型的缺点，本文将IWNN预测模型训练过程的随机10次迭代次数在图5中展示并且与GA优化IWNN预测模型的随机10次迭代次数进行比较。

IWNN和GA优化IWNN模型10次训练的迭代次数如图5所示。

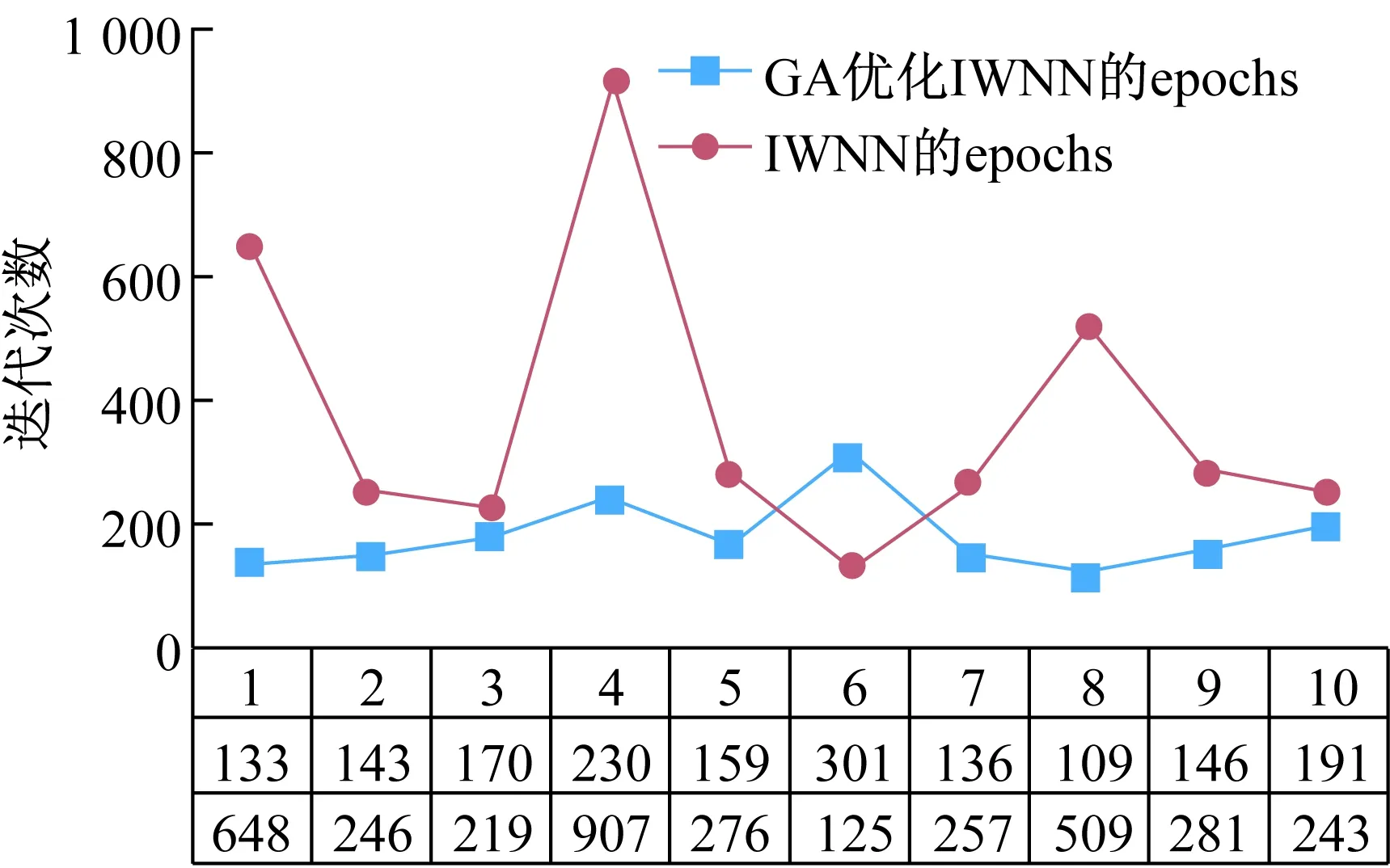
图5 IWNN和GA优化IWNN模型训练迭代次数的比较

通过图5可以发现，未经GA优化的IWNN预测模型的迭代次数不稳定且波动范围较大，分析该预测模型，发现造成上述问题的原因是IWNN预测模型的网络初始结构仍采用随机初始化的方式。反观GA优化的IWNN预测模型，迭代次数比较稳定且大部分的迭代次数低于IWNN预测模型。由于预测精度的增加会趋于饱和，根据表1可以发现GA优化并没有显著提高模型的预测精度。但结合图5和表1的数据可以发现通过GA优化可以有效减少训练的迭代次数即加快了收敛速度，同时也减小了迭代次数的波动范围即提高了预测模型的稳定性。

4 结 语

为解决短时交通流预测的难题，本文提出运用小波神经网络作为基础框架来构建预测模型。针对预测精度不高和收敛速度较慢等缺点提出引入动量项和自适应学习率来改进传统的小波神经网络，同时运用遗传算法优化改进后的小波神经网络。仿真实验表明：通过引入动量项和自适应学习率来改进的小波神经网络预测模型在预测精度上有着显著的提高。遗传算法的优化为网络初始参数的选择提供了可靠的依据，使预测模型在有着良好预测精度的同时也具备稳定性高和收敛速度快的优点。该预测模型稍加修改还可以应用于其他领域，值得进一步研究与实践应用。

[1] 贺国光,李 宇,马寿峰. 基于数学模型的短时交通流预测方法探讨[J]. 系统工程理论与实践,2000(12):51-56.

[2] 宋 驰，沈国江. 短时交通流预测模型综述[J]. 自动化博览,2012(6):84-87.

[3] 刘 静,关 伟. 交通流预测方法综述[J]. 公路交通科技,2004(3):82-85.

[4] 董景荣. 基于小波网络的非线性组合预测方法研究[J]. 系统工程学报,2000(4):383-388.

[5] 李 松,刘力军,翟 曼. 改进粒子群算法优化BP神经网络的短时交通流预测[J]. 系统工程理论与实践,2012(9):2045-2049.

[6] 赖锦辉,梁 松. 基于ACS优化BP神经网络的交通流量短时预测方法[J]. 计算机工程与应用,2014(10):244-248.

[7] Bashir Z, El-Hawary M E. “Short term load forecasting by using wavelet neural networks”[C]∥Proc The IEEE Conference on Electrical and Computer Engineering, Canadian: 2000, 163 - 166.

[8] Sheng-Tun Li, Shu-Ching Chen. Function approximation using robust wavelet neural networks[C]∥Proc The 14fh IEEE International Conference on Tools with Artificial Intelligence, Taiwan, 2002: 483-488.

[9] 胡金滨,唐旭清. 人工神经网络的BP算法及其应用[J]. 信息技术,2004(4):1-4.

[10] 余国强. 基于小波神经网络的短时交通流预测算法的研究[D].广州：华南理工大学,2012.

[11] 张国彬. 小波神经网络算法的改进与应用[D].福州：福州大学,2006.

[12] 孟维伟. 基于神经网络的交通量预测技术研究[D].南京：南京理工大学,2006.

[13] 于 涛. BP网络自适应学习率算法分析[D].大连：大连理工大学,2011.

[14] 李浩磊. 基于遗传算法优化小波神经网络的网络流量预测模型研究[D].西安：西安电子科技大学,2013.

[15] 许 东,吴 铮. 基于MATLAB6.x的系统分析与设计——神经网络.[M]. 2版. 西安：西安电子科技大学出版社,2002.

Short-time Traffic Flow Forecasting Method Based on Improved Wavelet Neural Network Optimized by GA

WUFan1,SUNJian-hong1,GEHe-yin1,LIUJing-xia2

(1. School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2. Institute of Communication Engineering, PLA University of Science and Technology, Nanjing 210007, China)

Traffic flow prediction is a very important research area of intelligent transportation system, and has a very important academic value and practical significance to improve the traffic congestion problems. Traditional prediction methods which used determined mathematical model would not meet the needs of prediction accuracy and convergence speed during the traffic management control because of nonlinear, complexity and uncertainty of traffic flow. In order to forecast traffic flow accurately, real-timely and efficiently, a new algorithm is proposed by combining wavelet theory and neural network, and constructing an IWNN(improved wavelet neural network) with improved network training methods. At the same time, the initial weights are optimized by GA(genetic algorithm). It can improve prediction accuracy, speed up the convergence speed and avoid entering local minima. The simulation results show that it can get better prediction results.

traffic congestion; short-time traffic flow forecasting; IWNN; GA

2015-05-06

江苏省产学研联合创新基金(BY2014004)

吴 凡(1992-)，男，江西九江人，硕士生，主要研究方向为嵌入式系统。Tel.：15250980510; E-mail: njustwufan@163.com

孙建红(1966-)，女，江苏张家港人，副教授，主要从事电路与系统的研究与教学。

Tel.：025-84303086; E-mail: sunjh@njust.edu.cn

TP 391.9

A

1006-7167(2016)05-0134-04