竖直平面内圆周运动的极值问题分析
罗定浩 辜振军
(湖北省利川市第一中学,湖北 利川 445400)
竖直平面内圆周运动的极值问题分析
罗定浩 辜振军
(湖北省利川市第一中学,湖北 利川 445400)
竖直面内的圆周运动是高中物理教学的重要内容,其中运动导致底座离地问题是一个难点,涉及受力分析、机械能守恒、牛顿运动定律、临界极值问题,本文对这个难点问题进行分析.
圆周运动;竖直面;临界极值问题
在物理教学中,经常会遇见一类物体在竖直平面内做圆周运动导致底座离地的题目,遇到这类题目时大多数学生认为只要小球通过最高点时底座不离地即可.但笔者认为实际情况并非如此,下面以实例具体阐述.
例1:如图1所示,在质量为M的电动机飞轮上固定着一个质量为m的重物,它到转轴的距离为r,为使电动机不从地面跳起,则电动机的飞轮角速度不得超过多少?
分析:重物转到飞轮的最高点时,若重物对飞轮的作用力恰好等于电动机的重力Mg时,电动机刚要跳起从而可求解电动机的角速度.
解答:重物转到飞轮的最高点时,电动机刚要跳起时,重物对飞轮的作用力F恰好等于电动机的重力Mg,即F=Mg.
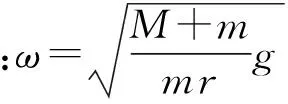
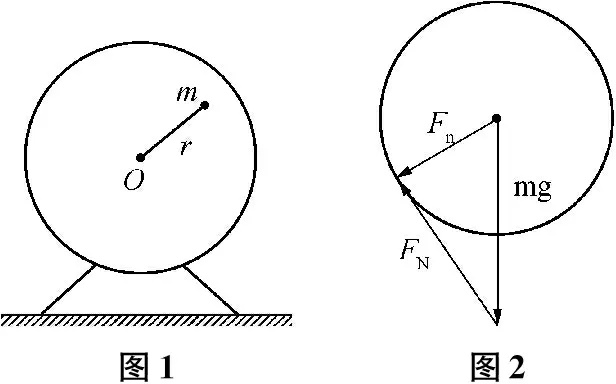
以上是大多数资料的解答,为什么重物转到最高点时为电动机不跳起的临界条件?笔者认为此处分析缺乏严密性.分析小球在竖直面内的圆周运动,如图2所示,由于小球在竖直面内做匀速圆周运动,故小球所受合外力Fn大小不变,始终指向圆心.当物体从最低点运动至最高点的过程中FN在竖直方向上的分量越来越小,当物体运动至最高点时FN在竖直方向上的分量最小,故物体运动至最高点时确实是底座不离开地面的临界条件,此时电动机的角速度取极大值,但不能作为结论,请看下面问题.
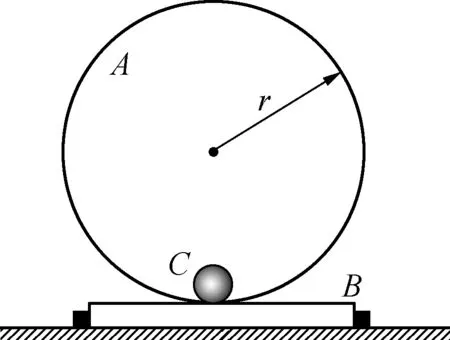
图3
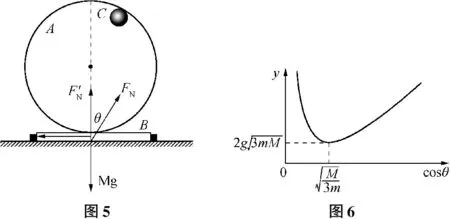
例2:如图3所示,A是半径为r的圆形光滑轨道,固定在木板B上,竖直放置;B的左右两侧各有一光滑挡板固定在地面上,使其不能左右运动,小球C静止放在轨道最低点,A、B、C质量相等.现给小球一水平向右的初速度v0,使小球在圆形轨道的内侧做圆周运动,为保证小球能通过轨道的最高点,且不会使B离开地面,已知重力加速度为g,则初速度v0必须满足的条件( ).
分析:小球运动至最高点对轨道恰好无压力时是v0最小的极值临界条件,小球运动至最高点对轨道的压力恰好等于2mg时是A、B离地时v0的极大值临界条件.
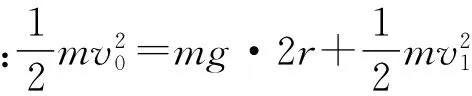

以上解答与很多资料一样,小球运动至最高点时A、B不离地为极值.笔者认为并不严谨,换一种解法如下.
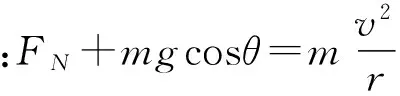
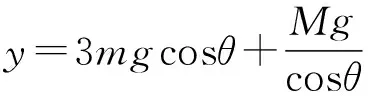
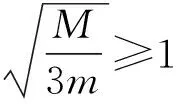
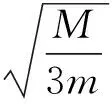
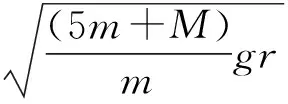
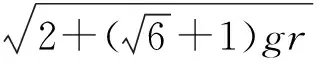
总之,物体在竖直平面内做圆周运动导致底座离地问题分析时,一定要看具体情形,不能盲目在最高、最低点取极值.同时在教学中,不要让学生套结论,而要用严谨的态度去解决实际问题.

