巧用平抛运动角度关系式 发展物理思维能力

徐飞翔

(安徽省灵璧县第一中学,安徽 宿州 234200)



巧用平抛运动角度关系式 发展物理思维能力

徐飞翔

(安徽省灵璧县第一中学,安徽 宿州 234200)

平抛运动中的速度与水平方向的夹角和位移与水平方向的夹角的关系式,在解决一些平抛运动及斜上抛运动的问题中经常用到.灵活运用该公式对培养学生分析解决问题的能力有很大的帮助.

平抛运动;角度关系;能力培养

平抛运动中有一个重要的角度关系式是近年来考查的重点，在教学中如何启发学生应用角度关系式分析、解决问题？笔者在教学实践中充分结合学生已有知识,采用“脚手架”的教学方法,结合运用角度关系式的变式训练,使学生分析、解决问题的能力得到逐步提高.

1 角度关系式推导——在已有知识基础上培养学生思维能力

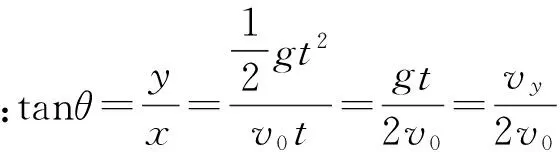
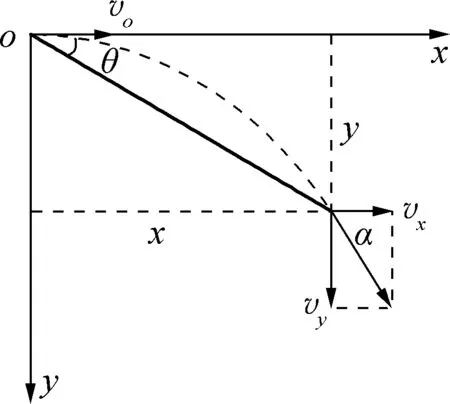
图1

2 灵活运用——在“最近发展区”提升学生思维能力

维果茨基的最近发展区理论认为在进行教学活动之前应该确定学生的两种发展水平,一种是学生现有的发展水平,一种是学生学习之后可能达到的发展水平,称之为最近发展区.在学生现有知识水平的基础上,灵活运用角度关系式,继续发展能力.

应用1:如图2所示,若从倾角为θ的斜面上同一位置,以不同速度向斜面下方水平抛出两个物体甲、乙,两个物体都落在斜面上时的速度方向与斜面的夹角分别为α1、α2,则有( ).

A.α1=α2B.α1>α2

C.α1<α2D.α1、α2的关系无法确定

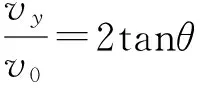
(1) 以不同初速度水平抛出的物体落在斜面上时各点的速度是互相平行的,选项A正确.

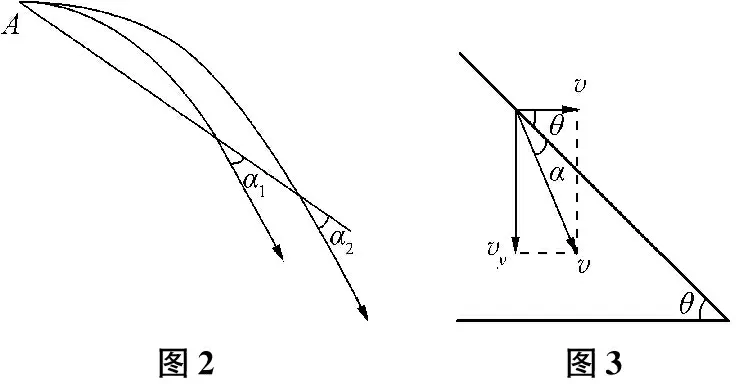
(2) 以不同速度从倾角为θ的斜面上水平抛出物体落在斜面上时,物体速度方向与斜面的夹角都为α=arctan(2tanθ)-θ.

在此基础上,继续拓展,促进学生思考,充分调动学生的积极性和主动性,以达到最近发展区.只有走在发展前面的教学才是好的教学,它使学生的潜在发展水平不断提高.

提出问题:如果从倾角为θ的斜面上,以与斜面的夹角为α=arctan(2tanθ)-θ、而速度大小不同斜向上抛出物体,当物体落在斜面上时情况会怎样？

分析问题:如果从倾角为θ的斜面上,以与斜面的夹角为α=arctan(2tanθ)-θ的不同速度斜向上抛出物体,落在斜面上时速度方向水平,即达到最高点，这个问题可以看做平抛运动的逆过程进行处理.

应用2:如图4所示,一质点以速度v从倾角为θ的斜面底端斜向上抛出,落到斜面上的M点且速度水平向右.现将该质点以2v的速度从斜面底端沿原方向抛出,落在斜面上的N点.不计空气阻力,下列说法正确的是( ).

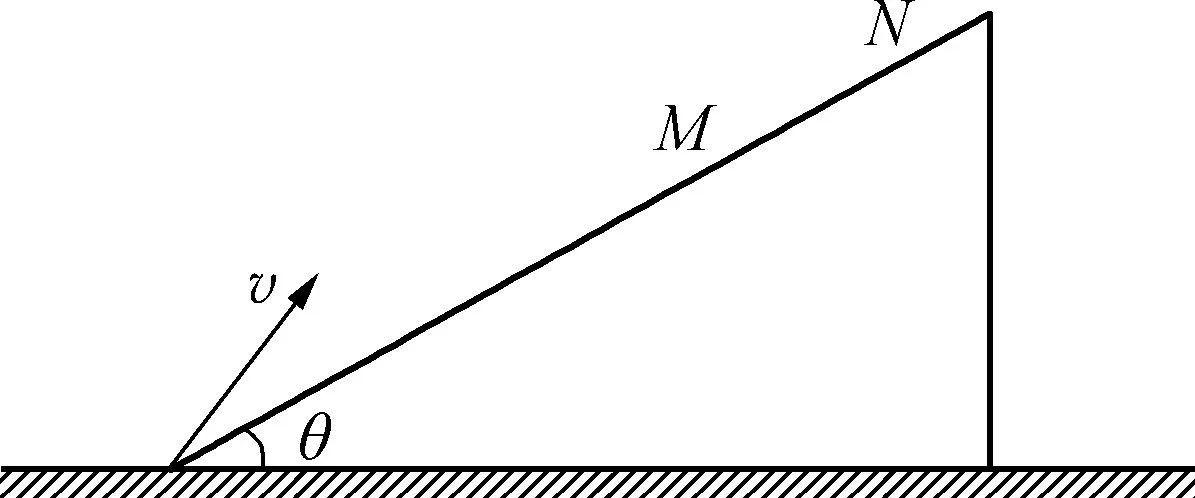
图4

A． 从出发点落到M和N两点,质点运动的时间之比为1∶2

B． 落到M和N两点速度之比为1∶1

C．M和N两点与斜面底端的高度之比为1∶2

D． 落到N点时速度方向水平向右

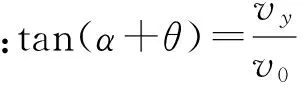
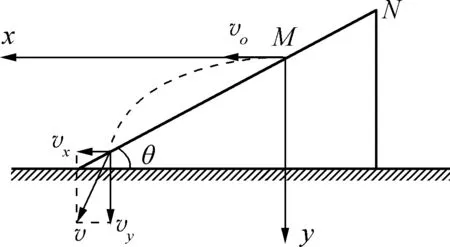
图5

可见,从斜面底端与斜面夹角为α斜向上抛出的物体落到斜面上时达到最高处,速度方向刚好水平,只要保持抛出时角度不变,无论速度大小如何变化,到达斜面上时,速度方向仍然水平,只是速度大小不同,到达的高度不同,水平速度的大小不同.依题意,若物体以2v的速度从斜面底端朝同样方向抛出,则落到N点时速度方向水平向右,可知D选项正确.

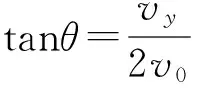
3 变式训练——在“脚手架”的基础上发展学生思维能力

在前面应用的基础之上,学生已经基本掌握分析问题的方法,此时拆除“脚手架”,进行变式训练,让学生提炼信息、联系知识、发展提高能力.

变式1:在篮球比赛的赛场上,一名球员在进行投篮的过程中，篮球恰好垂直打在篮板上,且篮球撞击篮板处与投出点之间的水平距离是竖直距离的2倍，空气阻力不计，篮球被投出时的速度与水平方向间的夹角为( ).

A. 30° B. 45° C. 60° D. 75°

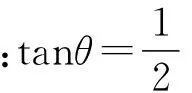
总之,以平抛运动的角度关系为切入点,以“脚手架”教学理论为依托,灵活运用变式训练法,对打造高效课堂、发展学生的思维能力,掌握平抛运动的规律,必起到事半功倍的效果.

[1]张方晓.“脚手架”模型支持学习环境设计研究[D].上海：华东师范大学,2004.

[2]郭晓霞.维果茨基最近发展区理论的应用与拓展[D].长春：吉林大学,2007.

[3]陆国新.“脚手架”理论在高三物理教学中的应用[J].湖南中学物理,2015,(8).