共享孔径多功能宽带阵列天线研究

李龙军,王布宏

(空军工程大学信息与导航学院,陕西西安 710077)

共享孔径多功能宽带阵列天线研究

李龙军,王布宏

(空军工程大学信息与导航学院,陕西西安 710077)

提出了一种基于子阵天线方向图频谱能量匹配的多子阵交错共享孔径宽带阵列天线设计方法.利用直线阵列天线单元激励与方向图之间存在傅里叶变换的关系,推导出子阵天线工作频率与单元激励之间的解析关系,在匹配各子阵天线激励值的基础上,采用密度加权阵的原理确定子阵天线单元的位置,实现不同工作频率下的子阵天线稀疏交错优化布阵.理论分析与实验仿真证明,该方法能够有效地抑制不同工作频率下子阵天线方向图的旁瓣峰值,使工作在不同频率下稀疏交错布阵的子阵天线方向图旁瓣峰值近似一致,抑制了栅瓣的产生,有效地拓宽了阵列天线的工作频带,实现了宽带阵列天线优化设计.

能量匹配;宽带阵列;密度加权阵;交错稀疏;傅里叶变换

随着电磁环境的日益复杂,对阵列信号处理应用范围及阵列天线的技术指标要求进一步提高,需要阵列天线能够处理不同频带的信号.设计宽带阵列天线可以提高天线的抗干扰能力和目标识别能力,有利于多功能阵列天线的实现[1-4].多子阵交错阵列天线的设计是实现宽带阵列天线最直接有效的方法之一,它要求子阵天线在不同中心频率工作时,各子阵天线的方向图性能能够保持近似一致.然而,工作频率的变化必然导致阵列天线孔径发生改变,这对阵列天线稀疏交错优化布阵带来了很多新的挑战,其核心问题是在满足阵列天线方向图和工作频带要求的前提下,如何有效地实现阵列天线的稀疏交错布阵.

为了解决这些问题,文献[5]提出利用循环差集(Cyclic Difference Set,CDS)和互补差集技术对阵列天线进行稀疏交错布阵,以此实现阵列天线的频带拓展.但由于该方法针对的是同一中心频率工作下的阵列天线稀疏交错优化,得到的共享孔径阵列天线只能实现宽带的有限拓展,在应用上有很大的局限性.文献[6]利用不同尺寸的天线单元和阵元间距设计出规则布阵的宽带阵列天线,该方法能够得到较大频带范围的阵列天线,但对天线单元本身的宽带性能要求比较高.文献[7]利用线极化的圆口径天线设计出宽带天线,有效地拓展了天线单元的频带宽度,但没能给出利用该天线设计宽带阵列天线的优化布阵方法.现有的宽带阵列天线设计方法主要以宽带天线单元的研究以及非均匀分布的稀疏宽带阵列天线的研究为主,这些方法实现起来较为复杂,且只能对阵列天线频带进行有限拓展,实用性受到限制[8].近两年,一些新的只能寻优算法相应出现(如入侵杂草算法),使得阵列天线设计方法有了更多的选择[9-10],但宽带阵列天线设计依然存在多维搜索的难题,这些难题尚待解决.

鉴于现有方法存在的种种问题,笔者提出一种不同工作频率下多子阵交错的宽带阵列天线设计方法.该方法利用天线单元激励与方向图之间存在的傅里叶变换关系[11-12],将阵列天线工作频率的差异转换为单元激励的变化,采用等倍数选取阵元激励的方法,利用密度加权的原理,确定不同工作频率下子阵单元的位置,使各子阵天线方向图的期望值相同和交错稀疏子阵方向图近似一致,通过子孔径频带的叠加最终实现宽带阵列天线的设计.相对于传统的宽带阵列天线的设计方法,该方法可以灵活地实现子阵工作频率比,在充分利用天线孔径的同时,通过少量的天线单元实现宽带阵列天线的设计,有利于系统成本的降低和单元互耦效应的抑制.

1　密度加权阵的基本原理

密度加权阵是根据统计学的原理,稀疏掉部分有源单元的阵列天线.Skolnik研究了一种统计的稀疏优化方法,当单元以等间隔均匀分布时,单元存在的概率与满阵的锥削度成正比.以一个阵元数为N、阵元间距为1/2的波长、入射方位角为θ的均匀线阵为例,当阵元均为理想的全向性单元时,其方向图可表示为

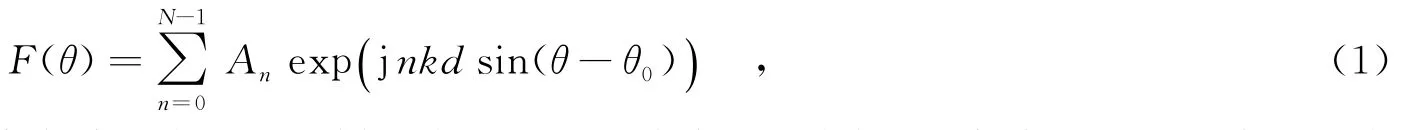
其中,k=2π/λ,λ为信号波长,θ0决定阵列方向图主瓣的方向,An为满阵的幅度加权.当阵列为稀疏阵列天线且阵列方向图主瓣指向零度时,

其中,In为0,1序列,“0”代表阵列单元被稀疏掉,“1”表示阵元保留.阵元在栅格点上存在的概率为

其中,Amax为满阵天线单元激励的最大幅值,m为稀疏常量.

2　宽带阵列天线设计的原理分析

对于等间隔均匀直线阵列,主瓣指向0°方向.当忽略阵元间互耦效应且阵元均为理想的全向性单元时,其方向图可表示为

对式(4)进行一维离散傅里叶逆变换,通常表示为

其中,M为周期;w0=2π/M,为采样间隔;t=0,1,…,M-1.由式(4)和式(5)可知,阵元的激励An与阵因子之间存在傅里叶变换的关系[12].若阵列天线是由不同工作频率下多个子阵(假设子阵数为4个)交错分布于同一个天线孔径上组成的,则子阵天线工作中心频率存在以下关系:

由λf=c可知,4个子阵对应的信号波长存在以下关系:

若栅格是以λ0/2为单位等间隔划分的,由于单元激励与阵列天线方向图之间存在傅里叶变换的关系,则4个子阵的方向图可以写为

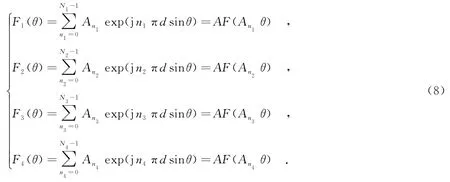
由式(3)可知,阵元存在的概率与阵列天线方向图之间是正比例的关系,因此阵列天线方向图可定义为概率事件,其期望值为

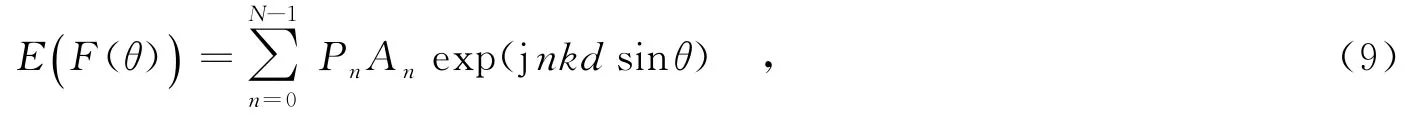
其中,Pn为单元存在的概率.根据交错阵列天线的优化目标可知,需要各子阵天线方向图近似一致.如何使4个子阵方向图的期望值相同,则需要消除中心频率不同对阵列天线方向图的影响.即当

时,各子阵单元存在的概率有以下关系:

因为阵元之间的间距是以波长为单位计量的(单元之间的间距为半波长的整数倍),从而在波数与单元间距相乘的过程中波长被抵消,故无须考虑频率变化对波数的影响.由式(9)和式(11)可知:

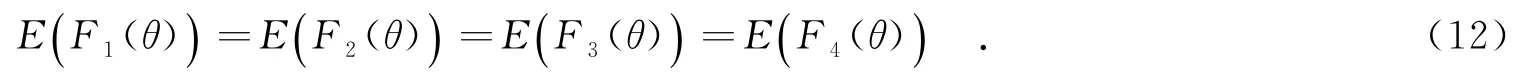
综上可知,当各子阵天线单元激励之间的比例关系与其工作频率之间的倍数关系一致时,各子阵天线方向图作为概率事件的期望值(均值)近似一致(即归一化方向图函数值近似一致).根据该理论可知,由子阵天线中心工作频率选取其单元所在的位置,就能最终实现工作在不同中心频率下的子阵天线方向图保持近似一致.

3　宽带阵列天线设计方法的基本流程

由于阵列天线单元激励与方向图之间存在傅里叶变换的关系,因此可以利用快速傅里叶变换的方法进行单元激励与方向图之间的转换,这样能极大地减小计算量,节省运算时间.笔者利用迭代快速傅里叶变换(Fast Fourier Transform,FFT)算法,通过改变迭代快速傅里叶变换算法的阵元位置选取方式,实现工作在不同中心频率下的多子阵交错优化布阵设计.对阵元数为N的直线阵列阵元激励进行K点的快速傅里叶逆变换,得到FA值.令FA旁瓣区域中大于约束旁瓣值的点上的值等于约束旁瓣,这样做的目的是为了使子阵天线方向图旁瓣峰值维持在一个较低的水平上.校正完成后,对新的FA进行K点的快速傅里叶变换,获得K个激励振幅Am.截取Am中的前N个值作为满阵激励,并对其进行由大到小排序,形成新的序列Af.确定各子阵天线工作频率的关系,若存在f0=a1f1=a2f2=a3f3,则在选取子阵天线单元激励时需要按照同等比例进行选取(即在选取时需要保证An1≈a1An2≈a2An3≈a3An4).将单元位置确定后的子阵天线单元激励值置为1.以子阵1方向图的旁瓣值作为目标函数进行下一次的迭代,以此来降低子阵的旁瓣峰值.通过该方式确定子阵天线单元位置能够使得各子阵天线方向图近似一致,且旁瓣值维持在一个较低的水平.算法的具体步骤如下:

(1)根据需要交错布阵的子阵个数S,以稀疏率1/S随机稀疏阵元数为N的直线阵列作为子阵1,设置稀疏后的子阵1的天线单元激励值Im为1.

(2)对Im进行K点的逆快速傅里叶变换,得到子阵1天线功率方向图函数的值FA.

(3)设置合适的约束旁瓣,对FA旁瓣区域的值进行判定,令幅值大于约束旁瓣值的点上的值为约束旁瓣值,其他点上的值保持不变.

(4)对校正后的FA进行K点的快速傅里叶变换,得到新的满阵天线的激励幅值Am.

(5)截取Am中的前N个值,对其进行由大到小排列,生成向量Af.根据已知的各子阵工作频率之间的关系,以同等比例关系选取各子阵天线单元的激励,以获得的激励栅格所在的位置作为相应子阵天线单元的位置,并将天线结构确定的子阵天线单元上的激励值置为1.

(6)判断新生成的子阵1阵列结构与迭代前相比是否变化.如果是,则重复步骤(4)～(6);否则,迭代终止,输出优化后的结果,实现子阵天线频带的叠加,完成共享孔径交错稀疏多功能宽带阵列天线的设计.

4　实验仿真与分析

为了验证上述方法的正确性,利用笔者提出的方法对阵元数为100的线阵进行4个子阵稀疏交错优化布阵,并对其方向图性能及方向图带宽进行分析.仿真参数为:阵元均为理想的全向性单元,单元数为100,稀疏率为25%.快速傅里叶变换运算点数的选取影响着天线方向图曲线光滑程度以及最终的求解精度和时间,通过大量的实验可知,一般取210可以在曲线光滑程度以及运算时间和精度上折中.笔者取快速傅里叶变换和逆快速傅里叶变换运算点数为1 024,取约束旁瓣峰值为-20 d B,4个子阵的工作频率分别为4f0,3f0, 2f0,f0.

4.1不同工作频率下阵列天线的交错稀疏优化布阵

所有仿真均是在MATLAB R2012b中完成的.由假设条件可知,子阵天线工作频率关系确定.利用笔者提出的方法,首先对以稀疏率为25%随机稀疏的100元线阵进行1 024点快速傅里叶变换,根据上节所提的流程选取子阵单元的激励值,以此确定各子阵天线单元的位置,仿真得到的4个子阵交错的直线阵列天线结构如图1所示.图1中,“0”代表该位置处的阵元被稀疏掉,“1”代表该栅格点处存在阵元.从图1可知,4个子阵交错分布于同一个天线孔径上,各子阵占有的物理空间近似相同.

图1　四子阵交错稀疏宽带阵列天线结构

天线的孔径占有率为

其中,Lsubarrayi为子阵i的孔径电尺寸长度,Larray为整个阵列的孔径电尺寸长度.根据式(13)可知,子阵1的孔径占有率为89%,子阵2的孔径利用率为93%,子阵3和子阵4的孔径占有率分别为96%和99%.由此可知,4个交错子阵充分利用了天线孔径,在保证资源利用的同时提高了天线的分辨力.交错稀疏的子阵天线方向图如图2所示.从图2中可知,交错分布的4个子阵天线方向图近似一致,子阵1的旁瓣峰值为-7.29 dB,子阵2的旁瓣峰值为-8.17 dB,子阵3的旁瓣峰值为-7.96 dB,子阵4的旁瓣峰值为-8.96 dB,子阵间旁瓣峰值最小差值为0.21 d B.但由于子阵天线的工作频率不一样,因此各子阵天线的相对孔径不一样,其中子阵1的工作频率为4 GHz,其天线孔径电尺寸最大,因此其主瓣宽度最窄,分辨力最好.从图2(b)中可知,子阵1的方向图零点主瓣宽度为2.4°,子阵2的方向图零点主瓣宽度为2.8°,子阵3的方向图零点主瓣宽度为5.6°,子阵4的方向图零点主瓣宽度为8°,其详细参数对比如表1所示.由以上结果可知,笔者提出的方法能够对工作在不同工作频率下的子阵天线进行有效的稀疏交错优化布阵.

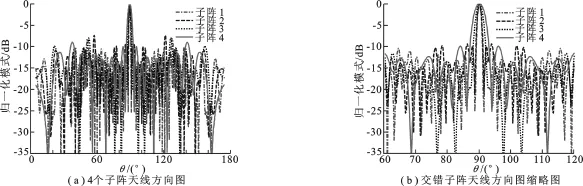
图2　不同工作频率下稀疏交错线阵的方向图

表1　稀疏交错宽带阵列天线性能对比

旁瓣约束值的选取直接影响了阵列采样点激励在前段的集中程度,其目的主要是为了降低子阵天线旁瓣峰值.当阵列天线为均匀满阵且单元激励不置1时,天线的旁瓣峰值能够满足约束要求,但由于稀疏子阵只选取了阵列天线的部分激励点且子阵天线单元激励值强制置为1,因此稀疏后的子阵天线方向图(部分激励点进行傅里叶变换获得的值)旁瓣峰值是无法满足约束要求的.选取一个合理的旁瓣约束值能够使目标方向图对应的激励点值集中分布在激励的前段部分,使得选取激励前段部分点值进行傅里叶逆变换得到的方向图旁瓣峰值能更好地接近约束旁瓣值,达到降低子阵天线方向图旁瓣值与约束旁瓣值之间差值的目的.因此,旁瓣约束值并不是越大越好或者越小越好.前期通过大量的仿真实验结果得出,在选取约束旁瓣峰值时,一般选小于同等阵元数均匀阵列旁瓣峰值10～15 d B的值优化效果最好.

4.2不同工作频率下稀疏交错阵列天线方向图带宽分析

为了进一步验证笔者所提方法的准确性和有效性,需对已经设计出来的交错稀疏阵列天线的方向图频带特性进行分析.假设各子阵工作在同一个工作频率下,中心频率为1 GHz.仿真选取的频带范围为0.5～2.5 GHz,栅格间距为半个波长,交错子阵天线方向图主瓣宽度随工作频率的变化关系曲线如图3(a)所示,4个子阵的旁瓣峰值随工作频率变化的关系如图3(b)所示.

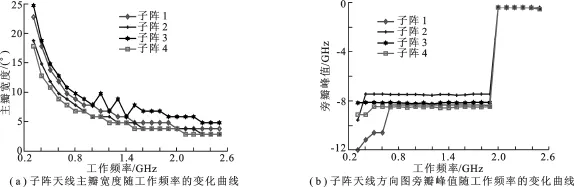
图3　4个子阵交错线阵方向图宽带性能

从图3(a)中可知,随着工作频率的增大,子阵天线方向图主瓣宽度减小.这是因为天线方向图与阵列孔径电尺寸有关.阵列的工作频率越大,波长越小,阵列天线的孔径电尺寸就越大,使得子阵天线方向图主瓣宽度越窄,分辨力越强.由图3(b)可知,4个子阵具有相同的带宽性能.当工作频率增大时,子阵天线方向图旁瓣峰值增大.以中心频率f0为1 GHz为例,当工作频率增大到2 GHz时,子阵天线方向图出现栅瓣;当阵列的工作频率小于1.9 GHz时,阵列天线方向图的峰值旁瓣维持在一个相对稳定的数值.因此可以认为,当4个子阵天线的工作频率是在同一个中心频率上,如1 GHz时,交错稀疏分布的4个子阵天线方向图的宽带为1.9 GHz.虽然对于均匀分布的线阵来说,稀疏阵列天线的带宽会有所增加,但增加的幅度有限,对设计宽带或者超宽带阵列天线应用的局限性很大.当基于不同中心频率设计多子阵稀疏交错阵列天线时,通过各子阵天线频带的叠加能有效拓展阵列天线的频带宽度.就文中所提例子而言,4个子阵工作在4个不同的频率下且能够保证4个子阵天线方向图性能近似一致,通过各子阵中心频率的叠加,阵列天线的频带宽度就从原先的1.9 GHz拓展成为4 GHz,而常用的通信信号如全球微波互联接入(Worldwide interoperability for Microwave Access,WiMAX)网络和C波段卫星通信系统分别为3.4～3.6 GHz和3.7～4.2 GHz,这就说明利用笔者提出的方法设计的4个子阵稀疏交错宽带阵列天线能够接收或者发射不同功能的信号,具备多功能天线性能.

5　结束语

笔者依据傅里叶变换的尺度压缩性质和密度加权阵的原理,在分析阵列天线工作频率与天线单元激励之间关系的基础上,首先将阵列天线工作频率的变化转换成为阵列天线单元激励变化,再利用快速傅里叶变换实现阵列天线方向图与单元激励之间的转换,通过约束天线方向图旁瓣峰值使交错稀疏分布的子阵天线方向图旁瓣峰值处于一个较低的水平,然后根据子阵设定的中心频率来选取子阵天线单元上的激励,根据密度加权阵中阵元激励与阵元位置之间的关系最终实现多子阵交错的宽带多功能阵列天线的设计.实验仿真表明,利用该方法能实现不同工作频率下子阵天线单元的有效稀疏交错布阵,得到的子阵天线方向图性能近似一致且能充分利用天线平台空间,不会造成资源的浪费.相对于传统的多子阵工作于同一个工作频率下进而实现宽带阵列天线设计的方法,该方法能更有效地拓展阵列天线的频带,实现宽带甚至是超宽带阵列天线的设计.

在实际应用中,可以通过调整各频段子阵的移相器的角度,使工作在不同频率下的子阵天线进行不同角度的空间扫描.若同时采用自适应波束形成技术,则还可以灵活控制波束指向,同时在干扰方向形成零点,从而进一步提高天线的抗干扰能力.

[1]WANG G G,GUO L,DUAN H,et al.A New Improved Firefly Algorithm for Global Numerical Optimization[J]. Journal of Computational and Theoretical Nano-science,2014,11(2):477-485.

[2]WILL P M N K.Synthesis of Thinned Planar Circular and Square Arrays Using Density Tapering[J].IEEE Transactions on Antennas and Propagation,2014,62(4):1555-1563.

[3]KHAN A A,BROWN A K.Null Steering in Irregularly Spaced Sparse Antenna Arrays Using Aperture Distributed Subarrays and Hybrid Optimizer[J].IET Microwaves,Antennas and Propagation,2014,8(2):86-92.

[4]NGUYEN T H,MORISHITA H,KOYANAGI Y,et al.A Multi-level Optimization Method Using PSO for the Optimal Design of an L-shaped Folded Monopole Antenna Array[J].IEEE Transaction on Antennas and Propagation, 2014,62(1):206-215.

[5]COMAN C I,LAGER I E,LIGTHART L P.A Deterministic Solution to the Problem of Interleaving Multiple Sparse Array Antennas[C]//Proceedings of 2nd European Radar Conference.Piscataway:IEEE,2005:263-266.

[6]CANTRELL B,RAO J,TAVIK G.Wideband Array Antenna Concept[J].IEEE Aerospace&Electronic Systems Magazine,2006,21(1):9-12.

[7]QIN Y,GAO S,SAMBELL A,et,al.Design of a Broadband Square-ring-slot Coupled Patch Antenna[J].Microwave and Optical Technology Letter,2005,47(5):454-457.

[8]BARBA M.Wideband and Dual-linear Polarization Patch Antenna[J].IEEE Transactions on Antennas and Propagation,2008, 56(5):1472-1476.

[9]刘燕,焦永昌,张亚明,等.入侵杂草优化算法用于阵列天线方向图综合[J].西安电子科技大学学报,2014,41(1): 29-33. LIU Yan,JIAO Yongchang,ZHANG Yaming,et al.Application of the Invasive Weed Optimization Algorithm to the Pattern Synthesis of Array Antennas[J].Journal of Xidian University,2014,41(1):29-33.

[10]刘燕,焦永昌,张亚明,等.混合入侵杂草算法用于阵列天线波束赋形[J].西安电子科技大学学报,2014,41(4): 94-99. LIU Yan,JIAO Yongchang,ZHANG Yaming,et al.Application of the Hybrid Invasive Weed Optimization Algorithm to the Shaped Beam Synthesis of Array Antennas[J].Journal of Xidian University,2014,41(4):94-99.

[11]du PLESSIS W P.Weighted Thinned Linear Array Design with the Iterative FFT Technique[J].IEEE Transactions on Antennas and Propagation,2011,59(9):3473-3477.

[12]王新宽,焦永昌,谭艳艳.自适应迭代傅里叶算法用于阵列方向图综合[J].西安电子科技大学学报,2013,40(4): 85-89. WANG Xinkuan,JIAO Yongchang,TAN Yanyan.Adaptive Iterative Fourier Technique Applied for Antenna Arrays Pattern Synthesis[J].Journal of Xidian University,2013,40(4):85-89.

(编辑:郭 华)

Research on the shared aperture multifunction wideband array antenna

LI Longjun,WANG Buhong
(School of Information and Navigation,Air Force Engineering Univ.,Xi’an 710077,China)

The paper presents a new technology for designing the shared aperture wideband array with multiple interleaved sub-arrays based on the energy match of sub-array excitation distribution.In view of the Fourier transform relationship between the array pattern and elements excitation,the mathematical relationship between the array working frequency and elements excitation is achieved.The interleaved thinned sub-arrays with different working frequencies are designed with the positions of the elements achieved by way of the energy match of sub-array excitation distribution and the theory of density weighted array.Theoretical analysis and experimental simulation show that the peak side-lobe levels of the interleaved sub-arrays under different working frequencies which are designed by the proposed method are restrained with the grating lobe suppressed.The multifunction wideband array is achieved as the working bandwidth of array antennas is broadened effectively.

energy match;wideband array;density weighted array;interleaved thinned array; Fourier transform

TN820

A

1001-2400(2016)04-0147-07

10.3969/j.issn.1001-2400.2016.04.026

2015-06-03 网络出版时间：2015-10-21

国家自然科学基金资助项目(61172148)

李龙军(1988-),男,空军工程大学博士研究生,E-mail:lilongjunboy@126.com.

网络出版地址：http://www.cnki.net/kcms/detail/61.1076.TN.20151021.1046.052.html