碳纳米管受介电泳作用三维运动仿真

王小冲,安立宝,龚 亮,陈 琰

(华北理工大学机械工程学院,河北省无机非金属材料重点实验室,河北唐山 063009)

碳纳米管受介电泳作用三维运动仿真

王小冲,安立宝,龚 亮,陈 琰

(华北理工大学机械工程学院,河北省无机非金属材料重点实验室,河北唐山 063009)

利用溶于介电液中的碳纳米管在外加交变电场作用下极化产生介电泳力和液体粘滞阻力的共同作用,建立了碳纳米管受力和运动模型;对碳纳米管的运动过程进行了仿真,得到了碳纳米管从特定初始点开始的三维运动轨迹和可以实现组装的碳纳米管初始点分布区域.计算了碳纳米管运动过程中所受介电泳力和速度的变化规律,距离电极间隙越近,碳纳米管受力和速度越大,最大分别能达到10-9N和105μm/s的数量级.仿真结果为碳纳米管介电电泳组装提供指导.

碳纳米管;介电泳;数学模型;仿真;三维运动轨迹

碳纳米管(Carbon Nano Tube,CNT)具备优异的电学、力学、热学性能以及良好的化学稳定性,因此,可被应用于众多领域,如场效应晶体管、场发射元件、互连线、传感器、催化剂载体以及新能源电极材料等[1-3].组装是上述大多应用得以实现的重要前提条件[4-5].碳纳米管组装常用的方法包括化学气相沉积[6]、流体排布法[7]、原子力显微镜直接组装法[8]和介电电泳组装[9]等.相对于其他组装方法,介电电泳组装具有操作简单、速度快和成本低的优点.因此,介电电泳法成为目前广泛使用的碳纳米管组装方法.

在外加交变电场作用下,介电液中的碳纳米管将被极化而产生介电泳力[10].此外,碳纳米管在介电液中运动,还会受到液体的粘滞阻力.为了更好地分析碳纳米管的介电电泳组装过程,笔者将建立碳纳米管的受力和运动数学模型,并依据所建模型对组装过程中碳纳米管的运动进行仿真,分析碳纳米管在运动过程中的受力和速度变化规律,得到碳纳米管三维运动轨迹,获取可以成功组装碳纳米管的初始点分布区域.

1　介电电泳模型

现有的介电电泳模型大都是基于有效偶极矩理论[11]建立的.该理论只有在偶极子长度小于电场的非均匀度,即“偶极子近似”条件成立时才适用.碳纳米管的直径为纳米级,长度一般在微米级[12],为长径比较大的一维材料.在距离电极间隙较近的地方,碳纳米管上各点所处位置的电场强度变化很大,即作为偶极子的碳纳米管的长度大于电场的非均匀度,“偶极子近似”条件不成立使得有效偶极矩理论不再适用.因此,需要建立新的适用于碳纳米管等一维纳米材料组装的介电电泳模型.

碳纳米管是由碳原子组成的一维纳米材料,可以假设碳纳米管为连续介质,对碳纳米管进行分段处理,划分后的每段满足“偶极子近似”条件.根据每段碳纳米管所在位置的局部电场,依据有效偶极矩理论计算出各段的介电泳力,然后再把各段介电泳力相加得到碳纳米管所受总的介电泳力[13].考虑到碳纳米管在电场中两端部分电场强度变化较大,中间部分场强变化较小[14],因此,两端部分的划分要比中间部分精细.

碳纳米管中间电场强度变化较小的部分划分成N1个圆柱体.对场强变化较大的碳纳米管两端进行精细划分,两端部分不再划分成圆柱体,而是划分成球体如图1所示,两端分别划分成N2/2个球体.

图1　碳纳米管分段示意图

第i(i=1,2,3,…,N1)个圆柱体所受的介电泳力为[15]

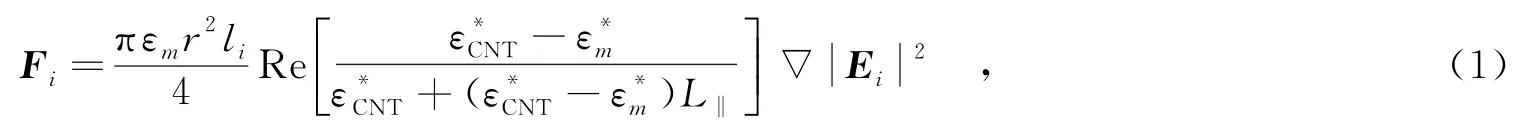
其中,r为碳纳米管的半径;li=(L-N2×2×r)/N1,为第i个圆柱体的轴向长度,其中L为碳纳米管的长度;Ei为第i个圆柱体的局部电场强度;和,分别为碳纳米管和介电液的复合介电常数,εCNT和εm分别为碳纳米管和介电液的介电常数,σCNT和σm分别为碳纳米管和介电液的电导率,ω=2πfe,fe为电场频率;,为去偏极系数.

第n(n=1,2,3,…,N2)个球体所受的介电泳力为[16]

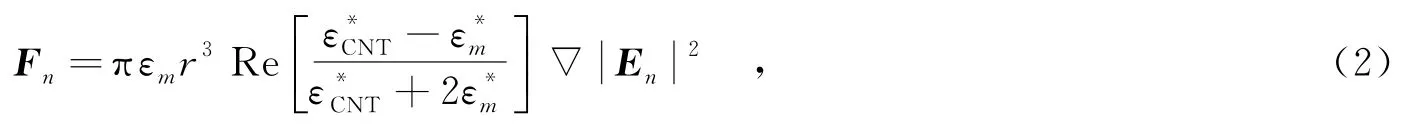
其中,En为第n个球体的局部电场强度.

碳纳米管所受到的总介电泳力为所有圆柱体段和球体段所受介电泳力之和FDEP.碳纳米管在介电液中受介电泳力作用运动时还会受到液体粘滞阻力的影响,碳纳米管的运动速度为[17]

在碳纳米管组装过程中,碳纳米管的轴向方向总是沿着电场线的方向[18].碳纳米管组装到电极上后由于静电力[19]和范德华力[20]的作用,碳纳米管被固定在电极上.碳纳米管自身重力大约为10-19N[17],相对于介电泳力(10-14～10-9N)而言,可以忽略不计.当粒子直径大于1μm时,布朗运动对粒子运动的影响非常小,布朗运动作用同样可以忽略不计[11].

2　仿真研究

仿真研究容易重复操作,研究成本低,还可以排除复杂的实验环境带来的影响.根据上述的介电电泳模型建立仿真模型,设定仿真参数,利用COMSOL Multiphysics软件进行仿真研究.在仿真结果中对电场和电场平方梯度的分布、碳纳米管运动过程中的受力和速度变化情况、碳纳米管的运动轨迹情况和可以成功组装碳纳米管的初始位置分布区域进行分析,得到了碳纳米管的受力和速度与碳纳米管到电极间隙距离之间的关系,以及形象直观的三维运动轨迹图.为了加快运算速度,根据电场的分布情况,在距离电极间隙远的地方仿真步长设置的较大,在距离近的地方步长设置的较小.

2.1仿真模型

图2为所建立的仿真模型图,模型中硅基片长宽均为60μm,厚度为10μm;二氧化硅覆盖在硅基片上,厚度为1μm;电极为金属铝,电极宽度为2μm,厚度为0.1μm,电极间隙为2μm.在电极上施加幅值为5 V, fe=100 k Hz的交流电,溶液完全覆盖二氧化硅基片,高度设置为30μm.

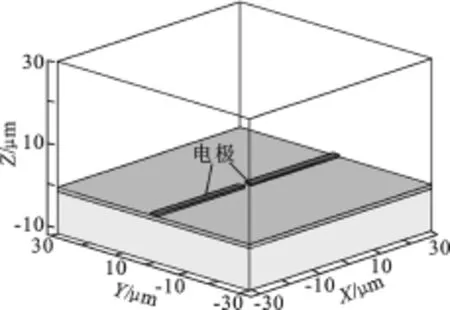
图2　三维运动轨迹仿真模型图

2.2仿真参数

仿真过程中碳纳米管设定为L=4μm,r=20 nm的多壁碳纳米管, N1=20,N2=6.介电溶液物理参数对仿真结果有着重要影响,文中综合文献选取异丙醇为介电液.异丙醇的粘度系数η=1×10-3Pa·s[14],真空绝对介电常数ε0=8.85×10-12F/m[10],各种材料电学参数如表1所示[14].

表1　模型中各种材料的电学参数[14]

2.3仿真结果

X-Y平面(Z=0)上电场强度的分布情况如图3(a)所示,从图中可以看出,在电极间隙处电场强度最强.在文中碳纳米管受正介电泳力作用,向电场强度大的区域运动[13],即碳纳米管向电极间隙运动.图3(b)仿真Y轴(X=0,Z=0)方向上Y=[-20μm,20μm]范围内的电场平方梯度分布情况,发现在电极间隙靠近电极尖端处电场平方梯度的值最大.由式(1)和式(2)可知,当碳纳米管到达该区域时受到的介电泳力也最大,同时在电极间隙的中间区域电场平方梯度变化较平稳,在此区域更容易实现碳纳米管组装,与文献[21]得出的结果一致.

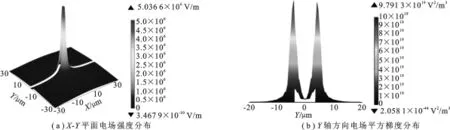
图3　电场强度分布和电场平方梯度分布

以碳纳米管从初始点(14.44μm,15μm,25μm)开始运动为例,对组装过程中碳纳米管受力和速度变化情况进行分析.从图4(a)中可以看出,随着碳纳米管到电极间隙距离的减小,碳纳米管所受的介电泳力逐渐增大,最大能达到10-9N的数量级.图4(b)描述的是随着碳纳米管到电极间隙距离的减小,碳纳米管的速度也在逐渐增大,最大速度能达到105μm/s的数量级,与文献[14]得出的结果近似.比较图4(a)和(b)发现,碳纳米管受力和速度随距离的变化趋势是一致的,即当碳纳米管受力较大时,运动速度也会相应地很大.

图5(a)所示为碳纳米管从初始点(14.44μm,15μm,25μm)开始运动的三维运动轨迹.从图中可以看出,碳纳米管在组装过程中不断向电极间隙位置靠近,其轴线方向和电场线方向始终保持一致.组装完成时碳纳米管左端和左侧电极刚好接触,同时顺着电场线方向排列,如图5(b)所示,与文献[18]实验观察到的结果相同.点(14.44μm,15μm,25μm)就是可以成功组装碳纳米管到电极间隙上的空间区域的一个临界位置.

图4　介电泳力和速度随碳纳米管到电极间隙距离的变化

图5(c)描绘了碳纳米管从初始点(0μm,0μm,25μm)开始运动的三维运动轨迹.从图中可以看出,碳纳米管在组装过程中一直处在电极间隙正上方的位置,并且轴线方向和电场线的方向保持一致.碳纳米管组装完成后两端与电极接触长度相等,同时顺着电场线方向排列,如图5(d)所示.由图5可知,碳纳米管如果从比临界位置更靠近电极间隙的初始点开始运动,则碳纳米管能够组装到电极上.

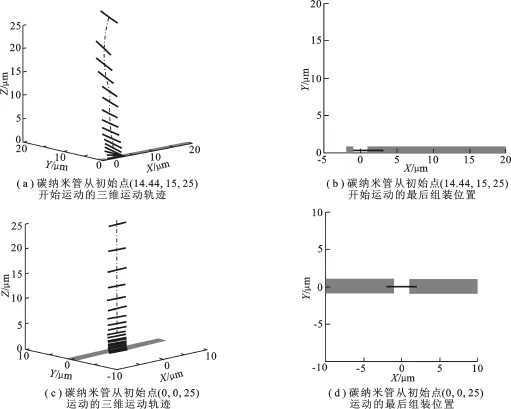
图5　碳纳米管三维运动轨迹及最后组装位置示意图

在坐标系统的第一象限内找到高度Z=25μm的6个初始点,从这6个初始点开始运动的碳纳米管恰好可以组装到电极上,如图6所示,这6个点所在位置就是碳纳米管恰好能够组装到电极上的临界位置.从图6碳纳米管的6条运动轨迹可以看出,如果初始点在6条运动轨迹的包络面与YZ面、XZ面所围成的区域内,碳纳米管就可以组装到电极间隙上.由于模型中电场是对称分布的,其余3个象限内的碳纳米管恰好可以组装到电极上的临界点与第一象限内的临界点是对称分布的.4个象限内的临界点及其运动轨迹可以围成一个三维空间初始点分布区域,如果碳纳米管的初始点在这个区域内,则碳纳米管就可以实现组装.

图6　第一象限内的6个临界初始点及碳纳米管运动轨迹

3　结 论

笔者建立了适合碳纳米管等一维纳米材料的介电电泳组装数学模型.通过对碳纳米管分段减小了偶极子长度,使每段碳纳米管满足“偶极子近似”条件.采用每段碳纳米管所在处的局部电场计算各段所受介电泳力,然后累加求得碳纳米管所受总的介电泳力,提高了模型的计算精度.仿真中考虑了介电泳力和液体粘滞阻力的共同作用,碳纳米管所受重力和布朗运动作用很小而忽略不计.

随着碳纳米管到电极间隙距离的减小,碳纳米管所受的介电泳力和运动速度增大,两者随距离变化曲线的趋势一致,最大分别达到10-9N和105μm/s的数量级,且碳纳米管在运动过程中其轴线方向与电场线方向始终保持一致.文中得到了碳纳米管三维运动轨迹和可以成功组装碳纳米管的初始点分布区域,揭示了碳纳米管在介电泳力和液体粘滞阻力共同作用下的运动规律,将为进一步分析碳纳米管介电电泳组装过程和参数优化提供帮助.

[1]李玉魁,李德昌,朱长纯.新型阴极粘贴技术制备三极CNT-FED的研究[J].西安电子科技大学学报,2005,32(2): 314-317. LI Yukui,LI Dechang,ZHU Changchun.The Fabrication of the Triode CNT-FED with New Cathode-pasting Technology[J].Journal of Xidian University,2005,32(2):314-317.

[2]RAKOV E G.Carbon Nanotubes in New Materials[J].Russian Chemical Reviews,2013,82(1):27-41.

[3]刘红霞,宋久旭,张鹤鸣.(4,4)碳纳米管/碳化硅纳米管异质结的输运特性[J].西安电子科技大学学报,2010,37 (3):520-523. LIU Hongxia,SONG Jiuxu,ZHANG Heming.Electronic Transport Properties of a(4,4)Carbon Nanotube/Silicon Carbide Nanotube Heterojunction[J].Journal of Xidian University,2010,37(3):520-523.

[4]NAIENI A K,NOJEH A.Dielectrophoretic Deposition of Carbon Nanotubes:The Role of Field Frequency and Its Dependence on Solution Conductivity[J].Microelectronic Engineering,2014,114(2):26-30.

[5]YAN Y H,CHAN-PARK M B,ZHANG Q.Advances in Carbon-Nanotube Assembly[J].Small,2007,3(1):24-42.

[6]CHEN Y B,ZHANG J.Chemical Vapor Deposition Growth of Single-Walled Carbon Nanotubes with Controlled Structures for Nanodevice Applications[J].Accounts of Chemical Research,2014,47(8):2273-2281.

[7]谭苗苗,叶雄英,王晓浩,等.流体排布与介电电泳结合排列组装碳纳米管[J].纳米技术与精密工程,2010,8(5): 389-393. TAN Miaomiao,YE Xiongying,WANG Xiaohao,et al.Combining Fluidic Alignment with Dielectrophoresis to Assemble Carbon Nanotubes[J].Nanotechnology and Precision Engineering,2010,8(5):389-393.

[8]POSTMA H W C,SELLMEIJER A,DEKKER C.Manipulation and Imaging of Individual Single-walled Carbon Nanotubes with an Atomic Force Microscope[J].Advanced Materials,2000,12(17):1299-1302.

[9]AN L,FRIEDRICH C R.Dielectrophoretic Assembly of Carbon Nanotubes and Stability Analysis[J].Progress in Natural Science:Materials International,2013,23(4):367-373.

[10]OLIVA-AVILÉS A I,AVILÉS F,SOSA V,et al.Dielectrophoretic Modeling of the Dynamic Carbon Nanotube Network Formation in Viscous Media under Alternating Current Electric Fields[J].Carbon,2014,69(4):342-354.

[11]MORGAN H,GREEN N G.AC Electrokinetics:Colloids and Nanoparticles[M].Philadelphia:Research Studies Press,2003.

[12]李德昌,李玉魁,李昕,等.碳纳米管薄膜阴极的制备及分析[J].西安电子科技大学学报,2005,32(6):877-880. LI Dechang,LI Yukui,LI Xin,et al.The Preparation and Analysis of the Carbon Nanotube Film Cathode[J].Journal of Xidian University,2005,32(6):877-880.

[13]TAO Q,JIANG M,LI G.Simulation and Experimental Study of Nanowire Assembly by Dielectrophoresis[J].IEEE Transactions on Nanotechnology,2014,13(3):517-526.

[14]AN L,FRIEDRICH C R.Process Parameters and Their Relations for the Dielectrophoretic Assembly of CarbonNanotubes[J].Journal of Applied Physics,2009,105(7):074314.

[15]BERGER S D,MCGRUER N E,ADAMS G G.Simulation of Dielectrophoretic Assembly of Carbon Nanotubes Using 3D Finite Element Analysis[J].Nanotechnology,2015,26(15):155602.

[16]BANERJEE S,WHITE B,HUANG L,et al.Precise Positioning of Carbon Nanotubes by Ac Dielectrophoresis Using Floating Posts[J].Applied Physics A,2007,86(4):415-419.

[17]KIM J E,HAN C S.Use of Dielectrophoresis in the Fabrication of an Atomic Force Microscope Tip with a Carbon Nanotube:a Numerical Analysis[J].Nanotechnology,2005,16(10):2245-2250.

[18]YANG B,YANG Z,ZHAO Z,et al.The Assembly of Carbon Nanotubes by Dielectrophoresis:Insights into the Dielectrophoretic Nanotube--Nanotube Interactions[J].Physica E,Low-dimentional Systems and Nanostructures,2014, 56(2):117-122.

[19]MAYER A,LAMBIN P.Calculation of the Electrostatic Forces that Act on Carbon Nanotubes Placed in the Vicinity of Metallic Protrusions[J].Nanotechnology,2005,16(11):2685-2695.

[20]HIROTANI J,IKUTA T,NISHIYAMA T,et al.Measuring the Thermal Boundary Resistance of Van Der Waals Contacts Using an Individual Carbon Nanotube[J].Journal of Physics:Condensed Matter,2013,25(2):025301.

[21]KWON S G,KIM S H,KIM K H,et al.Distribution of Electric Field for Carbon Nanotube Assembly:Simulation(I) [J].The Chinese Journal of Nonferrous Metals,2011,21(11):117-120.

(编辑:李恩科)

Three-dimensional simulation of kinetics of carbon nanotubes under dielectrophoresis

WANG Xiaochong,AN Libao,GONG Liang,CHEN Yan
(College of Mechanical Engineering,Hebei Provincial Key Lab.of Inorganic Nonmetallic Materials, North China Univ.of Science and Technology,Tangshan 063009,China)

Based on the dielectrophoretic force arising from the polarization of carbon nanotubes(CNTs)in the dielectric fluid under an alternating current electric field and the viscous resistance from the fluid,force and motion models for CNTs under dielectrophoresis(DEP)are established.Simulation is conducted on the translational and rotational motion of CNTs.Three-dimensional trajectories and a distribution region of initial points from where a CNT can be successfully assembled onto the electrode gap are obtained.By calculating the DEP force and translational velocity of a CNT during assembly,we know that the nearer the CNT to the electrode gap,the greater the DEP force and CNT velocity,and that the maximal DEP force and CNT velocity can be respectively of orders 10-9N and 105μm/s.The results of simulation provide guidance for DEP assembly of CNTs.

carbon nanotube;dielectrophoresis;mathematical model;simulation;three-dimensional trajectory

TN4

A

1001-2400(2016)04-0154-06

10.3969/j.issn.1001-2400.2016.04.027

2015-04-09 网络出版时间：2015-10-21

国家自然科学基金资助项目(51172062,51472074);河北省引进海外高层次人才“百人计划”资助项目(E2012100005)

王小冲(1990-),男,华北理工大学硕士研究生,E-mail:purplean@163.com.

安立宝(1965-),男,教授,博士,E-mail:lan@ncst.edu.cn.

网络出版地址：http://www.cnki.net/kcms/detail/61.1076.TN.20151021.1046.054.html