RLN衰落下D-MIMO系统遍历容量上边界

王咏平,曹汉强,王安稳

(1.华中科技大学电子信息与通信学院,湖北武汉 430074; 2.海军工程大学理学院,湖北武汉 430033)

RLN衰落下D-MIMO系统遍历容量上边界

王咏平1,曹汉强1,王安稳2

(1.华中科技大学电子信息与通信学院,湖北武汉 430074; 2.海军工程大学理学院,湖北武汉 430033)

针对空域双边相关同时存在、收发天线数量不受限制的RLN衰落下的分布式多输入多输出系统,分析和提出了解析的系统遍历容量的上边界.通过子矩阵展开等方法构造出新的不等式,在对上述系统模型的遍历容量边界分析中,解决了对大尺度衰落矩阵和小尺度衰落矩阵的统计分析无法分离的问题.当系统接收端天线数量大于或小于等于发送端时,在低信噪比到高信噪比的范围内,上边界均非常接近遍历容量.这一结论由不同空域相关系数下的仿真试验所证实.当分布式系统的收发端站点数量均为1时,模型退化为点对点多输入多输出系统,该上边界变为空域双边相关Rayleigh衰落下多输入多输出系统遍历容量的上边界.

通信系统;衰落信道;多输入多输出;分布式系统;遍历容量

目前,基于不同的空域相关性假设和不同的衰落类型假设,众多研究[1-2]广泛探讨了点对点多输入多输出(Multiple-Input Multiple-Output,MIMO)系统的信道容量.近来,关于分布式多输入多输出(Distributed Multiple-Input Multiple-Output,D-MIMO)系统的研究正在增加.该系统同时具有MIMO系统的微观分集增益(空间多路增益)和分布式天线系统的宏观分集增益.D-MIMO系统与点对点MIMO系统的本质区别在于它将MIMO无线信道一端的天线划分为空间上分离的多个无线端口.于是,经由不同传播路径,各无线连接具有不同的路径损耗及阴影效应(大尺度衰落).这一点与传统点对点MIMO系统不同,对D-MIMO系统的分析带来困扰.由此,只有少量研究工作分析组合衰落(小尺度衰落和大尺度衰落)对D-MIMO系统信道容量的影响[3-8].

为了便于分析D-MIMO系统遍历容量,一些研究采用Gamma分布或逆高斯(Inverse-Gaussian,IG)分布作为经典lognormal分布的近似[3-5]来刻画阴影效应.但是,这些近似方法并不能精确描述lognormal分布.为了更精确地描述D-MIMO系统的Rayleigh/lognormal信道模型,文献[8]使用Gauss-Hermite多项式求出了系统传输总速率的数值近似解.文献[6]给出了接收端使用迫零(Zero Fording,ZF)接收器、仅接收端空间相关性存在并且接收天线数量不小于发送天线数量时,系统传输总速率的上下边界.当空域双边相关同时存在时,文献[7]仅给出了接收与发送天线数量相等时的遍历容量下边界.

与文献[6-8]不同,笔者提出的系统模型为任意收发天线数量下空域双边相关(接收相关与发送相关)同时存在时Rayleigh/Lognormal衰落下的D-MIMO系统.并且在该模型中,收发端天线数量的对比关系不受限制.文中通过子矩阵展开等方法,构造出一个新的不等式,再通过对复二次型分布和对数正态分布的分析,给出了解析的遍历容量上边界.由于采用了以上方法,笔者解决了文献[6-8]没有解决的关于双边相关同时存在且收发端天线数量不受限制时,信道容量边界分析中对大尺度衰落矩阵和小尺度衰落矩阵的统计分析无法分离的问题.

1　系统模型

设定一个D-MIMO系统,系统接收端有NR根天线,发送端有L个发送节点,每个节点有NT根天线.系统中输入输出关系表示为

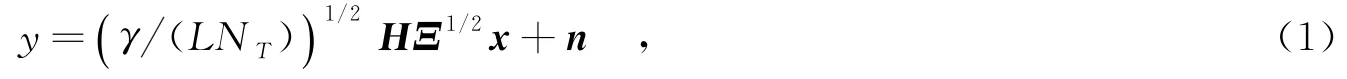
其中,HW的元素独立同分布(independent identically distributed,i.i.d.),而且HW的元素服从均值为0、方差为1的正态分布(CN(0,1)).RR和RT为接收相关矩阵与发送相关矩阵,这两个矩阵均为复对称的正定矩阵.由于L个发送节点在空间上分离,发送相关仅存在于同一节点的天线之间.这一模型称为Kronecker模型.在式(1)所表示的系统中,仅接收端已知信道状态信息(Channel Statement Information,CSI),因此发送功率被平均分配到每根发送天线.

其中,Dm(m=1,…,L)表示发送端第m个节点与接受端的距离.而v是路径损失指数,其取值范围通常为2至6.在文中,Ξ表示的大尺度衰落服从对数正态分布[6-8],ξm的概率密度函数为

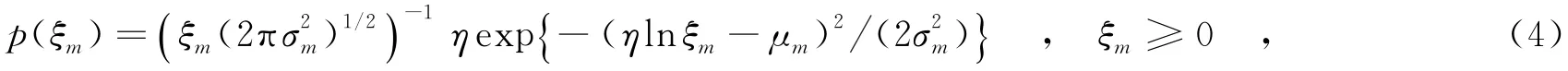
其中,η=10/ln10,μm/η为lnξm的均值,σm/η为lnξm的标准差.

2　遍历容量上边界

2.1遍历容量

在式(1)所表示的系统中,仅接收端已知信道状态信息,因此发送功率被平均分配到每根发送天线.于是,根据式(1)、(2)和文献[1]给出的结论可知,D-MIMO系统式(1)的遍历容量为

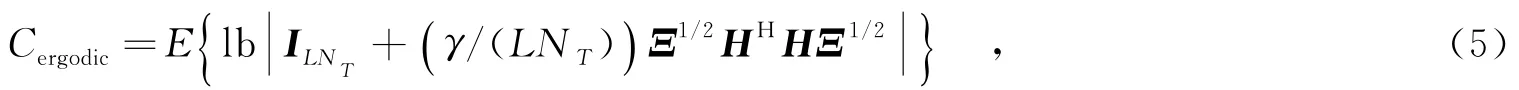
2.2行列式的展开

其中,τk={l1,…,lk}∈{1,…,n},且l1＜…＜lk.k阶矩阵Sτk由位于矩阵S第l1,…,lk行l1,…,lk列的元素构成.

2.3当NR＞LNT时的上边界

当收端天线数量大于发端,即NR＞LNT时,由式(6)给出的行列式展开式,文中将信道遍历容量式(5)展开,再由log(1+x)的凹凸性,和Jensen不等式推导出下列不等式: k

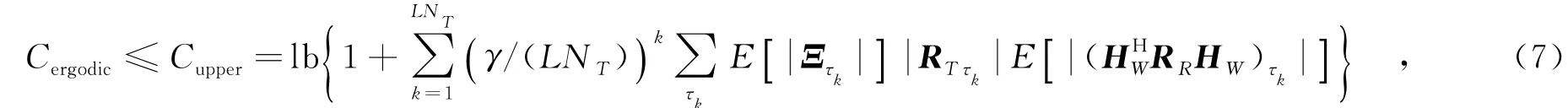
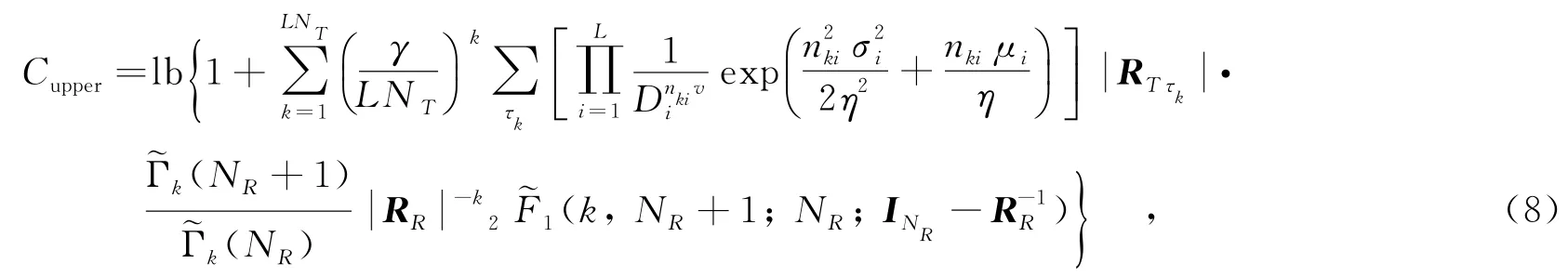
2.4当NR≤LNT时的上边界

当接收端天线数量小于等于发端,即NR≤LNT时,根据式(6)给出的行列式展开式,将信道遍历容量式(5)展开,再由不等式的凹凸性及Jensen不等式得出

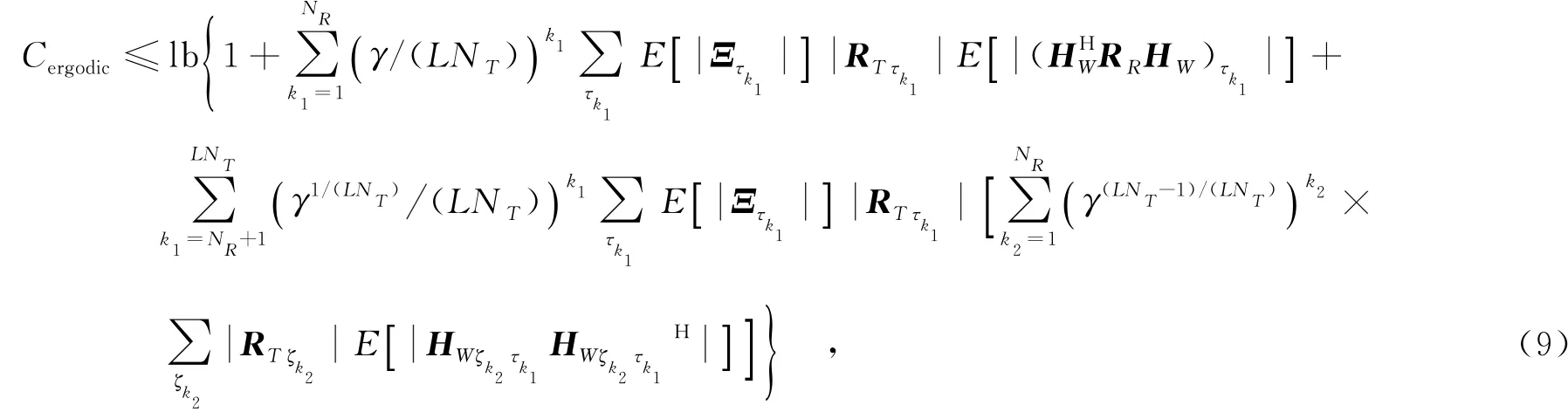
其中,ζk={h1,…,hk}∈{1,…,NR},且h1＜…＜hk.式(9)中,E分别由下文式(12)、(15)和(17)给出,将其代入式(9),求出NR≤LNT时信道遍历容量上边界为

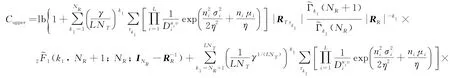
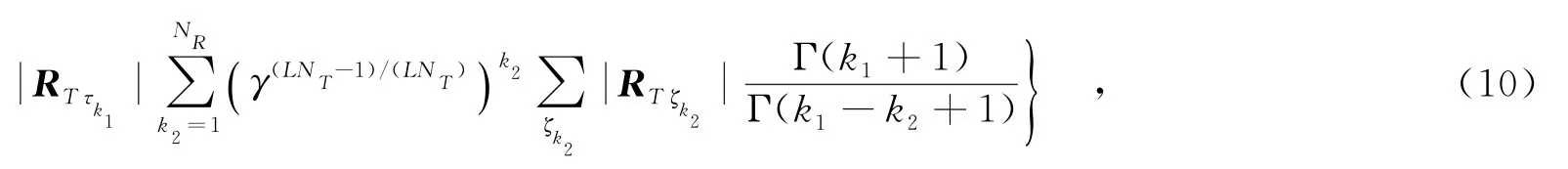
其中,nki为中属于集合{(i-1)NT+1,…,iNT}的元素的数量,,超几何函数21(·)的值由下文式(18)给出.

3　遍历容量上边界的分量

由文献[10]可知,若矩阵x∈Cp×n满足x～Np,n(0,Σ⊗In),n≥p,则S=XXH服从Wishart分布,其概率密度函数为

由文献[10]知,若矩阵X∈Cp×n满足X～Np,n(0,Σ⊗In),n≥p,则二次型S=XA XH概率密度函数为

超几何函数定义为

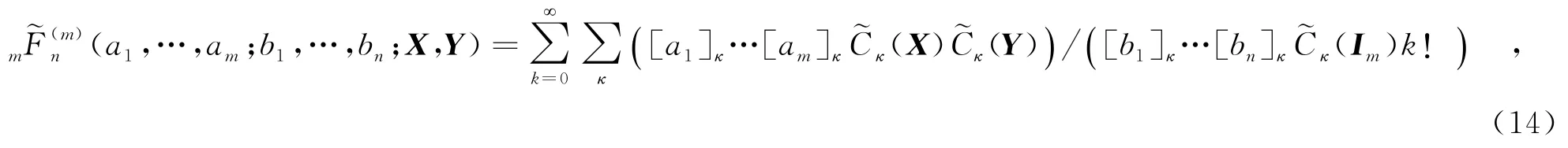
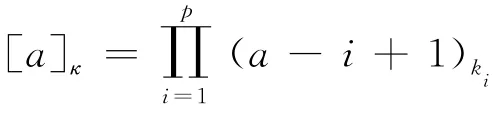
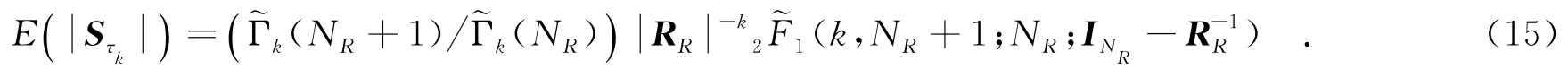
由于ξm服从对数正态分布,根据式(4)给出的概率密度函数,ξam的期望值为

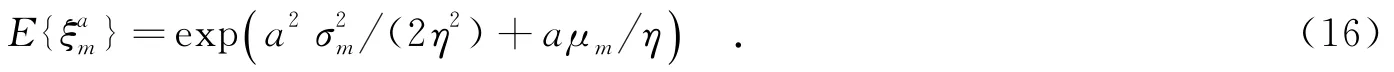
将集合τk={l1,…,lk}∈{1,…,LNT},l1＜…＜lk中属于集合{1,…,NT},{NT+1,…,2NT},…, {(L-1)NT+1,…,LNT}的元素的数量,分别记为nk1,nk2,…,nkL.于是,由式(4)、(16)导出

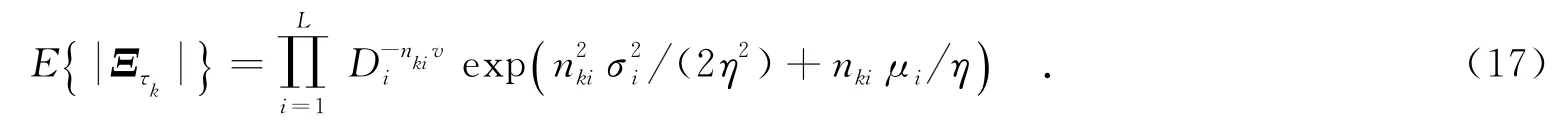
3.4关于超几何函数的推论

根据超几何函数的定义及性质,文中导出式(8)、(10)和式(15)中的超几何函数的计算方法[11]为

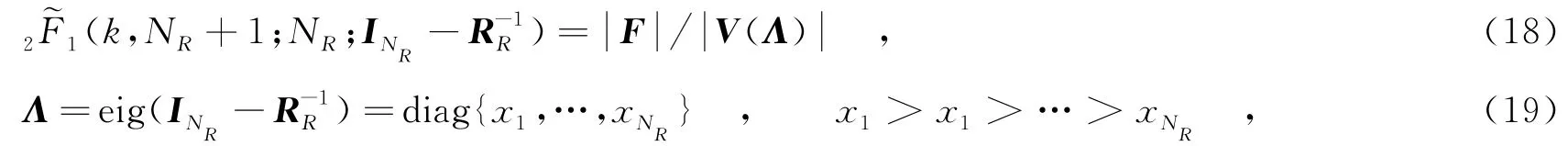
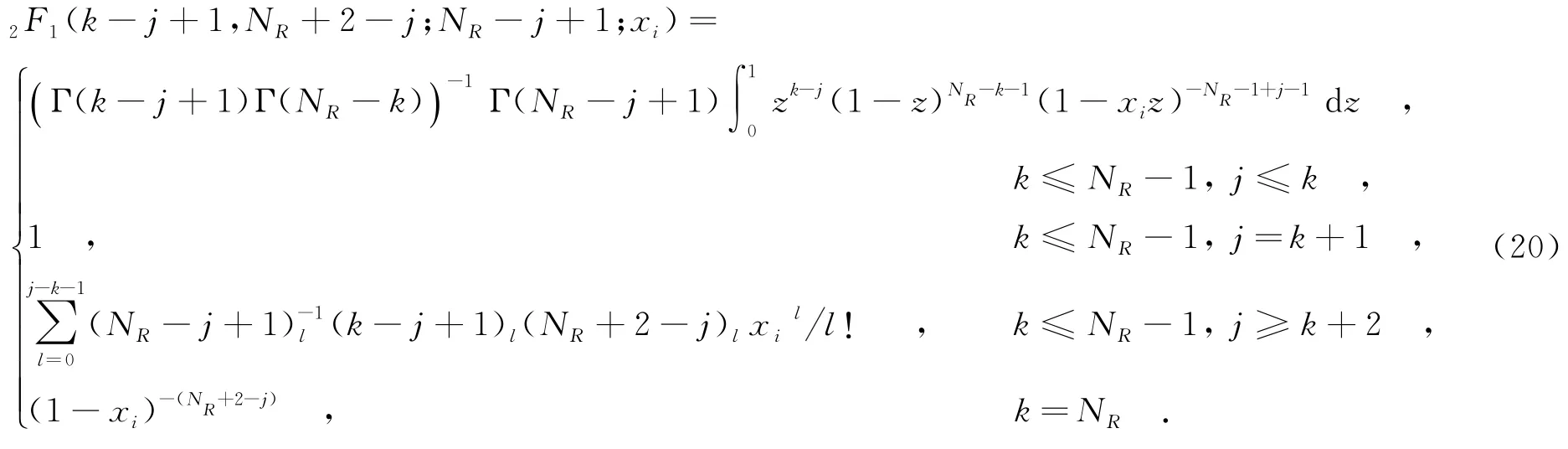
4　仿真试验

通过一组Monte-Carlo仿真来验证前文理论分析的正确性.首先,按式(2)和式(3)分别产生10 000组小尺度衰落矩阵H和大尺度衰落矩阵Ξ的实现.然后,按式(5)进行仿真以获得遍历容量.

前文已经说明,发送相关仅存在于同一节点的天线之间.因此有,其中RT,m描述第m个发送节点天线间的空域相关性.RT,m的i行j列元素,其中ρT,m=exp(-d),d表示相邻天线之间经由波长归一化后的距离.接收相关矩阵RR的i行j列元素{RR}i,j=.仿真试验中,取θT,m=0(m=1,…,L),θR=0[6-7].该设置与文献[7]中的相同.上述模型称为指数模型.

仿真试验中,大尺度衰落矩阵Ξ的参数设定为:μm=2 d B,σm=2 dB,D1=1 200 m,D2=1 500 m, D3=1 800 m.

仿真试验中,3组仿真结果分别在图1至图4中给出.

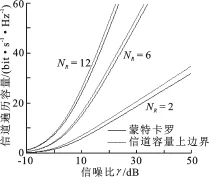
图1　Monte-Carlo仿真的遍历容量和上边界1

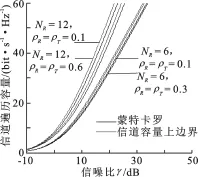
图2　Monte-Carlo仿真的遍历容量和上边界2

(1)在图1对应的仿真试验中,设定ρT,m=ρR=0.3.发送端天线数量L=3,NT=3.接收端天线数量分别取NR=2,NR=6,NR=12,它们分别对应NR＜NT,NT≤NR≤LNT,NR＞LNT的情况.

(2)在图2、图3对应的仿真试验中,取L=3,NT=3,NR=6,ρT,m=ρR=0.3/0.1.再取L=3,NT=3, NR=12,ρT,m=ρR=0.6/0.1,以验证不同接收端相关系数下遍历容量上边界的正确性.图3是图2的局部放大,两图具有相同的仿真设置,区别仅在于显示的信噪比范围不同.

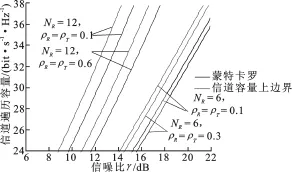
图3　Monte-Carlo仿真的遍历容量和上边界3

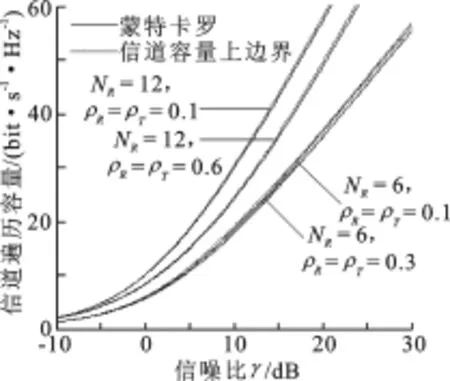
图4　Monte-Carlo仿真的遍历容量和上边界4

在图1至图4中,实线描述的是用Monte-Carlo方法得到的遍历容量;虚线描述的是文中在式(8)、(10)中给出的遍历容量上边界.从试验结果中可以看到,随着相关性的增加,信道容量相应降低,这对应了分集效率的降低.随天线数量增加,信道容量上升,这对应了分集效应的增强.从图1至图4可以看出,在各种情况下,容量上边界均非常接近遍历容量.从图4可以看出,当系统退化为空域双边相关Rayleigh衰落下的点对点MIMO时,即Ξ=I时,文中给出的上边界依然精确.从而验证了文中给出的遍历容量上边界的有效性.

5　结束语

对于空域双边相关同时存在时,Rayleigh/Lognormal衰落下分布式MIMO系统的遍历容量,文中给出了一个解析的上边界.当接收端天线数量大于或小于等于发送端时,在不同的收发端空域相关程度下,在低信噪比到高信噪比的全范围内,文中推导出的容量上边界均非常接近遍历容量.这一结论由仿真试验得以证实.当发送节点数量为1时,系统退化为点对点MIMO系统,容量上边界变为空域双边相关Rayleigh衰落下点对点MIMO系统的遍历容量上边界.此时,结果依然精确.

[1]TELATAR I E.Capacity of Multi-antenna Gaussian Channels[J].Europe Transactions on Telecommunication,1999, 10(6):585-595.

[2]庞继勇,李建东,杨克虎.相关信道下MIMO-OFDM系统的各态历经容量公式[J].西安电子科技大学学报,2006,33 (4):563-568. PANG Jinyong,LI Jiandong,YANG Kehu.ErgodicCapacity Formula for MIMO-OFDM Systems under Correlated Fading Channels[J].Journal of Xidian University,2006,33(4):563-568.

[3]BITHAS P S,RONTOGIANNIS A A.Mobile Communication Systems in the Presence of Fading/Shadowing,Noise and Interference[J].IEEE Transactions on Communications,2015,63(1):1-14.

[4]NAGESH K N,SATYANARAYANA D,MADHAVA P S,et al.Statistical Analysis of MIMO Scheme under Nakagami-m Fading Channels[C]//IEEE International Conference on Advanced Communication Technology.Piscataway:IEEE,2014: 255-259.

[5]ZHAO O,MURATA H,YOSHIDA S.Channel Capacity of Distributed MIMO Antenna Systems under the Effect of Spatially Correlated Shadowing[C]//IEEE 78th Vehicular Technology Conference.Piscataway:IEEE,2013:6692127.

[6]MATTHAIOU M,ZHONG C J,MCKAY M R,et al.Sum Rate Analysis of ZF Receivers in Distributed MIMO Systems[J].IEEE Journal on Selected Areas in Communications,2013,31(2):180-191.

[7]MATTHAIOU M,CHATZIDIAMANTIS N D,KARAGIANNIDIS G K.A New Lower Bound on the Ergodic Capacity of Distributed MIMO Systems[J].IEEE Signal Processing Letters,2011,18(4):227-230.

[8]PARK M,CHAE C E,HEATH,R W.Ergodic Capacity of Spatial Multiplexing MIMO Channels with Log-normal Shadowing and Rayleigh Fading[C]//IEEE International Symposium on Personal Indoor Mobile Radio Communications. Piscataway:IEEE,2007:375-379.

[9]LOVITT W V.Linear Integral Equations[M].New York:Dover,1950:24-25.

[10]KHATRI C G.On Certain Distribution Problems Based on Positive Definite Quadratic Functions in Normal Vectors[J]. The Annals of Mathematical Statistics,1966,37:468-479.

[11]ORLOV A Y.New Solvable Matrix Integrals[J].Acta Science of Mathematics,1997,63:383-395.

(编辑:王 瑞)

Upper bound on the ergodic capacity of D-MIMO systems in double-sidedcorrelated Rayleigh/Lognormal fading channels

WANG Yongping1,CAO Hanqiang1,WANG Anwen2
(1.School of Electronic Information and Communications,Huazhong Univ.of Science&Technology, Wuhan 430074,China;2.College of Science,Naval Univ.of Engineering,Wuhan 430033,China)

An analytical upper bound is presented for the ergodic capacity of distributed multiple-input multiple-output(D-MIMO)systems operating in Rayleigh/Lognormal fading with double-sided spatial correlation.A new inequality is constructed by sub-matrix expansion,and then the difficulty in averaging the channel eigen-statistics over the shadowing distribution is resolved.The proposed upper bound is applicable for the arbitrary number of receive and transmit antennas and remains tight over the entire Signalto-Noise regime.The validity of the conclusion is verified by compu-ter simulation.When the number of receive and transmit nodes is one,the lower bound reduces to the bound on the ergodic capacity of point to point MIMO systems operating in Rayleigh/Lognormal fading with double-sided spatial correlation.

communication systems;fading channels;MIMO;distributed system;ergodic capacity

TN928

A

1001-2400(2016)04-0111-06

10.3969/j.issn.1001-2400.2016.04.020

2015-03-31 网络出版时间：2015-10-21

王咏平(1975-),华中科技大学博士研究生,E-mail:wang__yongping@163.com.

网络出版地址：http://www.cnki.net/kcms/detail/61.1076.TN.20151021.1046.040.html