分布式MIMO雷达双门限GLRT CFAR检测
胡勤振,杨 芊,苏洪涛,周生华,刘子威,杨 阳
(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071; 2.空军装备部107办公室,北京 100038)
分布式MIMO雷达双门限GLRT CFAR检测
胡勤振1,杨 芊2,苏洪涛1,周生华1,刘子威1,杨 阳1
(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071; 2.空军装备部107办公室,北京 100038)
在分布式多输入多输出雷达目标检测中,为降低融合中心与局部雷达站之间的数据传输率,提出了一种双门限广义似然比恒虚警率检测算法.首先对局部广义似然比检验统计量进行第一门限判断,将过门限的局部检验统计量传送给融合中心.然后在融合中心进行融合检测,与第二门限比较得到判决结果.推导了双门限广义似然比检测器的虚警概率闭式解.仿真结果表明,双门限广义似然比检测算法在降低数据传输率的同时能保证较好的检测性能.
分布式多输入多输出雷达;恒虚警率;双门限检测;广义似然比
分布式多输入多输出(Multi-Input Multi-Output,MIMO)雷达利用目标的空间散射多样性得到空间分集增益,以提高目标的检测性能[1-7].在集中式检测算法中,各个雷达接收站需要将接收到的全部数据传输给融合中心,融合中心根据相应的判决准则对目标进行检测.然而对全部数据进行传输要求局部雷达站与融合中心之间具有较高的数据传输率,这无疑增加了系统的代价和成本.由于雷达接收的回波数据中,大部分为噪声和杂波信号,没有必要将所有的观测数据传送给融合中心,只需要将可能的目标信号数据进行传输即可.因此,各雷达接收站可以对观测数据进行预处理,减少无用数据的传输.
基于局部量化的分布式检测算法[8-9]能有效减少融合中心的计算复杂度,降低数据传输的通信带宽要求.但是这种量化结果包含的信息量较少,不能体现原始数据更多的信息特征,因此,检测性能较差.为了在传输率约束条件下得到更好的检测性能,文献[10-11]研究了在数据传输率和虚警概率约束条件下的最优检测算法,该方法的不足之处是当检验统计量的统计特性比较复杂时,计算复杂,并且很难给出闭式解;同时该方法不适用于当似然函数含有未知参数(如信噪比)的情况.为了提高检测算法的实时性和效率,在杂波和噪声功率已知的情况下,文献[12]提出了一种结构简单的双门限检测算法,给出了虚警概率和检测概率的闭式解,不足之处是需要先验的信噪比信息.在距离扩展目标检测中,针对信噪比差异导致的性能损失问题,文献[13]提出了一种基于消减积累的双门限恒虚警率(Constant False Alarm Rate,CFAR)检测算法.该算法不仅可以用于剔除低信噪比数据的扩展目标检测,也同样适用于分布式MIMO雷达的双门限检测.但是该算法第二门限的设置不能使检测性能达到最优.
在分布式MIMO雷达实际工程应用中,杂波和噪声功率以及信杂噪比(Signal to Clutter plus Noise Ratio,SCNR)等信息往往是未知的.由于各雷达站到杂波源的距离不同,观测杂波源的角度也不同,因此,各个空间分集通道的杂波特性也不同.同时,也需要一种结构简单效率高的检测器.针对以上问题,笔者重点研究分布式MIMO雷达中的双门限广义似然比(Double-Threshold Generalized Likelihood Ratio Test, DT-GLRT)CFAR检测方法.各个局部雷达站首先采用GLRT算法进行第一门限检测,并将超过第一门限的局部GLRT传送到融合中心.融合中心计算融合后的GLRT并与第二门限比较,得到最终的判决结果.第一门限由数据传输率约束确定,在雷达系统中,数据传输率约束可近似由局部虚警概率约束表示.笔者推导了DT-GLRT检测器虚警概率的解析表达式,并进行了仿真验证,最后对检测算法的性能进行了仿真分析.
1 信号模型
假设分布式MIMO雷达有Nt个发射天线和Nr个接收天线,则可以得到N=NtNr个统计独立的空间分集通道.在第i(i=1,2,…,N)个空间分集通道中,检测单元信号表示为xi(0)∈CL×1;检测单元附近的K个参考单元信号表示为xi(k)∈CL×1(k=1,2,…,K).在同一空间分集通道中,检测单元中的杂波加噪声矢量与参考单元中的杂波加噪声矢量之间统计独立且分布相同.而在不同空间分集通道中,杂波加噪声矢量统计独立但分布不同.分布式MIMO雷达检测可以描述为如下二元假设检测:

其中,ni(k)∈CL×1(k=0,1,…,K),ni(k)是均值为0、协方差矩阵为Mi的复高斯随机矢量,且相互统计独立;si为和多普勒频率fi有关的目标信号矢量;βi为未知的目标信号复幅度.假设目标服从Swerling-I起伏模型.
在二维笛卡尔坐标系中,以待检测目标作为原点,假设目标沿x方向和y方向的速度分别为vx和vy,发射天线和接收天线相对目标的空间角度分别为φt,u(u=1,2,…,Nt)和φr,l(l=1,2,…,Nr),则第i个空间分集通道观测的目标多普勒频率为
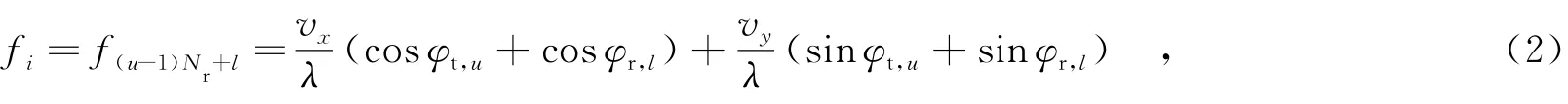
其中,λ为载波波长.目标信号矢量表示为

其中,T为脉冲重复时间.第i个空间分集通道的SCNR定义为

[6-7],各空间分集通道的log-GLRT局部检验统计量表示为


文中所提出的DT-GLRT检测算法如图1所示,其中虚线表示不传输数据,实线表示传输数据.首先对每个局部GLRT检验统计量qi与设定的第一门限η1比较,将低于门限的通道数据剔除,只传输过第一门限的局部检验统计量.第一门限η1的设置与局部虚警概率Pfa1的关系为


图1 DT-GLRT算法流程图
其中,fqi(q|H0)为qi的条件概率密度函数.经过第一门限比较,假设剩余m0=0,1,…,N个有效通道数据:q(m),m=1,2,…,m0.然后融合中心接收到局部检验统计量,融合得到全局检验统计量,与第二门限比较,得到最终判决.在融合中心,其融合准则是将m0个有效通道数据进行非相干积累,因此,融合中心的判决准则可以表示为

可以看出,当第一门限η1=0时,DT-GLRT检测器与传统的集中式GLRT检测器等价.
在雷达信号处理中,数据传输率定义为每秒中传输的数据量,单位是比特/秒(bit/s).假设系统的采样频率为FsHz,采样量化位数为M bit.在集中式检测算法中,可以计算出每个空间分集通道的数据传输率为MFsbit/s.通过设置第一门限可以有效控制数据的传输量.由于在各空间分集通道的回波数据中,大部分为杂波和噪声信号,而且为了保证足够的信息量,第一门限的取值一般较小,因此,可以认为传输的数据传输量近似为虚警点数.这样,经过第一门限处理后,每个空间分集通道的数据传输率约为MFsPfa1bit/s.此时, DT-GLRT检测算法需要的数据传输率仅为集中式检测算法的D=Pfa1×100%.
2 DT-GLRT 算法虚警概率计算
在H0假设下,qi服从独立同分布的指数分布[6-7],其概率密度函数为
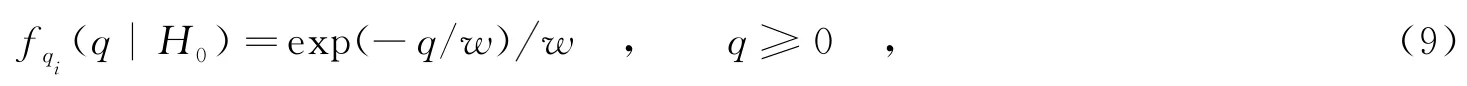
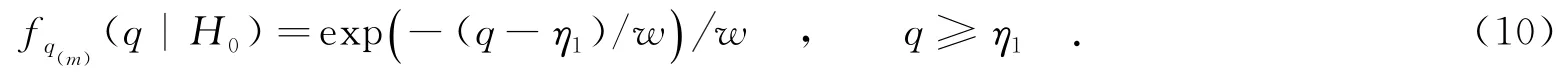
因此,Pfa1=exp(-η1/w).定义变量em=q(m)-η1,则em服从指数分布,其概率密度函数表示为
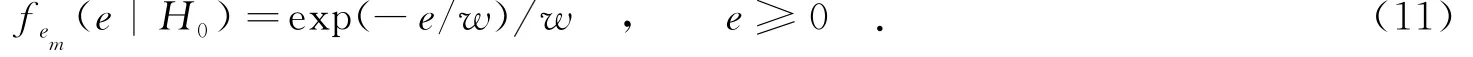
对于DT-GLRT,在有效通道数m0给定的条件下,yDT-GLRT超过第二门限的条件概率为
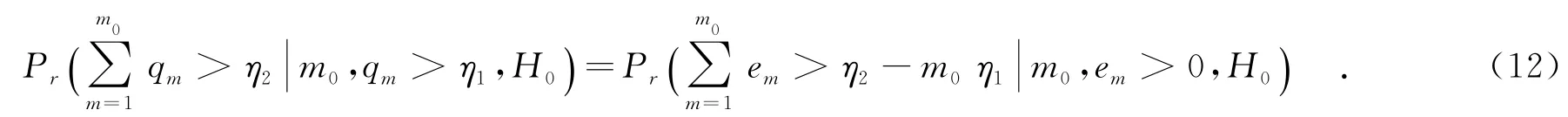
在实际中,有效通道数m0为一随机变量,其取值范围为m0=0,1,…,N.其概率分布函数可以表示为
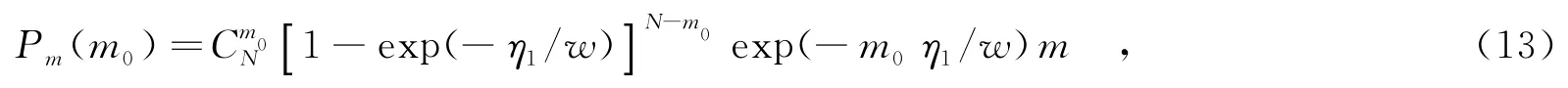



最后,得到全局虚警概率显式表达式为
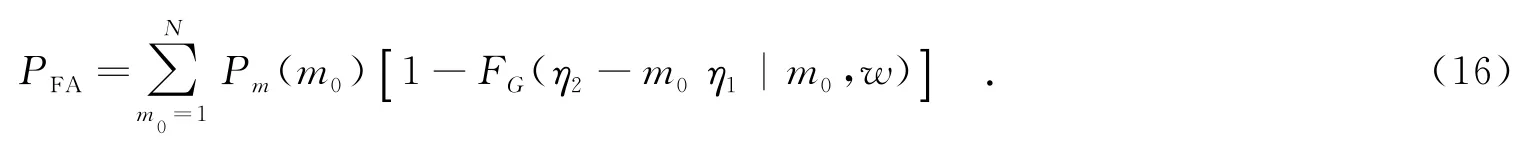
从虚警概率的显式表达式可以看出,虚警概率只与信号矢量维数、参考单元个数、空间分集通道个数以及两个门限有关,与背景杂波加噪声功率无关,因此,具有恒虚警特性.在η2≤η1范围内,对于m0=0,1,…, N,恒有FG(η2-m0η1|m0,w)=0,因此,虚警概率保持恒定值PFA=1-Pm(0).此时,第二门限不起作用,只要有局部通道数据传送给融合中心,则判为有目标存在.因为无法求得检测概率的闭式解,笔者将通过蒙特卡罗仿真得到检测概率.
3 仿真分析
下面将通过蒙特卡罗仿真验证所得虚警概率解析表达式的正确性.因为难以得到DT-GLRT算法的检测概率闭式解,因此,利用蒙特卡罗仿真得到检测性能.并与传统的GLRT检测算法和分布式检测算法进行比较,证明所提算法的有效性.
仿真参数如下:分布式MIMO雷达系统有Nt=2个发射站和Nr=4个接收站,因此,空间分集通道数N =8.雷达的脉冲重复时间T=2.5 ms,载波波长λ=0.3 m.信号矢量长度L=8,参考单元数目K=16,各空间分集通道杂波加噪声协方差矩阵相同且为Mi=IL×L.发射天线和接收天线相对目标的空间角度分别[0°, 30°]和[0°,30°,60°,90°].待检测目标的速度vx=30 m/s和vy=0 m/s.全局虚警概率设置为PFA=10-4.
图2比较了由式(16)和通过蒙特卡罗仿真得到的DT-GLRT检测器虚警概率和检测门限之间的关系.蒙特卡罗次数为106次,第一门限η1的取值分别为4和6.从图2中可以看出,蒙特卡罗仿真结果与计算结果相吻合,因此,可以证明理论推导的正确性.在设置的参数下,根据式(13),Pm(0)的取值分别为0.358 6和0.711.从图2还可以看出,在η2≤η1时,虚警概率保持恒定值PFA=1-Pm(0).此时,第二门限不起作用,只要有局部通道数据传送给融合中心,则判为有目标存在.其他参数下可以得到相同的结果,因此,可以证明理论推导的正确性.

图2 DT-GLRT全局虚警概率与检测门限的关系

图3 D与第一门限的关系
图3给出了D与第一门限的关系,可以看出,随着第一门限的增加,与集中式检测算法相比,DT-GLRT检测算法需要数据传输率明显降低.因此,通过提高第一门限,可以有效降低数据量的传输.图4给出不同检测器的检测性能随通道SCNR的变化情况.蒙特卡罗次数为104次,各空间分集通道的SCNR相同,横坐标SCNR代表的是单通道信杂噪比,局部虚警概率分别取10-1和10-2.可以看出,文中提出的DT-GLRT检测器的检测性能要优于文献[13]中提出的DH-GLRT检测器的,两种双门限检测器的检测性能优于分布式检测中的“OR”准则检测器.在局部虚警概率为10-1时,DT-GLRT的检测性能接近GLRT的检测性能,而DH-GLRT的检测性能差于分布式检测中的“3 out of 8”准则检测器的.DH-GLRT检测器性能较差的原因是该检测器第二门限的设置不能使检测性能达到最优.
图5给出了DT-GLRT和DH-GLRT的检测性能与第一门限的关系.图5中,GLRT检测器与第一门限无关.在图5(a)中,各空间分集通道的SCNR相同,并设置为10 dB.在图5(b)中,各通道SCNR之比设置为[1 1 1 0 0 0 0 0],前3个通道SCNR设置为15 d B.可以看出,在各通道信杂噪比相同时,DT-GLRT的检测性能要优于DH-GLRT的.在第一门限较低时,DT-GLRT的检测性接近于GLRT的检测性能. DH-GLRT的检测性能随第一门限的增加迅速下降.在各通道信杂噪比有差异时,随着第一门限的增加,DH-GLRT的检测性能要优于DTGLRT的,随后DT-GLRT的检测性能优于DH-GLRT;同时,两种双门限检测算法都有比较小的性能损失,原因是第一门限的设置可以剔除低信杂噪比通道,一定程度上改善了检测性能.
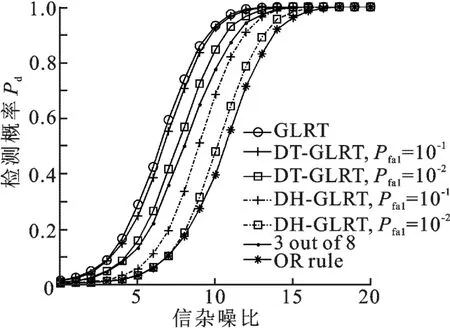
图4 检测性能随信杂噪比的变化
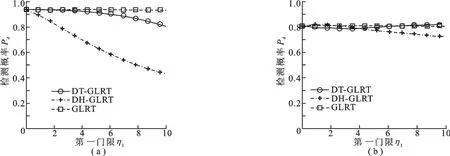
图5 检测性能随第一门限的变化
4 结 语
针对分布式MIMO雷达中大量的数据传输问题,在杂波加噪声功率以及信杂噪比未知的条件下,笔者研究了一种双门限广义似然比DT-GLRT CFAR检测算法.推导了虚警概率的解析表达式,并进行了仿真验证.通过各个检测器的检测性能比较,可以看出,在各空间分集通道信杂噪比差异较小或较大两种情况下, DT-GLRT在降低数据传输量的同时能保证较好的检测性能.所提检测算法在实际工程应用中具有重要意义.
[1]ZHOU S H,LIU H W.Space-partition-based Target Detection for Distributed MIMO Radar[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(4):2717-2729.
[2]FRANKFORD M T,STEWART K B,MAJUREC N,et al.Numerical and Experimental Studies of Target Detection with MIMO Radar[J].IEEE Transactions on Aerospace and Electronic Systems,2014,50(2):1569-1577.
[3]RADMARD M,CHITGARHA M M,MAJD M N,et al.Antenna Placement and Power Allocation Optimization in MIMO Detection[J].IEEE Transactions on Aerospace and Electronic Systems,2014,50(2):1468-1478.
[4]周生华,刘宏伟,刘保昌,等.信噪比加权的空间分集雷达目标检测算法[J].西安电子科技大学学报,2011,38(3): 82-88. ZHOU Shenghua,LIU Hongwei,LIU Baochang,et al.SNR Weighting Based Target Detection Algorithm for Spatial Diversity Radar[J].Journal of Xidian University,2011,38(3):82-88.
[5]LIU H W,ZHOU S H,SU H T,et al.Detection Performance of Spatial-frequency Diversity MIMO Radar[J].IEEE Transactions on Aerospace and Electronic Systems,2014,50(4):3137-3155.
[6]LIU J,ZHANG Z J,CAO Y H,et al.A Closed-form Expression for False Alarm Rate of Adaptive MIMO-GLRT Detector with Distributed MIMO Radar[J].Signal Processing,2013,93(9):2771-2776.
[7]ZHOU S H,LIU H W.Signal Fusion-based Target Detection Algorithm for Spatial Diversity Radar[J].IET Radar, Sonar&Navigation,2011,5(3):204-214.
[8]VARSHNEY P K.Distributed Detection and Data Fusion[M].New York:Springer-Verlag,1997.
[9]AZIZ A M.A New Adaptive Decentralized Soft Decision Combining Rule for Distributed Sensor Systems with Data Fusion[J].Information Sciences,2014,256(1):197-210.
[10]APPADWEDULA S,VEERAVALLI V V,JONES D L.Decentralized Detection with Censoring Sensors[J].IEEE Transactions on Signal Processing,2008,56(4):1362-1373.
[11]HE H,VARSHNEY P K.Distributed Detection with Censoring Sensors under Dependent Observations[C]// Proceedings of the IEEE International Conference on Acoustic,Speech and Signal Processing.Piscataway:IEEE,2014: 5055-5059.
[12]SCHARRENBROICH M,ZATMAN M,BALAN R.Cooperative Radar Techniques:the Two-step Detector[C]// Conference Record of the 45th Asilomar Conference on Signals,Systems and Computers.Piscataway:IEEE,2011: 1975-1979.
[13]顾新峰,简涛,何友.距离扩展目标的双门限恒虚警检测器及性能分析[J].电子与信息学报,2012,34(6): 1318-1323. GU Xinfeng,JIAN Tao,HE You.Double Threshold CFAR Detector of Range-spread Target and Its Performance Analysis[J].Journal of Electronics and Information Technology,2012,34(6):1318-1323.
(编辑:李恩科)
Double-threshold GLRT CFAR detection in distributed MIMO radar
HU Qinzhen1,YANG Qian2,SU Hongtao1,ZHOU Shenghua1, LIU Ziwei1,YANG Yang1
(1.National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China; 2.The 107 Office of Airforce Equipment Department,Beijing 100038,China)
To decrease the data transmission rate between fusion center and local radar stations for target detection in distributed multi-input multi-output(MIMO)radar,a double-threshold generalized likelihood ratio test(DT-GLRT)constant false alarm rate algorithm is proposed.Firstly,local GLRT test statistics are censored through the first threshold and the over-threshold local test statistics are transferred to the fusion center.Secondly,the transferred data are fused to decide the target presence according to the second threshold in the fusion center.The closed-form expression for the probability of false alarm of the DTGLRT is derived.Simulation results demonstrate that the proposed DT-GLRT algorithm can maintain good detection performance with a low data transmission rate.
distributed MIMO radar;constant false alarm rate;double-threshold detection;generalized likelihood ratio test
TN957.51
A
1001-2400(2016)04-0029-05
10.3969/j.issn.1001-2400.2016.04.006
2015-04-22 网络出版时间:2015-10-21
国家自然科学基金资助项目(61372134,61401329)
胡勤振(1988-),男,西安电子科技大学博士研究生,E-mail:huqinzhen8@163.com.
苏洪涛(1974-),男,教授,E-mail:suht@xidian.edu.cn.
网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151021.1046.012.html

