粗糙目标光外差信号特性对探测阈值的影响
党文佳,曾晓东,来 志,冯喆珺,曹长庆,霍燿炜
(西安电子科技大学物理与光电工程学院,陕西西安 710071)
粗糙目标光外差信号特性对探测阈值的影响
党文佳,曾晓东,来 志,冯喆珺,曹长庆,霍燿炜
(西安电子科技大学物理与光电工程学院,陕西西安 710071)
传统目标回波光外差探测使用高斯分布等简单模型来描述,这常常导致判决误差.笔者提出利用多项式对实际目标测量数据进行拟合,给出较准确的概率分布曲线.通过对某装甲车表面样块多组测量数据的统计分析显示,利用多项式拟合来确定判决阈值,比起用简单的高斯分布来确定阈值,可以获得更高的检测概率和更低的误警概率.研究表明,对实测中频信号的统计直方图进行多项式拟合,有利于精确设置探测阈值,可以使检测概率提高6.02%,误警概率降低7.7%.文中结果为粗糙面回波外差探测系统设计提供定量参考,也为探测系统性能评估仿真提供依据.
光外差探测;统计特性;高斯分布;探测阈值;检测概率;误警概率
对于实际相干型激光探测系统,因为激光波长在微米量级,实际目标大多是粗糙的.目标上不同位置回波的相位延迟不同,导致与本振光波前失配,大大降低了光外差探测效率.这种粗糙表面对回波波前的调制,会发生随机起伏,这对信号来说相当于一种随机干扰.不同材料、不同表面粗糙度的目标,这种调制效应不同.在实际应用中,光外差探测技术是以复杂的技术代价去换取高的探测信噪比.为了能够从混杂着干扰的回波中正确解调出目标信息[9],必须对这种随机干扰的统计特性有准确的了解.譬如,对于二进制激光预警雷达,通过检测回波外差信号的有无,判断是否存在目标.由于回波信号比较微弱,光场及探测过程的随机性就显露出来,加之外界干扰,使得对回波信号发生误判.特别是各种实际目标对光波来说,其表面均属粗糙面,引起强烈的退相干效应[10],更加剧了回波外差信号的随机性.因此,增大检测概率或减小误判概率的核心问题就是对回波信号的统计特性有深刻的了解,正确设置判决阈值,以提高正确预警概率.
对于粗糙目标回波外差信号的统计特性人们做过许多研究[11],一般是在独立假设(目标表面各处的起伏独立)之下进行分析.理论和实验均表明,独立假设获得的结果与实际数据在定量上并不吻合,常常给判决带来误差.由于实际目标的复杂性,回波外差信号的统计模型很难给出解析结果,通常用一些简单的模型来近似表达.但这些简单的模型如高斯分布、瑞利分布等对实际工程很难给出满意的指导.所以实际工程中必须根据实验数据拟合出回波外差信号的统计分布.
笔者提出一种多项式拟合技术,对于感兴趣的目标根据实测数据,拟合出目标回波的统计分布,以准确地确定判决阈值,并通过多组实际测量值的统计分析,比较了正确判决对雷达性能的改善,为实际工程中准确设定激光雷达判决阈值提供一种有效的方法.
1 理论分析
1.1统计判决理论
二进制雷达的基本任务是发现目标并确定其坐标和径向速度.通常目标回波中总是混杂着各类噪声和干扰,这对光外差检测提出难题.从统计学观点来说,雷达检测问题就是典型的统计判决问题.对接收到的实际测量值,归结为用检测信号来检验如下两个假设:

其中,x是检测信号,n是噪声信号,s是有用的回波信号,H0代表噪声的概率分布,H1代表检测到的混杂着噪声的信号的概率分布.通常系统需设置一个阈值xT,当x>xT时,就认为有回波信号;而当x<xT时,则认为没有回波信号.按照统计学的“实际判断原理”,阈值的设置应满足:当x<xT时,
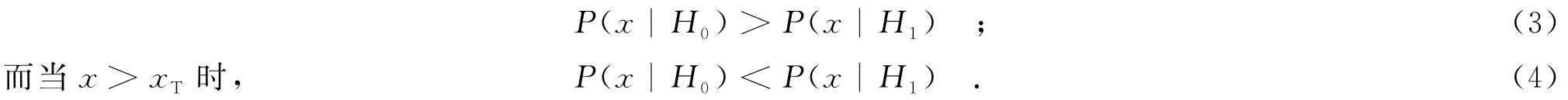
如果已知概率分布P(x|H)和P(x|H1),由式(3)和式(4)就可以确定出阈值xT.P(x|H0)和P(x| H1)的概率分布均根据光外差实验获得.从式(3)和式(4)可知,阈值的正确设定强烈地依赖于回波信号的统计特性,如果对信号的统计分布理解不准确,计算出来的判决阈值就会有所差异,导致检测概率和误警概率变化.
步骤6 一次迭代完成,判断是否达到最大迭代次数gmax,若达到则输出最优解,即得到最优调度作业顺序,否则返回步骤2。
1.2粗糙目标光外差探测理论
不考虑光路中其他因素对本振光和信号光振幅和初相位的影响,以及大气传输和光学系统引起的误差,只考虑粗糙目标表面轮廓起伏造成的回波相位抖动对中频电流的影响.假设本振光与发射的信号光都是均匀平面波,且同方向偏振,则本振光场和回波信号光场可表示为

其中,φs(r)表示由于目标表面起伏引起的回波波前抖动,使用Phase View DWC1000数字波前分析仪,在探测器光敏面处对其进行测量,如图1(b)所示.
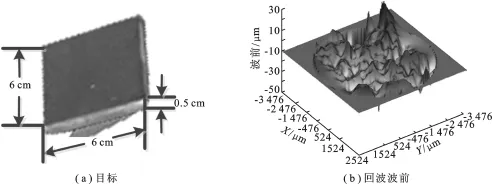
图1 某装甲车表面涂覆样块回波波前
图1(a)是某装甲车表面涂覆样块,目标尺寸为6 cm×6 cm×0.5 cm.这一目标对光波来说已足够粗糙,当激光照射目标表面时,回波的波前不再是理想的平面,会发生畸变,如图1(b)所示.此时,接收到的光外差信号可表示为

其中,Δω=ωs-ωl,为中频频率,Ω是探测器的面积,R为探测器响应度.由于φs(r)为随机变量,所以中频信号iIF(t)也是随机的.
假设粗糙目标表面的高度随机起伏为h(x,y),那么,信号光回波相位可以表示为

此时,光外差中频电流为

式(9)右端被积函数表示光电探测器上d x d y面元产生的中频光电流.如果目标不同位置的波前起伏φs(x, y)是相互独立的,则按中心极限定理iIF(t)应该服从高斯分布,而不论h(x,y)是什么分布.但通常物体表面各处的起伏并非独立的随机变量[12],这会导致光外差信号的统计特性偏离高斯分布.因此,准确了解iIF(t)的分布规律,给出较为精确的表达式,对于合理设计脉冲二进制雷达信号的判决阈值、提高光外差探测的信噪比至关重要.
2 光外差信号测量与统计分析
式(9)表明光外差信号是随机变量h(x,y)的泛函数,寻求iIF(t)的概率分布归结为大量随机变量和的渐近分布问题.因为不同位置处h(x,y)并不独立,因此,iIF(t)的分布依赖于目标表面轮廓h(x,y)的相关性,通常给出iIF(t)的概率分布十分困难,一个可行的方法是统计分析实验数据,对其进行拟合.因此,在实验室内设计如图2所示的系统进行测量.实验中使用图1(a)目标,距离探测器3.0 m,目标和探测器位置保持不变,随机移动激光照射在目标上的位置,记录1 000组光外差信号数据.
在图2中,采用Coherent公司的波长为532 nm的Verdi-Ⅱ激光器,线宽5 MHz,光束直径2.25 mm±10%,发散角小于0.5 mrad;采用光敏面直径为0.5 mm的PIN型光电二极管探测器;使用调制频率为100 MHz的TSGMN-3/Q型声光调制器.在实验时,信号光和本振光功率均使用Coherent 3 SIGMA光功率计在探测器位置处测得,信号光功率为0.05 m W,本振光功率为1.05 m W,照射激光功率为0.8 W,放大器增益为60 dB.测量结果如图3直方图[13]所示.
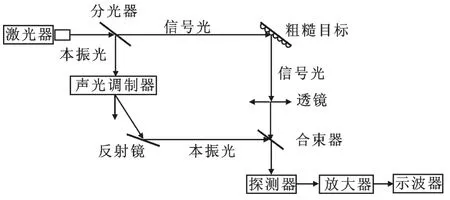
图2 光外差探测系统装置示意图
图3中的直方图是实验获得的光外差信号统计结果.可以看出,直方图在大幅值方向有较长拖尾,对称性差,已偏离了高斯分布.信号的统计特性对于信号处理过程至关重要.譬如,二进制雷达信号的检测问题.如何设置阈值电平,使检出概率尽可能大,并使误警概率尽可能小,都与探测阈值的设置直接相关,因此,必须准确地了解回波信号的统计特性.但给出真实概率分布的函数表达式几乎不可能,在工程应用中可对直方图数据做多项式拟合,获得概率分布的近似表达式,然后再进行信号处理.
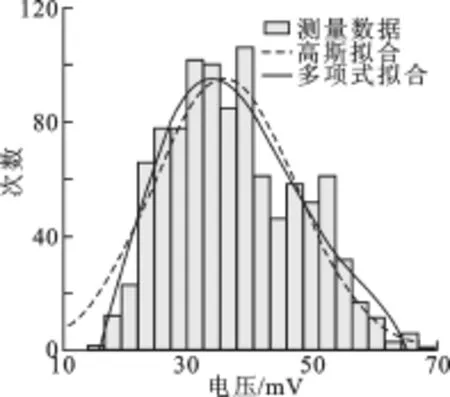
图3 光外差信号统计分布拟合图
3 探测阈值设置分析
由于目标表面回波的统计特性不一定服从高斯分布,在探测阈值设置时,如果把它当成高斯分布来计算就会产生明显误差.对光外差信号实测数据统计直方图分别做高斯拟合和多项式拟合,如图3所示.高斯拟合曲线记为s1,多项式拟合曲线记为s2.

对应的系数矩阵a=[95.40,36.02,16.19].
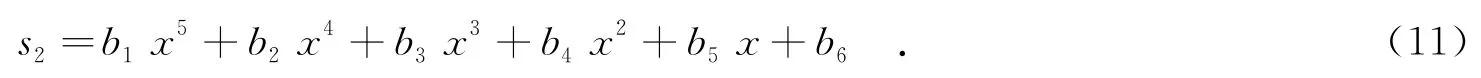
对应的系数矩阵b=[-8.22×10-6,0.001,-0.12,4.30,-57.08,236.89].对于概率分布函数,高斯函数有2个自由度,而五阶多项式有5个自由度,因此,可以获得更高的拟合精度.不同粗糙目标,表面起伏不同,拟合参数也会不同,具体参数设置,由实测信号统计分布决定.
由图3可以看出,使用五阶多项式对光外差信号统计分布拟合精度更高.在相同背景噪声下,不妨假设信噪比为1∶1,背景噪声也是高斯噪声.下面分别计算信号光服从高斯分布和非高斯(多项式)分布时的探测阈值xT.
(1)如果认为回波外差信号服从高斯分布,则要检验如下假设:

因为信号和噪声是相互独立的,所以在H1假设下,x的分布应为s1和s1分布的卷积.由式(3)和式(4)可以计算出xT1=50.2,如图4所示.

图4 高斯信号阈值为50.2

图5 非高斯信号阈值为50.6

同样,信号与噪声独立,在H1假设下,x的分布应为s1和s2分布的卷积.由式(3)和式(4)可以计算出xT2=50.6,如图5所示.
(2)如果认为回波外差信号服从非高斯信号(多项式)分布,则要检验如下假设:
在图4和图5中,虚线代表噪声的概率分布,实线代表实测信号的概率分布,虚线和实线的交点即为阈值xT.检测概率对应图中PD面积,虚警概率对应PFA面积,漏警概率对应PM面积,误警概率是虚警概率和漏警概率之和,即为PFA+PM.使用Matlab计算对应的面积积分,就可以得到具体数值.两种分布计算数据如表1所示.

表1 高斯分布和非高斯分布计算数据比较
表1数据充分说明,把回波信号看作不同的分布,计算出的阈值不同.如果把粗糙目标回波光外差信号当做高斯分布来设置阈值,会使检测概率降低6.02%,误警概率增大7.7%,这对预警雷达是很严重的后果.不同粗糙目标,表面起伏不同,计算出的探测阈值、检测概率和误警概率将会不同,因此,准确描述粗糙目标光外差信号的统计分布规律,对正确设置阈值,提高检测概率意义重大.
4 结 论
粗糙目标回波光外差信号一般并不服从高斯分布,只有目标表面起伏相互独立时,才服从高斯分布.笔者研究了某装甲车表面涂覆样块光外差信号统计分布规律,如果用光外差信号拟合多项式作为分布函数来设置阈值,会使检测概率提高6.02%,误警概率减小7.7%,这对正确设置探测阈值,提高检测概率以及预警雷达实际应用有非常重要的意义.对于目标回波外差信号统计特性的深入研究和准确描述,为探索定量描述粗糙目标回波的退相干效应奠定了基础,也为提高光外差探测效率、合理设计相干激光雷达及SAL光学系统和信号处理系统提供重要的理论依据.
[1]BASHKANSY M,LUCKE R L,FUNK E,et al.Demonstration of Synthetic Aperture Imaging in the Optical Domain [J].Applied Optics,2002,27(22):1983-1985.
[2]SUN Z W,SUN J F,HOU P P,et al.Lensless Optical Image Processing Based on Two-dimensional Fresnel Diffraction for Synthetic-aperture Imaging Ladar[J].Applied Optics,2015,54(4):627-635.
[3]BARBER Z W,DAHL J R.Synthetic Aperture Ladar Imaging Demonstrations and Information at Very Low Return Levels[J].Applied Optics,2014,53(24):5531-5537.
[4]VENABLEⅢS M,DUNCAN B D,DIERKING M P,et al.Demonstrated Resolution Enhancement Capability of a Stripmap Holographic Aperture Ladar System[J].Applied Optics,2012,51(22):5531-5542.
[5]SUN Z W,HOU P P,ZHI Y N,et al.Optical Image Processing for Synthetic-aperture Imaging Ladar Based on Twodimensional Fourier Transform[J].Applied Optics,2014,53(9):1846-1855.
[6]LIU L R.Coherent and Incoherent Synthetic-aperture Imaging Ladar and Laboratory-space Experimental Demonstrations [J].Applied Optics,2013,52(4):579-599.
[7]DIERKING M P,DUNCAN B D.Periodic,Pseudoniose Wavefroms for Multifunction Coherent Ladar[J].Applied Optics,2010,49(10):1909-1922.
[8]LIU F C,SUN J F,MA X P,et al.New Coherent Laser Communication Detection Scheme Based on Channel-switching Method[J].Applied Optics,2015,54(10):2738-2746.
[9]吴亿峰,王彤,吴建新.转发式干扰环境中的机载雷达运动目标检测[J].西安电子科技大学学报,2014,41(6): 59-66. WU Yifeng,WANG Tong,WU Jianxin.Moving Target Detection for Airbome Radar under Repeater Jamming Environment[J].Journal of Xidian University,2014,41(6):59-66.
[10]党文佳,曾晓东,冯喆珺.目标粗糙对合成孔径激光雷达回波的退相干效应[J].物理学报,2013,62(2):024204. DANG Wenjia,ZENG Xiaodong,FENG Zhejun.Decoherence Effect of Target Roughness in Synthetic Aperture Ladar [J].Acta Physica Sinca,2013,62(2):024204.
[11]GOODMAN J W.光学中的散斑现象——理论与应用[M].曹其志,陈家碧,译.北京:科学出版社,2009:220-231.
[12]郭立新,王蕊,吴振森.随机粗糙面散射的基本理论与方法[M].北京:科学出版社,2010:1-8.
[13]余旺盛,田孝华,侯志强,等.一种改进的二次型直方图距离度量[J].西安电子科技大学学报,2015,42(3):178-185. YU Wangsheng,TIAN Xiaohua,HOU Zhiqiang,et al.Improved Quadratic-form Metric for Histogram Distance Measurement[J].Journal of Xidian University,2015,42(3):178-185.
(编辑:李恩科)
Effect of properties from a rough target echo signal on the detection threshold in optical heterodyne detection
DANG Wenjia,ZENG Xiaodong,LAI Zhi,FENG Zhejun,CAO Changqing,HUO Yaowei
(School of Physics and Optoelectronic Engineering,Xidian Univ.,Xi’an 710071,China)
Traditionally,a simple model,such as Gaussian distribution,describes the optical heterodyne detection echo signal of the target,which often leads to judgment errors.In this paper,we present a more accurate method to describe the probability distribution of the echo signal by use of polynomial fitting.The echo signals from a surface coating specimen of an armored car are measured,with the statistical analysis showing that the probability of detection is higher and the probability of false alarm is lower,when using the method of polynomial fitting to determine the decision threshold,rather than using a simple Gaussian distribution to determine it.The results show that by the method of polynomial fitting on the statistical histogram of the measured intermediate frequency signal,the precision of setting the detection threshold will be improved,and that the probability of detection rises by 6.02%and the probability of false alarm falls by 7.7%.The results of this paper provide a quantitative reference for designing the rough surface echo heterodyne detection system and also provide a useful tool for evaluating the performance of the heterodyne detection system.
optical heterodyne detection;statistical properties;Gaussian distribution;detection threshold;probability of detection;probability of false alarm
TN957.51;TN958
A
1001-2400(2016)04-0057-06
10.3969/j.issn.1001-2400.2016.04.011
2015-06-09 网络出版时间:2015-10-21
国家自然科学基金资助项目(61378079)
党文佳(1983-),女,西安电子科技大学博士研究生,E-mail:wenjia_dang@126.com.
网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151021.1046.022.html

