三维复合势下的玻色-爱因斯坦凝聚暗孤子结构及操控*
沈森挺, 宗丰德, 王海红
(浙江师范大学 非线性物理研究所,浙江 金华 321004)
三维复合势下的玻色-爱因斯坦凝聚暗孤子结构及操控*
沈森挺, 宗丰德, 王海红
(浙江师范大学 非线性物理研究所,浙江 金华 321004)
基于二维抛物势、一维光晶格势和二维高斯势所组成的复合势,讨论了一个具有层状结构并带有增益的三维玻色-爱因斯坦凝聚暗孤子结构.应用能量泛函和直接数值仿真,得到了暗孤子结构在关键参量空间中的稳定性区域,并分析了暗孤子结构的动力学性质.结果发现:在线性增益的作用下,暗孤子结构的振幅和脉宽实现了同步变化,这为通过增益调制来控制物质波孤子的动力学行为提供了一种思路.而且,对不同原子数比例下的暗孤子结构的中心位置进行了成功操控,这将对量子信息的存储和处理起到一定的理论指导作用.
玻色-爱因斯坦凝聚;Gross-Pitaevskii方程;暗孤子;操控
0 引 言
在玻色-爱因斯坦凝聚的实验实现及理论探究中,外势起着十分关键的作用,尤其是抛物势[1-3]、高斯势[4-5]和光晶格势[6-8].在抛物势中,对物质波孤子的研究集中在明孤子[1]、暗孤子[2]和矢量孤子[3]等不同的类型;在高斯势中,主要集中于涡旋孤子[4]和暗孤子[5];而在光晶格势中,则对明孤子[6]、涡旋孤子[7]和Gap孤子[8]有较多的研究.可以看出,抛物势和高斯势在暗孤子的构造方面作用显著.但是采用抛物势、高斯势和光晶格势所组成的联合外势来构造特定结构的暗孤子的方法到目前为止还没有被报道,尤其是暗孤子结构.同时考虑到高斯势可以通过向玻色-爱因斯坦凝聚的中心照射一束蓝调制激光来实现[9],而光晶格势可以通过正交偏振相对传播的激光束来实现[10].考虑到由二维抛物势、一维光晶格势和二维高斯势组成的复合外势是圆柱对称结构及每个晶格扁平形状,本文讨论了一个三维玻色-爱因斯坦凝聚层状暗孤子结构.
除了可以用外势来构造暗孤子外,还有很多其他产生暗孤子的方法.其中,最常见的是相位注入法[11],通过一束远失谐激光将偶极势作用到玻色-爱因斯坦凝聚上,使其局部增加一个额外的相位,从而产生排斥力将原子分开,产生暗孤子.另外一种常用的方法是密度调制[12],在进行状态转换之后,移除节点平面上的原子,从而得到暗孤子.此外还有像超音速流[13]等方法.另一方面,暗孤子的动力学和稳定性一直以来都是学者研究的焦点,主要集中在对几种常见的暗孤子结构的动力学分析上,包括Theocharis等[14]提出的特殊环形结构的暗孤子,受到广泛关注的暗孤子链结构[15-16],以及最近开始受到重视的三维球壳形暗孤子结构[17].其中在对暗孤子链结构的探究方面,Hoefer等[15]通过让两组分玻色-爱因斯坦凝聚在窄小的通道内快速对流的方法,实验上观察到了由于调制不稳定所产生的暗孤子链结构;Achilleos等[16]通过利用玻色-爱因斯坦凝聚内部的非线性及旋转轨道能谱的性质得到了密度不断振动的暗孤子链结构.但是,通过应用由二维抛物势、一维光晶格势和二维高斯势所构成的联合外势来构造具有层状的暗孤子结构的方法至今还没有被报道.
本文重点研究由二维抛物势、一维光晶格势和二维高斯势所构成的复合势下的带有增益的三维玻色-爱因斯坦凝聚暗孤子结构.首先,通过能量泛函的方法[18],找到了暗孤子结构的最优化初态.接着,通过大量的数值运算,在参数空间中找到了暗孤子结构的稳定性区域,并分析了处于稳定和不稳定区域之间临界曲线的变化情况;同时,从稳定区域中选取了一个特定的暗孤子结构,对它的稳定性和动力学性质进行了分析,发现在演化过程中,它的振幅和脉宽不断同步增大.最后,对不同原子数比例下的暗孤子结构的中心位置进行了成功的操控.
1 理论模型和能量泛函
带有增益和原子间排斥相互作用的三维玻色-爱因斯坦凝聚的时间演化满足Gross-Pitaevskii(GP)方程[19]
(1)
(2)
与方程(1)对应的能量泛函为
(3)
(4)

(5)
式(5)中,g=4πγ.为了更好地展现物理意义,本文选择具有原子间排斥相互作用的87Rb原子凝聚体作为实验研究数据[21],其中,m=1.44×10-25kg,as/a⊥=4.33×10-3及ω⊥/(2π)=78 Hz,相应的无量纲空间和时间单位为:1.222 μm和2.039×10-3s.
基于外势的圆柱对称结构和每个晶格的扁平形状,笔者提出如下组成暗孤子结构中的基本暗孤子的静态试探波函数:
(6)
式(6)中:z0是基本暗孤子在z轴上的中心位置;k⊥和kz分别是玻色-爱因斯坦凝聚的径向和轴向无量纲脉宽;χ是描述基本暗孤子的拓扑结构因子.由式(6)可知,此基本暗孤子的等振幅图是“轮胎”状的,而χ的大小反映了基本暗孤子的等振幅图“轮胎”的内外半径的大小;φ0代表基本暗孤子的相位;A是归一化常数,
(7)
式(7)中,Γ(ξ)=∫uξ-1exp(-u)du(Reξ>0)是伽马函数.于是,暗孤子结构静态波函数为
(8)
式(8)中:系数m,n,u,p分别是4个基本暗孤子的原子数比例系数.代入无量纲能量泛函式(4)就可得到三维复合势下带有增益的玻色-爱因斯坦凝聚暗孤子结构的能量泛函.接着,通过应用来解决多变量极值问题的粒子群算法[22]求解能量泛函的极值,可得到暗孤子结构静态波函数的最优化解.
2 三维玻色-爱因斯坦凝聚暗孤子结构的动力学分析
首先,把通过应用粒子群算法求解能量泛函的极值得到的暗孤子结构静态波函数最优化解作为直接数值仿真的暗孤子结构初态,并进行大量的数值计算,获得了决定暗孤子结构稳定性的关键参量空间(ω,N,V0)中暗孤子结构的稳定性区域.数值仿真采用Crank-Nicholson算法[23],时间和空间步长分别为0.001和0.045,网格大小为256×256×256,空间范围为-5.76≤x,y,z≤5.76.图1表示在线性增益下原子数比例为1∶1∶1∶1的三维玻色-爱因斯坦凝聚暗孤子结构处于稳定区域和不稳定区域之间的临界曲线的变化情况,临界曲线以上区域是稳定区域,而临界曲线以下区域是不稳定区域.其中,图1(a)是对应于不同的ω时,V0随着原子数N变化的临界曲线.曲线从下往上分别对应:ω=1.3,1.9,2.5,3.1.由图1可知,对于一个特定的ω,V0随着N的增加不断减小.这说明对于一个特定的光晶格宽度,随着原子数的增加,在原子间排斥相互作用、高斯势的排斥作用和线性增益的综合作用下,凝聚体变得更加稳定.而图1(b)是对应于不同的N时,V0随着ω的变化情况.这里,曲线从上往下分别对应:N=1 700,1 300,900,500,100.对于一个特定的原子数N,随着ω的增加,V0先减小后再不断增大.这表明对于一个特定的原子数,随着光晶格的不断变窄,在原子间排斥相互作用、高斯势的排斥作用和线性增益调制下,凝聚体稳定性先增强后不断减弱.考虑到N=500这条曲线在图中的极值点出现在ω=1.5处,为了方便实验实现,选择处于稳定区域中的特定暗孤子结构时,其参量取为:ω=1.5,N=500,V0=50.
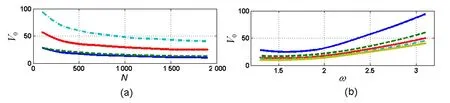
图1 三维玻色-爱因斯坦凝聚暗孤子结构在参量空间(ω,N,V0)上的稳定区域图
然后,从以上稳定区域中选取特定参量及原子数比例的暗孤子结构,并展示了它的稳定演化,如图2所示.图2(a),(b)分别是暗孤子结构的初态和末态在y=0处的切片图.

图2 在线性增益下原子数比例为1∶1∶1∶1的三维玻色-爱因斯坦凝聚暗孤子结构的稳定演化图
从图2(a)可以看出,这是一个层状暗孤子结构,其中4个基本暗孤子分别位于:z=-2π/ω,-π/ω,0,π/ω.将图2(b)与图2(a)比较发现,在演化过程中,各个基本暗孤子的位置未发生改变,但从图中暗孤子结构的形状及颜色深浅的变化可以发现它的密度分布发生了变化.图2(c)是暗孤子的稳定演化图.从图中可以发现,随着演化的进行,等振幅图中4个基本暗孤子所对应的管子直径不断同步变大.这是由于在线性增益的作用下,凝聚体原子数不断增加,使得原子间排斥相互作用不断增大所导致的.为了更清楚地说明这个问题,笔者给出了暗孤子结构中位于z=π/ω处的第4个基本暗孤子的一维振幅演化图,如图2(d)所示,其中曲线从下往上分别对应时刻:t=0,t=15,t=50,t=75,t=100.从图中可以看出,在线性增益的作用下,原子数不断增加,导致了基本暗孤子的振幅和脉宽在演化过程中同步不断变大.同时还发现,在演化过程中,基本暗孤子的中间开口不断变小,而外部直径不断变大.上述暗孤子结构的稳定演化是在由吸引的二维抛物势、一维光晶格势和排斥的二维高斯势所组成的联合外势及线性增益的共同作用下实现的.通过同样的方法,还可得到拓扑结构因子为χ=1,2及由2个或3个基本暗孤子所组成的稳定的暗孤子结构.而拓扑结构因子变化时,暗孤子结构中“轮胎”状基本暗孤子的内外半径也随之发生改变.当拓扑结构因子变小时,基本暗孤子的内外半径同步变小;当拓扑结构因子变大时,内外半径同步变大.
再者,作为对比,在不稳定区域中选择特定参量和原子数比例的暗孤子结构,并展示了它的不稳定演化,如图3所示.由图3可以看出,暗孤子结构中的4个基本暗孤子都发生了不同程度的遂穿现象,而位于两边晶格中的第1个和第4个基本暗孤子由于原子间排斥相互作用所发生的遂穿现象更加严重.宏观量子遂穿现象的出现与参量ω,N和V0有着十分密切的关系.ω,N和V0分别代表光晶格势的空间宽度、凝聚体的原子数及光晶格势的强度.相比于图2中稳定演化的暗孤子结构,这里原子数的增大导致了原子间相互作用强度的增大;并且光晶格势强度V0的变小,也大大增加了凝聚体原子逃逸的概率.总之,在参量ω,N及V0的共同作用下,暗孤子结构发生了显著的量子遂穿现象.
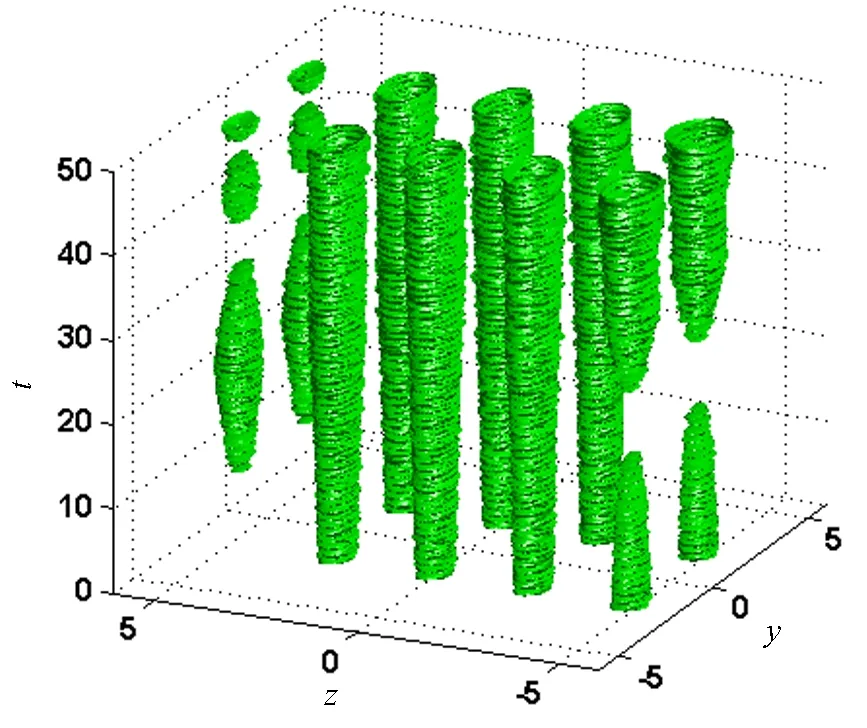
χ=3,A=0.085 7,k⊥=1.303 5,kz=0.586 5,ω=1.3,图3 在线性增益下原子数比例为1∶1∶1∶1的三维玻色-爱因斯坦凝聚暗孤子结构的不稳定演化图
3 三维玻色-爱因斯坦凝聚暗孤子结构中心位置的操控
通过控制外势来操控玻色-爱因斯坦凝聚体[24]是量子调控的中心议题之一.
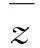
(9)
式(9)中:zi是初位置;zf是末位置;t0是移动的初始时刻;τ是移动所经历的时间.为了控制暗孤子结构在稳定状态下的中心位置定向移动,就得保证移动过程是绝热的,这就要求暗孤子结构的最大移动速度vmax=|zf-zi|/(2π)必须足够小.在线性增益下对带有相同原子数比例和不同原子数比例的三维玻色-爱因斯坦凝聚暗孤子结构的中心位置进行操控的稳定演化如图4所示.图4(a)原子数比例为1∶1∶1∶1,图4(b)则为1∶2∶3∶4.在演化过程中,凝聚体原子数在线性增益的作用下不断增加,致使原子间排斥相互作用不断增大,从而使得等振幅图中的管子直径随着演化的进行不断变大.图4(a)中4个基本暗孤子所对应的管子直径不断同步增大,而图4(b)中管子直径按原子数比例不断增大.在实现线性增益调制的同时,暗孤子结构沿z轴被移动了一个光晶格周期的距离,其中暗孤子结构中第3个基本暗孤子从zi=0移到了zf=π/ω的位置.这里,沿z轴对称的周期性光晶格势的使用能够保证在缓慢地沿着轴移动的过程中保持暗孤子结构的稳定性.
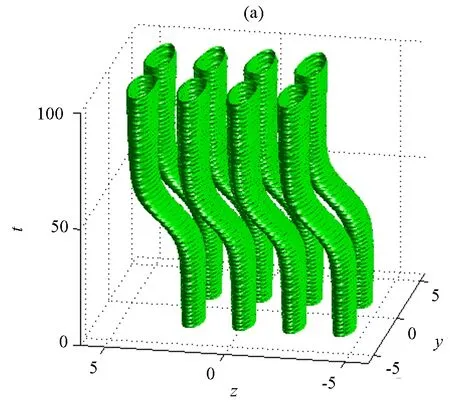
(a)参数同图2;(b)参数为:χ=3,A=0.032 2,k⊥=1.713 6,kz=0.328 5,ω=1.5,
图4 在线性增益下带有相同原子数比例和不同原子数比例的三维玻色-爱因斯坦凝聚暗孤子结构的中心位置操控的稳定演化图

图5 对应于图4(b)的暗孤子结构中4个基本暗孤子的一维振幅演化图
其次,给出了图4(b)中暗孤子结构的4个基本暗孤子的一维振幅演化图.如图5所示,原子数比例从(a)到(d)分别是1∶2∶3∶4.每幅图中曲线从下到上分别对应时刻t=0,20,80,100.从图中可以发现,在线性增益调制的作用下,在暗孤子结构的中心位置被成功地稳定操控过程中,随着原子数的增加,4个基本暗孤子的振幅和脉宽随时间也得到了同步不断变大的操控.需要指出的是,如果玻色-爱因斯坦凝聚系统带有线性损耗,那么随着原子数的减少,暗孤子结构中的4个基本暗孤子的振幅和脉宽随时间将同步不断变小.
笔者已经讨论了三维复合势下的玻色-爱因斯坦凝聚暗孤子结构的存在和稳定性,并通过控制增益和外势实现了对暗孤子结构的振幅、脉宽和中心位置的操控,期待着相关实验不久就能实现.
4 总 结
考虑到由二维抛物势、一维光晶格势和二维高斯势所组成的复合势的圆柱对称结构及每个晶格的扁平形状,笔者构造了一个具有层状结构的在含增益调制及不同原子数比例下的玻色-爱因斯坦凝聚暗孤子结构,并讨论了暗孤子结构的稳定性和操控动力学.首先利用能量泛函的方法,获得了暗孤子结构的最优化初态.接着通过大量的数值仿真,找到了关键参量空间中的稳定性区域,并展示了介于稳定和不稳定区域之间的临界曲线的变化情况.同时,分析了特定暗孤子结构的稳定性和动力学性质.发现在线性增益的作用下,在稳定演化过程中,随着原子数的不断增加,实现了对暗孤子结构中的4个基本暗孤子的振幅和脉宽不断同步变大的控制.再者,通过控制光晶格成功实现了对线性增益下任意原子数比例的暗孤子结构的振幅、脉宽和中心位置的同步操控.这将为量子信息的放大、压缩和存储等提供一定的理论依据.
[1]Liang Z X,Zhang Z D,Liu W M.Dynamics of a bright soliton in Bose-Einstein condensates with time-dependent atomic scattering length in an expulsive parabolic potential[J].Phys Rev Lett,2005,94(5):050402.
[2]Brazhnyi V A,Konotop V V.Evolution of a dark soliton in a parabolic potential:application to Bose-Einstein condensates[J].Phys Rev A,2003,68(4):043613.
[3]Zhang X F,Hu X H,Liu X X,et al.Vector solitons in two-component Bose-Einstein condensates with tunable interactions and harmonic potential[J].Phys Rev A,2009,79(3):033630.
[4]Tempere J,Devreese J T,Abraham E R I.Vortices in Bose-Einstein condensates confined in a multiply connected Laguerre-Gaussian optical trap[J].Phys Rev A,2001,64(2):023603.
[5]Delande D,Sacha K.Many-Body matter-wave dark soliton[J].Phys Rev Lett,2014,112(4):040402.
[6]Dong G,Zhu J,Zhang W P,et al.Polaritonic solitons in a Bose-Einstein condensate trapped in a soft optical lattice[J].Phys Rev Lett,2013,110(25):250401.
[7]Sakaguchi H,Malomed B A.Solitary vortices and gap solitons in rotating optical lattices[J].Phys Rev A,2009,79(4):043606.
[8]Merhasin I M,Malomed B A,Band Y B.Partially incoherent gap solitons in Bose-Einstein condensates[J].Phys Rev A,2006,74(3):033614.
[9]Fujimoto K,Tsubota M.Nonlinear dynamics in a trapped atomic Bose-Einstein condensate induced by an oscillating Gaussian potential[J].Phys Rev A,2011,83(5):053609.
[10]Verkerk P,Lounis B,Salomon C,et al.Dynamics and spatial order of cold cesium atoms in a periodic optical potential[J].Phys Rev Lett,1992,68(26):3861-3864.
[11]Burger S,Bongs K,Dettmer S,et al.Dark Solitons in Bose-Einstein condensates[J].Phys Rev Lett,1999,83(25):5198-5201.
[12]Anderson B P,Haljan P C,Regal C A,et al.Watching dark solitons decay into vortex rings in a Bose-Einstein condensate[J].Phys Rev Lett,2001,86(14):2926-2929.
[13]El G A,Gammal A,Kamchatnov A M.Oblique dark solitons in supersonic flow of a Bose-Einstein condensate[J].Phys Rev Lett,2006,97(18):180405.
[14]Theocharis G,Frantzeskakis D J,Kevrekidis P G,et al.Ring dark solitons and vortex necklaces in Bose-Einstein condensates[J].Phys Rev Lett,2003,90(12):120403.
[15]Hoefer M A,Chang J J,Hamner C,et al.Dark-dark solitons and modulational instability in miscible two-component Bose-Einstein condensates[J].Phys Rev A,2011,84(4):041605.
[16]Achilleos V,Frantzeskakis D J,Kevrekidis P G.Beating dark-dark solitons and Zitterbewegung in spin-orbit-coupled Bose-Einstein condensates[J].Phys Rev A,2014,89(3):033636.
[17]Wang W L,Kevrekidis P G,Carretero-González R,et al.Dark spherical shell solitons in three-dimensional Bose-Einstein condensates:existence,stability,and dynamics[J].Phys Rev A,2016,93(2):023630.
[18]徐志君,施建青,林国成.轴对称谐振势阱中玻色凝聚气体基态和单涡旋态解[J].物理学报,2007,56(2):666-672.
[19]Dalfovo F,Giorgini S,Pitaevskii L P,et al.Theory of Bose-Einstein condensation in trapped gases[J].Rev Mod Phys,1999,71(3):463-512.
[20]Kneer B,Wong T,Vogel K,et al.Generic model of an atom laser[J].Phys Rev A,1998,58(6):4841-4853.
[21]Dalfovo F,Stringari S.Bosons in anisotropic traps:Ground state and vortices[J].Phys Rev A,1996,53(4):2477-2485.
[22]Wang Y C,Lü J,Zhu L,et al.Crystal structure prediction via particle-swarm optimization[J].Phys Rev B,2010,82(9):094116.
[23]Muruganandam P,Adhikari S K.Fortran programs for the time-dependent Gross-Pitaevskii equation in a fully anisotropic trap[J].Comput Phys Commu,2009,180(10):1888-1912.
[24]Theocharis G,Frantzeskakis D J,Carretero-González R,et al.Controlling the motion of dark solitons by means of periodic potentials:application to Bose-Einstein condensates in optical lattices[J].Phys Rev E,2005,71(1):017602.
[25]Kevrekidis P G,Frantzeskakis D J,Carretero-González R.Emergent nonlinear phenomena in Bose-Einstein condensates:theory and Experiment[M].New York:Springer-Verlag,2008:331-352.
(责任编辑 杜利民)
Bose-Einstein condensate dark-soliton structures and manipulation in a three-dimensional complex potential
SHEN Senting, ZONG Fengde, WANG Haihong
(InstituteofNonlinearPhysics,ZhejiangNormalUniversity,Jinhua321004,China)
It was discussed the Bose-Einstein condensate dark-soliton structures with a gain modulation and a layer-chain structure under a complex potential combined of a two-dimensional harmonic potential, a one-dimensional optical lattice and a two-dimensional Gaussian trap. By employing the energy functional method and direct numerical simulations, the stability region of the dark-soliton structures in the parameter space were acquired and their dynamics were analyzed. It was found that the amplitudes and the pulse widths of the dark-soliton structures varied simultaneously under the linear gain modulation. It provided an idea to control the dynamical behaviors of the matter-wave solitons through the gain modulation. Furthermore, the central positions of the dark-soliton structures with different atomic number ratios were manipulated successfully. It would play an important part in the theoretical guidance of the storage and process of the quantum information.
Bose-Einstein condensate; Gross-Pitaevskii equation; dark soliton; manipulation
10.16218/j.issn.1001-5051.2016.04.004
2016-03-19;
2016-04-18
国家自然科学基金资助项目(11072219);浙江省自然科学基金资助项目(Y1080959)
沈森挺(1989-),男,浙江宁波人,硕士研究生.研究方向:玻色-爱因斯坦凝聚. 通信作者:宗丰德.E-mail:fdzong@zjnu.cn
O415
A
1001-5051(2016)04-0379-07

