基于刚柔耦合的水轮机修复机器人导轨误差分析

杜柳青，何 鑫，韩 涛，朱新才

(1.重庆理工大学 机械工程学院，重庆 400054；2.重庆房地产职业学院，重庆 401331)



基于刚柔耦合的水轮机修复机器人导轨误差分析

杜柳青，何 鑫，韩 涛，朱新才

(1.重庆理工大学 机械工程学院，重庆 400054；2.重庆房地产职业学院，重庆 401331)

为了探究导轨式水轮机修复机器人在打磨过程中末端打磨精度问题，提出刚柔耦合仿真方法模拟导轨变形对机器人末端打磨精度的影响。以工业机器人PUMA560为本体建立机器人虚拟模型，并推导机器人正逆运动学解，借助MATLAB和ANSYS完成机器人轨迹规划和导轨柔性化。基于ADAMS仿真环境，模拟刚性体和柔性体导轨条件下的机器人末端打磨轨迹。对比发现导轨变形对机器人末端打磨精度的影响，及启动前期的不稳定状态，为后期导轨式水轮机修复机器人控制研究提供了依据。

刚柔耦合；机器人；导轨；误差分析

0 引言

我国已建或在建的大中型水电站共220座左右，水轮机在长期工作过程中或多或少的存在不同程度的汽蚀和磨损，每隔4到5年就要进行四个多月的停机维修。全国每年由于机组大修减少的发电量达到上万千瓦小时，造成了很大的经济损失[1]。人工堆焊、打磨的传统修复方式需要大量的人力、物力，而且修复精度低、周期长，已经不能满足水轮机修复要求。

国内外对水轮机修复专用机器人做了一定的研究，主要集中在机械臂的结构模态、运动学、动力学、控制策略等的研究[2-5]，但机器人堆焊打磨过程中导轨变形对机械人操作末端精度影响的研究较少。国外对柔性体研究起步较早，多用于航天、机器人、精密机械等行业，柔性体建模方法以浮动坐标系法、绝对节点坐标系法、有限分割法为主[6-7]，国内在刚柔耦合研究方面，孟祥志、刘念聪、朱春霞等人应用于数控机床研究中，得出了机床更精确的动力学特征[8-10]；谢志坤等人应用于激光切割机悬臂梁的动力学仿真研究中，得到了更接近实际的悬臂梁变形和振动情况[11]，表明刚柔耦合仿真方法具有良好的精确性、实用性等特点 。国内外研究在对水轮机修复机器人系统的仿真分析中多把导轨作为刚性体，导致机器人实际修复精度与设计精度存在误差，工程上典型的案例就是我国水电站引进的加拿大魁北克水电局与魁北克大学高等技术学院合作研制的Scompi型机器人在实际作业中达不到预期的效果，调研表明这是由于我国水电站坐落流域水质浑浊，并且含沙量较大，水轮机叶片的磨蚀程度远大于加拿大、美国等Scompi机器人成功应用的国家，磨蚀严重的水轮机需要修复机器人提供更大的磨削力，磨削力引起的导轨变形导致修复机器人产生误差。导轨误差的定量分析迫在眉睫，经过长期研究发现，引入柔性体技术能够很好的解决这一问题。本文提出首先把导轨视为刚性体，运用D-H法推导机器人正逆运动学公式，通过ADAMS与MATLAB联合仿真规划机械人末端打磨轨迹，然后把导轨做柔性处理，采用刚柔耦合联合仿真的方法得到机器人末端打磨位移变化，对比两次轨迹位移证明导轨变形对机器人末端打磨精度的影响，并得出误差曲线。

1 机器人系统构建

1.1 机器人模型的建立

模型的建立是动力学分析的基础，模型数据的准确性和合理性直接关系到仿真结果的正确性。为保证模拟仿真的实用性，采用PUMA560工业机器人的结构和参数建立机械人虚拟样机模型。PUMA560机器人属于多关节旋转式机器人，由6个杆件和6个转动关节构成，末端执行器与杆件6相连，基座与大地固结，6个关节拥有6个自由度，所以PUMA560机器人是6自由度的操作臂。和大多数工业机器人一样，PUMA560机器人按照Pieper准则设计，后三个关节轴线交于一点，其连杆坐标系统[12](图1)，其中a2=431.8mm，a3=20.32mm，d2=149.09mm，d4=433.07mm。

图1 PUMA560机器人机器人连杆坐标系统

1.2 机器人正逆运动学分析

机器人正运动是指在所有关节变量已知时，计算机器人各杆件上任意点的位姿[13]。采用D-H法建立PUMA560机器人基座与手爪之间的正运动变换矩阵如下式：

0T6=0T1·1T2·2T3·3T4·4T5·5T6=

(1)

式(1)是PUMA560机器人总变换矩阵0T6，前三列表示机器人的位置变化，后三列表示机器人的姿态变化，描述了机器人末端执行器坐标系与基座坐标的位姿变换，是进行运动分析的基础，后面的逆运动学分析也是基于此求解得出。

机器人逆运动是指根据机器人末端执行器的位姿，求解各关节角度变量，是正运动学的逆过程[11]。通过控制各关节上的驱动电机，使机器人末端执行器达到相应的位置。逆运动的求解在机器人的运动学、动力学、控制方式中起到不可或缺的作用，逆运动学算法的性能直接影响控制算法的性能，并与控制的快速性和准确性有直接的联系。逆运动解是复杂的，尤其是多关节机器人，各关节运动学解的耦合严重，往往具有多解性[14]。PUMA560机器人的前三个关节控制末端执行器的位置，后三个关节控制末端执行器的姿态，导轨的变形主要影响机械人末端执行器位置的变化，所以在仿真过程中，只驱动机器人前三个位置关节，保持后三个姿态关节不动。

采用代数法求逆运动反解[15]，用逆变换Z(〗WTHX〗0T-11左乘0T6得：

(2)式(2)中末端位姿矢量已经给定，即n,o,a,p为已知，根据矩阵对应相等原理，可列出12个等式方程，求解出：

(3)

(4)

(5)式(3)～式(5)中：A=c1px+s1py，s2=sinθ2，c2=cosθ2，以此类推。逆运动学解是进行轨迹规划的理论前提。

1.3 机器人末端轨迹规划

机器人轨迹规划是根据运动学分析研究机器人各关节角度等变化规律[16-17]。为方便对比导轨分别视为刚性体和柔性体时机器人末端轨迹，让机器人在X-Z平面内沿Z轴方向上行走一段直线轨迹，即从点A(431.8,171.08,0)到点B(431.8,171.08,300)(单位mm)。运用上面的逆运动学解，采用插值法，在MATLAB Robotic toolbox中求出θ1、θ2、θ3的逆运动解的，并整理为时间-关节角度的数据表格，即导入ADMAS中的spline曲线数据。θ1、θ2、θ3随时间变化的曲线如图2，图2中可以看出关节1和关节2的转角变化较小，关节3的转角变化较大，这是由于机器人末端是在X-Z平面内沿Z轴方向上直线运动，此段路径上关节3为主要运动关节，关节1和关节2只是辅助运动，用来保证机器人末端运动的直线性，3个关节的转角变化曲线与预想情况一样，并且三条曲线变化平稳，没有出现突变，表明了路径规划的合理性。

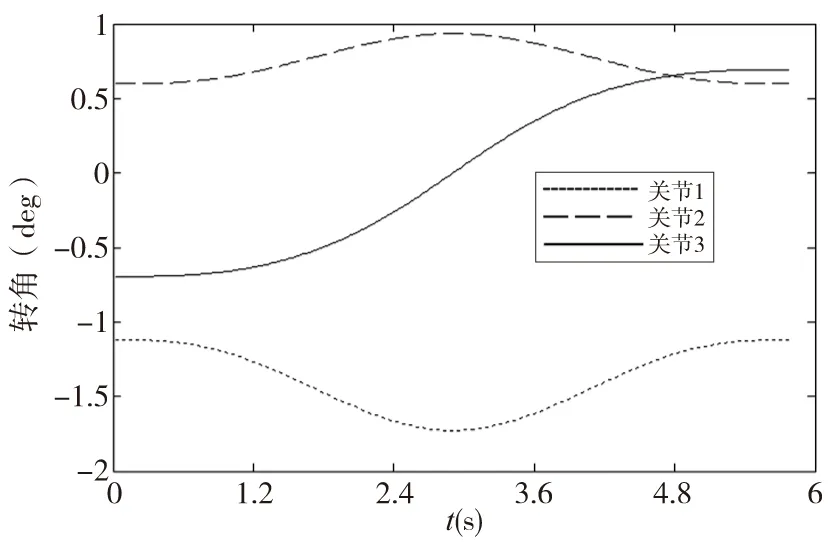
图2 关节转角变化曲线

2 刚性体仿真

机器人在执行堆焊打磨等工作时，通过电磁装置与导轨固定相连，导轨是最终的受力部件，其变形量的大小会直接影响机械臂末端打磨精度，同时6个关节也会放大末端误差。把机器人和导轨作为整体进行仿真，采用ADAMS直接建模的方法，减少了三维建模导入ADAMS时数据传输的误差，并在导轨两端加入两个固定块以模拟导轨两端固定的受力场景，其整体模型如图3所示。

图3 系统整体模型

建立模型后，对模型施加约束和驱动，包括4个固定副、6个旋转副、6个驱动电机，其中前三个关节使用AKISPL函数加载MATLAB中规划的Spline曲线，后三个关节保持不变。为模拟机器人在打磨时的工况，在机器人末端施加切削力40N、压紧力80N、打磨工具重力300N[18]，设置仿真时长为6s、步长为500进行仿真，得到机器人末端测量点在X、Y、Z轴上的位移变化如图4 ，并保存仿真结果为rigid_sim，由图4可知机器人末端在X、Y轴方向上位移不变，Z轴方向上位移由0mm～300mm直线变化，与设计的路径完全一致，同时各方向上位移变化均匀，表明水轮机修复机器人系统模型设计合理，能够有效的完成预设路径。

图4 末端测量点位移变化曲线

3 刚柔耦合联合仿真

机器人在打磨过程中，基座与导轨固定相连，导轨是最终的受力部件，并且其变形对整体精度影响较大，所以把导轨作为柔性体，与视为刚性体的机器人建立刚柔耦合模型。由于ADAMS自身的柔性化处理精度不够，将导轨以Parasolid格式导入ANSYS，单元类型选择Solid187和MASS21，定义弹性模量E=200GPa，泊松比ε=0.3，密度ρ=7850kg/m3，并在三个接触面建立刚性区域，生成柔性体导轨如图5，图5中的灰色圆部分是刚性区域，最后输出MNF格式的模态中性文件。

图5 导轨柔性体模型

以MNF模态中性文件替换整体模型中的刚性体导轨，导轨上的约束副会自动转换到柔性体上，在原仿真条件下进行刚柔耦合仿真，保存仿真结果为flex_sim，机器人末端测量点上X、Y、Z轴方向的位移变化对比如图6～图8，图6～图8 中实线是刚性体导轨仿真得到的机器人末端位移曲线，虚线是柔性体导轨仿真得到的机器人末端位移变化曲线，可以看出实线与虚线之间存在一定的距离，说明柔性体导轨的受力变形引起了机器人末端的位移变化，刚性体导轨在仿真过程中是存在误差的。机器人末端测量点在X，Y方向的位移误差曲线如图9、图10，图9是用图6所示虚线减去实线后得到的机器人末端在X轴方向位移误差曲线，图10是用图7所示实线减去虚线后得到的机器人末端在Y轴方向位移误差曲线，位移误差曲线定量的显示了在施加一定的力和力矩情况下，采用刚性体导轨进行仿真后机器人末端X、Y轴方向产生的位移误差。

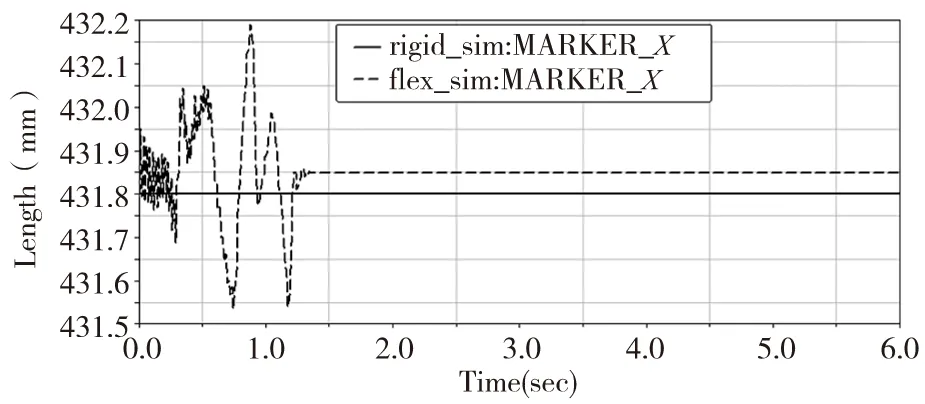
图6 末端测量点X轴方向位移变化曲线

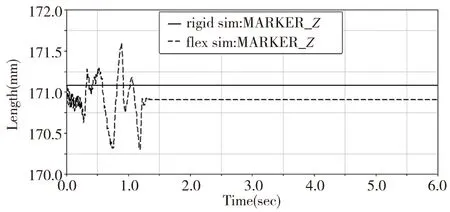
图7 末端测量点Y轴方向位移变化曲线

图8 末端测量点Z轴方向位移变化曲线

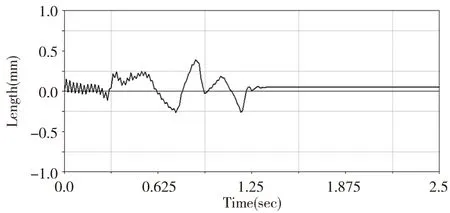
图9 末端X轴方向位移误差曲线

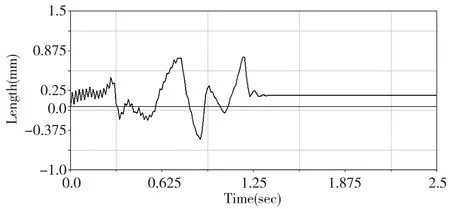
图10 末端Y轴方向位移误差曲线

对比图6～图8可知导轨的变形对机器人末端的影响主要集中在X、Y轴方向，Z轴方向的影响几乎可以忽略不计，这是因为导轨的变形主要由基座对导轨的力矩引起的。由图6、图7可知0～1.3s时末端位移曲线出现波动，说明整个系统需要1.3s左右的时间到达稳定工作状态，所以在实际打磨工作中，中途停止打磨后重新启动应设置系统进入稳定状态的时间，以免影响打磨精度。柔性体导轨仿真系统进入稳定作业状态后，机器人末端X、Y方向的位移比刚性体导轨仿真系统的传统分析位移分别偏移了0.1mm、0.4mm，这些偏移产生的误差在传统分析过程中是被忽略了的，但是这些误差在水轮机修复机器人实际作业过程中也会产生，应优化控制系统，通过前三个关节的反馈控制进行补偿。

4 结论

(1)本文在建立水轮机修复机器人系统模型时选取了工业机器人PUMA560的数据参数，保证了仿真分析的实用性和可靠性。采用D-H法推导PUMA560机器人正逆运动学公式，并借助MATLAB Robotic toolbox规划机器人作业路径，避免了在MATLAB中直接用插值法进行路径规划带来的巨大计算量，并为机器人系统在ADAMS中的仿真提供了数据，同时水轮机修复机器人系统在ADAMS虚拟环境下的仿真结果证明了机器人系统模型的正确性和路径规划的合理性。

(2)在传统分析中，机器人系统中的导轨都是以刚性体处理，导致水轮机修复机器人在实际作业过程中会产生误差。本文提出把导轨作为柔性体，进行刚柔耦合仿真得到分析结果，并与刚性体导轨分析结果进行对比，发现导轨变形引起了机器人末端位置误差，其误差主要集中在机器人力矩导致的轴向和法向误差，在常规的打磨条件下，机器人末端产生的法向和轴向误差分别在0.1mm和0.4mm左右，为进一步的控制研究提供了数据支持。

[1] 陈金金, 李丽荣,陈阳,等. 水轮机叶片修复专用机器人的发展现状及应用展望[J]. 机械, 2011, 38(7): 1-6.

[2] 马凯威, 刘建春, 黄海滨,等. 机器人磨抛机机身结构的模糊优化设计[J]. 组合机床与自动化加工技术, 2015(8): 47-50.

[3] 袁安富, 沈思思, 余莉,等. 基于ADAMS 和MATLAB 的喷涂机器人运动仿真研究[J]. 组合机床与自动化加工技术, 2014 (8): 44-48.

[4] 褚金钱, 徐方. 基于Solidworks 与Matlab 的码垛机器人动力学仿真[J]. 组合机床与自动化加工技术, 2013 (9): 28-31.

[5] 董伯麟, 鞠毅. 基于量子框架的六自由度机器人控制系统研究[J]. 组合机床与自动化加工技术, 2015(12): 85-89.

[6] Mirue, Choi. Flexible dynamics and attitude control of a square solar sail[D]. Ann Arbor:ProQuest LLC, 2015.

[7] AHMED A. SHABANA. Flexible multibody dynamics: review of past and recent developments[J]. Multibody System Dynamics, 1997(1): 189-222.

[8] 孟祥志, 赵柏庆. 基于ADAMS 的3-TPS 混联机床动态特性分析[J]. 机床与液压, 2014, 42(9): 6-9.

[9] 刘念聪, 谢进, 杨勇,等. 基于刚柔耦合的数控进给工作台动态特性分析[J]. 组合机床与自动化加工技术, 2015(12): 12-14.

[10] 朱春霞, 朱立达, 刘永贤,等. 基于ADAMS的并联机床刚柔耦合系统的协同建模研究[J]. 组合机床与自动化加工技术, 2007(11): 1-5.

[11] 谢志坤, 史科科, 刘伯聪,等. 某激光切割机悬臂梁的动力学仿真研究[J]. 组合机床与自动化加工技术, 2013 (7): 19-21.

[12] 殷际英, 何广平. 关节型机器人[M]. 北京:化学工业出版社, 2003.

[13] 王晓强, 王帅军, 刘建亭. 基于MATLAB的IRB2400工业机器人运动学分析[J]. 机床与液压, 2014, 42(3): 54-57.

[14] 康博. 工业机器人轨迹跟踪控制算法研究[D]. 广州:华南理工大学, 2012.

[15] Saeed B Niku. Introduction to robotics:analysis, system, applications[M]. Englewood Cliff:Prentice Hall, 2001.

[16] 王鲁平, 朱华炳, 秦磊. 基于MATLAB 的工业机器人码垛单元轨迹规划[J]. 组合机床与自动化加工技术, 2014(11): 129-132.

[17] 张云峰, 马振书, 孙华刚,等. 一种基于混合策略的排爆机器人目标抓取轨迹规划[J]. 机床与液压, 2015, 43(21): 86-90.

[18] 金晓强, 季林鸿, 王子儀,等. 水轮机叶片坑内修复机器人修磨方式研究[J]. 机械设计与制造, 2008(1): 186-189.

(编辑 李秀敏)

Error Analysis for Rail of Turbine Repair Robot Based on Rigid-flexible Coupling

DU Liu-qing1, HE Xin1, HAN Tao1,ZHU Xin-cai2

(1.College of Mechanical Engineering,Chongqing University of Technology ,Chongqing 400054,China;2.Chongqing Real Estate College,Chongqing 401331,China)

In order to explore grinding accuracy problem of turbine repair robot in the process of grinding,rail deformation effect robot end grinding precision based on the method of rigid-flexible coupling.It builds robot virtual model based on the data of industrial PUMA560 robot,completes robot trajectory planning and flexible rail in MATLAB and ANSYS,it simulate robot end grinding trajectory when rail regard respectively as a rigid body and flexible body.Rail deformation effect robot end grinding trajectory through compared,and robot has instability state in the early time,it provides the gists for turbine repair robot control research.

rigid-flexible coupling;robot;rail;error analysis

1001-2265(2016)11-0084-04

10.13462/j.cnki.mmtamt.2016.11.023

2016-01-18；

2016-02-24

国家自然科学基金青年基金(51305476)

杜柳青(1975—)，女，重庆长寿县人，重庆理工大学教授，硕士，研究方向为数控机床精度设计，(E-mail)Lqdu1@126.com。

TH122；TG659

A