基于SOM神经网络聚类以及支持向量机的数控机床热误差建模方法的研究

陈 卓，李自汉，杨建国，姚晓栋

(上海交通大学 机械与动力工程学院，上海 200240)



基于SOM神经网络聚类以及支持向量机的数控机床热误差建模方法的研究

陈 卓，李自汉，杨建国，姚晓栋

(上海交通大学 机械与动力工程学院，上海 200240)

为了减小主轴季节性热误差影响，提高机床的加工精度，提出了基于针对机床热源进行SOM神经网络预聚类后的支持向量回归机的主轴热误差综合模型。针对一台型号为HTM40100h的车铣复合中心，对主轴的关键温度测点进行了内外热源的划分，并在冬夏两个季节对所有测温点温度和热误差数据进行采集，将外部热源温度数据作为SOM网络的输入变量进行季节性聚类，聚类后的外部热源温度数据连同同时刻的内部热源温度数据一起作为不同季节支持向量回归机模型的输入变量，得到热误差拟合值。将通过聚类预处理的方法与未经聚类的方法进行了对比试验，结果表明：该综合预测模型在冬夏两个季节均获得了较高的建模精度和鲁棒性。

机床热误差建模；SOM神经网络；支持向量回归机；季节性预聚类

0 引言

数控机床在加工工件的过程中，会产生加工误差。按照原因的不同，这些误差包括热误差、几何误差、切削力误差等[1]。其中由机床热变形引起的误差占到了总误差的40%以上。因此，机床热误差的实时补偿技术的研究对于工程实践而言显得极为迫切而重要。而在热误差补偿技术中，机床热误差建模又是所有问题中最重要的一环，不仅仅是因为它高度概括地将生产实践中的实际问题抽象为了数学模型，使得工程技术人员可以采用信息化手段着手解决，也因为要得到一个具有好的鲁棒性和稳定性的热误差模型是极为困难且难以实现的。

在机床各个部件中，机床主轴是因为热变形导致产生加工误差的最主要部件之一[2]。从上世纪八十年代开始，国内外许多学者对此进行了深入探讨和研究，总结出了很多极具价值的建模算法，包括最小二乘法建模[3]、BP神经网络模型[4]、灰色系统神经网络模型[5]，多项式拟合与纵向建模[6]，因子分析与贝叶斯估计建模方法[7]等。

近些年的研究更多的认为，导致机床产生热误差的原因分为两类，即内部热源和外部热源。其中内部热源包括机床在加工过程中的切削热、进给轴的滚珠丝杠螺母发热以及驱动电机发热等等；外部热源则主要归结为环境温度的变化。这样分类的目的是希望能较好地区别不同季节、不同环境温度下机床所产生的热误差，从而区别对待，建立更具鲁棒性的模型。而国内外很多学者的研究也充分说明了这样做的有效性，比如上海交通大学的李自汉等人提出了对于滚珠丝杠温度的时间模型[8]，通过建立机床热量传递的模型，将滚珠丝杠温度和室温的差值与滚珠丝杠温度上升曲线的斜率联系起来，从而建立了机床运行(热机)时与(停机)冷机时的滚珠丝杠温度的时间模型，因为考虑了环境温度作为外部热源，模型具有较高精度；又比如华中科技大学的Bo Tan等人，将传统机床热误差模型鲁棒性不强的原因归结为机床对于环境温度的热迟滞效应[9]，并且将机床误差明确分为由内部热源引起的误差以及由外部热源引起的误差，对于外部热源引起的误差，通过采用时序法建立全年环境温度模型，从而建立了基于傅里叶级数分解的热误差模型，而对于内部热源引起的误差，则采用传统的多元线性回归法进行建模，合成模型具有很高的鲁棒性并且较好地解决了不同环境温度下的热误差模型鲁棒性不足的问题。

在建模方法的讨论上，近年来机器学习领域中发展起来的支持向量机(support vector machine)理论具备了很多传统神经网络模型所不具备的优势，包括[10]：

(1)具有较好地处理非线性问题的能力。

(2)具备全局最优解，避免了神经网络的局部极值问题。

(3)较高的计算效率，因为经过训练后的支持向量只占训练样本的很小一部分，因此极大地节省了存储空间。

(4)相较于神经网络模型，可以更好地处理高维输入向量。

因此，支持向量机是一种有效的机器学习方法，在建立机床热误差数学模型的应用中具有独特的优势。

同时，为获得具有较高鲁棒性的误差模型，Ramesh, R等人提出了对误差进行分类的思想[11-12]。其中，文献[10]介绍了一种采用支持向量机对不同载荷下的热误差进行分类后，再次采用支持向量回归机(support vector regression machine, SVRM)进行建模的方法，具有一定参考价值。而文献[13]在算法层面上提出了基于SOM神经网络聚类的SVM模型，具有一定新颖性。

受此启发，结合上文提到的机床内外热源的概念，本文提出了一种基于SOM神经网络聚类的支持向量回归机热误差模型(SOM-SVRM)，旨在通过利用自组织特征映射神经网络(Self-Organizing Feature Map Neural Networks, SOM NN)良好的聚类性能，将样本数据中不同季节由外部热源所左右的机床温度数据进行分类后，分别采用支持向量回归机对所有机床测温点(包括内部热源测温点和外部热源测温点)所得温度数据进行热误差建模的方法来提高模型的鲁棒性和通用性。该方法特点如下：

(1)利用SOM神经网络可以对不同季节的机床外部热源温度数据进行有效的分类。通过对SOM神经网络的训练，不断调整其输出层的权值系数，最终使网络具有针对不同模式的温度输入向量的聚类能力，有效区分数控机床在不同季节的外部热源温度数据，将其结合同时刻的内部热源温度数据传递给下游支持向量回归机进行建模。

(2)采用支持向量机对经神经网络聚类后的内外热源温度数据集进行热误差的建模。

模型结构图如图1所示。

图1 SOM-SVRM模型结构图

本文首先介绍了针对机床热误差的SOM神经网络聚类和支持向量回归机建模原理，其后针对同一台机床在冬夏两个季节的相同工况下所采集的温度数据进行热误差建模，并将结果与单一季节模型建模结果进行比较，用以验证。

1 温度测点的优化和内外热源的区分

在模型建立之前，需要确定哪些温度测点对于机床来说是内部热源，哪些是外部热源。这里提出一种根据所测温度数据在一天内与环境温度之差的大小进行确定的方法。

针对所测量的机床，在选取了适量温度测点后，截取其在一天24h内所测数据进行分析，计算该测温点与当天室内环境温度的差值的绝对值ΔT并绘制曲线，分析该曲线的波动情况。

为简便起见，这里仅分析ΔT的最大值。根据实测温度数据分析可得如下结论：如果ΔT最大值ΔTmax<5℃则可认为该测温点主要受外部环境热源影响，即该点数据对于机床热误差为外部热源温度数据，该点的数据将作为SOM神经网络分类器的输入的一部分。反之，则为内部热源温度数据，该点温度将在SVRM回归机模型中作为输入数据的一部分。

假设外部热源由n个传感器的数据组成，内部热源由m个传感器的数据组成，则SOM网络的输入向量为n维，SVRM模型的输入向量为n+m维。

2 SOM神经网络原理

自组织特征映射神经网络的运行包括网络的训练和工作阶段[10]，训练阶段包括竞争、合作和更新三个过程，竞争过程确定获胜神经元，合作过程确定获胜邻域，更新过程改变邻域内神经元的权值。SOM神经网络的拓扑结构分为两层，包括输入层和输出层，其中输入层神经元仅仅起到简单传递输入样本的作用，而输出层神经元分布在二维、三维甚至更高维的网格中。 设样本数据为u=(u1,u2,…,uN)T∈RN，即分布在机床上的N个温度传感器所测温度值，则输入层包含N个神经元。设输出层(即为竞争层)，包含M个神经元，其中每个神经元都与输入层神经元以一定权值连接，权值为ωij(i=1,2,…,N；j=1,2,…,M)。任意一个竞争层神经元的权值向量为ωj=(ω1j,ω2j,ω3j,…,ωNj)T∈RN。故竞争层神经元的输入：

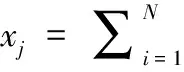
(1)

竞争层神经元的输出为yj=f(xj)。 f(x)在搭建完神经网络的结构之后，就可以开始对其进行学习训练。自组织特征映射学习网络的学习算法依次包括以下步骤[10]：

初始化→采样→竞争→合作→自适应(即权值调整)→更新学习率→判断循环是否结束。

限于篇幅，这里不对每一流程详细展开，读者可查阅相关资料或者参考文献。

经过以上的学习过程，SOM神经网络应当具备了对输入向量的聚类功能。而聚类的过程如下：

(1)对经过学习后的SOM网络输出层各神经元标以记号，以表示该神经元所对应的季节类型；

(2)将待检样本(即由外部热源温度数据组成的输入向量)输入到SOM神经网络中；

(3)若竞争层(即输出层)获胜神经元在输出层的位置与某季节神经元的位置相同，说明该输入温度数据属于该种季节的数据。若获胜神经元在竞争层的位置介于不同季节神经元之间，说明该输入温度数据为两季节之交所采集得到的数据，且其更靠近哪一个季节由该位置与某季节标准样本的位置的欧氏距离决定。

温度数据经过SOM聚类之后，便可以分别输入到不同的支持向量机模型中进行热误差建模(见图2)。

图2 二维自组织特征映射神经网络结构图

3 支持向量回归机(SVRM)模型原理

机床热误差模型是典型的非线性模型，热误差与温度或者开机时间、转速等因素的函数关系不呈线性。因此，对于该问题的建模应当采用支持向量机的非线性回归模型。限于篇幅，关于SVRM的相关数学推导和演算，本文不作深入探讨。这里直接给出如下回归函数：

f(x)=w·φ(x)+b

(2)

该回归函数是通过将分类问题中的广义最优超平面的法向量w最小化问题(即二次凸优化问题)转化为求解拉格朗日函数的对偶变量的最大值问题而导出的[14]，其中x为经过SOM神经网络聚类之后的训练样本点。在求解二次凸优化问题时还需要确定的参数包括ε损失系数以及惩罚系数C。经过计算之后得到回归函数为下式[14]：

(3)

(4)

k(xi,x)=exp-|x-xi|22σ2

(5)

其中,σ是函数的宽度参数，控制着函数的径向作用范围。

这样，在求解过程中需要确定的参数有：惩罚系数C，损失系数以及核函数中的宽度参数σ，可以通过经验确定，也可以通过粒子群算法等算法进行优化得到[16]。

4 实验与仿真

依据本文的观点，对一台型号为HTM40100h的车铣复合中心进行了误差补偿实验。限于篇幅，这里仅就该方法在冬季和夏季的机床主轴x向热漂移误差建模效果进行评估。根据有关机床温度布点优化实验和理论分析结论[17]，对机床床身的测温点进行了优化布置，最终确认一共使用4个测温点，其分布以及所属热源类别如表1所示。同时，在刀架上安装基恩士激光位移传感器，用于测量主轴的热误差。

表1 所属热源类别

4.1 实验方案

实验方案如下：

(1)在冬季和夏季两个季节中分别选取比较有代表性的一天进行机床温度和热误差测量，该组温度数据和热误差数据用于建模，标以实验1组和实验2组。

(2)在所选取的测量日之后第二天使机床冷机，第三天进行同样的测量，并且要求同季节两次测量时环境温度最高值和最低值相差不大于5℃。该组数据用于验证模型。标以验证1组和验证2组。

(3)在四个测量日，以早晨六点作为测量初始点，使机床开机，主轴以恒定转速空切削，持续运行5h(300min)，获得在此时间段内的温度和热误差数据。

这样，一共获得四组温度和热误差数据。实验1组和2组用于模型的建立，验证1组和2组用于验证模型的精度。根据方案，所选择的测量日分别为：

夏季：2013年7月20日数据作为实验1组，2013年7月22日数据作为验证1组。

冬季：2014年12月8日数据作为实验1组，2014年12月10日数据作为验证2组。

4.2 SOM网络的训练和分类应用

首先须建立SOM网络模型，这里运用matlab神经网络工具箱建立一个竞争层包括36个神经元的SOM网络[18]，其拓扑结构如图3所示。将实验1组和实验2组数据中的外部热源温度向量(二维向量)代入SOM

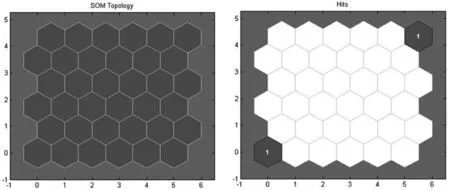
图3 SOM神经网络拓扑结构 图4 SOM网络神经元分类结果

网络进行训练，训练次数上限设定为100次。训练后的网络中各个神经元的分类如图4所示。图中左下角和右上角的两个神经元分别代表冬季和夏季两个季节，神经元标号分别为1和36。

如果输入数据在神经网络的竞争层中激发两个神经元中的某一个，或者其邻近区域内某一神经元，则代表该输入温度数据属于相应季节的数据。这里从验证组选取四组温度数据进行分类测试，包含两组夏季温度数据和两组冬季温度数据，如表2所示。定义变量result代表测试结果，其值即为输入数据在SOM网络竞争层激起的获胜神经元的标号。

表2 SOM分类测试温度数据表

分类测试结果如表3所示。

表3 SOM数据分类测试结果

可见，经过100次训练的网络可以很精确地区分夏季和冬季温度数据。

4.3 支持向量回归机模型的训练和误差预测应用

在完成了对外部热源温度向量的分类之后，即可将对SVR模型进行训练和建模。这里分别给出夏季和冬季两次验证组预测误差的结果，如图5所示。其中误差数据采集自数控机床主轴在300min内的径向热漂移。由图可见，无论是冬季还是夏季模型，预测的残差被成功控制在±0.5μm以内，模型的精确性和鲁棒性得到了很好的验证。而之所以夏季热误差拟合结果更可观的原因可能是夏季热误差在开始的上升阶段的上升趋势趋于平稳，这样会更加利于模型的学习，而出现这样的现象的原因主要是数控机床主轴在夏季室温以及机床温度本身较高，开机到机床达到热平衡的热机阶段温升较小，且趋势缓慢，因此热变形趋势趋于平缓，而冬季室温较低，热机阶段机床温度迅速攀升，导致主轴热误差增长趋势也较陡峭。如果未经分类，将夏季温度数据代入冬季模型进行预测并且将冬季温度数据代入夏季模型进行预测可得到如图6所示结果。可见，如果不对温度数据采取分类处理，拟合残差明显增大，模型将失去其鲁棒性。

(a)冬季误差拟合结果

(b)夏季误差拟合结果

图5 主轴热漂移误差补偿结果

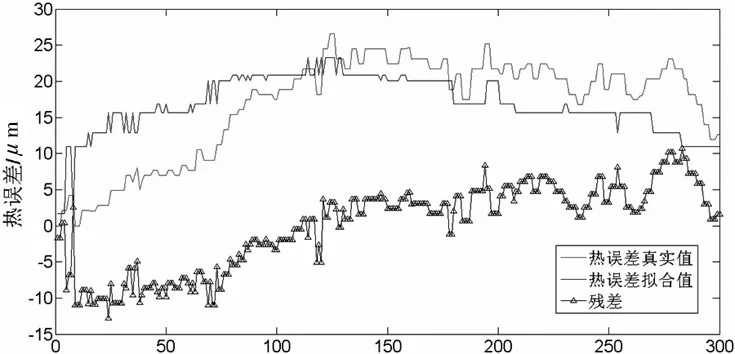
(a)夏季模型拟合冬季热误差结果

(b)冬季模型拟合夏季热误差结果

图6 冬夏两季模型与数据交叉拟合结果

5 结束语

本文提出利用SOM-SVR模型对于不同季节的机床热误差进行了建模和预测，研究结果表明采用SOM对数据进行预分类之后的支持向量机模型具有较高的精度，采用该模型对不同季节机床热误差进行拟合前后的残差值被控制在5μm以内，因此该模型适用于不同季节复杂工况下的机床热误差建模和预测，并被运用于数控机床热误差补偿领域。本文在完善了机床热误差建模方法的同时，提出了根据不同季节机床所表现出的不同温升趋势来进行热误差建模的思想，在热误差建模季节性预分类领域踏出了第一步。

另外，在数控机床误差预分类建模领域仍有亟需改进之处，具体包括：

(1)对于机床内外热源的划分方法较为简单，如果可能，可以采用其他分类方法加以区分，如机理分析法以及有限元分析法。

(2)由于当内部热源与环境温度温差增大时，内部热源对于机床热误差的影响会随之增大，可考虑在模型公式中加入权重因子，针对不同的内外热源温差调整输入向量中各项的值，从而更加精确地模拟不同季节的情况。

(3)如何将分类建模的方法扩展到全年任何季度仍须深入研究，这意味着某一季度的SVR模型将能够适应环境温度的连续渐变。这需要在全年不同时段采集多组机床热误差数据，分析其渐变趋势和机理，并建立更有针对性的模型。

[1] 杨建国．数控机床误差综合补偿技术及应用[D]．上海:上海交通大学,1998.

[2] Chang Long Zhao, Yi Qiang Wang, Xue Song Guan. The thermal error prediction of NC machine tool based on LS-SVM and Grey Theory [J]. Applied Mechanics and Materials, 2009,16-19: 410-414.

[3] 杨建国，任永强，朱卫斌，等．数控机床热误差补偿模型在线修正方法研究[J]．机械工程学报，2003，39(3):81-84.

[4] 杨漪, 姚晓栋,杨建国,等．基于主成分分析与BP神经网络相结合的机床主轴热漂移误差建[J]. 上海交通大学学报，2013，47(5):750-753.

[5] 张毅.数控机床误差测量、建模及网络群控实时补偿系统研究[D]. 上海:上海交通大学,2013.

[6] 朱小龙, 杨建国,代贵松.数控机床定位误差全温度综合建模及实时补偿[J]. 组合机床与自动化加工技术, 2014(5):83-86.

[7] 代贵松,杨建国,朱小龙.基于因子分析和贝叶斯估计的机床热误差建模[J]. 组合机床与自动化加工技术, 2013(9):5-8.

[8] Zihan Li, Kaiguo Fan.Time-varying positioning error modeling and compensation for ball screw systems based on simulation and experimental analysis[J]. International Journal of Advanced Manufacturing Technology, 2014,73(5-8):773-782.

[9] Bo Tan.A thermal error model for large machine tools that considers environmental thermal hysteresis effects. International Journal of Advanced Manufacturing Technology, 2014,82-83: 11-20.

[10] 韩敏.人工神经网络基础[M]. 大连: 大连理工大学出版社,2014.

[11] R Ramesh, M A Mannan.Support Vector Machines Model for Classification of Thermal Error in Machine Tools[J]. International Journal of Advanced Manufacturing Technology, 2002, 20(2),114-120.

[12] R Ramesh, M A Mannan.Al-based classification methodologies for the modelling of machine tool thermal error[J]. Technical Paper-Society of Manufacturing Engineers. MR, 2002, MR02-192,1-8.

[13] 王文剑.支持向量机建模及应用[M]. 北京:科学出版社, 2014.

[14] 苗恩铭,龚亚运,成天驹,等.支持向量回归机在数控加工中心热误差建模中的应用[J]. 光学精密工程, 2013, 21(4):980-986.

[15] Lin, Weiqing.Support Vector Machine and Neural Network united system for NC machine tool thermal error modeling[C].Proceedings-2010 6th International Conference on Natural Computation, 2010,8,4305-4309.

[16] 熊伟丽.粒子群算法在支持向量机参数选择优化中的应用研究[A]. 中国控制与决策学术年会论文集[C].沈阳, 东北大学出版社, 2007:447-449.

[17] Li Y X.Optimization of measuring points for machine tool thermal error based on grey system theory[J]. International Journal of Advanced Manufacturing Technology, 2008, 35(7-8): 745-750.

[18] 史峰.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社, 2010.

(编辑 李秀敏)

Modeling for Thermal Error of Machine Tool Based on SOM Neural Network and Support Vector Regression Machine

CHEN Zhuo，LI Zi-han，YANG Jian-guo，YAO Xiao-dong

(School of Mechanical Engineering,Shanghai Jiao Tong University，Shanghai 200240，China)

In order to reduce the impact of seasonal thermal error of spindle on CNC machine tool, a novel method of modeling based on preclassification by SOM neural network and Support Vector Regression Machine(SVRM) is proposed. Experiment was performed on a HTM40100h turning milling machining center. Temperature and error data both in Summer and Winter were collected, and the measuring points of temperature on machine tool were classified into internal heat sources points and external ones. The temperature data of external heat sources points were input into SOM neural network for seasonal classification. The data of classified external heat sources points along with the meanwhile data from internal heat sources points were input into corresponding SVRM model for error fitting. The comparison between modelling with and without preclassification shows that, the former one presents much better robustness and precision in two different seasons.

machine tool; SOM neural network; support vector regression machine; seasonal preclassification

1001-2265(2016)11-0068-05

10.13462/j.cnki.mmtamt.2016.11.019

2015-12-07；

2016-01-06

上海市军民结合产业发展体系建设项目(JMJH2013002)；上海市闵行区产学研项目(2013MH111)；辽宁省科技创新重大专项(201301001)；上海市产学研项目(沪CXY-2013-29)

陈卓(1989—)，男，长沙人，上海交通大学硕士研究生，研究方向为机床主轴热误差测量和补偿，(E-mail)john02142005@sjtu.edu.cn；杨建国(1951—)，男，上海人，上海交通大学教授，博士生导师，研究方向为精密加工与测试，数控机床误差检测、建模、补偿，(E-mail)jgyang@sjtu.edu.cn。

TH132；TG659

A