TX1600G镗铣加工中心工作台进给系统耦合温度场的分析与研究

李兴山，吴德莉，祝振林

(沈阳理工大学 机械工程学院，沈阳 110159)



TX1600G镗铣加工中心工作台进给系统耦合温度场的分析与研究

李兴山，吴德莉，祝振林

(沈阳理工大学 机械工程学院，沈阳 110159)

针对进给系统存在的热载荷引起的热变形问题，建立TX1600G镗铣加工中心工作台进给系统的热结构耦合模型,在系统稳态温度场分析的基础上对其进行了热结构耦合分析。分析进给系统的温度场和热变形，得出轴承发热对系统热变形影响最大，而系统热变形对机床Y轴精度影响较大的结论；提出采用中空丝杠来减小热变形,使丝杠轴的变形减少了约42%，系统其他零部件的变形减少了约30%。

镗铣加工中心；进给系统；热-结构耦合

0 引言

机床进给系统处于机床加工传动链的最后一环，其热变形将直接影响机床的加工精度。研究分析表明，热误差占机床总误差的40%～70%[1]。因此研究进给系统热特性，找出其温度分布及热变形规律，对于热误差补偿，提高机床加工精度具有重要的意义[2]。

国内外研究者已经对进给系统热特性进行了相关的研究：Kmisk等通过有限元法建立机床滚珠丝杠进给系统的温度场[3]。郑州大学的郭松路等对加工中心进给系统的热特性进行研究[4]。

本文以TX1600G工作台进给系统为研究对象，用有限元软件ANSYS Workbench对其进行热-结构耦合分析，综合考虑热和结构载荷的影响得到更符合工况与可靠性要求的分析结果。

1 工作台进给系统结构

TX1600G采用龙门式铣削结构与卧式镗削结构相结合的结构布局，主要由床身、立柱、工作台、滑台、滑枕以及主轴箱等组成。

镗铣加工中心工作台进给系统主要由床身、工作台、导轨副、滚珠丝杠副等零部件组成。进给系统采用伺服电机通过联轴器直接驱动，由滚珠丝杠副带动工作台沿Z轴运动，行程为1750mm，工作台也可旋转。为有限元分析考虑，适当简化床身，将丝杠简化成等直径的阶梯光轴，轴承简化成等直径的空心圆柱体，忽略倒角、圆角、小孔等不重要的特征[5]，简化后剖开的模型见图1。

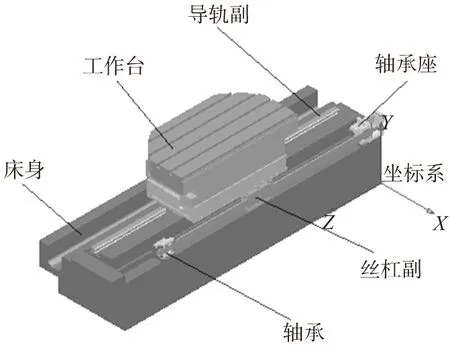
图1 工作台进给系统简化模型

2 热载荷和热边界条件的计算

对于稳态热分析，流入系统的热量加上系统自身产生的热量等于流出系统的热量，模型任意一点温度恒定。所以，进行稳态热分析时要计算出热源产生的热量和对流换热系数，计算方法如下。

2.1 热源分析

机床工作过程中，工作台进给系统热源主要包括伺服电机损耗发热、丝杠与轴承及螺母之间的摩擦发热、导轨副的摩擦发热。本机床采用的联轴器具有隔热作用，因此忽略电机损耗发热的影响[6]。

(1)轴承的发热

滚动轴承的发热主要由滚动体与套圈之间的摩擦力矩及润滑剂流体损耗引起的，发热量公式[7]：

Q=2πnM/60

(1)

式中，n为转速；M=M0+M1，其中M0为润滑剂粘性引起的摩擦力矩，M1为外加载荷力矩。

进给系统的前、后轴承都采用角接触球轴承，转速为1500r/min，根据上述公式求得轴承的生热率为141158W/m3。

(2)滚珠丝杠副发热

滚珠丝杠副的发热原理和滚动轴承的发热原理基本相同。因此，滚珠丝杠副摩擦发热量也可用公式(1)计算。摩擦力矩M由丝杠的驱动力矩MD和预紧力的阻力矩MP组成，其中：

MD=FDP2πη(1-η2)

(2)

MP=FPP2πη(1-η2)

(3)

式中，P为丝杠的导程；η为丝杠螺母的传动效率；FD为丝杠螺母所受轴向力；FP为预紧力。

滚珠丝杠副摩擦发热的43%经接触面传导至丝杠轴[8]，可得丝杠轴上与螺母接触处热流密度为1620W/m2，螺母内表面热流密度为2150W/m2。

(3)导轨副的发热

滚动支撑直线进给系统中，导轨和滑块发热量按如下公式计算[9]：

Q=μFv

(4)

式中，μ为滚动摩擦系数；F为施加于摩擦面的载荷；v为工作台运动速度。

这里假设导轨副摩擦产生热量的一半传导至导轨，可以求出导轨副的热流密度为510W/m2。

2.2 对流换热系数的分析

本文分析的内容中，由于温度较低，辐射量较小，可以忽略，只考虑热对流。

(1)自然对流换热

进给系统外表面与空气发生自然对流换热，将进给系统外表面对流边界设置为简单空气对流，即Stagnant Air-Simplified Case。

(2)丝杠轴与空气的强迫对流换热

机床工作过程中，丝杠以一定速度旋转，会加快与空气的对流，属于强迫对流换热，对流换热系数计算公式为：

h=λNuL

(5)

Nu=0.133Re23Pr13

(6)

(7)

式中，λ为导热系数；L为特征尺寸；Nu为努谢尔特数；Re为雷诺数；Pr为普朗特数；ω为丝杠角速度；d为丝杠直径；ν为空气的运动粘度。

环境温度为22℃时，空气的导热系数为0.026W/(m·℃)，空气的普朗特数为0.7，空气的运动粘度为15.5m2/s，计算出丝杠与空气的强迫对流换热系数为65W/(m2·℃)。

(3)轴承与润滑脂的强迫对流换热

轴承采用脂润滑，对流换热系数公式如下：

(8)

润滑脂的导热系数为0.9W/(m·℃)，普朗特数为400，求得对流换热系数为235W/(m2·℃)。

(4)滚珠丝杠副与润滑油的强迫对流换热

滚珠丝杠副采用油润滑，对流换热公式如下：

(9)

润滑油的导热系数为0.3W/(m·℃)，普朗特数为360，求得对流换热系数为430W/(m2·℃)。

3 温度场分析

3.1 有限元模型的建立

将简化模型导入ANSYS Workbench中，定义材料属性，设置接触，采用自由网格划分法划分网格，然后对丝杠、螺母、轴承、导轨、滑块等小的零部件进行细化，建立有限元模型，如图2所示。

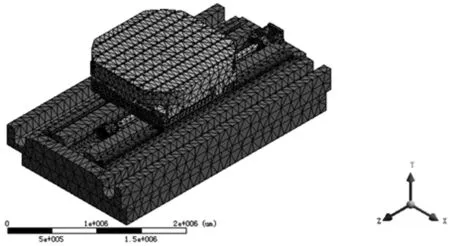
图2 进给系统有限元模型

3.2 稳态温度场分析

设置分析类型为稳态热分析，环境温度22℃，将计算出的热载荷加载到有限元模型上，得到其稳态温度场，由于温度场左右对称，则将模型沿Z轴剖开如图3所示。

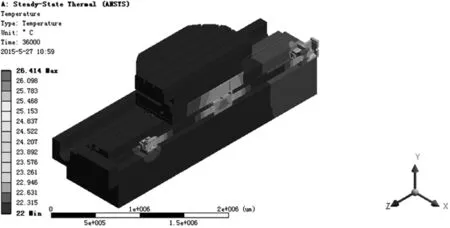
图3 进给系统稳态温度场云图

由图3看出进给系统温度场的分布情况，对于床身、导轨副以及工作台来说，温度变化不是很明显，而丝杠螺母副、轴承及轴承座温升较大。系统最高温度为26.4℃，出现在前轴承组处。螺母及后轴承处次之，其平均温度分别为25.7℃和24.8℃。

4 热-结构耦合分析

在ANSYS Workbench中，主要的载荷和约束分为惯性载荷、结构载荷、结构支撑和热载荷。本文首先将稳态分析温度场作为热载荷加载到模型上；其次对进给系统整体施加重力加速度，对丝杠施加预紧力,工作台表面施加工件的重量，镗削力作为远程载荷施加到工作台上；最后对床身与地面施加全约束。约束和载荷加载后，对模型进行求解，得到进给系统热变形云图如图4所示。最大变形量为12.561μm，出现在前轴承座处。此外，丝杠螺母副及两端轴承处也有较明显的热变形，而导轨、滑块、工作台和床身等零部件由于温升较小，其变形也较小。

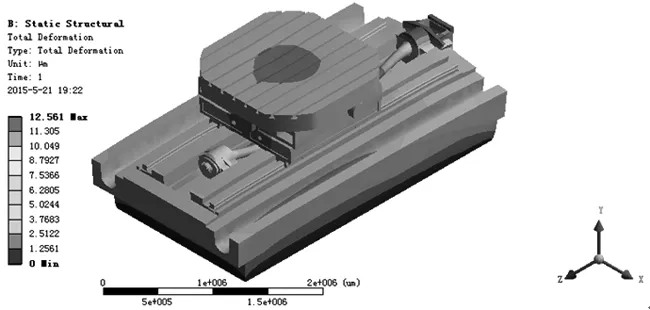
图4 进给系统总变形云图

观察进给系统三个方向的热变形云图，见图5～图7，发现工作台上表面Y轴位移约为4.5μm，Z轴位移约为1.8μm，X轴位移约为1μm，说明进给系统热变形对Y轴精度影响较大。

图5 进给系统X向热变形云图

图6 进给系统Y向变形云图

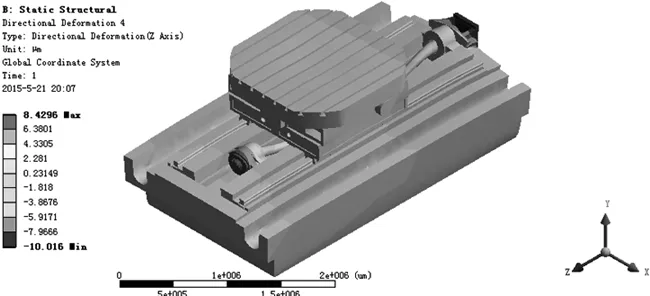
图7 进给系统Z向变形云图

5 改进措施及效果

滚珠丝杠副是进给系统中非常关键的部件，它的精度决定着机床传动的精度，因此优化滚珠丝杠副，减少其热变形非常重要。本文采用中空冷却丝杠，降低温升，减小热变形。

5.1 丝杠与冷却液的对流换热

对于中空丝杠，可以通水或通油冷却，但是由于水的粘度小，比热和密度大，所以冷却效果比油好[10]，因此采用通水冷却。丝杠与冷却水之间对流换热系数按如下公式计算：

h=λfdNμf

(10)

(11)

(12)

式中，λ热传导系数，d为中空丝杠内孔直径，Nμf为努谢尔特数，v为丝杠中心孔流体平均速度，d0为丝杠轴直径，νf为流体的运动粘度。

丝杠轴公称直径为80mm，中空孔直径取20mm，冷却水流量取2L/min，求得换热系数为2619W/(m2·℃)。

5.2 改进前后分析结果对比

将热载荷和结构载荷加载到改进后的有限元模型上，得到其热变形云图，如图8所示。

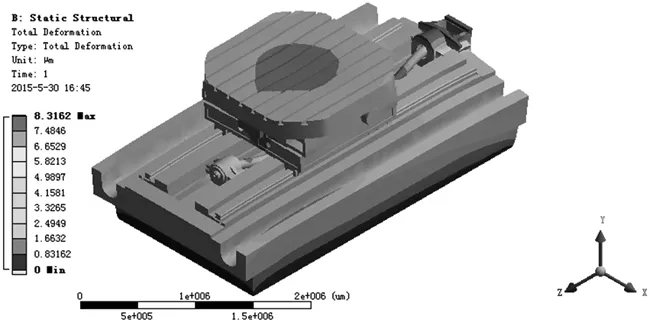
图8 改进后进给系统总变形云图

对比改进前后进给系统各零部件的热变形云图，最大变形量的具体对比数据见表1。

表1 改进前后分析结果对比 μm

由表1可知，改进后进给系统各零部件特别是丝杠轴的热变形明显减小，说明采用中空冷却丝杠对丝杠轴以及其它部件热变形起到了一定的抑制作用，从而提高工作台进给系统的精度。

6 结论

机床工作过程中，进给系统主要由轴承和丝杠螺母的发热导致温升，进而引起热变形。分析结果表明前轴承组发热对热变形影响最大，进给系统热变形对机床Y轴精度影响较大。本文采用中空冷却丝杠来改善丝杠的冷却条件，降低温升，抑制丝杠轴的热变形，提高进给系统的定位精度。同时，由于冷却条件的改善，其它零部件的温升及热变形也减小，从而提高机床的加工精度。

[1] R Ramesh,M A Mannan,A N Poo.Error compensation in machine tools-a review Part II:thermal errors[J].International Journal of Machine tool & manufacture,2000(40):1257-1284.

[2] J Bryan.International Status of Thermal Error Research[J]. Annals of the CIRP,1990,39(2):645-656.

[3] S K Kim,D W Cho.Real-time estimation of temperature distribution in a ball-screw system[J]. International Journal of Machine Tools&Manufacture,1997,37(4):451-464.

[4] 郭松路，盛艳君，刘德平.基于ANSYS的加工中心进给系统热特性分析[J].组合机床与自动化加工技术，2013(12):21-24.

[5] 王春霞.机械传动件的热变形理论及应用研究[D].合肥:安徽大学，2009.

[6] 周芝庭，冯建芬.基于ANSYS的加工中心机床热特性有限元分析[J].机械制造与自动化，2008(6)：22-24.

[7] 杨海栗,田建平,胡勇,等.龙门加工中心丝杠组件热态性能与温度场实验研究[J].组合机床与自动化加工技术，2015(6):4-8.

[8] 钟名东.高速高精度数控车床滚珠丝杠进给系统热态特性研究[D].南昌:华东交通大学，2011.

[9] 纪艳丽.数控机床直线进给系统热特性分析技术研究和工具开发[D].南京:南京理工大学，2014.

[10] 芮执元，张传辉，郭俊峰.基于有限元法的中空冷却滚珠丝杠温升及热变形研究[J].机械设计，2011(12)：17-20.

(编辑 赵蓉)

Analysis of the Coupling Temperature Field for the Table Feeding System of TX1600G Boring-Milling Machining Center

LI Xing-shan, WU De-li, ZHU Zhen-lin

(School of Mechanical Engineering, Shenyang Ligong University, Shenyang 110159,China)

In view of thermal deformation caused by heat load in the feeding system, the thermal-structure coupling model for the table feeding system of TX1600G boring-milling machining center is established, and thermal-structure coupling analysis is conducted based on temperature field analysis. The steady temperature field and thermal deformation of the feeding system indicate that the heat output of bearings has the largest effect on the deformation of the system and the thermal deformation affects the Y-axis precision machine tool greatly. And using hollow screw to reduce thermal deformation has been put forward, so that the deformation of the screw is reduced by about 42%, the deformation of other parts is decreased by about 30%.

boring-milling machining center; feeding system; thermal-structure coupling

1001-2265(2016)11-0028-03

10.13462/j.cnki.mmtamt.2016.11.008

2015-06-02；

2015-06-25

国家863项目(2012AA041303)；辽宁省自然科学基金资助项目(201602645)

李兴山(1971—)，男，辽宁鞍山人，沈阳理工大学教授，博士，研究方向为并联机床、虚拟样机、CAD/CAM应用技术，(E-mail)lxs7241@sina.com。

TH133.2；TG659

A