1种叶片气膜冷却效果试验评估的新方法

曹智顺，王洪斌，张树林，张联合，徐晓利

（中国航发沈阳航空发动机研究所，沈阳110015）

1种叶片气膜冷却效果试验评估的新方法

曹智顺，王洪斌，张树林，张联合，徐晓利

（中国航发沈阳航空发动机研究所，沈阳110015）

由于试验误差的存在，导致试验评估气冷叶片冷却效果的试验结论具有一定的不确定性。直接应用M onte-Carlo法会出现统计不合理物理过程的情况，使得评估结果过于安全，为了更准确的描述试验结果，提出了1种基于区域映射M onte-Carlo法的分析方法。改进的区域映射M onte-Carlo法考虑了分散性因素的内在联系，有效降低了结果的分散性。并以某涡轮叶片为例，应用区域映射M onte-Carlo法分析，得到了该叶片冷却效果的概率分布特性。结果表明：该方法实用性较强，可应用于气膜冷却叶片的冷却效果试验评估。

气膜冷却；叶片；概率分布；试验评估；区域映射；M onte-Carlo；航空发动机

0 引言

随着对燃气涡轮发动机可靠性和高效性的追求，涡轮前燃气温度越来越高，给涡轮叶片冷却技术的设计提出了更高要求[1-2]。气膜冷却是航空发动机涡轮叶片广泛采用的有效冷却技术之一[3-5]，准确评估气膜冷却效果对涡轮叶片的设计至关重要。试验是评估气膜冷却效果的重要手段之一，国外早在20世纪60年代就对气冷叶片进行了试验研究[6]，中国多位学者也从不同角度进行了叶片的冷效试验[7-9]。试验方法在冷却效果的评估方面优势明显，可以真实地反映试验件的冷却效果。但当试验用压缩空气出现不稳定波动时，将导致主要试验参数产生随机性，极易造成采集数据的不同步，使得同时刻的参数数据不能直接应用。因此，以确定性的试验结果评估叶片的冷却效果可信度较差。由于在发动机其他领域设计中也存在类似问题，因此，国内外众多学者将概率论引入发动机设计评估领域[10-12]。对于冷却效果的试验评估可参考类似方法，即以具有概率特性的评估结果替代单一的确定性试验结果，以数据轴为主要分析依据，消除数据时间不同步的影响。与概率论相结合，常采用Monte-Carlo抽样法，在确定影响因素的概率分布特性基础上，大量抽样得到目标值的概率分布特性。而在冷却效果的评估试验中，直接应用Monte-Carlo法，没有考虑数据间的内在联系，结果包含了不符合实际物理过程的情况，导致评估结果过于安全。

本文提出1种分析叶片冷却效果分布特性的区域映射Monte-Carlo分析方法。该方法在Monte-Carlo方法基础上，结合稳态换热的实际物理过程，统计样本间的有效区域数据，在保证安全性的前提下，有效降低了评估结果的分散性。同时该方法具有应用简单、保持试验状态时间短、后期分析节约成本等特点。本文以某涡轮叶片为例，采用该方法得到其冷却效果的概率分布特性，在冷却效果的试验评估方面具有较强的实用性。

1 区域映射Monte-Carlo分析法

使用区域映射Monte-Carlo法分析叶片冷却效果的具体分析过程，如图1所示。

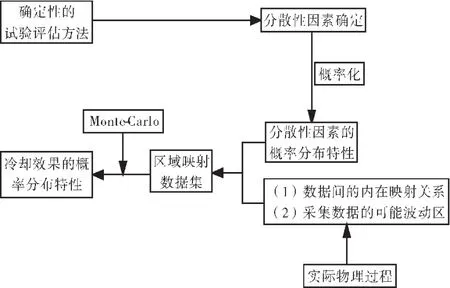
图1 区域映射Monte-Carlo法分析过程

使用该方法进行冷却效果分析，前提是将试验状态调整到设计点状态，并保持一定的时间，采集足够多的采样数据。一般采用数据历史均值为主要指标，即随着采样数据的增加，按采样数据重新计算的数据平均值。假设某组数据n的历史均值为m，当继续抽样n组数据时，其历史均值不再明显变化，则认为该组数据n可以反映该数值的分布规律。否则，数据数量不足以表达统计规律。

如图1所示，该方法在采集足够的试验数据后，主要包含以下4个关键步骤。（1）确定影响试验结果的各因素，并充分考虑其分散性，将分散性因素概率化，使其带有概率特性；（2）结合稳态换热的实际物理过程，考虑数据间的内在联系，对原始采集数据进行修正，建立合理的分散性因素采集数据集；（3）在分散性因素采集数据集内，考虑分散性因素的概率特性，建立区域映射数据集；（4）以区域映射数据集为基础数据，使用Monte-Carlo分析方法，得到具有概率特性的冷却效果。下面就该方法的几个关键技术环节详细阐述。

1.1 分散性因素的确定

叶片冷却效果，又称综合冷效或有效温比，其定义源于壁面稳态换热微分方程

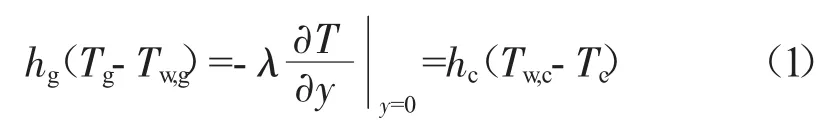
式中：hg为燃气与叶片壁面换热系数；hc为冷气与叶片壁面换热系数；λ为导热系数。

当假定壁面内外温度均匀时（由于叶片壁面很薄，该温差相对很小），冷效定义为[13]

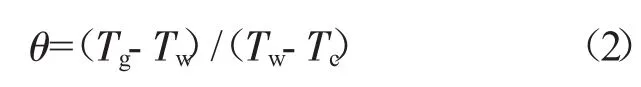
式中：Tw,g为燃气侧叶片表面壁温；Tw,c为冷气侧叶片表面壁温；Tg为燃气温度；Tc为冷气温度；Tw为叶片壁面温度。

在工程中通常将式（2）中分母的温差改写成燃气与冷气的温差，即

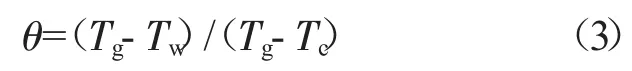
当平均壁温与燃气温度相等时，冷却效果为0；当平均壁温与冷气温度相等时，冷却效果为1。

研究表明，冷却效果主要受到燃气与冷气温比、冷气与燃气流量比、燃气马赫数和雷诺数的影响。当试验状态点十分接近设计点状态时，燃气和冷气的流量和压力变化很小，故流量比、马赫数和雷诺数的变化是微弱的，可以忽略不计。但微弱的扰动却可能带来3个温度值的较大变化，由式（2）可知，对于冷却效果的试验评估结果将造成不可预知的影响。因此，分析冷却效果的概率分布特性，主要考虑3个温度值分散性的影响。

1.2 分散性因素的概率分布特性分析方法

影响冷却效果评估的3个温度值的分散性主要受到气源的波动和温度值的测量两方面的影响。

1.2.1 气源波动分散性分析的样本数据采集

试验中压缩气源的微弱波动，将造成燃气、冷气温度的独立变化以及由此联动产生的壁温变化。因此，讨论气源波动对温度的影响，实际是讨论燃气与冷气的温比对冷却效果的影响。

在试验状态保持不变的条件下，对燃气、冷气温度和壁温进行n次采样。概率论的大数定律认为，当抽样次数n足够大时，某一数值的出现频率与其出现的概率相一致。本文的方法就是以此为依据，采用数据出现的频率来统计数据的概率。

1.2.2 测量分散性分析的样本空间

在试验中，测温电偶的测量受到材料、工艺等因素随机变动的影响，而这些因素的波动在正常情况下是相互独立的，且均不起决定性作用，故认为是可以叠加的。在概率论的极限理论中可以证明：具有上述特点的随机变数一般都可以认为是服从正态分布的[14]。服从正态分布的数据满足3σ准则（σ为标准差），即当期望值为u时，数值分布在（u-3σ，u+3σ）之中的概率为0.9974。

因此，对于元件本身的随机性误差分析，可以认为其服从正态分布，数学期望为测量实际值，标准差满足3σ=测量误差限。以此为基准，离散一定数量的样本空间，使样本空间的均值历史趋于平稳的样本数量，可以认为能够反映测量分散性的分布规律。

1.3 Monte-Carlo分析方法

通过对不确定性因素的分析，可以得到3个温度的概率分布特性，但其分布规律不一定符合某种特定的分布形式。对此可以采用Monte-Carlo的方法分析冷却效果的概率分布特性[15]。

Monte-Carlo方法又称随机抽样技巧或统计试验方法，其理论基础是概率论中的大数定律和贝努力原理，其原理如下：设功能函数Z=g（X1,X2,…,Xi,…,Xn），式中Xi为具有任意分布的随机变量。对X进行N次随机抽样，带入到功能函数中，得到N组Zj=（j=1,2…,N）的值。设在N个Zj值中存在Nf个Zj＜0，则Zj＜0概率可以表示为

设冷却效果θ=g（Tg,Tc,Tw），式中3个温度是具有任意分布的随机变量。对3个温度进行N次随机抽样，带入到功能函数中，得到N组θi值，设在N个θi值中存在Nf个θi＜θd，则冷却效果θ＜θd的概率可以表示为

直接使用Monte-Carlo法，输入具有任意分布的3个温度，按式（3）进行足够的抽样次数，可以得到冷却效果的概率分布特性，并以式（5）按一定概率给出评估结果。

1.4 区域映射Monte-Carlo法

直接使用Monte-Carlo法充分考虑了影响因素的分散性，但没有考虑数据间的内在联系。

试验件的冷却效果在某个状态点的值是一定的，但由于燃气和冷气的温度变化，必然会导致壁温的变化。直接应用的Monte-Carlo法，显然忽略了这种映射关系，实际包含了数据内低燃气温度值匹配高壁温水平以及高燃气温度值匹配低壁温水平的不合理物理过程，使冷却效果的结论过于安全。因此，准确的评估冷却效果，必须要考虑数据之间的内在联系。

不考虑测量误差的影响，保持某一状态参数不变，气源的波动导致燃气和冷气在某个值附近出现的频率较多，也必然导致壁温在某个值附近出现的频率较多。大数定律认为3个温度最大概率密度处的值更能反映三者的内在物理联系。但是在试验过程中，由于气源的微弱扰动，使得燃气温度不可避免地产生瞬时跳动。若壁温由于电偶的迟滞性未能同步变动，直接应用采集数据将导致评估结果不真实。为规避燃气瞬时跳动而引起的采样数据虚值，在冷却效果评估时，需考虑有可能瞬时跳动到概率密度最大值处的所有数据。

分析全部采样数据，计算相邻采样数据的差值（下一时刻数据与上一时刻数据差值）如图2所示。该差值绝对值的大小反映了数据瞬时跳动的步长，正负号反映了采样数据瞬时跳动的方向。设差值的最大值为区域上边界（正值），最小值为区域下边界（负值）。取单位长度（温度的单位长度为1℃）为基本数据区域，以最大概率密度处基本数据区域为基准，考虑区域上、下边界，计算可得到映射数据区域范围。

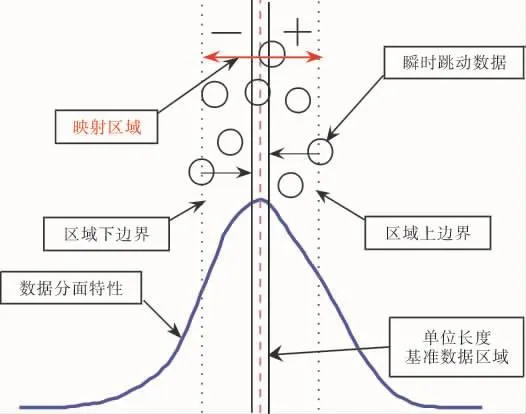
图2 区域数据统计分析方法

在映射区域数据内，使用第1.2.2节中方法，考虑采样数据的测量误差，可以得到考虑映射关系的3个温度数据集，以此按第1.3节所述方法进行Monte-Carlo抽样，按式（4）可得到较直接Monte-Carlo法更精确的冷却效果概率分布特性。

该方法具体分析流程如图3所示。包含4个主要分析部分，优先进行气源波动、测量误差和区域映射分析，最后使用Monte-Carlo分析得到冷却效果的概率分布特性。

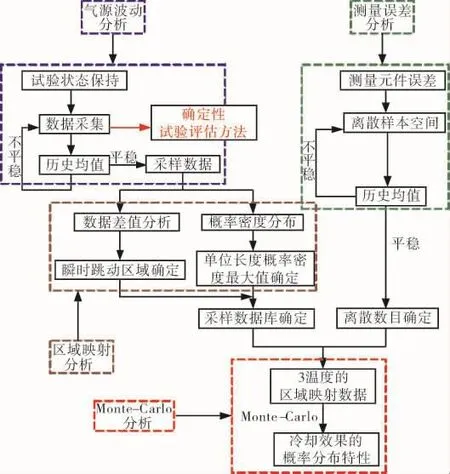
图3 区域映射Monte-Carlo法分析流程

2 某叶片冷却效果的概率分布特性分析

依据上述分析方法，以某叶片为例分析其冷却效果的概率分布特性。

2.1 气源波动分析

为采集足够的试验数据，叶片在设计点状态保持153 s，记录各温度试验数据153个，各温度均值历史如图4～6所示。从图中可见，在140个数据附近趋于平稳，可见153个数据足够统计气源波动引起的温度分散性的分布规律。使用1.2.1节所述方法，分析3个温度的概率密度分布形式如图7～9所示。

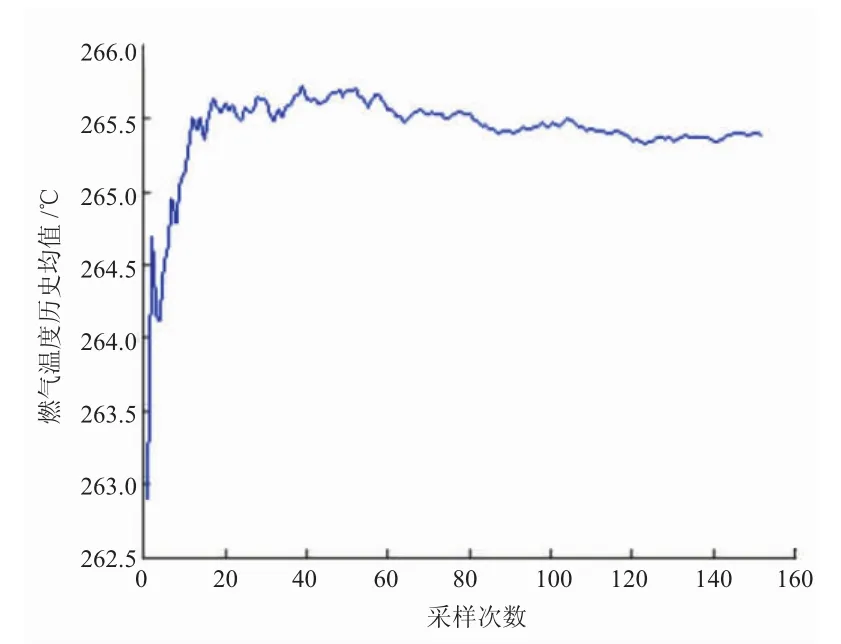
图4 燃气温度历史均值

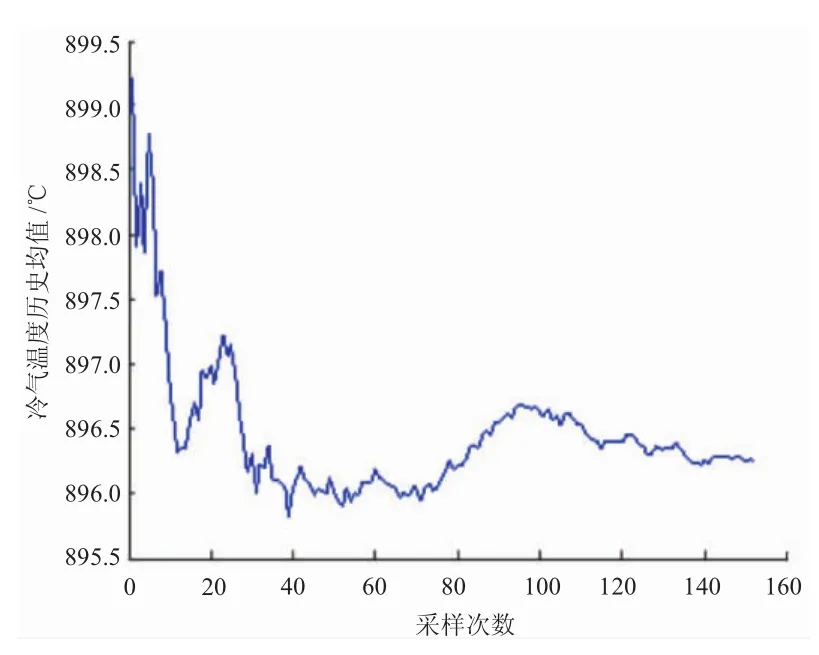
图5 冷气温度历史均值

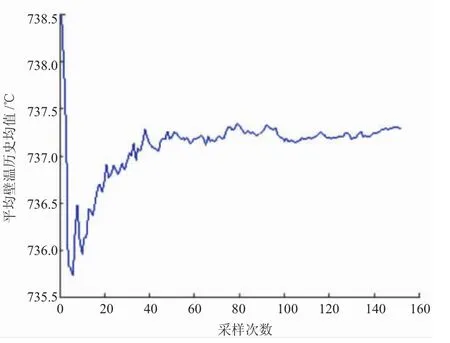
图6 平均壁温历史均值

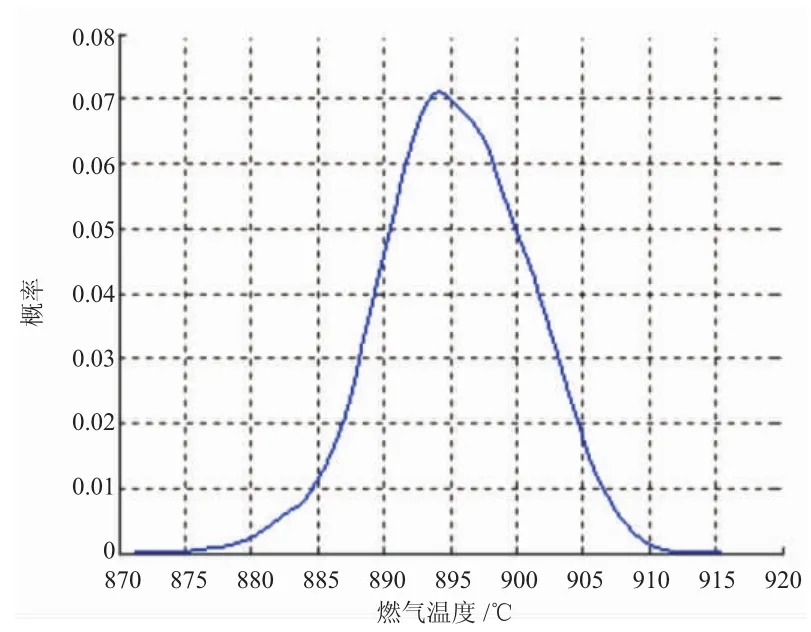
图7 燃气温度概率分布

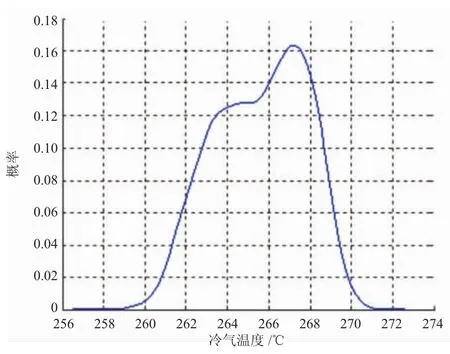
图8 冷气温度概率分布

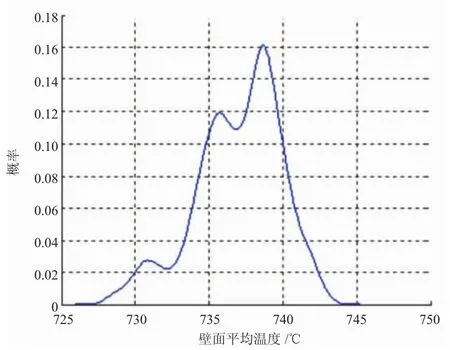
图9 壁面平均温度的概率分布

2.2 测量误差分析

查得燃气和冷气的测温电偶的测量精度为1%t（t为实测温度值），叶片表面壁温电偶测量精度为0.75%t。依据第1.2.2节的分析方法，建立所有实测数据测量值分散性的正态分布公式。以此为基础，随机抽样100个抽样数据，以某一燃气温度抽样数据均值历史为例，在80个左右各温度均值历史趋于平稳，如图10所示。可见100个子样足够统计测温电偶引起的温度测量分散性的分布规律。

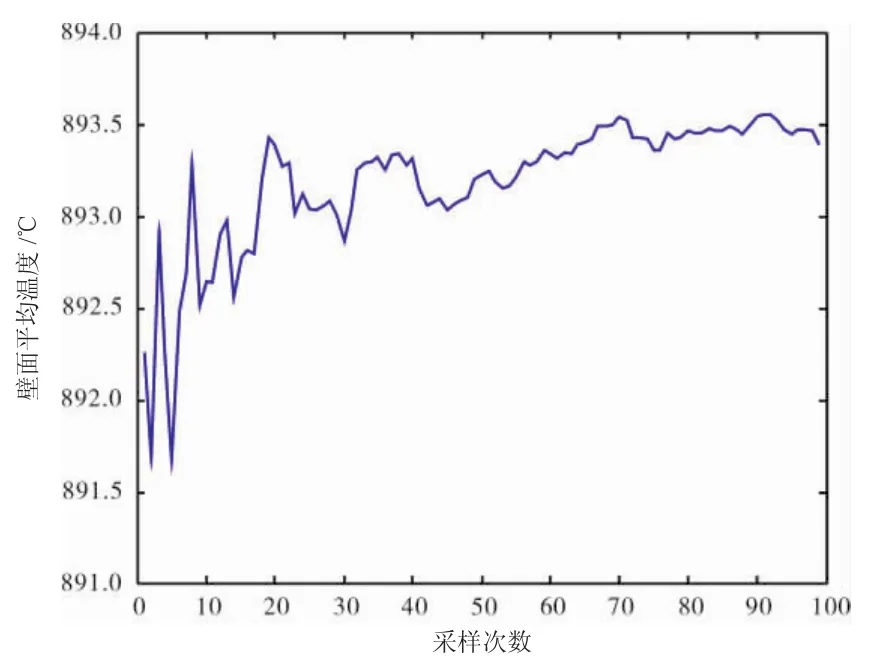
图10 壁面平均温度的概率分布

2.3 区域映射分析

按第1.4节的方法，分析全部采样数据（图7～9），以最大概率密度处基本数据区域为基准，可分析3个温度的单位长度基本数据区域。计算相邻采样数据的差值，分析采样数值跳动如图11～13所示，取差值的最大值为区域上边界（正值），最小值为区域下边界（负值）。由此可计算区域映射数据区域范围，见表1。表1中区域上、下边界反映了数据瞬时跳动的程度。以燃气区域边界为例，上边界为6.9，则表示当燃气增加6.9℃时，冷气和壁温的测量值仍为燃气未改变之前的数值，未能同步测得变化值，从而引入试验数据误差。假设某叶片稳定状态燃气温度为900℃，平均壁温为700℃，冷气温度为300℃，冷效评估为0.333。采用常规方法，设区域上边界为6.9，则实际评估结果为0.341；若区域下边界为-7.4，则实际评估结果为0.325。同理，各温度的区域边界均可引入数据采集不同步的误差。

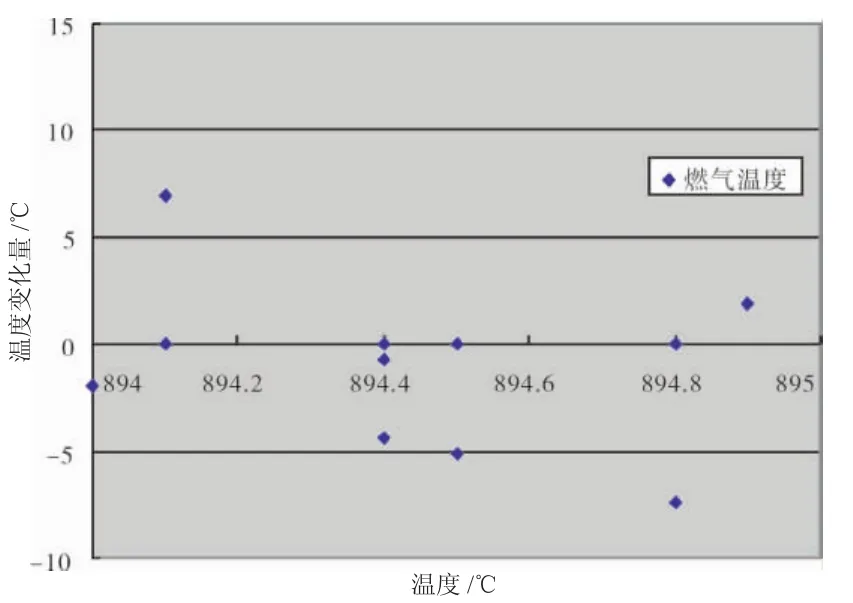
图11 燃气温度瞬时跳动分析

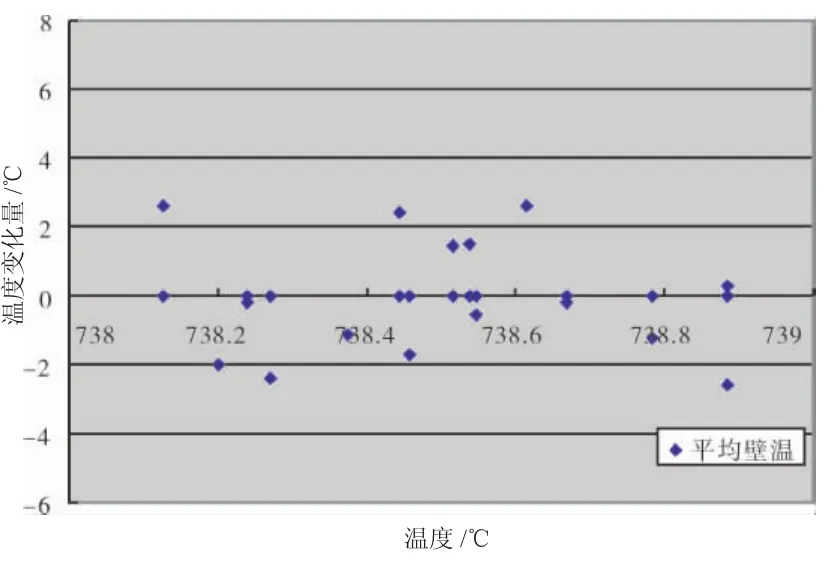
图12 冷气温度瞬时跳动分析

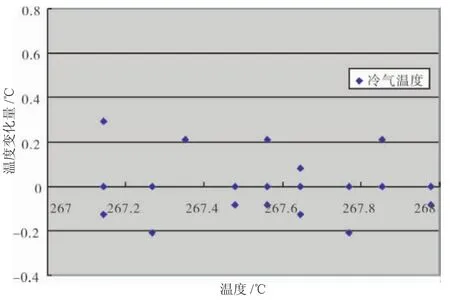
图13 平均壁温瞬时跳动分析

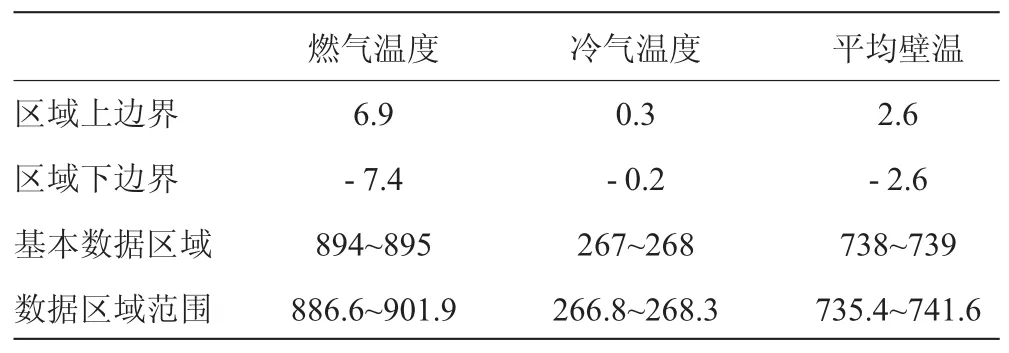
表13 个温度数据区域范围℃

本文采用的区域映射分析方法，在大数定律的基础上，分析数据瞬时跳动到最大概率密度的所有数据。采用Monte-Carlo法，用数据的频率来表示数据的概率，以数据轴代替时间轴分析数据的规律，电偶测量的不同步所引起的评估误差，将不被引入到最终的评估结果中。

2.4 Monte-Carlo分析

以燃气温度为例，选取区域映射数据886.6～901.9之间的实际测量数据为数据区域范围，使用第2.2节中所有实测数据的正态分布公式，将燃气温度的数据区域范围内的每个实测数据离散成100个温度子样，建立燃气温度的区域映射数据集。同理，建立冷气温度和平均壁温的区域映射数据集。

以此为分析基准，采用Monte-Carlo分析方法，分析冷却效果的概率密度分布形式如图14所示，具有概率特性的冷却效果介于0.232～0.265之间。

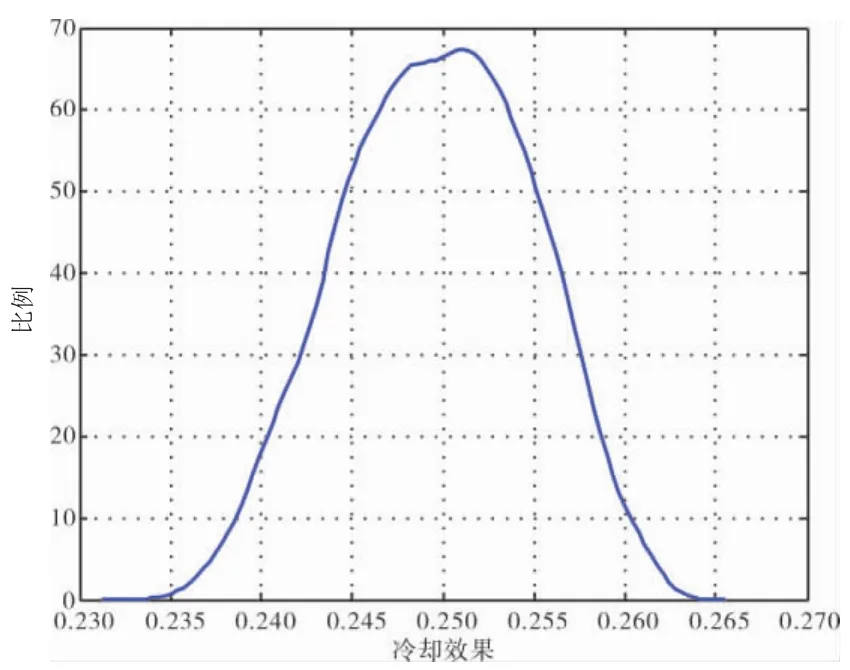
图14 冷却效果的概率密度分布

累计概率分布曲线如图15所示。横坐标为冷却效果值，纵坐标为累计概率值。以0.243冷却效果值为例，纵坐标为0.1，表示冷效值小于该值的数据占所有数据的10%。即该试验件的冷却效果不低于0.243的概率为90%。两端的试验数据表明，该叶片的冷却效果100%不会低于0.232，100%不会高于0.265。

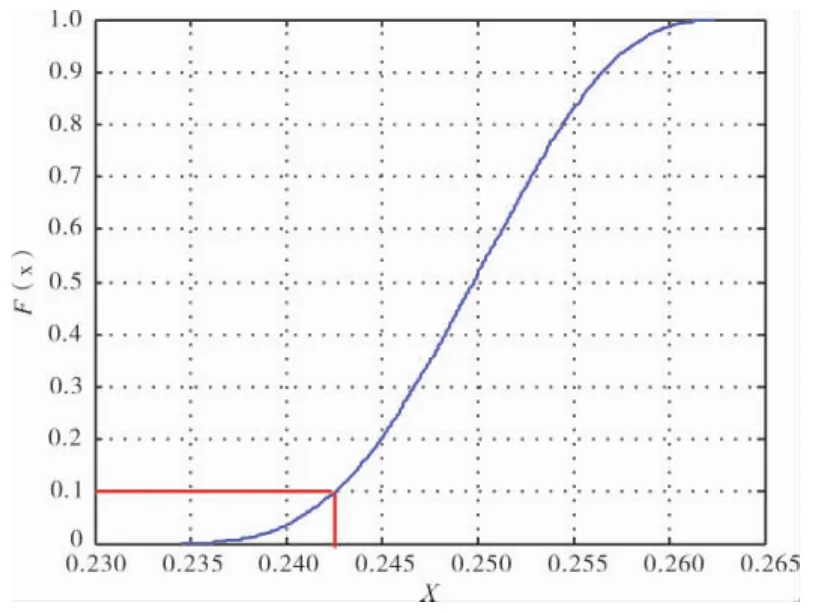
图15 冷却效果的累积概率分布

若采用常规试验方法，冷却效果的评估结果数据在采样区间内，使用该采样参数给出的冷却效果如图16所示。横坐标为冷却效果，纵坐标意义为第y次抽样。从图中可见，单次采样评估结果介于0.242～0.264之间，具有较大的分散性，考虑误差影响，也使得评估结果具有不可知性，不方便设计人员参考利用。

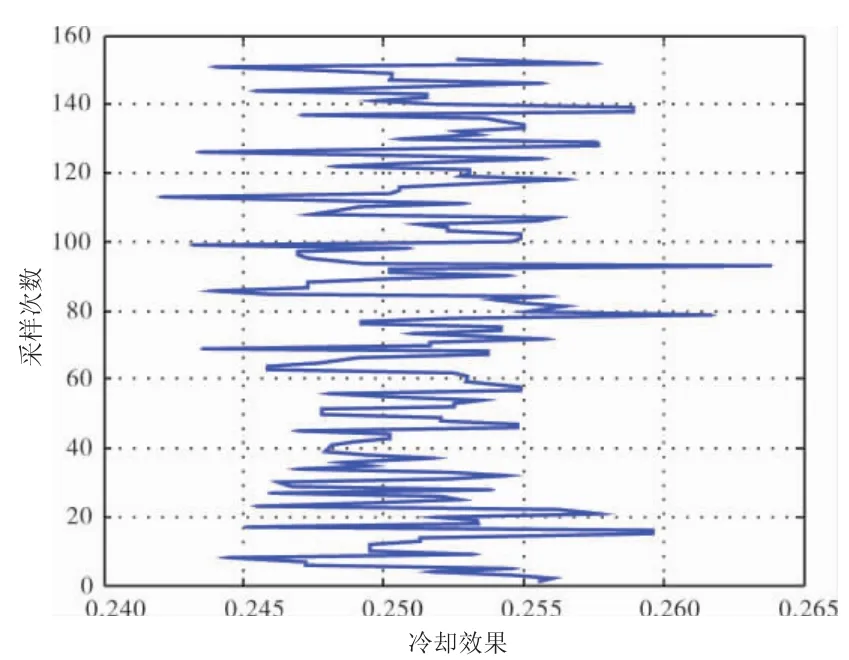
图16 样本试验数据冷却效果值

相比较于常规试验方法，区域映射Monte-Carlo法可以直观的反映分散性因素对冷却效果的影响程度，将误差直接以概率形式估计到结果评估中。如前所述，本文将每个冷却效果值都附加了一定的概率与其对应，虽然冷效值在0.232～0.265范围变化，但发生的概率更明确，相比于常规的冷却效果评估方法提供了更多信息，更方便设计人员参考。

3 结论

以确定的冷却效果评估方法，采用单次采样评估结果，直接使用试验数据，这其中包含了分散性因素和不合理数据的影响，使得结论具有不可知性。本文提出区域映射Monte-Carlo法，将概率论的数学方法引用到叶片的冷却效果评估之中，充分考虑了冷却效果试验中的各种不确定因素，并结合稳态换热的实际物理过程，去除不合理数据，将每个冷却效果值都附有一定的概率特性。通过本文的分析讨论，可以得出如下结论：

（1）区域映射Monte-Carlo法以单位长度的基准数据区域选定概率密度最大值区域，以数据瞬时最大跳动步长界定映射数据区域，相比于直接Monte-Carlo法，可得到更精确的冷却效果概率分布特性；

（2）区域映射Monte-Carlo法分析冷却效果的概率分布特性，考虑了温比、测量误差的分散性以及采集数据不同步对评估结果的影响，相比于确定性的冷却效果分析方法，具有较高的可信度；

（3）区域映射Monte-Carlo法在原有的试验基础上，只需保持试验状态一段时间，具有较强的实用性。

[1] 王利平，张靖周，姚玉.热障涂层对涡轮叶片冷却效果影响的数值研究[J].化工学报，2012，63（S1）：130-137.WANG Liping，ZHANG Jingzhou，YAO Yu.Numerical investigation on influence of thermal barrier coatings on turbine blade[J].CIESC Journal，2012，63（S1）：130-137.（in Chinese）

[2] 刘大响,程荣辉.世界航空动力技术的现状及发展动向[J].北京航空航天大学学报，2002,28（5）：490.LIU Daxiang，CHENG Ronghui.Current status and development direction of aircraft power technology in the world[J].Journal of Beijing University of Aeronautics and Astronautics，2002，28（5）：490.（in Chinese）

[3] 李佳.燃气轮机透平气膜冷却机理的实验与理论研究[D].北京：清华大学,2011.LI Jia.Experimental and theoretical research on gas turbine film cooling[D].Beijing：Tsinghua University，2011.（in Chinese）

[4] 迟重燃.气冷涡轮叶片的传热设计[D].哈尔滨：哈尔滨工业大学,2011.CHI Zhongran.Heat transferring design for air-cooling turbine blades[D].Harbin：Harbin Institute of Technology，2011.（in Chinese）

[5] 戴韧,赵志军,王宏光,等.涡轮气膜冷却流动与传热机理的基础研究[C]//赵均锷.中国动力工程学会透平专业委员会2010年学术研讨会论文集，2010：21-29.DAI Ren,ZHAO Zhijun,WANG Hongguang,et al.Basic research of turbine film cooling flow and heat transfer mechanism[C]//ZHAO June.China Power Engineering Society of Professional Committee of Turbine,the Academic Symposium on 2010，2010：21-29.（in Chinese）

[6] 王文三.涡轮中气膜孔孔型及叶片气膜冷却的流动和冷却激励研究[D].北京：中国科学院工程热物理研究所，2012.WANG Wensan.Investigation of flow and film cooling performance of new cooling hole geometry and film cooling of gas turbine[D].Beijing：Institute of Engineering Thermophysics Chinese Academy of Science，2012.（in Chinese）

[7] 朱榕川.某型低压涡轮动叶冷效试验研究[D].成都：电子科技大学，2009.ZHU Rongchuan.Experimental study about cooling efficiency of some turbine blades[D].Chengdu：University of Electronic Science and Technology，2009.（in Chinese）

[8] 周莉,张鑫,蔡元虎.非定常尾迹宽度对气膜冷却效果的影响[J].中国电机工程学报，2011,31（29）：97-102.ZHOU Li,ZHANG Xin,CAI Yuanhu.Effect of unsteady wake width on the film-cooling effectiveness for a gas turbine blade[J].Proceedings of the CSEE，2011,31（29）：97-102.（in Chinese）

[9] 姚玉.收敛缝形孔气膜冷却特性研究[D].南京：南京航空航天大学，2010.YAO Yu.Research on film cooling characteristic of converging slot hole[D].Nanjing：Nanjing University of Aeronautics and Astronautics，2010.（in Chinese）

[10] 赵永翔,王金诺,高庆.概率循环应变-寿命曲线以及评估方法[J].机械设计与研究，2000，16（4）：10-12.ZHAO Yongxiang,WANG Jinnuo,GAO Qing.Probability based cyclic strain-life curves and estimation method[J].Machine Design and Research，2000，16（4）：10-12.（in Chinese）

[11] 唐俊星,陆山.轮盘应变疲劳寿命可靠性分析方法[J].推进技术，2005,26（4）：344-347.TANG Junxing,LU Shan.Reliability analysis method for the strain fatigue life of a disk[J].Journal of Propulsion Technology，2005,26（4）：344-347.（in Chinese）

[12] 曹智顺,姚建尧,王建军.基于概率特性的航空发动机转动部件高周疲劳寿命评估技术[C]//应怀樵.现代振动与噪声技术（第九卷）.北京：航空工业出版社，2011：303-311.CAO Zhishun,YAO jiaoyao,WANG Jianjun.The techniques of life assessment about rotatable parts of aircraft engine based on probability characteristics[C]//YING Huaiqiao.Modern Technology of Vibration and Noise（Book ninth）.Beijing：Aviation Industry Press，2011：303-311.（in Chinese）

[13] 曹玉璋.航空发动机传热学[M].北京：北京航空航天大学出版社，2005：101-107.CAO Yuzhang.Heat transfer theory of aircraft engine[M].Beijing：Beijing University of Aeronautics and Astronautics Press，2005：101-107.（in Chinese）

[14] 王福保.概率论及数理统计[M].上海：同济大学出版社，1984：68-76.WANG Fubao.Probability theory and mathematical statistics[M].Shanghai：Tongji University Press，1984：68-76.（in Chinese）

[15] LIU Z M，Mavris D N.A methodology for probabilistic creep-fatigue life assessment of hot gas path components[C]//45th AIAA/ASME/ASCE/AHS/ASC Structural,Structural Dynamics and Materials Conference.Palm Springs,California：American Institute of Aeronautics and Astronautics.2004：1-11.

A New Method for Experimental Assessment of Film-Cooling Effectiveness for a Blade

CAO Zhi-shun,WANG Hong-bin,ZHANG Shu-lin,ZHANG Lian-he,XU Xiao-li
（AECC Shenyang Engine Research Institute,Shenyang 110015,China）

The experimental conclusion of the effect of film-cooling for a gas turbine has some uncertainty due to experimental error.In order to more accurately describe the experimental result and avoid that the direct use of Monte-Carlo method counts the unreasonable physical process with the assessment result more than safe,a method of regional mapping Monte-Carlo was presented.The improved regional mapping Monte-Carlo method took the internal relations of dispersion factor into account,which reduced the dispersion of results effectively.Moreover,taking the gas turbine blade as an example,the probability distribution characteristics of cooling effectiveness was obtained by using the regional mapping Monte-Carlo method.Results show that the method is of great practicability,which can be used to assess the test of film-cooling effectiveness of the gas turbine blade.

film-cooling；blade；probability distribution；test assessment；regional mapping；Monte-Carlo；aeroengine

V 232.4

A

10.13477/j.cnki.aeroengine.2016.06.010

2016-03-22基金项目：国家重大基础研究项目资助

曹智顺（1986），男，硕士，工程师，主要从事热疲劳与传热技术工作；E-mail：446383519@163.com。

曹智顺，王洪斌，张树林，等.1种叶片气膜冷却效果试验评估的新方法[J].航空发动机，2016,42（6）：61-67.CAO Zhishun，WANG Hongbin，ZHANG Shulin，et al.A new method for experimental assessment of film- cooling effectiveness for a blade[J].Aeroengine，2016,42（6）：61-67.

（编辑：栗枢）