航空发动机套齿结构配合稳健性优化设计

刘宏蕾，陈志英，周平

（北京航空航天大学能源与动力工程学院，北京100191）

航空发动机套齿结构配合稳健性优化设计

刘宏蕾，陈志英，周平

（北京航空航天大学能源与动力工程学院，北京100191）

为了更合理地设计套齿结构的配合关系，提高套齿结构配合精度，适应不对中运行工况，降低对加工误差的敏感度，研究了航空发动机套齿结构在倾角不对中的情况下的运动特点以及配合关系，并推导了含有倾角不对中的套齿结构齿侧间隙以及与之相关的套齿特征量的计算公式，对某型航空发动机的压气机轴径套齿结构进行了计算与分析。在此基础上，考虑到参数的随机性，应用果蝇优化算法对套齿结构齿侧间隙进行了稳健性优化设计。结果表明：计算公式中考虑倾角的影响能够有效地避免运动干涉和装配预应力，稳健性优化设计可以有效地避免由于倾角不对中、加工误差等参数随机因素导致齿侧间隙的设计值偏大。证明了所提出的计算和优化方法可以使套齿结构配合关系的设计更加合理，可为套齿结构设计、装配提供参考。

套齿结构；倾角不对中；齿侧间隙；果蝇优化算法；稳健性优化；航空发动机

0 引言

套齿连接结构在航空发动机中的应用非常广泛[1-2]。由于套齿结构加工安装误差、轴承不同心以及机座高低偏差等因素会使套齿存在不对中[3]的情况。在旋转机械转子故障中，不对中故障占60%以上[4]。故障使得齿间发生运动干涉以及配合状态的不稳定，从而使系统可靠性降低。不共轴时的安全系数一般降低到共轴时的1/5～1/10[5]。转子系统中套齿结构不对中普遍存在，所以在设计阶段就应对配合关系进行合理分析和设计，对于提高转子系统的稳定性具有重要意义。

套齿等机械结构装配尺寸链及配合公差的分析与设计，属于机械确定性装配关系设计范畴，在参数确定状态下装配尺寸链及各零件的公差配合关系研究，目前已经比较成熟，但近几年国内外正在发展研究一些新的装配尺寸链及配合公差的不确定分析与设计[6-9]。由于加工误差、工作环境的不确定性，使得必须要考虑参数的不确定性对套齿结构配合的影响才能更加真实地反映配合状态。

稳健性设计是由日本质量专家田口博士[10]提出的1种质量改进技术，能够有效减小产品质量波动。近年来，工程领域引入稳健性设计思想收到了很好的效果[11-13]。该设计的2项基本原则是使目标值尽可能接近最优均值且波动范围尽可能小。

本文为了更好地确定套齿配合的设计参数，研究了倾角不对中的套齿结构的运动特点、配合关系，推导了齿侧间隙等套齿特征量的计算公式，进行了稳健性优化设计，以期降低对加工误差参数随机性的敏感度。

1 套齿结构倾角不对中运动配合关系

在3点支承的方案中，由于轴和转子支承零件加工、装配误差，以及安装座位置的误差，造成压气机转子和涡轮转子2轴线彼此不对中。由于压气机后轴承靠近套齿结构，使得在这种不对中情况下，内外套齿轴线有一定倾角，且内、外套齿中心在径向重合，称为倾角不对中，如图1所示。压气机轴与涡轮轴存在倾角φ（一般φ值很小）。

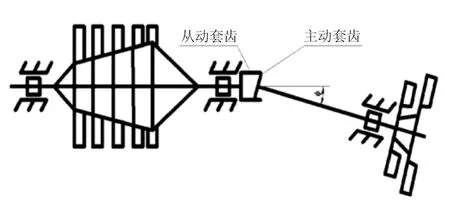
图1 压气机转子与涡轮转子倾角不对中

航空渐开线套齿齿侧既能起到驱动作用，又有自动定心的作用，在航空发动机中应用最为广泛。当内、外套齿存在不对中时，会影响套齿齿侧的最小作用间隙，应当调整配合予以补偿。为了合理地设计倾角不对中的套齿结构，需要对这种状况下套齿的运动状态和配合关系进行分析研究。

1.1 运动关系

从运动状态上来说，由于涡轮轴与压气机轴存在倾角φ，每旋转1周，外套齿都会相对于内套齿在齿长方向上作往复滑动，在圆周切线方向上绕齿中心做往复摆动。这就要求沿着齿长方向内套齿的齿长要略大于外套齿的齿长；在周向，由于存在偏角引起外套齿在内套齿往复摆动，这就需要在原来按照标准选定齿侧间隙的基础上增大设计侧隙，以免内、外套齿发生运动干涉。

1.2 配合关系

当内、外套齿完全对中时，其轴截面和A、B 2个端面如图2所示。从图中可见，内、外套齿中心线重合，并且每对齿的齿侧间隙相同。

图2 内、外套齿完全对中

如果内、外套齿存在倾角（如图3所示），并且假设此时倾角的方向是铅垂方向，即内套齿的轴线相对于外套齿在铅垂面内有个倾角φ，那么对铅垂方向上、下2部分啮合齿的齿侧间隙影响较小，但使水平方向左、右2部分的啮合齿的齿侧间隙减小较大。具有最小齿侧间隙的啮合齿会承受最大的负荷。此时处于左右象限点的啮合齿最先达到危险状态。

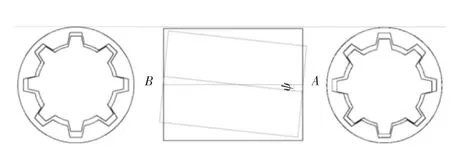
图3 内、外套齿倾角不对中

由此可知，从配合状态上来说，在垂直于倾角方向上齿侧间隙减小最为迅速。在设计侧隙时应选处于该位置的键齿进行分析和计算。为减少装配后由于该位置齿侧间隙过小以至于卡死形成预应力，一般需要加大设计间隙。

1.3 仿真验证

为了更直观地观察以上规律，应用数学建模仿真方法验证。设定内、外套齿的侧隙为0.17 mm，如图4所示。固定一端，在另外一端加1个小的垂直向下的压力，在该压力作用下，内、外套齿轴线会产生铅垂方向上的倾角。当倾斜量超过现有侧隙值时，最先发生接触的地方就会产生应力，如图5、6所示。

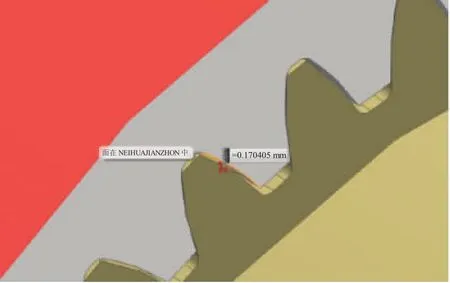
图4 侧隙为0.17 mm的套齿

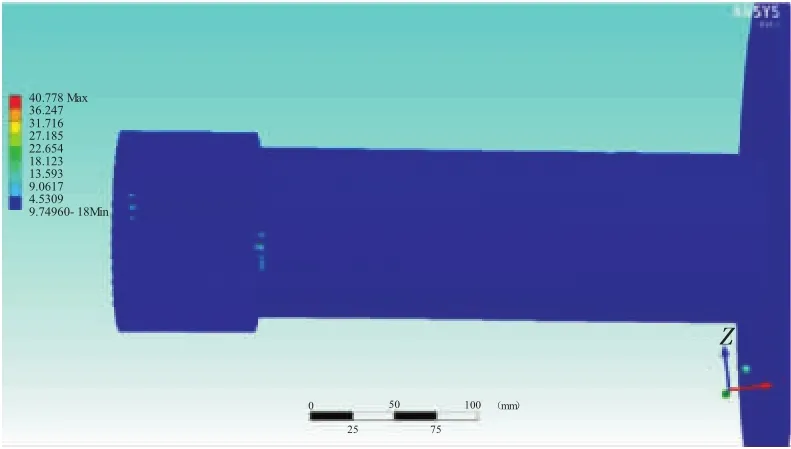
图5 外套齿等效应力分布

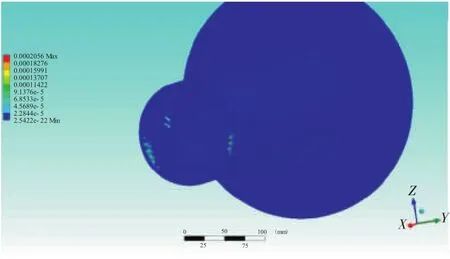
图6 内套齿等效应力分布

从图中可见，当产生沿着铅垂方向上的倾角时，在水平方向的左右两端及其附近的齿最先发生卡死的现象，产生应力，与以上分析相符。

2 套齿结构倾角不对中齿侧间隙设计

2.1 含有倾角不对中的内外套齿特征量的推导

当压气机轴与涡轮轴有偏角φ时，压气机与涡轮轴上的内、外套齿之间会产生偏斜。而在航空减速器中，轴线偏斜的情况也很常见。一般认为，当倾角小于10'时，采用直齿形联轴器；大于10'时，采用鼓形齿式联轴器。

所以在齿侧间隙设计时，除了依照截面参数和齿长查设计手册选取正常的侧隙△j之外，还应该考虑由于倾角φ导致的外套齿相对于内套齿的切向偏移量ft，进而引起侧隙的增大。

以上分析可知，在垂直于倾角方向上的键齿齿侧间隙减小最为迅速，亦即最容易达到危险状态。假设倾角是沿垂直方向的，取水平方向上的1个外齿作为研究对象，沿着分度圆柱面展开这个齿，如图7所示。其中b为齿长，S为齿厚。

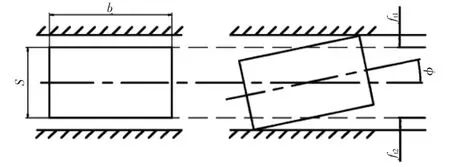
图7 啮合齿展开

将不必要的轮廓线略去，留下关键的尺寸线以及几何关系，如图8所示。

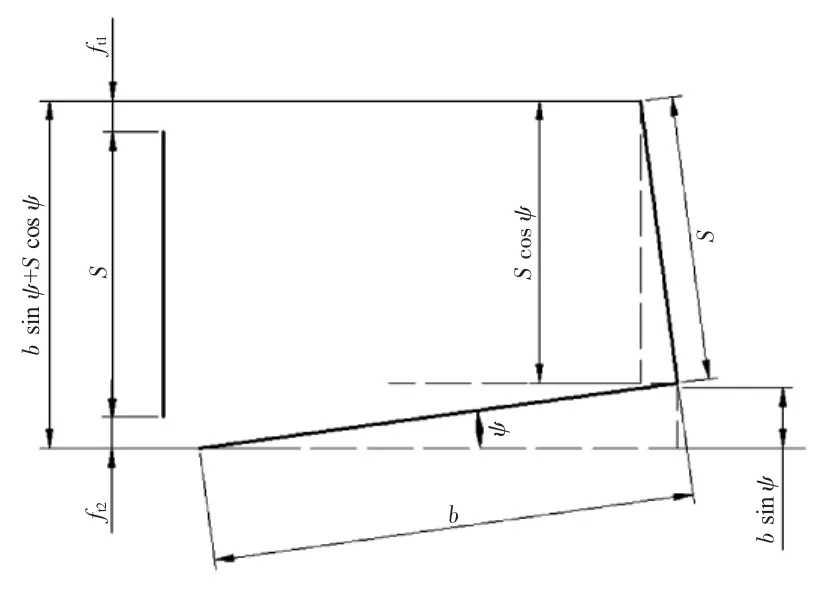
图8 关键尺寸几何关系

则由于存在倾角而需要加大的间隙值ft为

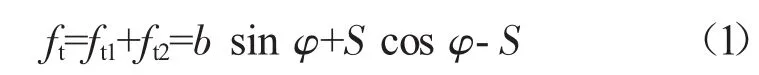
式中：ft1、ft2为相互配合的齿槽与齿厚两侧的间隙值。

最终的套齿结构齿侧间隙为

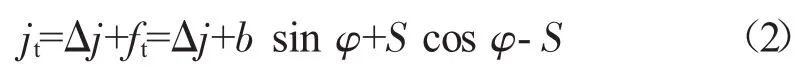
在套齿结构的设计、加工、装配过程中会涉及到一些典型的特征量：内套齿最小和最大作用齿槽宽EVmin和EVmax、外套齿最大和最小作用齿厚SVmin和SVmax、内套齿最小和最大实际齿槽宽Emin和Emax、外套齿最大和最小实际齿厚Smin和Smax。其中，内套齿最小作用齿槽宽和外套齿最大作用齿厚决定了套齿结构作用侧隙的最小值；内套齿最大作用齿槽宽和外套齿最小作用齿厚决定了套齿结构作用侧隙的最大值；内套齿最小实际齿槽宽和外套齿最大实际齿厚一般在单项检验法中使用；内套齿最大实际齿槽宽和外套齿最小实际齿厚是零件合格与否的依据。

如果不考虑倾角不对中，套齿各特征量计算公式如下：

内套齿最小作用齿槽宽

内套齿最大作用齿槽宽

外套齿最大作用齿厚

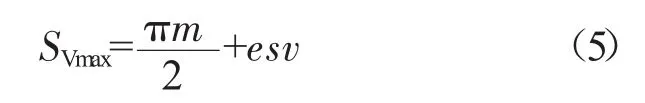
外套齿最小作用齿厚

内套齿最大实际齿槽宽

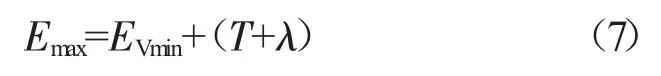
内套齿最小实际齿槽宽

外套齿最大实际齿厚

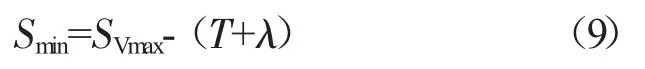
外套齿最小实际齿厚

式中：m为模数；esv为齿厚极限上偏差；λ为综合公差；T为加工公差；T+λ为总公差。

在套齿结构倾角不对中的情况下，需要加大齿侧间隙可加大齿槽宽和减小齿厚。一般情况下，考虑到航空套齿结构中内套齿的加工难度要大于外套齿，所以推导倾角不对中公式时采用移动外套齿的公差带来实现不同齿侧间隙配合。

基于以上考虑，推导出套齿各特征量计算公式：

内套齿最小作用齿槽宽

内套齿最大作用齿槽宽

外套齿最大作用齿厚

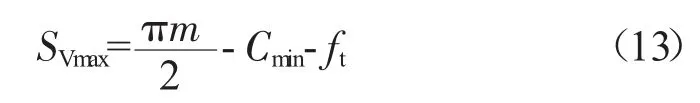
外套齿最小作用齿厚

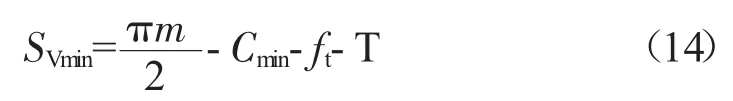
内套齿最大实际齿槽宽

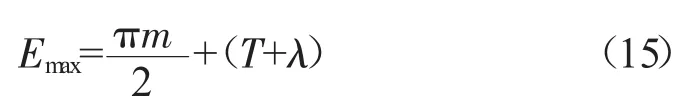
内套齿最小实际齿槽宽

外套齿最小实际齿厚

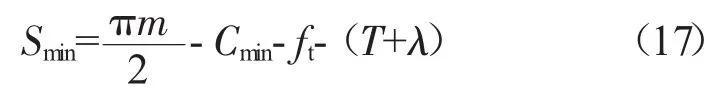
外套齿最大实际齿厚

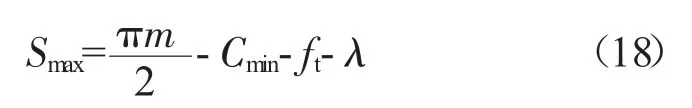
式中：Cmin为标准侧隙，根据分度圆直径以及所选取的基本偏差等级确定。

将含有倾角不对中的各装配特征量用公差带的形式表示，如图9所示。

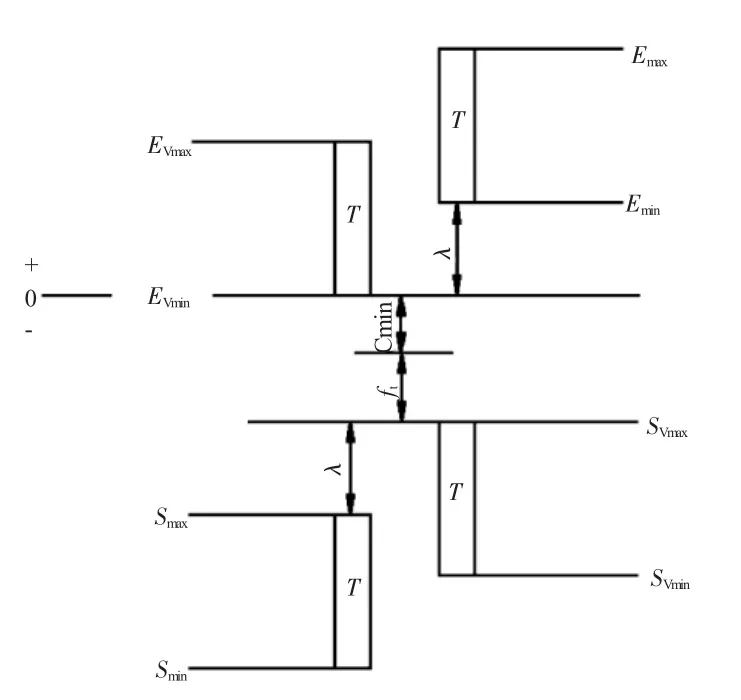
图9 倾角不对中装配特征量公差带

在航空减速器中，由于尺寸空间的限制，也会出现一些强度裕度不大的情况，考虑到内套齿的承载能力比外套齿的强，也可以用增大内套齿齿槽宽的方法来确定套齿结构倾角不对中时的特征量。

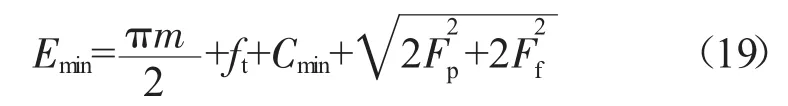
式中：Fp为齿距累积公差；Ff为齿形公差；其它特征量可按基本公式推出。

上述各式对于齿形可用于鼓形齿及2轴角偏斜大于10'情况，需要注意的是，对于鼓形套齿来说，外套齿相对于内套齿的周向摆动引起的切向位移量ftkb与直齿的不同，其计算公式为

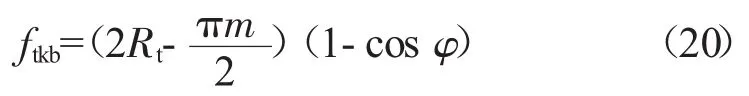
式中：Rt为鼓形齿沿齿长方向在分度圆截面上齿牙侧面轮廓曲率半径。

2.2 实例计算

某型航空发动机的压气机轴径内套齿基本参数见表1。

表1 内套齿参数

计算所需公差值按照GB/T3478.1—1995中侧隙d级和5级精度选取。具体参数见表2。

有无倾角的不对中情况的计算公式对比见表3。

假设压气机轴与涡轮轴的偏斜角φ=10'，将表1、2中的数据依次带入表3中的公式，得到套齿结构有无倾角不对中时各特征量，见表4。

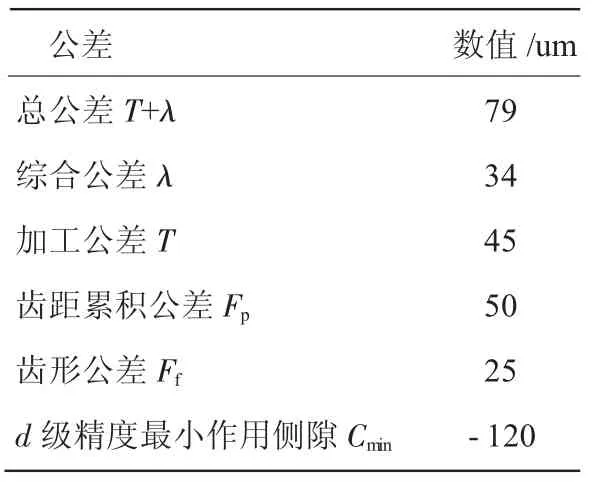
表2 按照GB/T3478.1-1995选取的公差值

表3 有无倾角不对中情况的计算公式对比

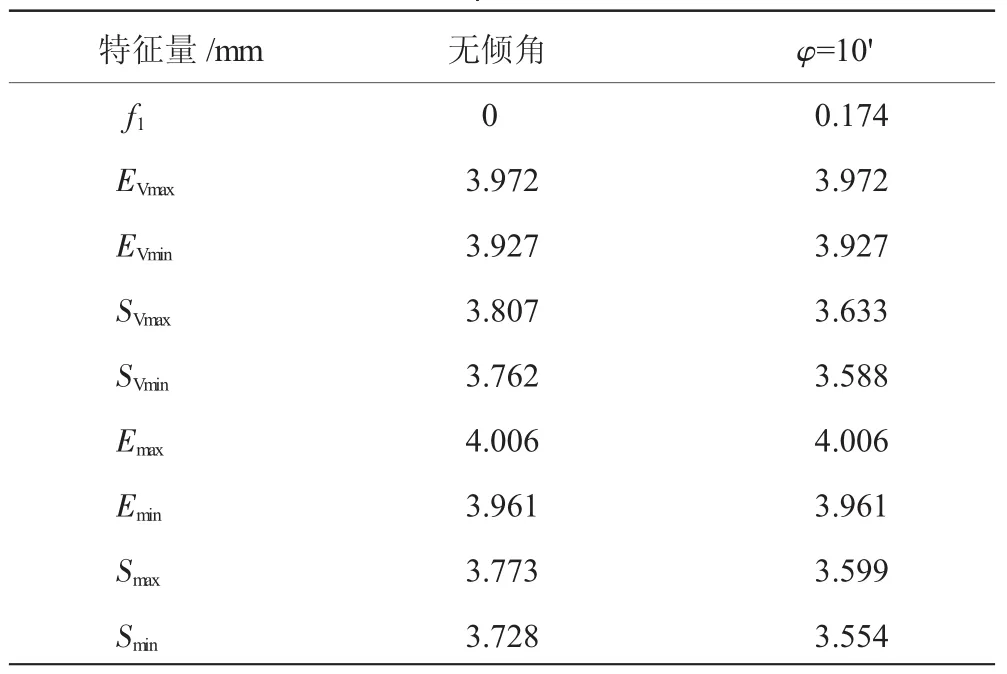
表4 无倾角与倾角φ=10'不对中时的特征量

利用UG中干涉分析功能对表中的数据进行检验。取内套齿最小作用齿槽宽EVmin与外套齿最大作用齿厚SVmax两个极限尺寸进行分析。如果2个极限尺寸所对应的套齿结构不会发生运动干涉，那么2个套齿结构取公差带内的尺寸就都不会发生运动干涉。

设置内、外套齿为连杆，以外套齿的轴线中心点为中心设置转动副，如图10所示。设定10'的角度，检查内、外套齿是否干涉，结果如图11所示。

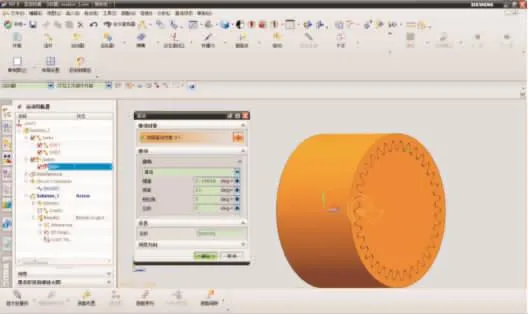
图10 检查干涉参数设置

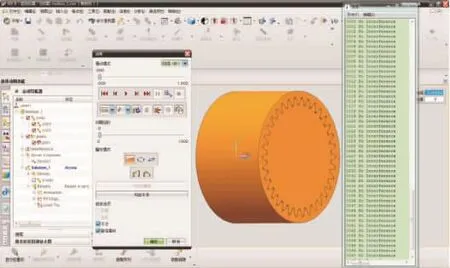
图11 检查干涉结果

将整个过程的时间步全部显示出来，列出干涉的文件显示没有干涉，采用以上方法计算出含有倾角不对中的套齿结构能很好地避免由于倾角引起的套齿间运动干涉，有效避免装配应力的产生。

3 考虑随机因素齿侧间隙稳健性优化设计

在成批生产的发动机中齿侧间隙的设计按照最大倾角设计，使得套齿结构产生过大的齿侧间隙。而最大的倾角出现的概率可能很小，按照确定性设计的套齿间隙会使设计值偏大，在套齿运行工作时，过大的齿侧间隙将会使套齿发生冲击载荷，齿侧间隙越大，冲击载荷也越大。

也就是说，基于确定性的设计是按照φ值最大来设计的，由于加工制造的原因，φ值、作用齿槽宽EV、作用齿厚SV、齿长b都是随机分布的，如果φ值取最大的情况概率极其微小，该设计就偏于保守，在套齿这种以齿侧间隙为关键技术指标的配合中是不合理的，需要对其进行优化。

果蝇优化算法（Fruit Fly Optimization Algorithm，FFOA）由中国台湾学者潘文超[14]提出，是1种基于果蝇觅食行为而推演出的寻求全局优化的新方法。将该优化算法用于工程中，可以避免优化结果陷入局部最优，而且收敛速度快[15]，所以采用果蝇优化算法对倾角不对中的套齿结构齿侧间隙进行优化。FFOA的算法流程如图12所示。

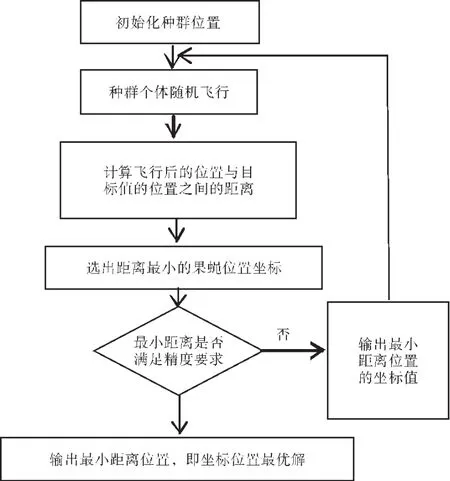
图12 FFOA的算法流程

其具体步骤为：

（1）果蝇群体位置随机初始化。

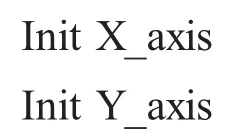
（2）给利用嗅觉搜寻食物的果蝇个体赋予随机方向与距离。

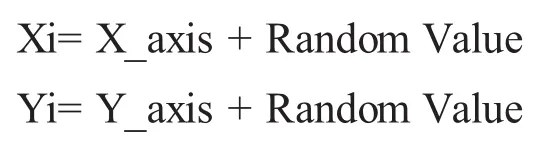
（3）由于无法知道食物位置，因此先估计与原点之距离(Dist)，再计算味道浓度判定值S，此值为距离的倒数。

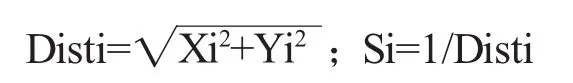
（4）将味道浓度判定值S代入味道浓度判定函数，以求出该果蝇个体位置的味道浓度(Smelli)。

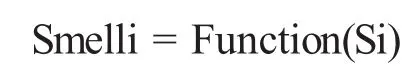
（5）找出此果蝇群体的中味道浓度最高的果蝇

（6）保留最佳味道浓度值与x、y坐标，此时果蝇群体利用视觉往该位置飞去。

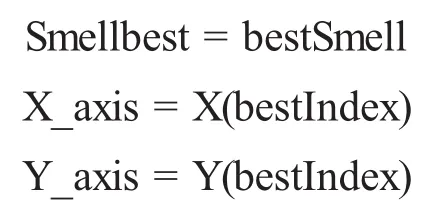
（7）进入迭代寻优，重复执行步骤（2）～（5），并判断味道浓度是否优于之前迭代味道浓度，若是则执行步骤（6）。

3.1 套齿结构配合齿侧间隙稳健性优化设计模型

加工制造误差的随机性以及倾斜角的随机性都会使侧隙设计偏大，需要优化诸如齿槽宽、外套齿的齿厚以及齿长等设计参数，使得齿侧间隙的值尽可能小。

间隙的设计需要考虑按照标准应留的齿侧间隙值，还要考虑由于倾角不对中需要预留的齿侧间隙值，除此之外再有的间隙就是由于加工制造装配误差所造成的间隙，称作额外齿侧间隙。额外齿侧间隙会严重影响套齿结构运行状态的稳定性，引起严重的冲击载荷，所以取额外齿侧间隙值为优化目标函数，希望其越小越好，其具体表达式如下

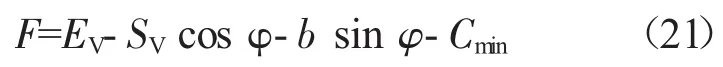
优化目标函数及约束条件如下

3.2 稳健性优化变量的选取

随机变量可以分为2类：1类是可控随机变量，在设计与制造过程中可以控制，因此能够作为待优化的参数，可以通过改变其数值来进行寻优。作用齿槽宽EV，作用齿厚SV以及齿长b的尺寸及其公差带的大小和位置都可以在设计和制造中加以控制，因此可以作为可控变量。需要说明的是，齿长b的确定和结构尺寸限制以及承载能力的设计有关，但在如公差范围这样小的尺寸范围内，可以对其优化。另外1类是不可控随机变量，该类随机变量不可以进行控制，只能作为随机输入参数而不能视为待优化参数。倾角φ受安装位置、工作环境的影响，不能对其进行控制，因此作为不可控变量。假设以上随机变量均为正态分布。考虑到航空套齿结构的精度要求以及加工工艺所能达到的精度水平，各变量具体情况见表5。

表5 稳健性优化随机变量

3.3 优化过程和结果分析

利用FFOA对考虑随机因素的套齿结构配合齿侧间隙进行稳健性优化设计，优化前后的装配关键特征量的对比见表6。

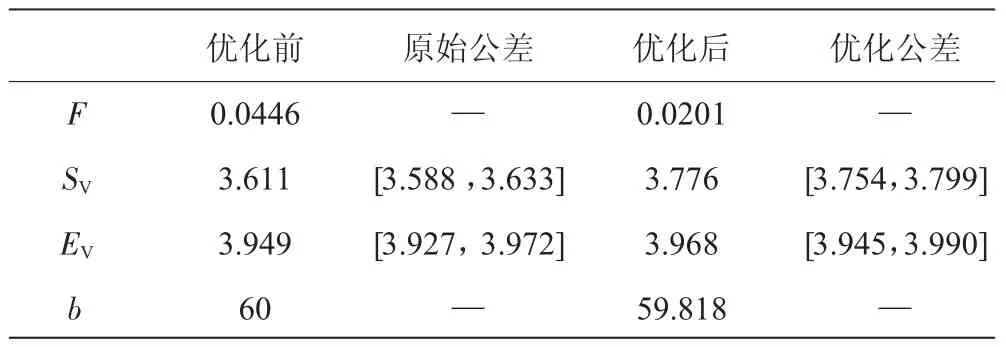
表6 优化前后数据对比mm

从表中可见，相对于优化之前，优化后的公差带长度没有变化，均为0.045 mm，表明加工制造费用和之前一样。而额外齿侧间隙值由之前的0.0446 mm减小到0.0201 mm，减小了55%，所以进行稳健性优化的效果非常明显，可以在现有加工水平的基础上提高套齿结构齿侧间隙对抗参数波动干扰能力。

4 结论

在套齿结构配合关系设计之初就应该充分考虑转子系统不对中所引起的额外齿侧间隙，计算公式中考虑倾角的影响能够有效地避免运动干涉和装配预应力。

采用果蝇优化算法对齿侧间隙进行稳健性优化设计，可以有效地避免由于倾角不对中以及工作环境、加工误差等参数随机因素的存在导致齿侧间隙的设计值偏大，使设计更加合理。

以上对于转子系统中存在倾角不对中的套齿结构特征量的计算方法，以及考虑到参数的随机性特点，对齿侧间隙稳健性优化设计的方法可以为套齿结构设计、装配提供参考，在实际的设计、装配、使用过程中需要重视。

[1] 陈光.航空发动机结构设计分析[M].北京：北京航空航天大学出版社，2014：349-393.CHEN Guang.Structural design analysis of aeroengine[M].Beijing：Beihang University Press,2014：349-393.（in Chinese）

[2] 航空发动机设计手册总编委会.航空发动机设计手册（第13分册）：减速器[M].北京：航空工业出版社，2001：251-275.Aeroengine Design Manual General Editorial Board.Aeroengine design manual(album 13)：deceleration device[M].Beijing：Aviation Industry Press，2001：251-275.（in Chiense）

[3] 王聪梅.航空发动机典型零件机械加工[M].北京：航空工业出版社，2014：128-185.WANG Congmei.Mechanical processing of typical parts of aeroengine[M].Beijing：Aviation Industry Press,2014：128-185.（in Chinese）

[4] 刘占生.转子系统联轴器不对中研究综述[J].汽轮机技术,2007，49（5）：321-325.LIU Zhansheng.Research on the coupling misalignment of rotor system[J].Steam Turbine Technology,2007,49（5）：321-325.（in Chinese）

[5] 刘永福.航空发动机构造[M].北京：国防工业出版社，1995：194-201.LIU Yongfu.Aviation engine construction[M].Beijing：National Defense Industry Press，1995：194-201.（in Chinese）

[6] 王瑜.公差稳健优化设计的研究[J].计算机集成制造系统，2007，13(11)：2081-2085.WANG Yu.Research on robust optimal design of tolerance[J].Computer Integrated Manufacturing System,2007，13(11)：2081-2085.（in Chinese）

[7] 阎艳,余美琼,王国新,等.平面尺寸链公差分析算法研究[J].北京理大学学报，2011,31（7）：799-802.YAN Yan,YU Meiqiong,WANG Guoxin,et al.Study on the algorithm of plane dimension chain tolerance analysis[J].Journal of Beijing University of Science and Technology，2011，31（7）：799-802.（in Chinese）

[8] Siva K M，Islam M N，Lenin N,et al.Optimum tolerance synthesis for complex assembly with alternative process selection using Lagrange multiplier method[J].International Journal of Engineering，2010，3（4）：380-402.

[9] Jinn T T.Robust optimal-parameter design approach for tolerance design problems[J].Engineering Optimization,2010，42（12）：1079-1093.

[10] Taguchi G.Taguchi on robust technology development：bringing quality engineering upstream[M].New York：ASME Press，1993：1-15.

[11] 陈立周.稳健设计[M].北京：机械工业出版社，1999：2-67.CHEN Lizhou.Robust design[M].Beijing：Mechanical Industry Press，1999：2-67.（in Chinese）

[12] Ghanmi S，Bouazizi M L，Bouhaddi N.Robustness of mechanical systems against uncertainties[J].Finite Elements in Analysis and Design，2007，43（9）：715-731.

[13] 程远胜，钟玉湘，游建军.概率及非概率不确定性条件下结构鲁棒设计方法[J].工程力学，2005，8（4）：10-14.CHENG Yuansheng，ZHONG Yuxiang，YOU Jianjun.Probabilistic and non-probabilistic uncertainties under the condition of robust design of structure[J].Engineering Mechanics，2005，8（4）：10-14.（in Chinese）

[14] Pan W T.A new fruit fly optimization algorithm：taking the financial distress model as an example[J].Knowledge Based Systems，2012，26(2)：69-74.

[15] 周平，白广忱.基于神经网络与果蝇优化算法的涡轮叶片低循环疲劳寿命健壮性设计[J].航空动力学报，2013，28（5）：1013-1018.ZHOU Ping，BAI Guangchen.Based on neural network in drosophila and optimization algorithm of the turbine blade low cycle fatigue life of robust design[J].Journal of Aerospace Power，2013，28（5）：1013-1018.（in Chinese）

Robust Optimization Design of Aeroengine Mating Spline Structure

LIU Hong-lei，CHEN Zhi-ying，ZHOU Ping
（School of Energy and Power Engineering，Beihang University，Beijing 100191 China）

In order to design the matching relationship of spline structure,improve the matching precision,adapt to the misalignment of the working conditions and reduce the sensitivity of the mismachining tolerance,the characteristics of spline structure of the aircraft engine casing in the dip angle and the matching relationship were studied.The calculation formula of the tooth flank clearance and the related characteristics of the spline structure were derived.On this basis,the optimal design of the algorithm for the optimization of the tooth flank clearance of the sleeve was designed.Results show that the calculation formula considered angle influence can effectively avoid the movement interference and assembly prestressing force,and robust design and optimization can effectively reduce tooth side gap due to the influence of random parameters such as angle misalignment and mismachining tolerance.It is proved that the calculation and optimization method can make the design more reasonable,which can provide reference for the design and assembly of spline structure.

spline structure;angle misalignment;tooth side gap;fruit fly optimization algorithm;robust optimization;aeroengine

V 232.9

A

10.13477/j.cnki.aeroengine.2016.06.007

2016-05-21基金项目：国家自然科学基金（51275024）资助

刘宏蕾（1990），男，硕士，研究方向为航空发动机结构强度可靠性和动态装配；E-mail：15933906068@163.com。

刘宏蕾，陈志英，周平.航空发动机套齿结构配合稳健性优化设计[J].航空发动机，2016,42（6）：44-50.LIUHonglei，CHENZhiying，ZHOUPing.Robustoptimizationdesignofaeroenginematingsplinestructure[J].Aeroengine，2016,42（6）：44-50.

（编辑：栗枢）