针对局部非线性问题的混合坐标模态综合法

王陶，何欢，2，＊，陈国平，2

1．南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016 2．南京航空航天大学 振动工程研究所，南京 210016

针对局部非线性问题的混合坐标模态综合法

王陶1，何欢1，2，＊，陈国平1，2

1．南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016 2．南京航空航天大学 振动工程研究所，南京 210016

非线性动力系统模型的计算效率问题是结构动力学领域中的重要研究课题。提出了一种针对局部非线性问题的混合坐标自由界面子结构模态综合方法。根据局部非线性系统的特点，将结构按照线性部分与非线性部分进行分割。线性部分子结构可以通过模态坐标转换到模态空间。在对线性部分进行减缩的过程中考虑了剩余柔度的影响，并通过构造一组与低阶模态关于系统矩阵加权正交的向量组，解决了子结构含有刚体模态时剩余柔度矩阵无法计算的问题。非线性部分子结构则保留原有的物理坐标。通过界面协调关系，采用自由界面方法得到系统混合坐标综合方程。最后，通过数值算例验证了所提出方法的有效性。

局部非线性；混合坐标；自由界面；模态综合；协调关系

随着工程结构的日益复杂化，研究者越来越重视结构的非线性特征对结构动力学行为的影响。其中有一类结构系统在变形过程中只有局部呈现出明显的非线性特征，而其余部分仍保持线性，这就是所谓的局部非线性问题。例如，飞行器着陆冲击过程［1］就是一个典型的局部非线性问题。对于这类局部非线性问题，如果采用有限元法（FEM）对其直接进行建模，所得到的动力学方程为非线性动力学方程，当对其进行动力学分析时，其计算量将会数倍于线性模型。于是，在保证计算精度的基础上如何有效降低此类问题的计算规模就成为许多研究者关注的一个重点。其中，子结构模态综合法就是一种减缩结构自由度数目的经典方法。

子结构模态综合法最早由 Hurty［2］于1965年提出，文中主要讨论了无阻尼线性结构的模型减缩方法。Goldman［3］和 Macneal［4］针对比例阻尼结构提出了相应的改进。随后，很多学者在提高计算精度、处理复杂界面条件等方面也进行了大量的研究工作［5－7］。在不断的改进与发展之后，逐渐形成了目前针对线性结构的较为完备的理论体系。近年来，越来越多的研究者开始将子结构模态综合法应用于更为复杂的结构动力学问题中去，例如在一般黏性阻尼结构振动分析［8］、大型复杂结构模型修正［9］、结构不 确定性 分析［10－11］等问题中模态综合法都表现出了很好的应用前景。

对于局部非线性问题来说，非线性主要存在某一小范围区域内，其他大部分结构可以认为仍然符合线弹性假设。利用这个特点，很多学者也开始把子结构模态综合法的思想引入局部非线性结构的动力学分析中，通过对模型进行减缩来提高其计算效率。Clough－Wilson［12］最先提出将子结构模态综合法应用于大型局部非线性结构的动力学分析当中。郝淑英等［13］采用子结构模态综合法建立了非线性连接元组成的连接子结构的减缩模型，并通过渐进法求解了系统的一次近似定常解。文献［14－16］采用子结构模态综合法对转子系统的局部非线性问题进行了研究。Verros和Natsiavas［17］用自由界面模态综合法对机车的非线性动力学问题进行了相关研究。Kawamura等［18］提出了一种针对多自由度非线性系统的子结构模态综合法，通过计算结果可以看出在子结构没有刚体模态时，其方法具有较高的计算精度。Saito等［19］采用 Craig－Bampton方法对裂纹结构的非线性受迫振动进行了动响应分析。Praveen Krishna和Padmanabhan［20］采用不同模型减缩方法对局部非线性系统进行了分析，并对这些减缩方法的有效性进行了讨论。上述研究在采用自由界面子结构模态综合法对局部非线性问题进行分析时，没有考虑剩余柔度的影响，且在子结构存在刚体模态时的计算精度较差。

针对上述问题本文提出了一种混合坐标自由界面子结构模态综合法。为了提高计算精度，考虑了剩余柔度的影响，并解决了含刚体模态时的系统剩余柔度矩阵无法直接求解的问题。在综合过程中对线性部分进行模态减缩，非线性部分仍保持物理坐标下的形式，所以系统依然保留了原有的非线性特性。通过界面协调条件将转换到模态坐标下的线性子结构与物理坐标下的非线性子结构组装得到由模态坐标与物理坐标混合表示出的综合方程。由于综合模型规模的减小使得其计算效率可以得到很大的提高。

1 线性子结构模型减缩

根据局部非线性系统的特点，将系统按照线性结构与非线性结构进行划分，将线性子结构记为子结构a，则其结构动力学方程可表示为

式中：Ma、Ca和Ka∈Rn×n分别为子结构a的质量矩阵、阻尼矩阵和刚度矩阵；ua和fa∈Rn×1分别为广义位移向量和载荷向量。通过特征值分析，容易计算出线性子结构较低阶的l阶模态Φla。需要指出的是，由于考虑自由界面形式，所以这里Φla可能包含有刚体模态。

1．1 构造加权正交向量集

假设存在矩阵φa∈Rn×（n－l）满足

使得

先给定线性无关的n－l个向量

结合式（2）和式（3）可解得

由此可得

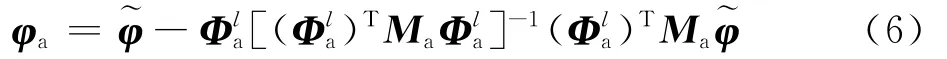
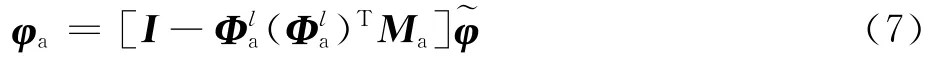
1．2 剩余柔度矩阵与界面协调方程

定义Φa＝［Φlaφa］，则子结构的物理坐标可以表示为

利用Φa可将式（1）转换为

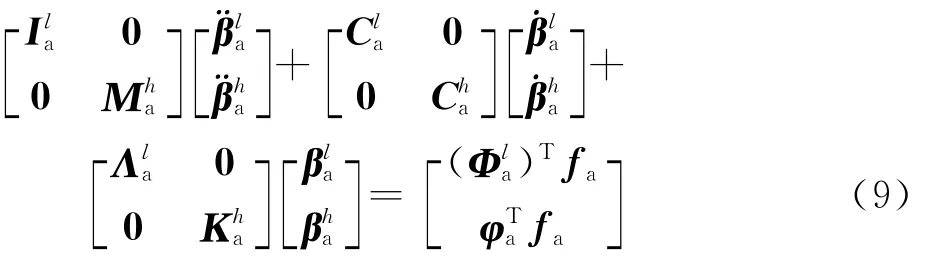
将式（9）展开，其高阶模态坐标所对应的方程可以表示为

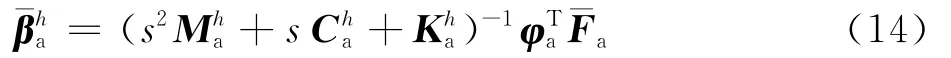
将式（13）进行Laplace变换后，可得式中：s为复变量；F珚a为fa在s域中的表示形式。

将式（14）进行泰勒展开，并取其一阶近似，再进行反Laplace变换后，可得

这实际上相当于保留了刚度项的影响。

将式（15）代入式（8），展开后可得

式中：

式中：

其中：Ga∈Rn×n为剩余柔度矩阵。由于φa为构造出来的等效高阶模态，φa中并未包含刚体模态。所以式（9）与式（12）中的仅与高阶模态有关，为可逆矩阵。因此，当子结构存在刚体模态时，仍可以通过式（17）来求解剩余柔度矩阵。

假设子结构的交界面上有m个自由度，将广义物理坐标进行分块处理，按照内部坐标与界面坐标写为

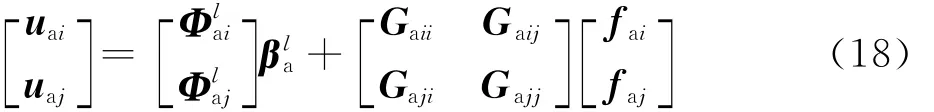
式中：uaj为子结构界面自由度所对应的位移；uai为子结构内部自由度所对应的位移；fai为结构内部自由度上所受到的外力；faj为界面力为界面位移所对应的界面模态；为内部位移所对应的内部模态。

将式（18）展开，则界面坐标可以表示为

2 非线性子结构动力学方程

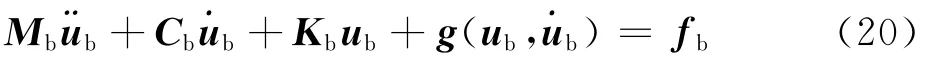
将非线性子结构记为子结构b，其动力学方程可表示为式中：Mb、Cb和Kb分别为子结构b线性部分的质量矩阵、阻尼矩阵和刚度矩阵；g（ub， ub）为其非线性项。

类似地，将其按照内部自由度与界面自由度进行分块，可以写为

整理式（21），子结构b的界面位移可以表示为

3 局部非线性系统的混合坐标综合方程

仅考虑简单的界面情况，即界面外载荷为零，界面上不添加集中质量和弹簧，所以界面位移的连续性条件与载荷协调关系可写为

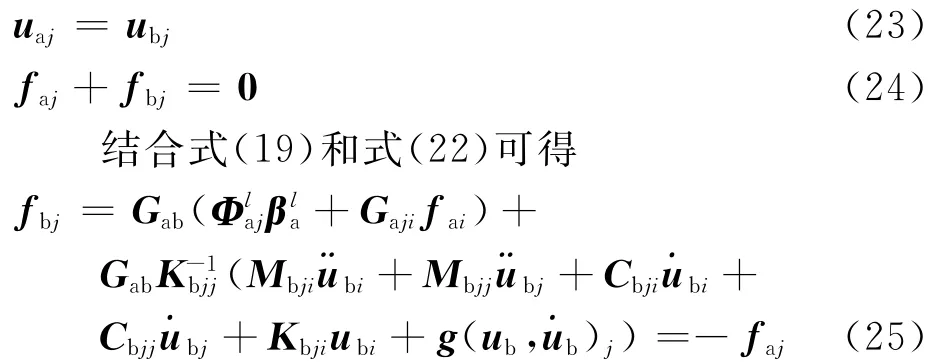
式中：

将式（25）代入式（9）与式（21），可以得到结构的综合方程为

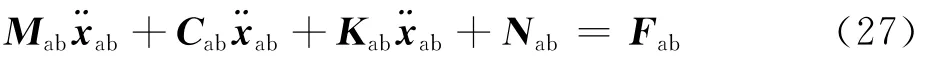
式中：

定义P＝ （Φlaj）TGabK－1bjj，则式（28）～式（30）中的相关参数表达式为

4 数值算例

4．1 算例1

如图1所示为一个考虑阻尼的十自由度弹簧质量块系统（阻尼器没有出现在图中，但认为阻尼器平行于弹簧存在于系统中），其中最右侧与固定端连接的弹簧具有非线性特性，这里非线性力可以表示为fnonlinear＝k（x＋εx3）。将系统在第10个质量块处分割为两个子结构，记左侧结构为子结构1，其仅具有线性特性；记右侧结构为子结构2，其具有非线性特性。系统的相关参数为

式中：γj为Reyleigh阻尼常数；ε为小参数。

图1 十自由度局部非线性系统Fig．1 A ten－degree－of－freedom system with localised nonlinearities

分别提取子结构1的2、4、6和8阶低阶模态进行综合，对非线性系统所对应的派生系统进行特征值分析。表1比较了综合模型与原模型计算得到的固有频率，其中r为保留的低阶模态数。从表1中可以看出，随着提取的低阶模态数目的增加，通过本文方法计算所得到的固有频率的精度也逐渐提高。

假设一个周期外力作用于m9，采用谐波平衡法对非线性系统进行频响分析。其中周期力可表示为：f9＝F9cos（ωt＋θ），F9＝500N，其中ω为激励频率，θ为激励与响应之间的相位差。若只考虑一阶谐波，则根据谐波平衡法此时系统的稳态响应可以表示为：xj＝Ajcos（ωt）（j＝1，2，…，l＋1），其中Aj为响应幅值。将周期力及响应的表达式代入综合方程，通过比较等式两边的一次谐波项系数，就可以得到相应的幅频特性曲线表达式。

如图2所示，为系统第一阶固有频率所对应的幅频特性曲线。从图中可以看出，系统的幅频特性曲线有着明显的跳跃现象，且随着提取的低阶模态数目的增加，通过模态综合法计算所得的幅频特性曲线也逐渐趋近于原始结构的计算结果。

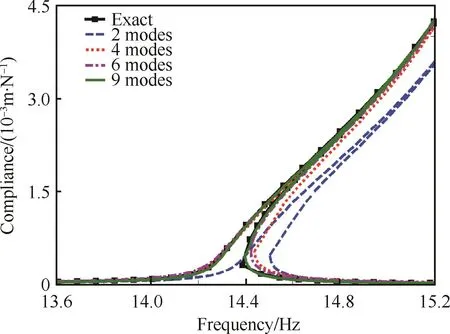
图2 m10的幅频特性曲线比较Fig．2 Comparison of frequency－amplitude curves of m10

4．2 算例2

考虑如图3所示的具有局部非线性的飞机着陆问题的结构系统。将其分为机身部分与起落架部分。其机身部分为线性区域，作为子结构a，通过用空间梁单元对其进行建模，共有69个梁单元，414个自由度。机身部分的结构阻尼假设为：C＝αM＋βK，α与β为Rayleigh阻尼常数。机身结构的总质量为9 195．75kg。机身模型的其他参数如表2所示。

对于具有非线性特性的起落架系统（如图3中红色圆圈所示为其安装位置）通过引入非线性弹簧阻尼单元来进行模拟。此部分作为子结构b。起落架内部的缓冲力可以表示为fnonlinear（u， u）＝kbu＋γkbu3＋c1u。其中u为沿起落架轴线方向的位移。采用集中质量单元模拟起落架系统的质量，每个起落架的等效质量记为m1。起落架模型的参数如表3所示。

以图3所示结构在平衡位置处的微振动为基准。在此基础上提取通过模态分析得到的子结构a的前10、20、30和40阶低阶模态（包含前6阶刚体模态）进行模态综合。表4分别给出了完全有限元模型与模态综合模型的计算结果。

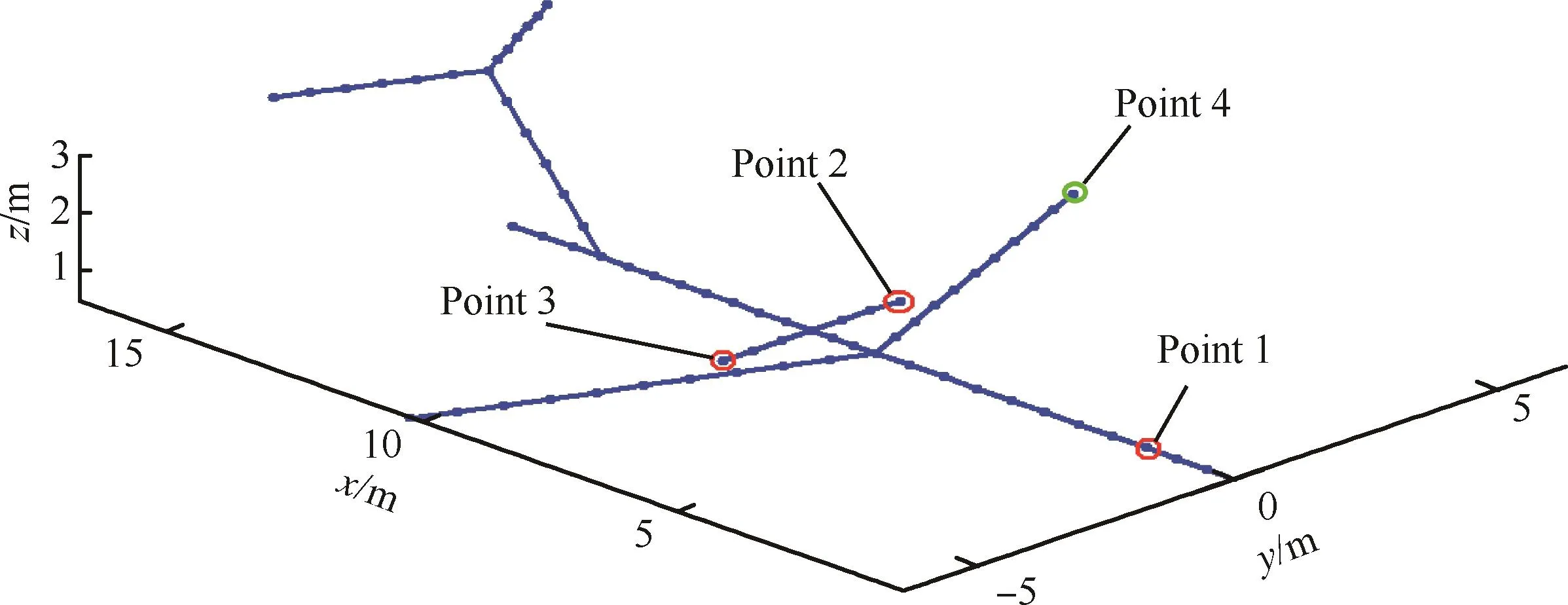
图3 飞机总体结构模型Fig．3 Model of fuselage structure

表2 机身模型参数Table 2 Parameters of fuselage model

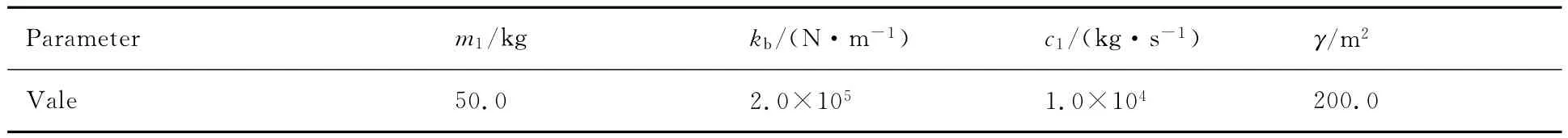
表3 起落架模型参数Table 3 Parameters of landing gears model

表4 模态综合模型与完全有限元模型的固有频率比较Table 4 Comparison of natural frequencies between synthesis models and full FE model

图4 固有频率误差对比Fig．4 Comparison of errors for natural frequencies

图4所示为保留前20、30和40阶低阶模态所计算得到的前20阶固有频率的误差对比。从图4中可以看出，通过本文方法所计算得到的固有频率有较高的精度，当提取低阶模态数目达到40阶时，计算的误差都在1%以内。考虑机身在z方向上初始速度为－5m／s时的动力学时域响应分析。分别采用子结构综合模型和完全有限元模型进行计算，仿真分析时间为3s。采用本文提出的模态综合法，分别保留线性子结构的前10、20、30和40阶低阶模态用于模态综合。

图5给出了图3结构上Point 1、Point 2与Point 4沿z方向上的位移响应曲线比较。从图5可以看出，位移响应与完全有限元模型计算结果吻合得很好。随着采用的低阶模态数目的增加，运用模态综合所计算出的位移响应都与完全有限元模型给出的计算结果趋于一致。

图5 Points 1，2，4沿z方向的位移响应Fig．5 Displacement response along z direction at Points 1，2，4

定义CPU time ratio为Ts／Tf，其中Ts为综合模型计算所需CPU计算时间，Tf为完全有限元模型计算所需CPU计算时间。从表5中可以看出，综合模型的计算效率有了非常大的提高。

表5 综合模型与完全有限元模型计算时间比较Table 5 Comparison of CPU time consumed between synthesis models and full FE model

5 结 论

1）在综合过程中考虑了剩余柔度的影响，通过构造一组与低阶模态关于系统矩阵加权正交的向量组，解决了子结构具有刚体位移时剩余柔度矩阵无法求解的问题。采用自由界面综合方法得到了混合坐标下的模态综合方程。

2）利用谐波平衡法对一多自由度弹簧质量块系统进行了频响分析。计算结果表明本文方法可以有效地处理局部非线性系统频域下的振动特性问题，这为进一步研究诸如分岔等非线性行为提供了一种实用方法。

3）对飞机着陆问题进行了时域响应分析。数值分析结果表明，利用本文方法得到的减缩模型能够高效准确地求解局部非线性系统的动响应问题。合理保留一定数量的低阶模态后，综合模型不仅具有良好的计算精度，更重要的是从本质上改善了局部非线性系统动响应问题的计算效率。

［1］ 董威利，刘莉，周思达．含局部非线性的月球探测器软着陆动力学模型降阶分析［J］．航空学报，2014，35（5）：1319－1328．DONG W L，LIU L，ZHOU S D．Model reduction analysis of soft landing dynamics for lunar lander with local nonlinearities［J］．Acta Aeronautica et Astronautica Sinica，2014，35（5）：1319－1328（in Chinese）．

［2］ HURTY W C．Dynamic analysis of structural systems using component modes［J］．AIAA Journal，1965，3（4）：678－785．

［3］ GOLDMAN R L．Vibration analysis by dynamic partitioning［J］．AIAA Journal，1969，7（6）：1152－1154．

［4］ MACNEAL R H．A hybrid method of component mode synthesis［J］．Computers and Structures，1971，1（4）：581－601．

［5］ RUBIN S．Improved component－mode representation for structural dynamic analysis［J］．AIAA Journal，1975，13（8）：995－1006．

［6］ QIU J B，YING Z G，WILLIAMS F W．Exact modal synthesis techniques using residual constraint modes［J］．International Journal for Numerical Methods in Engineering，1997，40（13）：2475－2492．

［7］ BENFIELD W A，HRUDE R F．Vibration analysis of structures by component mode substitution［J］．AIAA Journal，1971，9（7）：1255－1261．

［8］ HE H，WANG T，CHEN G P，et al．A real decoupled method and free interface component mode synthesis methods for generally damped systems［J］．Journal of Sound and Vibration，2014，333（2）：584－603．

［9］ PAPADIMITRIOU C，PAPADIOTI D C．Component mode synthesis techniques for finite element model updating［J］．Computers and Structures，2013，126（1）：15－28．

［10］ CHENTOUF S A，BOUHADDI N，LAITEM C S．Robustness analysis by aprobabilistic approach for propagation of uncertainties in a component mode synthesis context［J］．Mechanical Systems and Signal Processing，2011，25（7）：2426－2443．

［11］ MENCIK J M．Model reduction and perturbation analysis of wave finite element formulations for computing the forced response of coupled elastic systems involving junctions with uncertain eigenfrequencies［J］．Computer Methods in Applied Mechanics and Engineering，2011，200（45－46）：3051－3065．

［12］ CLOUGH R W，WILSON E L．Dynamic analysis of large structural systems with local nonlinearity［J］．Computer Methods in Applied Mechanics and Engineering．1979，17（18）：107－129．

［13］ 郝淑英，陈予恕，张琪昌，等．连结子结构在非线性动力学分析中的应用［J］．天津大学学报，2001，34（3）：295－299．HAO S Y，CHEN Y S，ZHANG Q C，et al．Application of link substructure to nonlinear dynamic system analysis［J］．Journal of Tianjin University，2001，34（3）：295－299（in Chinese）．

［14］ 华军，许庆余，张家忠．挤压油膜阻尼器－滑动轴承－转子系统非线性动力特性的数值分析及实验研究［J］．航空学报，2001，22（1）：42－45．HUA J，XU Q Y，ZHANG J Z．Numerical and experimental study on nonlinear dynamic behavior of the fluid film bearing－rotor system with squeeze film damper［J］．Acta Aeronautica et Astronautica Sinica，2001，22（1）：42－45（in Chinese）．

［15］ IWATSUBO T，SHIMBO K，KAWAMURA S．Nonlinear vibration analysis of a rotor system using component mode synthesis method［J］．Archive of Applied Mechanics，2003，72（11－12）：843－855．

［16］ 吕延军，虞烈，刘恒．非线性转子－轴承系统的动力学特性及稳定性［J］．机械强度，2004，26（3）：242－246．LV Y J，YU L，LIU H．Dynamic characterstics and stability of nonlinear rotor－bearing system［J］．Journal of Mechanical Strength，2004，26（3）：242－246 （in Chinese）．

［17］ VERROS G，NATSIAVAS S．Ride dynamics of nonlinear vehicle models using component mode synthesis［J］．Journal of Vibration and Acoustics，2002，124（3）：427－434．

［18］ KAWAMURA S，NAITO T，ZAHID H M，et al．Analysis of nonlinear steady state vibration of a multi－degreeof－freedom system using component mode synthesis method［J］．Applied Acoustics，2008，69（7）：624－633．

［19］ SAITO A，CASTANIER M，PIERRE C，et al．Efficient nonlinear vibration analysis of the forced response of rotating cracked blades［J］．Journal of Computational ＆ Nonlinear Dynamics，2006，4（1）：53－63．

［20］ PRAVEEN KRISHNA I R，PADMANABHAN C．Improved reduced order solution techniques for nonlinear systems with localized nonlinearities［J］．Nonlinear Dynamics，2011，63（4）：561－586．

Component mode synthesis method based on hybrid coordinates for structure with localised nonlinearities

WANG Tao1，HE Huan1，2，＊ ，CHEN Guoping1，2
1．State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China 2．Institute of Vibration Engineering Research，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China

The calculation efficiency of nonlinear dynamic system has become increasingly important in the structural dynamics field．A hybrid coordinates component mode synthesis method is proposed in this paper for the structure with localised nonlinearities．According to its feature，generally，the system is divided into the linear component and nonlinear component．The equations of the linear component can be transformed into the modal coordinates by its linear vibration modes．In order to improve the accuracy，the residual flexibility attachment matrix of the system is introduced．And by constructing the weighted－orthogonal vector sets which have weighted－orthogonal relationship with the lower retained modes，the residual flexibility attachment matrix is obtained without using inverse of the stiffness matrix．The equations of the nonlinear component are kept as their original form．The synthesis equations which are expressed by hybrid coordinates are derived in terms of compatibility conditions at the interface．Finally，applications of the proposed methods to the numerical examples demonstrate that the present method is computationally effective．

localised nonlinearities；hybrid coordinates；free interface；component mode synthesis method；compatibilityconditions

2015－09－09；Revised：2015－12－08；Accepted：2015－12－28；Published online：2016－01－20 13：47

URL：www．cnki．net／kcms／detail／11．1929．V．20160120．1347．002．html

s：National Natural Science Foundation of China（11472132）；the Fundamental Research Funds for Central Universities（NS2014002）；Priority Academic Program Development（PAPD）of Jiangsu Higher Education Institutions

V215；O322；TB123

A

1000－6893（2016）09－2757－09

10．7527／S1000－6893．2015．0360

2015－09－09；退修日期：2015－12－08；录用日期：2015－12－28；网络出版时间：2016－01－20 13：47

www．cnki．net／kcms／detail／11．1929．V．20160120．1347．002．html

国家自然科学基金（11472132）；中央高校基本科研业务费专项资金（NS2014002）；江苏高校优势学科建设工程

＊通讯作者．Tel．：025－87138242 E－mail：hehuan＠nuaa．edu．cn

王陶，何欢，陈国平．针对局部非线性问题的混合坐标模态综合法［J］．航空学报，2016，37（9）：27572－765．WANG T，HE H，CHEN G P．Component mode synthesis method based on hybrid coordinates for structure with localised nonlinearities［J］．Acta Aeronautica et Astronautica Sinica，2016，37（9）：27572－765．

王陶 男，博士。主要研究方向：复杂结构动力学。Tel．：025－84892197

E－mail：wangtao813619＠163．com

何欢 男，博士，副教授，硕士生导师。主要研究方向：复杂结构动力学、飞行器回收系统动力学。

Tel．：025－87138242

E－mail：hehuan＠nuaa．edu．cn

陈国平 男，博士，教授，博士生导师。主要研究方向：复杂结构动力学与控制。

Tel．：025－84892142

E－mail：gpchen＠nuaa．edu．cn

＊Corresponding author．Tel．：025－87138242 E－mail：hehuan＠nuaa．edu．cn