模块化六自由度机器人运动学标定与实验研究①

王殿君 王超星 陈 亚 彭文祥 关似玉

(*北京石油化工学院机械工程学院 北京 102617) (**北京化工大学机电工程学院 北京 100029)



模块化六自由度机器人运动学标定与实验研究①

王殿君②*王超星③**陈 亚*彭文祥*关似玉*

(*北京石油化工学院机械工程学院 北京 102617) (**北京化工大学机电工程学院 北京 100029)

针对自主研发的模块化六自由度轻载搬运机器人，使用激光跟踪仪并采用直接标定法进行了运动学标定与实验研究。采用D-H法构建了机器人连杆坐标系和机器人运动学模型，并运用微分变换的方法建立误差模型。通过激光跟踪仪测量机器人末端位置，将其与运动学模型求解得到的机器人末端位置进行比较，验证了误差模型的正确性。然后将误差模型计算得到的机器人连杆参数误差在机器人控制系统软件中进行修正。最后利用激光跟踪仪测量机器人的关节转角间隙误差，将误差值转换成脉冲数并在软件中进行补偿。机器人运动学标定实验表明，使用激光跟踪仪进行连杆参数误差补偿和关节转角间隙误差补偿可以明显的减小绝对定位误差，绝对定位误差降低了69.6%，定位精度有了明显的提高。

模块化六自由度机器人， 运动学标定， 激光跟踪仪， 误差模型， 定位精度

0 引 言

机器人运动学参数标定方法分为基于模型的运动学参数标定方法和基于非模型的运动学参数标定方法。目前对机器人运动学参数标定的研究主要集中在基于模型的运动学参数标定。基于模型的运动学参数标定方法一般包括四个过程：建模、测量、识别和补偿[1]。一般采用D-H法构建运动学模型，采用激光跟踪仪进行测量，采用最小二乘优化求解模型，最后在控制系统中对运动学参数直接修正。运动学参数标定方法具有操作性强、效率高、效果好等优点，被广泛应用于机器人运动学参数标定。除了上述的标定方法之外，还可以用由Zhuang[2]及Schröer[3]等提出的CPC(complete and carametrically continuous cinematic model)方法进行建模，但是这种建模方法强调参数的完整性与连续性，运算复杂。测量方法也可以利用三坐标测量仪进行测量，其优点是测量精度高，但是占用空间面积较大，成本高且不易移动[4]。参数识别算法除了最小二乘法之外还有Levenberg-Marquardt算法，这种算法具有很强的局部收敛性能，但是在相同收敛条件下所需要的内存较大且未考虑误差分布情况[5-7]。

本文首先运用D-H法构建机器人连杆坐标系并建立运动学模型，然后运用微分变换的方法建立误差模型，通过激光跟踪仪进行运动学标定实验，最后分别对机器人连杆参数误差和关节转角间隙误差进行补偿。

1 模块化六自由度轻载搬运机器人运动学模型的建立

1.1 机器人三维模型

模块化六自由度轻载搬运机器人为六自由度串联关节式结构，其结构原理图如图1所示。机器人的6个关节均为转动关节，L、U、B、T关节做俯仰运动，S、R关节做回转运动。第6个关节末端预留适配接口，以满足不同的安装需要(如手爪)。

图1 六自由度轻载搬运机器人结构原理图

1.2 建立机器人连杆坐标系及运动学模型

采用D-H法构建机器人连杆坐标系，可得到4个连杆参数，分别是连杆长度ai-1、连杆扭角αi-1、连杆距离di和关节转角θi[8]。机器人连杆的D-H 坐标系如图2所示。

图2 六自由度轻载搬运机器人连杆坐标系

依据机器人机构设计和建立的连杆坐标系，确定机器人的连杆参数，如表1所示。

表1 六自由度轻载搬运机器人连杆参数表

其中:α2=424, α3=375, d2=147, d5=111.5, d6=120。

(1)

由式(1)可推导出，六自由度轻载搬运机器人各个相邻连杆坐标系的变换矩阵如下：

将得到的6个连杆坐标变换矩阵连乘得

(2)

式(2)为六自由度轻载搬运机器人的正运动学方程。通过运动学方程可得到机器人末端在空间中的位置坐标px、py、pz，末端在空间的姿态nx、ny、nz、ox、oy、oz、ax、ay、az。

2 建立模块化六自由度轻载搬运机器人误差模型

本文的机器人误差模型是采用微分变换的思想建立的。机器人相邻连杆的齐次变换矩阵是由连杆长度a,连杆偏距d,连杆转角α及连杆夹角θ 4个连杆参数来确定的，由相邻连杆的齐次变换矩阵联乘可以确定机器人末端的位姿。这里设连杆参数与机器人末端位姿之间的关系式为

P=F(a,d,α,θ)

(3)

而实际加工和装配过程中存在着误差，导致装配好的机器人连杆参数与理论值存在偏差，设连杆参数a、d、α、θ存在的误差分别为Δa、Δd、Δα、Δθ，则机器人在基座坐标系中的末端位姿P′与理论末端位姿P,也存在误差ΔP′，而

P′=F(a+Δa,d+Δd,α+Δα,θ+Δθ)

(4)

ΔP=P-P′

(5)

由于机器人实际的连杆参数与理论值之间的误差相对较小，可以简化成相应的线性方程：

(6)

对于模块化六自由度搬运机器人，式(6)中的∂a分别表示∂a1、∂a2、∂a3、∂a4、∂a5、∂a6，同理，∂d、∂α、∂θ也各包含六个参数。

机器人的末端位置累积误差近似方程可表示为

(7)

将式(7)用矩阵形式表达为

ΔP=JδΔδ=P-P′

(8)

式中ΔP=(ΔPx，ΔPy，ΔPz)T， P为机器人末端中心点的理论坐标值，P′为实际坐标点，Jδ为误差系数矩阵，其具体可表示为

(9)

Δδ为机器人的连杆参数误差矢量，即：

Δδ=(Δa0…Δa5, Δd1…Δd6, Δα0…Δα5,

Δθ1…Δθ6)T

(10)

式(8)可以用机器人末端位置误差求解连杆参数误差，也可以由连杆参数误差得到机器人末端位置误差[9,10]。

3 模块化六自由度轻载搬运机器人运动学标定

标定实验平台由激光跟踪仪、计算机、模块化六自由度轻载搬运机器人、实验场地构成。所采用的激光跟踪仪是美国发如公司生产的FARO-ION型号仪器，空间测量精度可达0.049mm，距离测量精度为4μm+0.8μm/m，角度测量精度为20μm+5μm/m，测量精度远远大于机器人的精度。

模块化六自由度轻载搬运机器人运动学标定采用直接标定法。标定原理为：首先，利用激光跟踪仪测得机器人各关节在不同旋转角度下末端靶心在基座坐标系下的实际位置，利用Matlab软件和建立的运动学方程求解出末端靶心的理论位置，实际位置和理论位置相减得出机器人末端靶心的位置误差。其次，将各关节旋转角度代入到式(9)得出误差矩阵，根据式(8)可以得出机器人连杆参数修正值，并在机器人控制系统软件中进行修正。最后，根据激光跟踪仪测得机器人关节转角的反向间歇误差，将其换算成脉冲数，得到关节转角反向间歇误差补偿值，并在机器人控制系统软件中进行补偿[11,12]。标定实验的流程图如图3所示。

图3 标定实验流程图

3.1 验证误差模型

(1) 首先，通过机器人控制软件操作机器人，并以表2中所示的10组关节角取值运动，每组关节角测5次机器人末端位置，将5次测得的平均值作为机器人末端实际坐标值；其次，将10组关节角分别代入式(3)中，得到了机器人末端的理论位置，计算得到机器人末端位置误差ΔP′。

(2) 将10组关节角θ分别和激光跟踪仪测得的机器人连杆参数误差值构成的连杆参数误差矢量Δδ代入误差模型ΔP=JδΔδ中，计算得到理论误差值ΔP′。

(3) 将得到的机器人末端位置实际误差值与理论误差值进行比较，结果如表2所示。

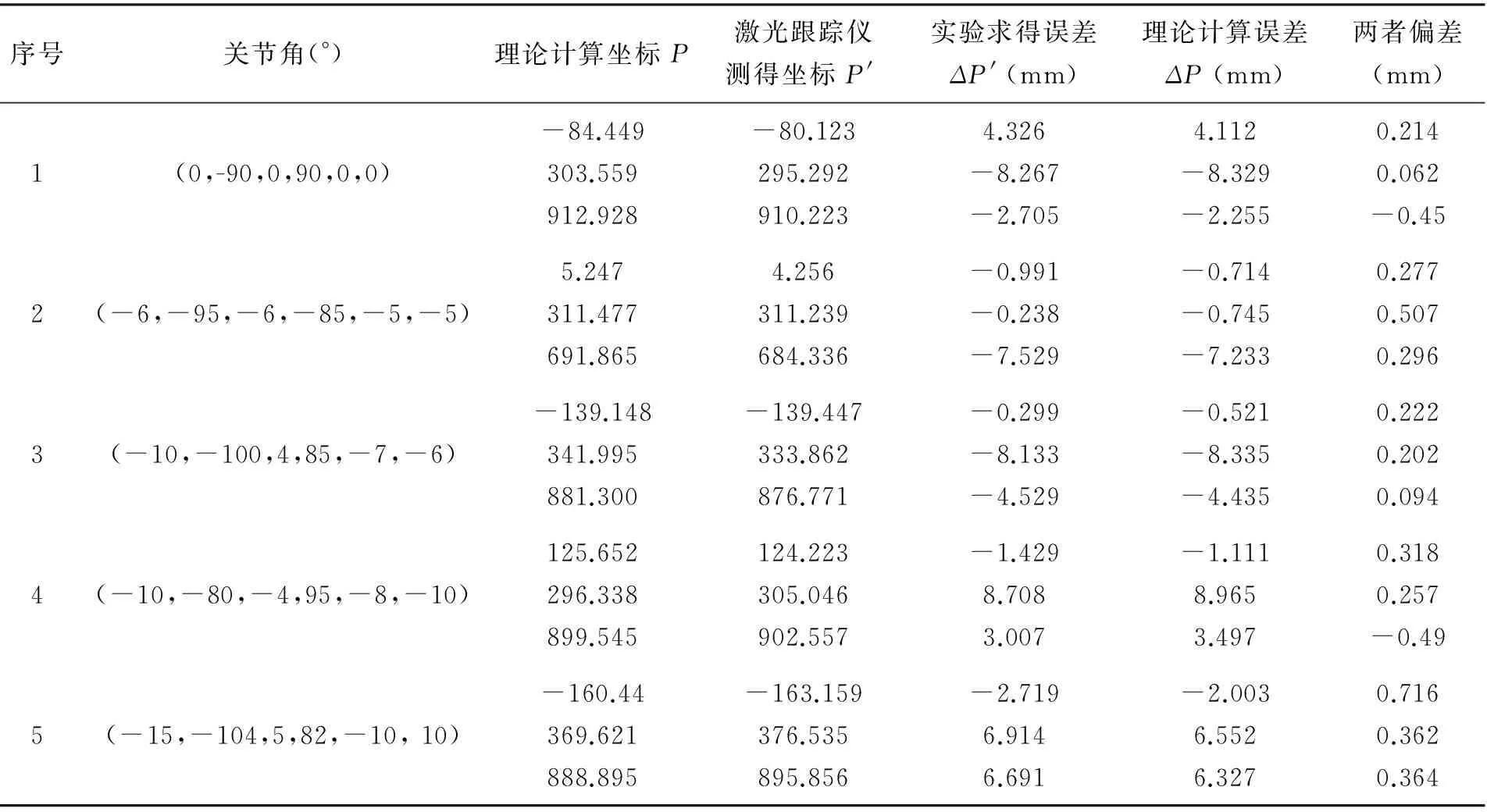
表2 误差对比结果

(续表2)

将表2的误差对比结果在二维曲线图中表示，如图4所示。可知通过激光跟踪仪实际测得的机器人绝对定位误差与通过误差模型计算得出的绝对定位误差相差较小，从一定程度上证明了该误差模型的正确性，因此可以用该模型求出的绝对定位误差代表机器人的实际绝对定位误差。

图4 标定实验前后绝对定位误差对比曲线

3.2 机器人定位误差补偿

利用表2中实验得到的机器人末端位置误差和误差系数矩阵，采用最小二乘法进行优化，求得机器人连杆参数误差，将连杆参数误差在控制系统软件中进行修正，进行标定实验。

通过标定实验得到标定后绝对定位误差。通过表2计算得到标定前的绝对定位误差，在同一组关节角下得到的标定前后绝对定位误差的比较结果如表3所示。

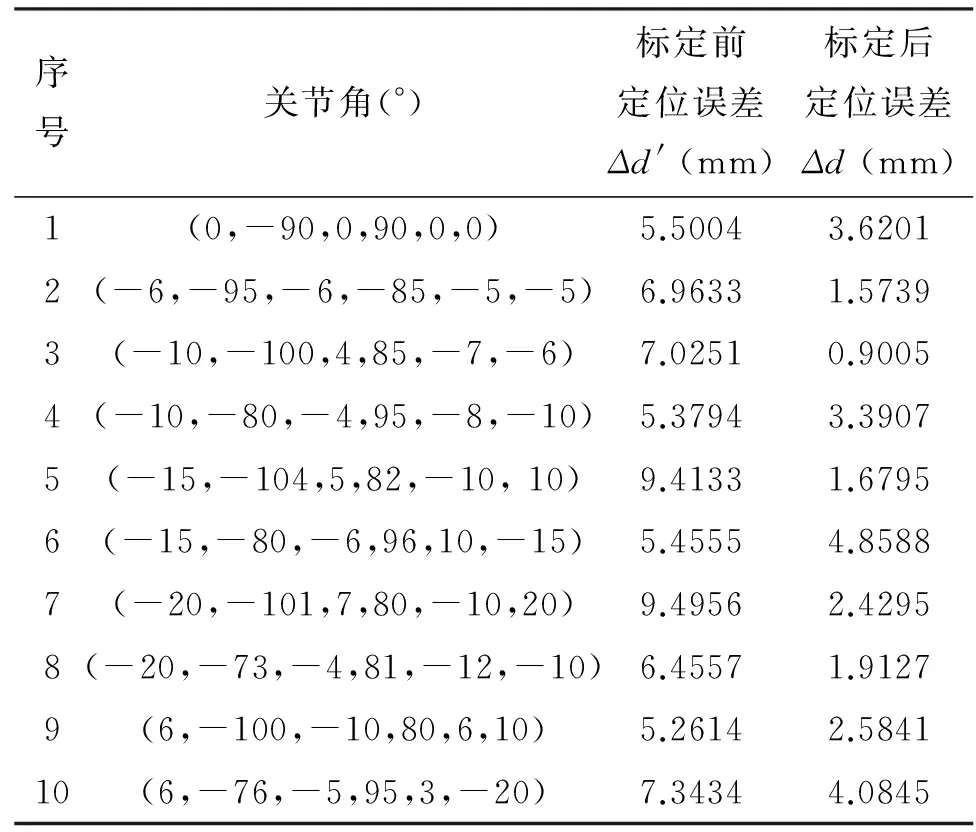
表3 标定前后绝对定位误差

将表3中的绝对定位误差对比结果在二维曲线图中表示，如图5所示。补偿前绝对定位误差最大值为9.495mm，平均值约为6.83mm，补偿后绝对定位误差最大值为4.858mm，平均值约为2.703mm，机器人定位精度提高了近50%。

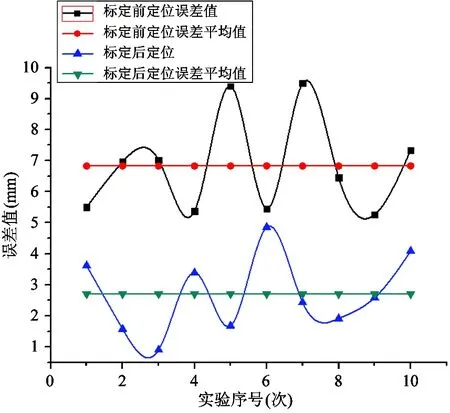
图5 标定实验前后绝对定位误差对比曲线

3.3 机器人间歇误差补偿

以一轴为例进行机器人关节的间隙补偿实验。选取关节转动范围为0°～40°，以4度为步长，控制机器人关节运动，通过激光跟踪仪测量关节实际转动角度，将关节实际转动角度换算成实际发送脉冲数，并与编码器反馈的脉冲数作对比，将差值在上位机软件中进行直接补偿，再次测量脉冲补偿后的激光跟踪仪实测角度，以一轴为例的机器人转动角度测试结果如表4所示。

表4 脉冲补偿前后的单轴关节转角误差

由表4中数据可以得出，进行间隙误差补偿之后的实测的机器人转角与理论转角相差较小。由于机器人的每个轴都可能存在间歇误差，还需要对其他5个轴进行间歇误差补偿。各个轴完成间歇误差补偿后进行标定实验，得到标定后绝对定位误差，由表3可知标定前的绝对定位误差，在同一组关节角下得到的标定前后绝对定位误差的比较结果如表5所示。

表5 标定前后绝对定位误差

将表5中的绝对定位误差对比结果在二维曲线图中表示，如图6所示。补偿前绝对定位误差最大值为4.858mm，平均值为2.703mm，补偿后绝对定位误差最大值为2.884mm，平均值为1.205mm，机器人精度提高了40.6%。

图6 标定实验前后绝对定位误差对比曲线

4 结 论

本文以自主研发的模块化六自由度轻载搬运机器人为平台，采用直接标定法对提高机器人的绝对定位精度问题进行了运动学标定技术研究。

(1) 采用D-H法建立了运动学模型，运用微分变换的方法建立了误差模型，基于激光跟踪仪进行了模块化六自由度轻载搬运机器人的运动学标定实验，对机器人的连杆参数误差和关节转角间隙误差进行了补偿。

(2) 标定实验表明，采用直接标定法利用激光跟踪仪对机器人进行运动学标定可以减小机器人的绝对定位误差，绝对定位误差的最大值由补偿前的9.495mm减小到2.884mm，最小值由补偿前的5.261mm减小到0.0347mm，平均值由补偿前的6.83mm减小到1.205mm，绝对定位误差降低了69.6%，搬运机器人定位精度有了明显的提高，已满足实际生产的需求。

(3) 通过运动学标定，搬运机器人的绝对定位精度达到设计要求，但是还没有达到理想的结果。因为在标定过程中只考虑的机器人的连杆参数误差和反向转角间歇误差，而忽略了热变形和力变形等因素的影响。因此，搬运机器人的绝对定位精度还能够进一步的提高，在后续的研究中将进一步探索。

[1] 叶声华, 王一, 任永杰等. 基于激光跟踪仪的机器人运动学参数标定方法. 天津大学学报, 2007, 40(2): 202-205

[2] Zhuang H Q, Roth Z S. A complete and parametrically continuous kinematicmodel for robot manipulators.IEEEtransactiononroboticsandautomation, 1992，8(4): 451-463

[3] Schröer K, Albright S L, Grethlein M. Complete, minimal and model-continuous kinematic models for robot calibration.RoboticsandComputer-IntegratedManufacturing, 1997, 13(1): 7385

[4] Liu Z, Yang J, Wang M. Research of kinematics parameter calibration for robot manipulator based on measuring method. In: Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation, Chengdu, China, 2009. 2735-2740

[5] 刘振宇, 陈英林, 曲道奎等. 机器人标定技术研究. 机器人, 2002, 24(5): 447-450

[6] Calafiore G, Indri M, Bona B. Robot dynamiccalibration:ptimal excitationtrajectories and experimental parameter estimation.JournalofRoboticSystem, 2001,18(2): 55-68

[7] Watanabe A, Sakakibara S, Ban K, et al. A kinematic calibration method for industrial robots using autonomous visual measurement.CIRPAnnals-ManufacturingTechnology, 2006, 55(1): 1-6

[8] 冯玉倩. 7R型工业机器人本体结构设计及其运动学标定. 北京：北京化工大学, 2013

[9] Ouyang J F, Yan Y G. Research of measuring accuracy of laser tracker system.ProceedingsofSPIE-TheInternationalSocietyforOpticalEngineering, 2006, 6280:62800T-62800T-6

[10] 龚星如, 沈建新, 田威等. 工业机器人的绝对定位误差模型及其补偿算法. 南京航空航天大学学报, 2012, 44(s1): 60-64

[11] James H B, Su P, Zhao C Y, et al. Use of a commercial laser tracker for optical alignment.ProceedingsofSPIE-TheInternationalSocietyforOpticalEngineering, 2007, 6676

[12] 任永杰, 邾继贵, 杨学友等. 利用激光跟踪仪对机器人进行标定的方法. 机械工程学报, 2007, 43(9): 195-200

Kinematic calibration and experimental study of a modular six-DOF robot

Wang Dianjun*, Wang Chaoxing**, Chen Ya*, PengWenxiang*, Guan Siyu*

(*College of Mechanical Engineering, Beijing Institute of Petrochemical Technology, Beijing 102617) (**College of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing 100029)

A laser tracker and a direct calibration method were applied to the kinematic calibration and experimental study of an indepently developed light load robot with six DOF (degree of freedom). The D-H method was used to construct the robot’s coordinate system of connecting rod and kinematic model, and its error model was established by using the method of differential transformation. The end position of the robot was measured by the laser tracker, and the measured value was compared to that obtained through the kinematic model to verify the correctness of the error model. Then, the error of the robot’s connecting rod parameter error calculated by the error model was modified in the robot’s control system software. Finally, the robot’s joint angle gap error was measured by the laser tracker, and the error value was transformed into the pulse number for compensation by software. The experiment on robot kinematic calibration shows that the absolute positioning error can be significantly reduced through the compensation of connecting rod parameter and the error compensation of the rotation angle of joint clearance with the laser tracker. The absolute positioning error was reduced by 69.6% and the location accuracy was significantly improved.

modular six-DOF robot, kinematic calibration, laser tracker, error model, location accuracy

10.3772/j.issn.1002-0470.2016.06.008

①863计划(2012AA041402)资助项目。

2016-03-06)

②男，1973年生，博士，硕士生导师，教授；研究方向：光电检测与机器人应用技术；E-mail: wangdianjun@bipt.edu.cn

③通讯作者，E-mail: 867023045@qq.com