基于差分进化的时变信道最大似然估计算法①
丁青锋 邱 翔
(华东交通大学电气与自动化工程学院 南昌 330013)
基于差分进化的时变信道最大似然估计算法①
丁青锋②邱 翔
(华东交通大学电气与自动化工程学院 南昌 330013)
研究了隧道环境下的通信信道估计。针对隧道环境的地铁列车与轨旁设备之间无线通信中无线传输信道快速变化的特点,提出了一种采用元胞差分进化(DE)方法实时获取时变信道的有效信道长度的新型最大似然(ML)信道估计算法——DE-ML算法。仿真结果表明该算法在使用较少导频信息的情况下,通过差分进化方法有效估计跟踪有效信道长度,其估计性能优于最小二乘(LS)、线性最小均方误差(LMMSE)、传统ML等经典信道估计算法。该算法能在提高系统传输效率的同时显著提高算法的估计精度,尤其在高速移动情况下也具有了非常良好的性能。
信道估计, 时变信道, 差分进化, 有效信道长度, 最大似然(ML)估计
0 引 言
进行地铁隧道环境下的无线通信信道估计具有实际意义。在地下隧道这一限定空间中,无线电波的传播与地面有很大的不同[1]。一方面隧道内天线传播时,多径效应远远大于地面,所引起的频率选择性衰落对宽带信号的影响愈发明显,从而造成严重的码间串扰(intersymbol interference,ISI)。另一方面,列车的快速移动以及隧道内轨道沿线地面设备等散射物所引起的多普勒频谱扩展,造成列车与轨道沿线地面之间的无线通信信道快速变化,从而引起时间选择性衰落[2,3]。本文针对隧道中列车与轨旁设备之间无线通信中无线传输信息快速变化的特点,提出了一种采用元胞差分进化(differential evolution, DE)算法实时获得有效信道长度的新型最大似然(maximum likelihood, ML)信道估计方法(简称DE-ML算法),并通过仿真验证了该方法的优越性。
1 相关研究
正交频分复用(orthogonal frequency division multiple,OFDM)技术可以把宽带频率选择性信道划分成若干窄带平坦衰落信道,从而具有很强的抗无线信道多径衰落和抗脉冲干扰的能力。因此OFDM技术所具有的抗多径干扰、子载波分配灵活以及多址接入等优势,使其非常适合列车无线通信这一存在多径传播的非对称业务的通信需求。而信道估计是其中关键的一个环节。OFDM信道估计的方法主要有盲估计、半盲估计以及非盲估计三种[4]。其中盲估计和半盲估计的计算量大,对接收机的运算处理能力要求较高。而利用导频的非盲信道估计方式对频率选择性衰落较敏感,主要用于较快衰落的无线信道中。对于列车无线通信这样快速变化的无线信道来说,必须考虑列车快速移动所带来的多普勒频移对接收设计特别是信道估计所造成的影响,适合采用基于导频的信道估计方法。
近年来,基于导频的OFDM系统信道估计算法得到广泛的研究。其中,最优信道估计是采用最小均方误差(minimum mean square error, MMSE)准则[5],但遵循该准则的估计算法最大的缺点就是需要已知信道的统计特性,并且计算复杂度太高,因此对其进行低秩估计因为能够在获得较高性能的情况下明显降低复杂度而备受关注。Deneire[6]等提出一种低复杂度的最大似然(ML)信道估计算法,该算法在信道的频率相关特性位置未知的情况下,依据信道最大时延扩展和信噪比估计信道特性,但该算法对有效信道长度有一定的依赖性;文献[7]不需要预先知道信道最大时延扩展以及信噪比,利用平滑频域滤波器平滑相邻子载波处信道估计值,从而降低ML信道估计算法对有效信道长度的敏感度,但是作者并未给出确切的平滑次数,且该ML信道估计器复杂度较高;文献[8]提出利用线性搜索策略提供更加接近实际的有效信道长度,从而提高ML信道估计器的精度,但搜索机制过于单一,无法做到有效收敛。对于轨道无线信道这一快速时变信道而言,该搜索的算法过于复杂,不足以获得实时有效信道长度。针对高速移动用户,文献[9]提出了基于导频辅助的联合载波频偏与双选择性的信道估计算法,实现低复杂度的正交频分多址(orthogonal frequency division multiple access, OFDMA)迭代均衡方案。由于高速移动时信道为非静态,估计信道时信息量将会激增,因此传统估计方法很难实现完整信道的估计。本文针对上述估计难题,提出差分进化(DE)和最大似然(ML)估计相结合的时变信道估计方法,在获得实时的有效信道长度的基础上,利用ML信道估计算法获得整个信道特性,从而提高信道估计算法的性能。通过仿真比较,本文提出的信道估计算法的性能优于最小二乘(least square,LS)、线性最小均方误差(linear minimum mean square error, LMMSE)以及ML算法等经典信道估计算法。
2 OFDM系统模型
经典OFDM系统模型如图1所示。假定系统的子载波数为K,输入符号经过快速傅里叶反变换调制到相互正交的K个子载波上。为了克服OFDM符号间因信道的多径效应带来的码间串扰并保持OFDM符号间的正交性,需在前后符号间需保护间隔,并且其长度大于信道的最大时延τmax。通常OFDM系统中通过在保护间隔内加入循环前缀(cyclic prefix, CP),长度为MCP,从而实现保证子载波间的正交性。
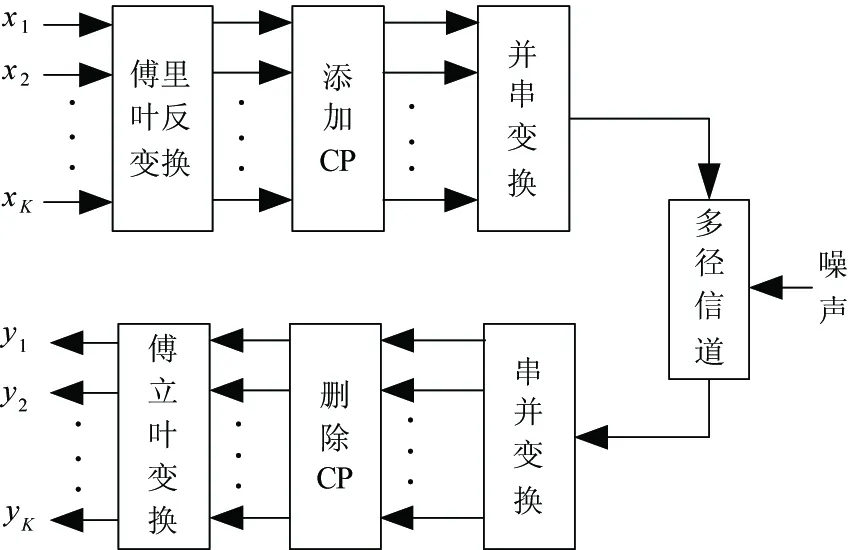
图1 OFDM系统模型
整个OFDM系统中发送模块与接收模块之间由多个路径的冲激信号组成一个衰落多径信道,其数字模型表示如下:
(1)
其中L为多径信道的路径数,αl为其中第l个路径增益,τl为第l个路径归一化时延;Ts为系统的采样周期。实际系统中,参数αl与τl都非常难估计,文献[10]提出了一种简化假设,即信道各径的功率延迟谱服从负指数分布:θ(τl)=Ce-τl/τrms。其中系数C为常数,均方时延扩展τrms为常数。整个系统可以用下面的表达式描述:
Y=XH+N
(2)
其中,X、Y分别为系统输入和输出向量;H=[h1,…,hk,…,hK]T为信道衰落因子向量,其中(·)T表示矩阵转置运算;N为独立同分布的加性高斯白噪声向量,其均值为零,方差为σ2,并且假设加性噪声N与信道特性H不相关。
3 OFDM最大似然估计算法
传输信道的冲激响应h是有限长的,而实际的有效长度Mh无法准确获得,通常的处理方法为取一个整数M作为假设的有效信道长度,M的取值范围是Mh≤M≤MCP。定义一个维数为M的列向量hM:
hM=[hT,0,…,0]T
(3)
该向量的前M个元素为hT,其余为0。
将式(3)代入系统特性公式(式(2))中,可得
Y=XFMhM+N
(4)

(5)
其中(·)H表示共轭矩阵运算,则可得信道冲击响应的传统ML信道估计量(时域)为
(6)
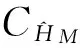
=Q/SNR
(7)

(8)
显然,ML估计量的均方误差依赖于假设的有效信道长度M的选择,与假设的有效长度的选取M成线性关系。
同时需要说明的是上述推导是在Mh≤M≤MCP条件下得出的。这是当M≤Mh时,由于假设的信道抽头个数比实际的还要少,这样无论如何也不可能完全恢复信道特性,此时估计量的归一化均方误差和M不再成线性关系,估计性能急剧恶化[8]。现定义归一化的均方误差如公式
(9)
用此公式来评估信道估计的性能。
因此,寻找恰当的有效信道长度M值就成为ML信道估计性能好坏的关键。下节将通过确定合适的适应度函数和优化算法寻找这一关键参数。
4 基于差分进化算法的最大似然信道估计算法
本节提出了元胞差分进化(cellular DE)算法[11]的最大似然信道估计算法,通过最小化的归一化均方误差寻找有效信道长度,从而获得最优的OFDM信道最大似然估计。下面给出差分进化算法进化个体、适应值函数以及控制参数的设置。
4.1 差分进化个体
本节中差分进化(DE)算法被用来寻找有效信道长度,因此式(9)中有效信道长度M被定义为差分进化的个体,其中维度D为1,个体定义如下式所示:
(10)
4.2 适应度函数
需找实时有效信道长度的目的是尽可能的降低ML信道估计的误差,归一化的均方误差用来评估信道估计的性能,该误差的定义见式(9)。因此差分进化算法的适应度函数定义为
(11)
差分进化算法的进化策略采用文献[11]提出的基于混沌局部搜索的元胞差分进化算法机制。考虑到整个优化问题的规模及维度D较小,参数设置如下:F初始值为0.5并在进化过程中自适应调整,交叉操作采取正交交叉策略,种群规模NP=5D,元胞邻居结构、进化规则以及混沌局部优化(chaotic local search,CLS)设置见文献[11],最大截止代数为50。基于元胞差分进化优化的最大似然信道估计算法具体步骤如下:
步骤1 设置差分进化算法的所有参数以及迭代的终止条件;初始化待估计OFDM传输系统模型等。
(1) 初始化NP=np×np个向量组成初始种群。
(2) 初始化元胞自动机由NP=np×np个向量组成的环形拓扑。
(3) 产生正交交叉表。
(4) 初始化CLS算子的参数。
步骤2 设置式(11)为差分进化算法的代价函数。
(1) 变异、交叉以及选择操作。
(2) 更新CLS算子的参数。
步骤3 对最优解进行CLS操作。
步骤4 依据元胞自动机的演化规则,更新各元胞状态;进化代数更新:g=g+1。
步骤5 终止条件满足,获得最小归一化信道估计归一化均方误差(NMSE);否则调至步骤2。
步骤6 获得有效信道长度M,采用ML信道估计准则得出导频位置信道的频率响应,输出最终结果。
步骤7 采用线性插值方法,获得非导频位置处信道信息,得出整个频域的信道信息。
5 仿真结果分析
为了验证估计算法的性能,本节对所提出基于元胞差分进化的ML信道估计算法(DE-ML算法)与其他经典信道估计算法进行了仿真比较。OFDM系统仿真的条件如表1所示,其中多普勒频移设定为0Hz、178Hz(分别对应地铁列车静止、时速80km/h两种状态);导频间隔为4(符合抽样定律)和8(违反抽样定律)。
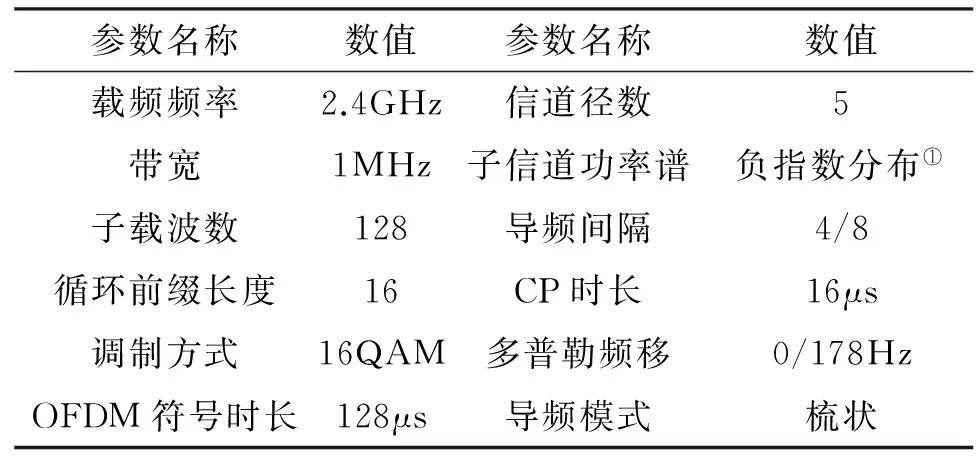
表1 仿真参数设置
注①负指数分布e-τl/τrms,τl为各径延迟,τrms=(1/4)cp时长
图2、图3分别给出了在导频间隔为4和8时的最小二乘(LS)算法、线性最小均方误差(LMMSE)算法、经典ML算法[6]及本文提出的新型DE-ML算法的误码率(BER)性能随信噪比(SNR)变化的曲线。从图中可以看出LS算法BER性能最差,LMMSE、ML算法BER性能次之;而本文提出的DE-ML算法的BER性能最优。
在导频间隔为4时,ML算法由于其他两种经典算法,但当导频间隔增加到8时,ML估计性能退化为与LMMSE算法基本相同。DE-ML算法在导频间隔为4,其BER性能略优于ML算法;但当导频间隔为8时,其性能明显优于ML算法,随着SNR增加其BER值下降速度更快。
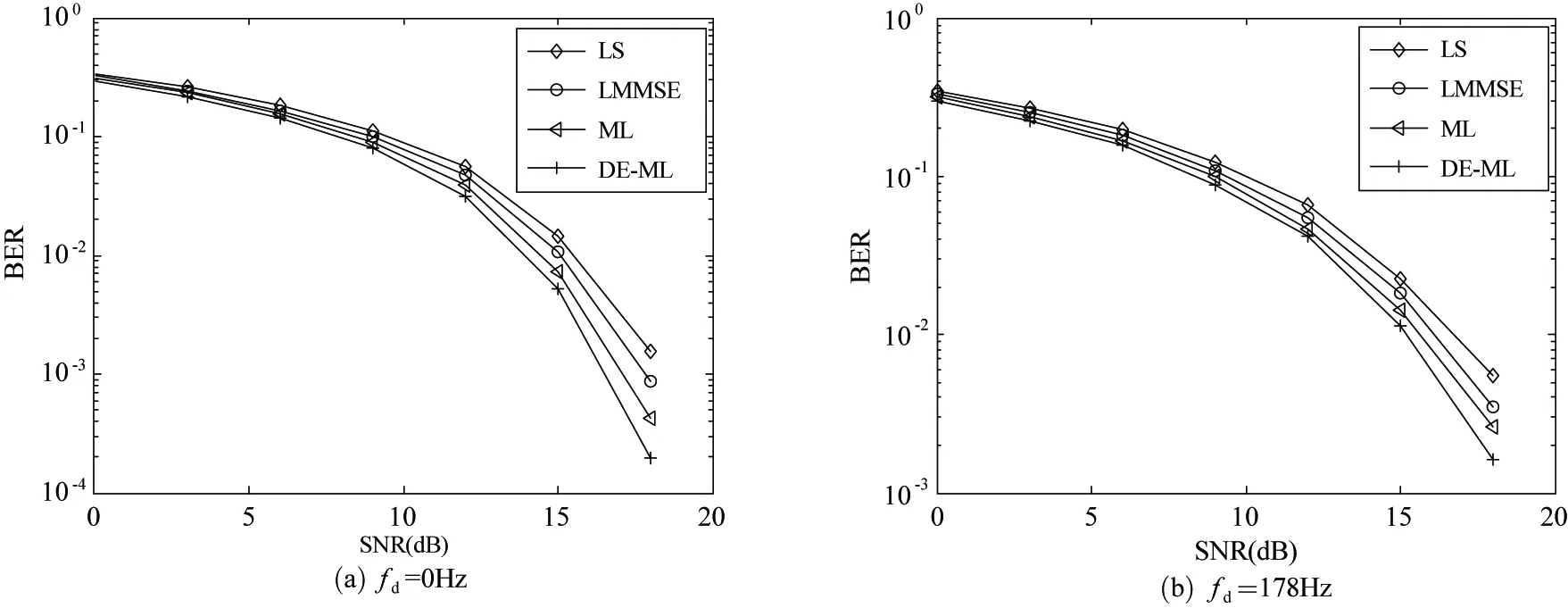
图2 LS、LMMSE、ML及DE-ML算法BER性能曲线(导频间隔为4)
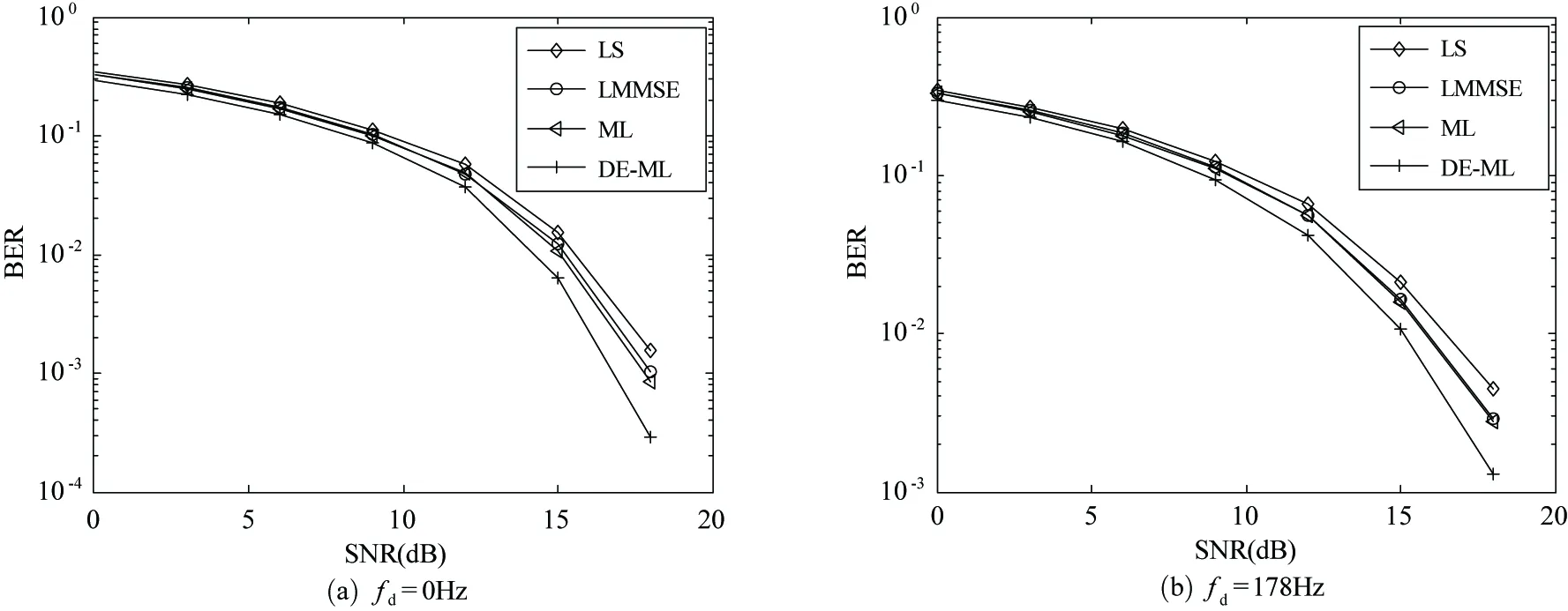
图3 LS、LMMSE、ML及DE-ML算法BER性能曲线(导频间隔为8)
6 结 论
通过利用元胞差分进化算法实时获取有效信道长度,采用归一化的信道冲击响应均方误差做为其优化目标,从而实现了一种基于元胞差分进化的最大似然信道估计算法。仿真结果表明:在违反采样定律的条件下,采用差分进化算法可实时获取有效信道长度,用较少导频信号获得优于典型最大似然算法的信道估计性能,从而提高了系统的传输效率;另外论文进一步研究了在列车处于静止、高速两种状态下列车与轨旁设备之间时变信道使用本文所提算法的估计性能,仿真结果表明,在导频间隔超出抽样定律所限制的距离时,本文所提出的基于元胞差分进化的最大似然估计算法估计性能明显优于其他经典算法。仿真结果验证了所提算法获得了估计精度与系统传输效率的较好平衡,具有很好的鲁棒性。此信道估计技术还可以与信号检测构成联合迭代接收技术,从而进一步提高无线通信接收机性能。
[1] Karimi O B, Liu J and Wang C. Seamless wireless connectivity for multimedia services in high speed trains.IEEEJournalonSelectedareasincommunications, 2012, 30(4): 729-739
[2] Ferrer-Coll J, Ngskog P A, Chilo J, et al. Characterization of electromagnetic properties in iron-mine production tunnels.ElectronicsLetters, 2012, 48(2):62-63
[3] Wang Y, Kong B, Leung H, et al. An experimental vehicular wireless system and link performance analysis.IEEE/ASMETransactionsonMechatronics, 2012, 17(3):508-518
[4] Fang X, Xu Y, Chen Z, et al. Frequency-domain channel estimation for polarization-division-multiplexed CO-OFDM /OQAM systems.JournalofLightwaveTechnology, 2015, 33(13):2743-2750
[5] Takano Y, Juntti M, Matsumoto T. l1 LS and l2 MMSE-based hybrid channel estimation for intermittent wireless connections.IEEETransactionsonWirelessCommunications, 2016, 15(1):314-328
[6] Deneire L, Vandenameele P, Vander P L, et al. A low-complexity ML channel estimator for OFDM.IEEETransactionsonCommunications, 2003, 51(2):135-140
[7] Wang Z J, Mathew G, Yan X, et al. A robust maximum likelihood channel estimator for OFDM systems. In: Proceedings of the Wireless Communications and Networking Conference (WCNC 2007), Hong Kong, China, 2007. 169-174
[8] 张建康,陈恩庆,穆晓敏等. OFDM系统中一种最大似然信道估计算法. 兵工学报, 2009, 30(9):1206-1210
[9] Muneer P, Sameer S M. Joint ML estimation of CFO and channel, and a low complexity turbo equalization technique for high mobility OFDMA uplinks.IEEETransactionsonWirelessCommunications, 2015, 14(7):3642- 3654
[10] 3GPP TR25.814, V7.1.0. Physical layer aspects for evolved universal terrestrial radio access (UTRA) (Release 7). Valbonne: EGPP, 2006-09
[11] 丁青锋,郑国莘,杨柳. 基于反学习和正交交叉算子的元胞差分进化算法. 北京邮电大学学报, 2014,37(3):7-12
An algorithm for maximum-likelihood estimation of time-varying channels based on differential evolution
Ding Qingfeng, Qiu Xiang
(School of Electrical and Automation Engineering, East China Jiaotong University, Nanchang 330013)
The estimation of the communication channels in tunnel environment was studied, and a new maximum-likelihood (ML) channel estimation algorithm using the cellular differential evolution (DE) algorithm to achieve the real-time estimation of the effective length of time-varying channels was designed to deal with the rapid changing wireless transmission channels under the tunnel environment. The algorithm is simplified as the DE-ML algorithm. The simulation results show that the proposed algorithm can effectively track the effective channel length to improve the estimation accuracy by the differential evolution algorithm. And its estimation performance outperforms the classic channel estimation algorithms such as least square (LS), linear minimum mean square error (LMMSE) and traditional ML, etc. The proposed algorithm can offer high transmission efficiency and excellent estimation performance especially at time-varying channels.
channel estimation, time-varying channel, differential evolution, length of effective channel, maximum-likelihood (ML) estimation
10.3772/j.issn.1002-0470.2016.06.002
①国家自然科学基金(61501186,51267005)和江西省教育厅科学基金(GJJ150491)资助项目。
2016-03-07)
②男,1980年生,博士,副教授;研究方向:轨道交通无线通信,进化算法等;联系人,E-mail: brandy724@sina.com

