Identity-based proxy multi-signature applicable to secure E-transaction delegations①
Liu Jianhua (刘建华), Wu Qianhong, Liu Jianwei, Shang Tao
(*Aviation Engineering Institute, Civil Aviation Flight University of China, Guanghan 618307, P.R.China) (**School of Electronics and Information Engineering, Beihang University, Beijing 100191, P.R.China)
Identity-based proxy multi-signature applicable to secure E-transaction delegations①
Liu Jianhua (刘建华)②*, Wu Qianhong**, Liu Jianwei**, Shang Tao**
(*Aviation Engineering Institute, Civil Aviation Flight University of China, Guanghan 618307, P.R.China) (**School of Electronics and Information Engineering, Beihang University, Beijing 100191, P.R.China)
To enhance the robustness of a proxy multi-signature scheme and improve its efficiency, a novel proxy signature paradigm is proposed referred to as identity-based proxy multi-signature (IBPMS). In this paradigm, multiple proxy signer candidates are employed to play a role of the single proxy signer in the existing model. A provably secure IBPMS scheme is presented which requires only one round broadcast operation. Performance analysis demonstrates that the new scheme outperforms the existing multi-signature schemes in robustness and communication. These properties are rendered to our IBPMS scheme as a more practical solution to secure e-transaction delegation applications of proxy signatures.
multi-signature, E-transaction, delegation, provable security, information security
0 Introduction
Digital signature protocols allow message transmissions among a group of users with non-repudiation, user identification, and message authentication. Many variants of signatures such as blind signature[1], proxy signature[2], multi-proxy signature[3], and proxy multi-signature (PMS for short)[4]have been proposed to meet different application demands, among which, the proxy signature protocol is constructed to empower a signee to issue a message on behalf of another signee.
Proxy multi-signature plays an critical role in the following scenarios. There may be real estate owned bym(m>1) entities, any legal transaction that wants to sell or rent out the assets must be permitted by all themowners. In other words, it must be signed jointly by all the entities, or signed by their designated proxy signers. For the latter case, any transaction of the real estate needs to be executed with the permission issued by all the owners’ proxy signers. One practical solution to the problem is to allow multiple proxy signers in a proxy multi-signature, each owner has his/her own proxy signer.
The PMS scheme[5]needs only one round broadcast operation for each original signer during the proxy key generation phase. The proxy multi-signature schemes in Refs[4-6] do not provide formal definition or security model. Cao et al. proposed an ID-based proxy multi-signature scheme which used bilinear pairings[7].
The existing PMS schemes (e.g., Ref.[5-9]) only allow one proxy signer candidate. This limitation may incur a bottleneck to the PMS schemes in some applications. Multi-proxy multi-signature[10,11]allow multiple original signer to delegate their signing capability to a group of proxy signers. Consider a scenario where a real estate owned by multiple owners needs to be rent out or sold. Suppose the owners delegate their signing capability to some proxy signers. If there is only one single proxy signer allowed to sign on behalf of the owners, then the single proxy signer’s relationships with the owners are different from each other. He/She may issue some transaction documents which will meet some owners’ interests but damage the interests of other owners. To address the drawback, a plausible solution is to allow the owners to choose their own proxy signers, any owner can designate a proxy signer. A transaction document is legal if and only if all the proxy signers sign on it. Another issue in existing PMS schemes is their communication complexity. Each original signer needs two-round broadcast operations. It’s critical to reduce the number of interaction rounds.
Contribution of the study: Motivated by the above observations and the work of Ref.[12], this work revisits proxy multi-signatures. The contribution consists of two folds. First, a general framework to identity-based proxy multi-signature (IBPMS) is presented. In IBPMS, the original signers of a group are allowed to transfer their signing rights to a group of proxy signer candidates and any proxy signer candidate can sign a document on behalf of all the original signers alone. Second, an IBPMS scheme is proposed which is provably secure under standard computational assumptions. A striking feature of the IBPMS scheme is that it demands only one time of broadcasting operation for each original signer during the proxy key generation phase.
The rest of this paper is organized as follows. Some background knowledge associated with the work is given in Section 1. The outline of the proxy multi-signature scheme and security model are given in Section 2. In Section 3, a proxy multi- signature scheme from bilinear pairing is presented. Its formal security proofs will be given in Section 4. In Section 5, the efficiency of the proposed scheme is compared with some related work. conclusion is given in Section 6.
1 Syntax
In the conventional proxy signature definition, a proxy signer can sign a message on behalf of an original signer under the delegation of the original signer. In Ref.[13], Huang, et al. proposed a security model of a proxy signature scheme. This model is the most widespread used one for the security analysis. A delegation usually is produced by the original signer through an algorithm whose inputs are private key and a certain message. Therefore, a delegation can be seen as a special signature signed by the original signer(In most cases, it is a signature on a warrant).
Usually, there is only a single proxy signer in a PMS scheme[5-8]. All the original signers delegate their signing capability to one proxy signer. If the designated proxy signer is unavailable for something unexpected, then the protocol will be collapsed. Therefore, the proxy signer may be a bottleneck of a PMS scheme. One efficient solution to reduce the bottleneck effect is to increase the number of proxy signers and each proxy signer can sign a message on behalf of all the original signers separately.
1.1 Protocol variables and member relationship

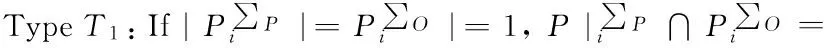
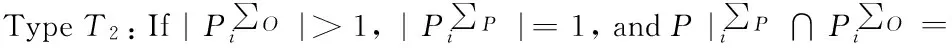
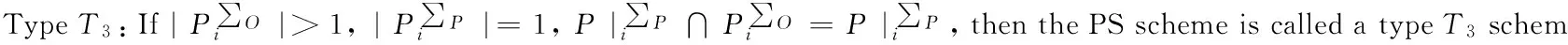
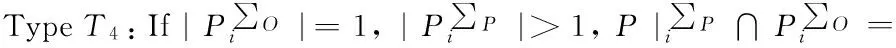
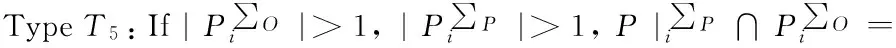

Traditional proxy multi-signature[7]is a type T2scheme, a traditional multi-proxy signature scheme[3]is a type T4scheme, a (t,n) threshold proxy signature schemes[14]is a type T4scheme.
1.2 Bilinear parings

The bilinear map can be constructed by suitable modification in Weil[15]or Tate pairings[16]. The group equipped with such a map is called a bilinear group, on which the Decisional Diffie-Hellman problem is able to be solved within a polynomial-time while the computational Diffie-Hellman problem is believed hard[17].
2 Modelling identity-based proxy multi-signature
Inspired by the works of Cao, et al.[7], Wang, et al.[18], and Rajeev, et al.[8], and Pointcheval[19], a formal definition and security model for identity-based proxy multi-signature schemes are given.
2.1 Definition of identity-based proxy multi-signature schemes
In an identity-based proxy multi-signature scheme, the original signers of a group are allowed to transfer their signing rights to a group of proxy signer candidates, in such a way that any proxy signer candidate can sign a document on behalf of all the original signers alone. LetA1,A2,…,Ambe the original signers andB1,B2,…,Bnbe the proxy signer candidates designated byA1,A2,…,Am. For 1≤i≤m, Aihas an identity IDAi, for 1≤j≤n,Bjhas an identity IDBj.
Definition 1 An identity-based proxy multi-signature scheme is a tuple IBPMS=(Setup; Extract; Sign; Veri; PMGen; PMSign; PMVeriT).
Setup: On the input security parameterl, PKG generates public parametersParaof the system and a master secret keys. PKG publishesParaand keeps confidential master keys.
Extract: Input master secret keys, public parametersParaand an identityID, and output the private keySIDofID. PKG will use this algorithm to generate private keys for all entities participating in the scheme and send the private keys to their respective owners through a secure channel.


PMGen: This is a protocol jointly executed by all the candidate proxy signers and all original signers. Input IDA1,…,IDAm,IDB1,…,IDBn, the original signers’ private keys SIDA1,…,SIDAmand the delegation warrant ω which includes the type of the information delegated, the period of delegation, all the candidate proxy signers, etc. Any candidate proxy signerBj(j=1,…,n) can output a proxy signing key skBjby inputting his secret key SIDBj. The proxy signing key skBjcan be used byBjto produce proxy multi-signature on behalf of the original signers.

2.2 Security model
A formal security model for an identity-based proxy multi-signature scheme based on the work of Refs[7,8,20] is given. It is considered that adversary A tries to forge a proxy multi-signature working against a single honest user 1. User 1 can be an original signer or a proxy signer adaptively. A is allowed to access standard signing oracle, delegation oracle, and proxy multi-signature oracle.
The goal of adversary A is to produce one of the following forgeries:



Consider the following game:
(1) Setup: The challenger runs the algorithm Setup of the proxy multi-signature scheme and provides the public parametersParato A.
(2) Hash query: A can access the hash oracle, challenger X responds through the hash oracle and maintains LH1, LH2and LH3for each hash query.
(3) Extract query: Adversary A can ask for the private key of any user IDi(IDi≠ID1). The challenger responds by running the Extract algorithm and returns the private key SIDito A.

(5) Delegation query: A is allowed to request for the proxy signing key on the warrant ω and the identity IDi(IDi≠ID1). The user 1 may be either one of the original signers or one of the proxy signers.

Definition 2 ID-based proxy multi-signature forger A (t,qH,qE,qs,qps,qpms,m+n,ε)-breaks them+nusers ID-based proxy multi-signature scheme by the adaptive chosen message and givenIDattack if: A runs in time at mostt, and A makes at mostqHqueries to the hash queries, at mostqEqueries to the extraction queries, at mostqsqueries to the signing queries, at mostqpsqueries to the delegation queries and at mostqpmsqueries to the proxy multi-signature queries, and the success probability of A is ε at least.
Definition 3 An ID-based proxy multi-signature scheme is (t,qH,qE,qs,qps,qpms,m+n,ε)-secure against adaptive chosen message and givenIDattack, if there is no adversary who can (t,qH,qE,qs,qps,qpms,m+n,ε)-break it.
3 Proposed identity-based proxy multi- signature scheme
In this section, an identity-based proxy multi-signature (IBPMS for short) scheme is presented based on the ID-based aggregate signature scheme[12]and IBPMS scheme[8]. The scheme has following phases: Setup, Extract, Sign, Veri, PMGen, PMSign, PMVeri.
Extract: For a user withID, PKG computes its public key as QID=H1(ID)∈G1and private key asSID=sQID. Thus original signerAi, has its public key QAi(for i=1,…,m) and corresponding private key SIDAi. Similarly, for thenproxy signers, the public keys are QIDBjand corresponding private keys are SIDBj(forj=1,…,n).

The Sign and Veri algorithm above is the same algorithm as the Shim’s IBS scheme[12], and for short the Shim’s IBS scheme is denoted as SIBS.
PMGen: In this phase, the original signers perform the following job to make a message warrant ω, jointly with the proxy signers. ω includes some specific information about the message, restrictions on the message, time of delegation, identity of original and proxy signers, period of validity, and so on. Unlike the traditional proxy multi-signature schemes, the warrant ω in our scheme will declare a proxy signer group {Bj|1≤j≤n}, any Bjcan sign a message on the behalf of the original signers {Ai|1≤i≤m}.
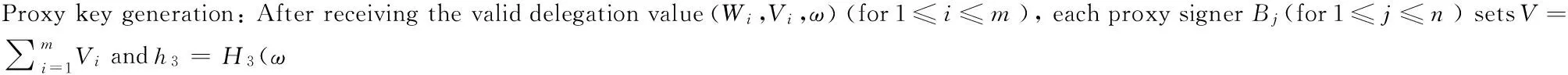
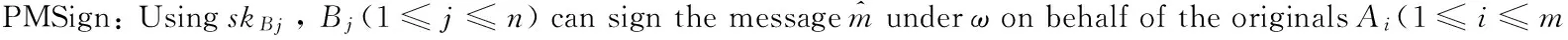

WBj=skBj+xjh4Ppub



2. Checks whether or not the proxy signerBjis on the authorized list in the warrant ω. If not, stop. Otherwise, continue.

Our PMS scheme allowsncandidates of proxy signingB1,…,Bn. Ifn=1, then our PMS scheme is a traditional PMS scheme, namely a T2proxy signature scheme; Ifn>1, then the PMS scheme is a T5proxy signature scheme.
If set the number of proxy signersn>1 in the PMS scheme, and use the PMS scheme to be a traditional PMS scheme, that is to say, a message can be checked as valid when one of the proxy signers signs on it. In this situation, the proposed PMS scheme enjoys better robustness than a traditional PMS scheme, because, a traditional PMS scheme will not work if the unique proxy signer is not available. Thus a T5scheme enjoys better robustness than a T2scheme if a message needs only one proxy signer to sign on it.
An e-transaction application instance: Suppose there is a real estate owned by multiple entities needed to be sold out. The owners authorize proxy signers to sign e-transaction documents. If there is only one single proxy signer allowed to sign messages on behalf of all the owners, then how to choose the single proxy signer admitted by all owners is another open problem. The relationship between the single proxy signer and ownerAiis different from that between the single proxy signer and owner Aj(i≠j). By using the proposed PMS scheme, each owner is allowed to choose her/his own proxy signer, thenmoriginal signers havenproxy signers, therem=n. Any e-transaction document can be verified as valid only if all thenproxy signers sign on it. The whole process containsmtimes PMSign signing andmtimes PMVeri verifying.
4 Analysis of the scheme
4.1 Correctness
1. The correctness of delegation process:

2. The correctness of PMSign and PMVeri algorithms from the following equalities:


4.2 Security proof
ε≥e(qE+1)·(1+(1-1/(qE+1))qpms)
+(1-1/(qE+1))qs+qps+qpms)-1ε’
t≤t’-CG1(qH1+qH2+qH3+qH4+2qE
+3qs+3qps+3qpms+9)
whereeis the base of natural logarithms, and CG1is the time of computing a scalar multiplication and inversion onG1.
Proof. Suppose adversary (t,qH,qE,qs,qps,qpms,m+n,ε)-breaks the proxy multi-signature scheme. X is given X=xP and Y=yP. Its goal is to output xY=xyP. X interacts with A as follows:
Setup: Algorithm X initializes A withPpub=Xas a system’s master public key. A selects an identityID1.
H1-queries: At any time A can query the random oracle OH1. To respond to these queries, X maintains a list LH1of tuples (IDi,Qi,bi,ci) . When an identityIDiis submitted to the OH1, X responds as follows:
(1) If the queryIDialready appears on the list LH1in some tuple (IDi,Qi,bi,ci), then algorithm X responds withH1(IDi)=Qi.
(2) Otherwise, X generates a random coin c∈{0,1} such that Pr[c=0]=λ.

(4) Algorithm X adds the tuple (IDi,Qi,bi,ci) to the list LH1and responds to A withH1(IDi)=Qi.
H2-queries: A can query the random oracle OH2. X maintains a list LH2of tuples (ωi,vi). When a warrant ωiis submitted to the OH2, X responds as follows:
(1) If the query ωialready appears on the list LH2in some tuple (ωi,vi) then algorithm X responds with H2(ωi)=vi.
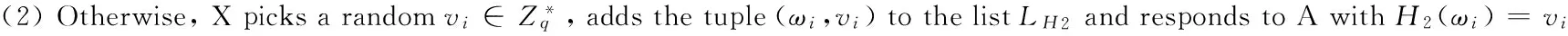
H3-queries: At any time A can query the random oracle OH3with (ω,V). X maintains a list LH3of tuples (ω,V,η). X responds as follows:

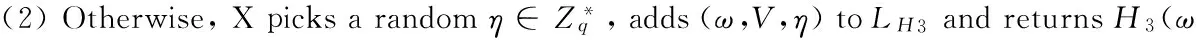

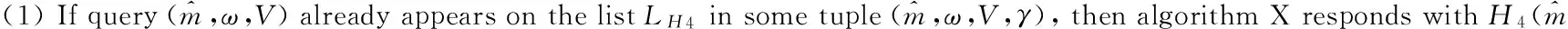

Extraction queries: Let IDi(i≠1) be a private key extraction query issued by algorithm A.
(1) X runs the above algorithm for responding toH1-queries to obtain a Qi∈G1such that H1(IDi)=Qi. Let (IDi,Qi,bi,ci) be the corresponding tuple on the list LH1. Ifci=0, then X outputs “failure” and terminates.
(2) Otherwiseci=1 and Qi=biP. Define SIDi=biPpub. It is seen that SIDi=bixP=xQiand therefore SIDiis the private key associated with the public keyIDi. Returns SIDi. The probability of success is 1-λ.


Delegation queries:

Case 2: A requests to interact withID1, whereID1plays the role of one of the original signers. To responds to this query, A generates a warrant ω, and requestsID1to sign ω and receives a response (WA1,VA1,ω). X returns a partial proxy signing key skBjwhich involves (WA1,VA1,ω) and adds ((WA1,VA1),…,(WAm,VAm),ω,skBj) to Lpso.

Hence the above provided proxy signing key which involves (WAi,VAi) is valid. The probability of success is 1-λ.


(2) X runs the above algorithm for responding toH2-queries on ω, recovers (ω,v) on LH2list.
(3) Ifc= 0, then X returns “failure” and terminates. Ifc=1, H1(IDAi)=bAiP or H1(IDBj)=bBjP.

Hence, the probability thatCdoes not abort during the simulation is (1-λ)qE+qps+qpms.
Output: If X does not terminate as a result of A’s extraction query and proxy multi-signature query, then A’s view is identical to its view in the real attack.
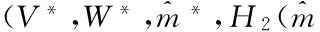
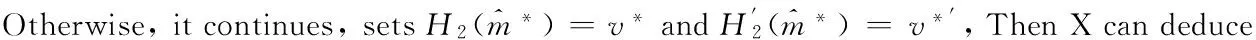
And it holds that
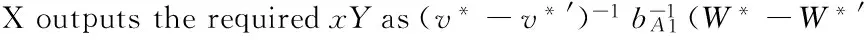
X succeeds if all of these events happen.
Pr[E1∧E2∧E3]
=Pr[E1]Pr[E2|E1]Pr[E3|E1∧E2].
Since A makes at mostqEqueries to the Extraction oracle and Pr[c=1]=1-λ, then Pr[E1]=λ(1-λ)qE. If X does not abort as a result of A ’s Extraction query then A ’s view is identical to its view in the real attack. Hence, Pr[E2|E1]≥ε. X will abort only if A generates a forgery such thatc=1. Hence, Pr[E3|E1∧E2]≥1/(1-λ). Thus, the probability of success is at least λ(1-λ)qEε.



Hence the success probability that X solves the CDHP in the above game is at least:
((1-λ)qE+(1-λ)qE+qpms+(1-λ)qE+qs+qps+qpms)λε Set λ=1/(qE+1), we can deduce that
((1-1/(qE+1))qE+(1-1/(qE+1))qE+qpms+(1-1/(qE+1))qE+qs+qps+qpms)1/(qE+1)ε≥(1/e)·1/(qE+1)·(1+(1-1/(qE+1))qpms+(1-1/(qE+1))qE+qs+qps+qpms)ε≥ε′.
Therefore
ε≥e(qE+1)·(1+(1-1/(qE+1))qpms
+(1-1/(qE+1))qE+qs+qps+qpms)-1ε′
For the running time, one can observe that the running time of X is the same as A running time plus the time taken to respond to qH1,qH2,qH3,qH4hash queries,qEextraction queries,qssigning queries,qpsdelegation queries andqpmsproxy multi-signature queries, and the time to transform A ’s final forgery into the CDH solution. Hence, the total running time is at most t+CG1(qH1+qH2+qH3+qH4+2qE+3qs+3qps+3qpms+9)≤t′ as required.
5 Comparison
The efficiency of the scheme is compared with the schemes in Refs[6-8]. In Table 1,Edenotes the exponentiation operation inG2,Mdenotes the point scalar multiplication operation inG1,Pdenotes the pairing operation and NoPS denotes the number of proxy signer candidates. The broadcasting round in which each original signer needs to execute in the PMGen is denoted by BREO.

Table 1 Performance analysis
From Table 1, it can be seen that the proposed scheme is more efficient than the schemes in Refs[6-8]. Especially, the PMS scheme demands only one round broadcasting operation for each original signer, and the proxy signer candidates is not unique. These two characteristics make our PMS scheme more practical and efficient than the other schemes. It is supposed a valid message only needs the signature of one of the proxy signers.
6 Conclusion
In this work, a novel proxy multi-signature scheme is presented. The proposed proxy multi-signature scheme demands only one round broadcasting operation for each original signer during the proxy key generation phase. The scheme allows multiple proxy signers, improves the reliability of the PMS scheme. A formal security proof for the proposed scheme is also proposed.
[1] Boldyreva A. Threshold signatures, multisignatures and blind signatures based on the Gap-Diffie-Hellman-group signature scheme. In: Proceeding of the Public Key Cryptography, Miami, USA, 2003. 31-46
[2] Mambo M, Usuda K, Okamoto E. Proxy signature: delegation of the power to sign messages.IEICETransactionsonFundamentalsofElectronicsCommunications&ComputerSciences, 1996, E79-A(9):1338-1353
[3] Cao F, Cao Z F. A secure identity-based multi-proxy signature scheme.ComputersandElectricalEngineering,2009, 35:86-95
[4] Yi L, Bai G, Xiao G. Proxy multi-signature scheme: a new type of proxy signature scheme.ElectronicsLetters, 2000, (36):527-528
[5] Li X X, Chen K F, Li S Q. Multi-proxy signature and proxy multi-signature schemes from bilinear pairings. In: Proceedings of the 5th International Conference on Parallel and Distributed Computing, Application and Technologies, Singapore, 2004, 2004.591-595
[6] Li X X, Chen K F. ID-based multi-proxy signature, proxy multi-signature and multi-proxy multi-signature schemes from bilinear pairings.AppliedMathematicsandComputation, 2005,169(1):437-450
[7] Cao F, Cao Z. A secure identity-based proxy multi-signature scheme.InformationSciences, 2009, 179(3):292-302
[8] Rajeev A S, Sahadeo P. Efficient ID-based proxy multisignature scheme secure in random oracle.FrontiersofComputerScience, 2012, 6(4):421-428
[9] Du H, Wen Q. Certificateless proxy multi-signature.InformationSciences, 2014, 276:21-30
[10] Asaar M R, Salmasizadeh M, Susilo W. An identity-based multi-proxy multi-signature scheme without bilinear pairings and its variants.ComputerJournal, 2013,58(4):1021-1039
[11] Sahu R A, Padhye S. Identity-based multi-proxy multisignature scheme provably secure in random oracle model.TransactionsonEmergingTelecommunicationsTechnologies, 2015,26(4):547-558
[12] Shim K. An ID-based aggregate signature scheme with constant pairing computations.TheJournalofSystemsandSoft-ware, 2010, 83:1873-1880
[13] Huang X Y, Mu Y, Willey S, et al. Proxy signature without random oracles. In: Proceedings of the Mobile ad-hoc and Sensor Networks, Hong Kong, China, 2006. 473-484
[14] Zhang K. Threshold proxy signature schemes.LectureNotesinComputerScience, 1997, 1396: 191-197
[15] Boneh D, Franklin M. Identity-based encryption from the weil pairing. In: Proceedings of the Crypto, Santa Barbara, USA, 2001. 213-229
[16] Miyaji A, Nakabayashi M, Takano S. New explicit conditions of elliptic curve traces for fr-reduction.IEICETransactionsonFundamentals, 2001, 5:1234-1243
[17] Okamoto T, Pointcheval D. The gap-problems: a new class of problems for the security of cryptographic schemes. In: Proceedings of the Public key Cryptopraphy, Cheju Island, Korea, 2001. 104-118
[18] Wang Q, Cao Z, Wang S. Formalized security model of multiproxy signature schemes. In: Proceedings of the 5th International Conference on Computer and Information Technology, Shanghai, China, 2005. 668-672
[19] Pointcheval D, Stern J. Security arguments for digital signatures and blind signatures.JournalofCryptology, 2000, 13:361-396
[20] Shao Z. Improvement of identity-based proxy multi-signature scheme.JournalofSystemsandSoftware, 2009, 85:794-800
Liu Jianhua, born in 1983. He received his Ph.D degrees in School of Electronic and Information Engineering of Beihang University in 2013. He also received his B.S. and M.S. degrees from China West Normal University in 2006 and 2009 respectively. His research interests include information security.
10.3772/j.issn.1006-6748.2016.02.012
①Supported by the National Basic Research Program of China (No. 2012CB315905), the National Natural Science Foundation of China (No. 61272501), the Fund of Tianjin Key Laboratory of Civil Aircraft Airworthiness and Maintenance in CAUC and a General grant from Civil Aviation Flight University of China (No. J2013-31, Q2014-48).
②To whom correspondence should be addressed. E-mail: ljh2583265@163.comReceived on Aug. 22, 2015
 High Technology Letters2016年2期
High Technology Letters2016年2期
- High Technology Letters的其它文章
- An optimizing algorithm of static task scheduling problem based on hybrid genetic algorithm①
- Quotient space model based on algebraic structure①
- Learning trendiness from twitter to web: a comparative analysis of microblog and web trending topics①
- Distributed cubature Kalman filter based on observation bootstrap sampling①
- Intelligent outdoor video advertisement recommendation system based on analysis of audiences’ characteristics①
- Abnormal activity detection for surveillance video synopsis①
