An optimizing algorithm of static task scheduling problem based on hybrid genetic algorithm①

Liu Yu (柳 玉), Song Jian, Wen Jiayan

(The Scientific Research Department, Naval Marine Academy, Guangzhou 510430, P.R.China)



An optimizing algorithm of static task scheduling problem based on hybrid genetic algorithm①

Liu Yu (柳 玉)②, Song Jian, Wen Jiayan

(The Scientific Research Department, Naval Marine Academy, Guangzhou 510430, P.R.China)

To reduce resources consumption of parallel computation system, a static task scheduling optimization method based on hybrid genetic algorithm is proposed and validated, which can shorten the scheduling length of parallel tasks with precedence constraints. Firstly, the global optimal model and constraints are created to demonstrate the static task scheduling problem in heterogeneous distributed computing systems(HeDCSs). Secondly, the genetic population is coded with matrix and used to search the total available time span of the processors, and then the simulated annealing algorithm is introduced to improve the convergence speed and overcome the problem of easily falling into local minimum point, which exists in the traditional genetic algorithm. Finally, compared to other existed scheduling algorithms such as dynamic level scheduling(DLS), heterogeneous earliest finish time(HEFT), and longest dynamic critical path(LDCP), the proposed approach does not merely decrease tasks schedule length, but also achieves the maximal resource utilization of parallel computation system by extensive experiments.

genetic algorithm, simulated annealing algorithm, parallel computation, directed acyclic graph

0 Introduction

A parallel application can be abstracted as tasks sets, in which the elements are organized as a partial order and is in serial or parallel working mode. The task scheduling system allocates tasks to specified computers or processors and implement in parallel, based on some rules and constraints. In general, task scheduling algorithms are classified into two classes: static and dynamic, the former outputs scheduling schems in a compiling state, while the latter is made at run time. Static scheduling algorithms are widely used for their simplicity, high execution efficiency and low cost[1]. The task scheduling is to find a kind of tasks assignment scheme which can make application finished in the shortest time, and has been approved as an NP-complete problem. The results of scheduling decisions directly affect the total performance of distributed computing environment, even possibly offset the gains from distributed platform in worse case. Therefore, the design and implementation of an excellent task scheduling algorithm need to be focused and researched by computer scientists.

There are several static tasks scheduling algorithms: graphs[2], queuing theory[3], math programming[4]and heuristics, etc., where the last is the most popular. According to the characteristics of task retained, there are two types of heuristic algorithms: task duplication and non-task duplication, and it has been proved that the former is better than the latter[5], typical examples including TDS[6]and OSA[7]algorithms. For example, The TDS assign the nodes with their pre-order nodes at the same processor to decrease parallel executing time. As an improved version of TDS, the OSA achieves similar results by removing some unnecessary constraints. In summary, the mathematical models for previous static tasks scheduling algorithms belong to the integer-programming applications essentially. Although the heuristic and branching-bounding algorithms were introduced later to improve the algorithms speed and efficiency in some extent, their computing time remains unbearable, especially when facing many more tasks and processors, and their results are easy to produce early maturity and fall into local extreme points. Therefore it is difficult to take full advantage of high performance computing environment.

Genetic algorithm is a kind of highly parallel, randomized, adaptive search algorithm by learning nature selection and evolution mechanism from nature, which has excellent robustness and is especially suitable for complicated, non-linear problems puzzled by the traditional searching algorithm[8]. In this paper, by adding constraints such as heterogeneity, idle time interval and so on, an optimization model of static task scheduling is proposed in the heterogeneous distributed computing systems. In this model, by us real matrix coding seeds, combined with the simulated annealing in the process of evolution, the genetic population can achieve rapid convergence. As a result, the mixed integer nonlinear static task scheduling problems with multiple variables and constraints can be successfully solved and achieve to their global optimal solutions. Finally, results and performance of the proposed algorithm are tested by specific computational experiments and compared with other widely used scheduling algorithms.

The remainder of this paper is organized as follows: in Section 1, the research problem and some necessary assumptions are defined. Section 2 introduces the optimized mathematical model of task scheduling problem. Section 3 considerably depicts hybrid genetic algorithm. Section 4 conducts two sets of experiments to acquire the performance of the algorithm. Finally a conclusion and an overview of future work are given in Section 5.

1 Problem definition

Definition 1 The heterogeneous distributed computing system (HeDCSs) is a computing environment with heterogeneous computing nodes or heterogeneous interconnection network in which computational nodes are located in different geographical districts[9].

Hypothesis 1 Not considering the data transfer type, style, interface and other compiler details, a parallel application, can be represented by a directed acyclic graph (DAG). DAG is defined by the tuple (T,E), whereT={t0,t1,…,tN-1} is a set ofNtasks andE={eij=(ti,tj)|ti,tj∈T,i≠j} is a set of edges. Each edgeeijrepresents a precedence constraint and a communication message between taskstiandtj. That means ifeij∈E, then the execution oftjcannot be started beforetifinishes its execution. A task with no parents is called an entry task, and a task with no children is called an exit task. Associated with each edgeeij, there is a valuewijthat represents the amount of data to be transmitted from tasktito tasktj.

Hypothesis 2 Representing heterogeneity only through the difference of computing resources of processors which are fully connected. LetP={p0,p1,…,pM-1} denote a set of processors in the HeDCSs environment,Mis the number of processors, computing ability of tasks is described by two-dimensional matrixC=[cimorc(ti,pm)]N×M, wherecimdenotes the tasktiexecution time needed in the processorpmto reflect heterogeneity of computation.

Hypothesis 3 The calculating cost is monotonic, if ∃ti∈T,∃m, k∈{0,1,…,M-1} and m≠k,cim≥cik, then ∀tj∈T, cjm≥cjk.

Hypothesis 4 If the network data transmission rate is fixed, and the communication overhead of tasks executed in the same processors is zero, the communication cost between the two tasks can be measured by their interactive data amount.

To sum up, static task scheduling problem in heterogeneous distributed computing environment may achieve the following optimization goal:

① The time to complete all the parallel tasks is shortest;

② Communication overhead between parallel tasks is most economical;

③ Average waiting time of tasks is the shortest;

④ Balance processors allocation as far as possible

⑤ Improve the operation efficiency of the computing system as far as possible.

2 Problem modeling

If static tasks scheduling problemZcan be seen as two procedures: processors allocation and computing task executing time in the processor, it establishes its mathematical model through analyzing time relationship between the first executed task and the last one:

Z=min(F(tiN-1, PA(tiN-1))-S(ti0, PA(ti0)))

ti0, ti1,…, tiN-1∈T (1)

The constraint conditions:

(1) if ∀i, j∈{0,1,…,N-1}, ∃eij∈E， then F(ti, PA(ti))≥S(tj, PA(tj)).

(2) if ∀i, j∈{0,1,…,N-1}, ∃m∈{0,1,…,M-1} PA(ti)=PA(tj)=m， theneij=0.

(3) F(tiβ, PA(tiβ))=S(tiβ, PA(tiβ))+c(tiβ, PA(tiβ)), β∈{0,1,…,N-1}.

(4) if ∀Pm∈P,∀i, j∈{0,1,…,N-1}, PA(ti)=PA(tj)=Pm, then [S(ti,tj), F(ti,tj)]∩[S(ti,tj), F(ti,tj)]=Ø.

(5) S(ti0, PA(ti0))=0.

(6)PA(·) is a surjective function that is mapped from definition domain {0,1,…,N-1} to value domain {0,1,…,M-1}.

In the above conditions, PA(tik), S(tik, PA(tik)) and F(tik, PA(tik)) respectively denote the processor assigned starting execution time and completion execution time of task tik. The solution of Eq.(1), ti0, ti1,…, tiN-1, shows a kind of parallel task scheduling sequence. The first item in the constraints list shows that the starting time of any child tasks must be less than their parents’ completed time. The second shows the communication overhead between two tasks assigned in the same processor is zero. The third shows that completion time of a task equals to the sum of its starting time and computation time needed. The first three conditions in fact explain that the final solution must meet the definition of HeDCSs model. The fourth illustrates that when a task begins to run, it cannot be interrupted until it is finished, namely each parallel task is viewed as an atomic one in the HeDCSs. The fifth shows that tasks begin from zero point and in the last condition, the functionPAdenotes which processor is allocated to the task.

Definition 2 CPU idle time refers to execution time intervals of tasktiand its successortjin processorpm, denoted asIdle(ti,tj,pm) andIdle(ti,tj,pm)≥0.

IfIdle(ti,tj,pm)=0, it means that tasktjis immediately started when tasktiis finished, otherwise the computing procedure oftiandtjis discontinuous, namely there are time fragments of CPU that are wasted.

Definition 3S(ti,pm) represents the start time of tasktiexecuted in processorpmfor a specified scheduling scheme.

When a task has parent nodes, it begins running until all parents are completed.

Definition 4F(ti,pm) represents the completion time oftiexecuted in processorpmfor a specified scheduling schema, andF(ti,pm)=S(ti,pm)+c(ti,pm).

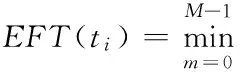
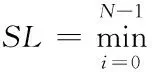
Therefore, the optimal decision for the shortest scheduling length of static tasks is equivalent to computing the shortest scheduling length of parallel tasks relationship diagram, which is a mixed integer, nonlinear programming problem with multi-variables and many constraints. Genetic algorithm has highly parallel, random and self-adaptive search performance and can solve this kind of problem more effectively.

3 Model resolution with hybrid genetic algorithm

Such traditional linear optimization as heuristic algorithm, intelligent simulated annealing algorithm, taboo search algorithm and neural network try to seek a local approximate solution or satisfactory solution. It is a fresh way to tackle the problem of task scheduling in HeDCSs by the fusion of genetic algorithm with global searching characteristics and traditional ones with fast convergence speed.

Firstly, randomly generated initial population in a solution of the problem space, then the genetic annealing operation of the initial population equation can be defined as

GASA=(S(o),A,L,R,PTP,ρ,φ,TP,ξ)

whereS(o) denotes the initial population andAis its population size,Lis the individual code length,Rrepresents selection operator,PTPis used to describe state transition of random (probability) matrix,ρis a set of genetic operator,φrepresents fitness function, TP={TPt, t=0,1,2,…, f} describes the temperature sequence,ξis the last condition of this algorithm.

When the algorithm runs, it first calculates the individual fitness function value in the initial population, in which probabilityPTPdecides whether an individual should be remained in gene pool or participated in the following hybridization evolution choice. The resulting population of genetic evolution is processed as the same rules implementing mutation operation. According to the Metropolis criterion, individuals staying in the gene pool or participating in the hybrid mutation are chosen to constantly lower their temperature. The process is repeated for each newly generated offspring, until a termination condition of this algorithm is satisfied.

3.1 Individuals with binary matrix code

Taking the scheduling sequence of tasks as an individual in the genetic algorithm, thek-th individual Gkcoded by binary matrix can be expressed as

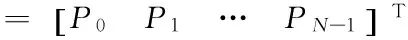
(2)

wherePidenotes the allocated processor of specified taskti,pi,mis the element in thei-th row andm-th column that showstiis placed on processorpmto run.

According to the 4-th constraint of Eq.(1), CPU is only allowed to perform a task in a period until finished, so elementpi,mcan be deduced to meet the following:

(3)

3.2 Generation of initial population

The initialization of genetic population is done by row sequences of encoding matrix of individuals and tasks are ordered afterwards by graph levels first and branches quantity later.

(1) To compute the task level. Any nodes without independence relation constitute a level in DAG, which can be calculated by

(4)

where symbolHl(ti) denotes the level of taskti,Tentryis a set of entry points, function max is to return the maximal value of definition domain andPred(ti) is also a set of parent nodes oftiin DAG.

(2) Given that there areLlevels in DAG, and thei-th level containsδinodes, all tasks can be arranged by their level grade: tγ(11), tγ(12),…, tγ(1δ1), tγ(21), tγ(22),…, tγ(2δ2),…, tγ(L1), tγ(L2),…, tγ(LδL).

(3) Tasks in each level are organized with full permutation, and then do Descartes product. The result is 2δ1-1×2δ2-1×…×2δL-1valid combinations.

(4) In view of feasibility and fairness in tasks assignment of processors, each task can be run on arbitrary processor. So, the above combinations can produce the total 2δ1-1×2δ2-1×…×2δL-1×MLinitial individuals.

3.3 Individuals adjustment measurement

Taking individual Gkas an example, specific adjustment measurements are given in the following:

Rule 1 If all tasks meet the demand of the earliest completion time, they should be unchanged.

Rule 2 If a task violates executing dependency constraints, the corresponding value in thePθ-th row should be adjusted as

① ∃ta, tβ∈T,Idle(tα,tβ,pm)≥c(ti,pm)；

② ∀γ,δ∈T,tδ∈Succ(tγ), Idle(tγ,tδ,pm)≥c(ti,pm), Idle(tγ,tδ,pm)≥Idle(tα,tβ,pm)， whereSucc(ti) is a set of successor nodes of taskti.

Generally, the start time of the task executed in the processor is affected by the computation cost, communication cost and the length of processor idle time pieces. By properly exerting above three rules to compute the finish time of tasks in each processor, the value of element in thePθ-th row corresponding to a processor that can make the task finish with earliest speed is set to 1.

3.4 The selection of fitness function

When appling the above individual adjustment measurement, only the fourth constraint is possibly unsatisfied because the parallel tasks in execution cannot be interrupted. Meanwhile in order to accelerate the convergence, the following fitness function of an individual is established

(5)

whereGkdenotes an individual in the population,Siis penalty degree while tasktiviolates the constraint that executing process cannot be interrupted,Zis set to the computational cost ofti,μis the penalty factor,mis the number of the violation of that constraint, andAis the positive constant to represent penalty coefficient whentiviolates that constraint on one time.

3.5 The definition of genetic operator

1) The selection operator

P(Gk) is the selected probability of individualGkin the genetic process, and defined as

(6)

2) The crossover operator

Step 1 Generate random crossover factorω2in [0, 1], and an integerjin [0,N-1] which denotes the position of crossover.

Step 2 Begin to crossover and produce two individualsD1,D2. The result is

Step 3 ModifyD1andD2in accordance with rules in Section 3.3, and computeF(D1) andF(D2).

Step 4 Employ a local tournament method to generate offspringO1,O2, where they satisfy the following conditions:

O1∈{C1,D1}, F(O1)=max(F(C1), F(D1)),

O2∈{C2,D2}, F(O2)=max(F(C2), F(D2)).

3)The mutation operator

Step 1 Generate a random factorβin [0, 1], and an integerγin [0, N-1] which denotes the position of mutation.

Step 2 Generate a random binary mutation factorω3from the set {0, 1}, whereω3=1 represents mutation occurrence, otherwise no variation.

Step 3 Implement mutation operation and generate offspringQexpressed as

Q=[P0C1P1C1…ω3×β×PγC1Pγ+1C1…PN-1C1]T

Step 4 ModifyQin accordance with rules in Section 3.3, and computeF(Q).

Step 5 Employ a local tournament method to generate offspringS, where they satisfy that E1∈{C1, Q}， F(S)=max(F(C1), F(Q)).

4 Performance evaluation

4.1 Performance metrics

1)Normalized schedule length (NSL)

For the convenience of analysis and fairness of comparison, a standardized processing approach is introduced and given as

(7)

whereTCPis a collection of nodes on the critical path in DAG.

2)Speedup[10]

The speedup of a parallel application is defined as

(8)

whereMis the number of processors contained in HeDCSs. Meanwhile, 1≤S≤M.

4.2 Testing environment

Hardware environment of parallel computation is composed of DELL PowerEdge series blade servers. Software communication interface is chosen to MPICH 1.5. Parallel applications are simulated by 2000 random graphs where generation parameters are seen in Table 1.

Table 1 Generation parameters of random graphs

Topcuoglu[11]has proved that among popular static algorithms in HeDCSs, HEFT and DLS are better than CPOP. Mohammad[12]further compared the performance difference between LDCP, HEFT and DLS. Through the same performance metrics used in the above work, NSL and Speedup, detailed comparison experiments between our proposed algorithm and the other three algorithms are also done.

4.3 Performance results on random graphs

1) Comparison of NSL for four algorithms

Generating 2000 DAGs with parameters from Table 1, the static task scheduling schemes are calculated respectively by the proposed algorithm, LDCP, HEFT and DLS. Furthermore, their NSL is computed by Eq.(7), the last statistical result is shown in Table 2.

Table 2 Performance results: a standardized schedule length (NSL)

Note:the data in a cell indicates comparison results on NSL using the left algorithm and the top one, including the number and proportion.

It is shown in Table 2 that for the given tested data, the number of applications whose NSL value used by the proposed algorithm is 1593, 1761, 1845, respectively, shorter than those of the LDCP, HEFT, and DLS and 79.65%, 88.05%, 92.25% of proportion respectively relative to the gross data. The proposed algorithm can shorten the execution time of a parallel application, improve the utilization performance of processors, and has general character. In addition, experiments also achieve the same result as Ref.[9], and the performance on NSL of other three algorithms is ordered by LDCP, HEFT, and DLS from high to low. Hence, correctness of the proposed algorithm is verified.

2) The influence of the generated parameters of random graphs on scheduling algorithm

In order to further validate proposed algorithm influences on different types of parallel applications, two parameters of CCR and number of task nodes are changed to randomly generate 2000 DAG again. The difference of average NSL and speedup of four algorithms is shown in Fig.1.

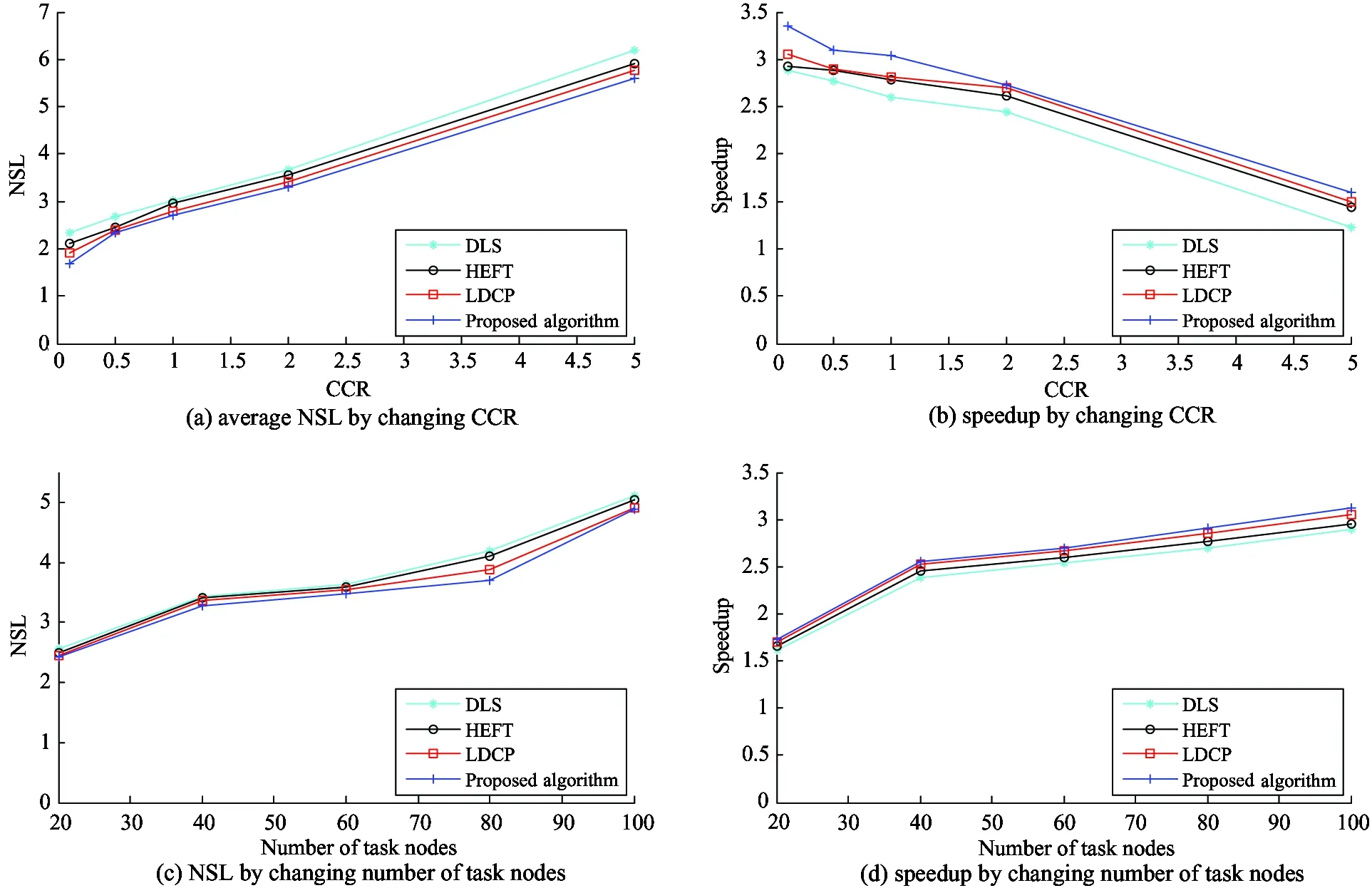
Fig.1 Effects of generation parameters of random graphs on scheduling algorithms

It is shown that the average NSL value of the proposed algorithm is shorter than those of DLS, HEFT, and LDCP by (27.03%, 19.04%, 10.52%), (11.98%, 3.68%, 2.08%), (10.89%, 9.09%, 2.87%), (10.08%, 7.30%, 3.50%) and (9.67%, 5.08%, 2.94%), respectively. The first value of each parenthesized pair is the improvement achieved by the proposed algorithm over the DLS, while the second value is the improvement over the HEFT algorithm and the last value is relative to the LDCP algorithm. This convention for representing results will be adhered throughout this paper, unless an exception is explicitly noted. The average speedup of the proposed algorithm is higher than those of DLS, HEFT, and LDCP by (15.92%, 14.73%, 9.84%), (11.91%, 7.27%, 6.90%), (16.92%, 9.35%, 8.19%), (11.89%, 4.60%, 1.11%) and (30.08%, 11.11%, 6.67%), when the CCR is equal to 0.1, 0.5, 1.0, 2.0, 5.0, respectively. In these experiments, the proposed algorithm outperforms the others on NSL, and their NSL trend is directly proportional to CCR, while their speedup is in the reverse situation. This result fully satisfies the physical meaning of CCR and indicates that the proposed algorithm is effective. On the other hand, as the number of parallel tasks increases, the NSL and speedup value of the four algorithms mentioned above become greater, but the proposed algorithm in this paper is relatively more advantageous. Experiments on random graphs conformably show that our algorithm is effective and general.

5 Conclusions

It is a challenging work in high performance computing domain for parallel task scheduling under heterogeneous distributed computing environment, which directly affects the existing resource utilization of heterogeneous computing system. In this paper, by constructing a mathematical model of static task scheduling, the tasks scheduling problem in HeDCSs is further researched, and is solved properly based on hybrid genetic algorithm. We discuss and achieve such technical details of the algorithm as individual coding, generation of initial population, individual adjustment, selection of fitness function, and definition of genetic operator, etc., and verify the generality and the effectiveness of the algorithm by abundant experiments. The further research effort is to focus on the parallelization of genetic algorithm self and influences of all generation parameters of random graphs on scheduling algorithm, therefore make further improvement on the performance and pertinence of task scheduling algorithm in HeDCSs.

[1] Nelissen G, Su H. An optimal boundary fair scheduling.Real-TimeSystems, 2014,50(4): 456-508

[2] Liu M, Chu C B, Xu Y F, et al. An optimal online algorithm for single machine scheduling to minimize total general completion time.JournalofCombinatorialOptimization, 2012,23(2): 189-195

[3] Lombardi M, Milano M. Optimal methods for resource allocation and scheduling: a cross-disciplinary survey.Constraints, 2012,17(1): 51-85

[4] Regnier P, Lima G, Massa E, et al. Multiprocessor scheduling by reduction to uniprocessor: an original optimal approach.Real-TimeSystems, 2012,2013(4): 436-474

[5] Epstein L, Hanan Z H. Online scheduling with rejection and reordering: exact algorithms for unit size jobs.JournalofCombinatorialOptimization, 2014,28(4): 875-892

[6] Darbha S, Agrawal P D. Optimal scheduleing algorithm for distributed-memory machines.IEEETransactionsonParallelandDistributedSystems, 1998,9(1): 87-95

[7] Park C I, Choe T Y. An optimal scheduling algorithm based on task duplication.IEEETransactionsonParallelandDistributedSystems, 2002,51(4): 444-448

[8] Falzon G, Li M. Enhancing genetic algorithms for dependent job scheduling in grid computing environments.JournalofSupercomputing, 2012,62(1): 290-314

[9] Arabnejad H, Barbosa J G. List scheduling algorithm for heterogeneous systems by an optimistic cost table.IEEETransactionsonParallelandDistributedSystems, 2014,25(3): 682-694

[10] Paredes R U, Cazorla D, Sanchez J L, et al. A comparative study of different metric structures in thinking on GPU implementations.LectureNotesinEngineeringandComputerScience, 2012: 312-317

[11] Topcuoglu H, Hariri S, Wu M Y. Performance-effective and low-complexity task scheduling for heterogeneous computing.IEEETransactionsonParallelandDistributedSystems, 2002,13(3): 260-274

[12] Mohammad I D, Nawwaf K. A high performance algorithm for static task scheduling in heterogeneous distributed computing systems.JournalofParallelandDistributedComputing, 2008,19(8): 399-409

Liu Yu, born in 1982. He received his Ph.D degree from Naval Engineering University in 2011. He also received his M.S. degree from Naval Aeronautical Engineering Institute in 2008. His research focuses on military modeling and simulation, operational system and high performance computing technology.

10.3772/j.issn.1006-6748.2016.02.008

①Supported by the National Natural Science Foundation of China (No. 61401496).

②To whom correspondence should be addressed. E-mail: game_liuyu@163.comReceived on Dec. 20， 2014