Quotient space model based on algebraic structure①

Chen Linshu (陈林书), Wang Jiayang, Li Li, Yang Zhenghua

(*School of Information Science and Engineering, Central South University, Changsha 410083, P.R.China) (**School of Computer Science and Engineering, Hunan University of Science and Technology, Xiangtan 411201, P.R.China) (***Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, P.R.China)



Quotient space model based on algebraic structure①

Chen Linshu (陈林书)②***, Wang Jiayang*, Li Li***, Yang Zhenghua*

(*School of Information Science and Engineering, Central South University, Changsha 410083, P.R.China) (**School of Computer Science and Engineering, Hunan University of Science and Technology, Xiangtan 411201, P.R.China) (***Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, P.R.China)

In the quotient space theory of granular computing, the universe structure is assumed to be a topology, therefore, its application is still limited. In this study, based on the quotient space model, the universe structure is assumed as an algebra instead of a topology. As to obtain the algebraic quotient operator, the granulation must be uniquely determined by a congruence relation, and all the congruence relations form a complete semi-order lattice, which is the theoretical basis of granularities’ completeness. When the given equivalence relation is not a congruence relation, it defines the concepts of upper quotient and lower quotient, and discusses some of their properties which demonstrate that falsity preserving principle and truth preserving principle are still valid. Finally, it presents the algorithms and example of upper quotient and lower quotient. The work extends the quotient space theory from structure, and provides theoretical basis for the combination of the quotient space theory and the algebra theory.

granular computing, quotient space, congruence closure, quotient operation, upper ( lower ) quotient

0 Introduction

As an age-old concept first proposed in Ref.[1], granular computing attempts to establish a formal theory to simulate human intelligence. It is a superset of fuzzy set, interval analysis, rough set, quotient space, etc., and its goal is to establish general theories and methods of solving granular problems[2-4]. The unified framework of granular computing has not been formed so far, and scholars at home and abroad have respectively established their own granular computing models from different views, which are systematically described in literatures[5-17].

The quotient space theory is a main and most important granular computing model proposed in Ref.[18], which believes that people can observe and analyze a problem in different granularities by human intelligence, and a granularity coincides exactly with a partition in mathematics, so it uses an equivalence relation (corresponding to a partition) to describe a problem’s granularity[18]. In the quotient space theory, a problem is described as a tuple (X, f,T), namely original space, where X is the set of the discussing objects, namely the universe, f is the attribute function of X, and T is the structure of X, namely universe structure or the interrelation of elements. Let R be an equivalence relation on (X, f,T), a quotient set [X]=X/R of X will be got then corresponding tuple ([X],[f],[T]) is called a quotient space of (X, f,T). The core of the quotient space theory is to get different granularities’ descriptions and properties of universe, function and structure, and to study their interrelation and interconversion. There are two basic and very important conclusions in the quotient space theory: All the different granularities form a complete semi-order lattice, which provides theoretical basis for transformation, decomposition and composition among different granularities. The granularities’ transformation keeps important characteristics—falsity preserving principle and truth preserving principle, which can greatly increase problem solving speed[2,18,19].

A significant difference from other granular computing models is that the quotient space theory has introduced the universe structure, which is more powerful to describe and solve problems. When Zhang, et al. proposed the quotient space theory, they assumed that the universe structure was a topology, and did much corresponding research, and successfully applied the model to problems solving of motion planning, temporal planning, etc.[18]. In fact, algebra is a quite important mathematical structure such as linear space, group, ring, field and lattice, and is widely used not only in mathematical fields like theories of number and category but also in other fields such as atomic physics, system engineering. In computer and information science, algebra has become a basic tool for scientific and technical personnels[11,20,21]. Wang, et al. develop the granular algebra theory, by which large-scale granular systems with complex architectures and functions can be systematically designed and analyzed[22-24]. Then, if the universe structure becomes an algebra instead of a topology, there is a problem that whether the two basic conclusions are still valid. That is to say, whether there still exists the completeness of all granularities and the characteristics preserving in granularities’ transformation.

In this study, it is supposed that the universe structure is an algebra, the concepts of congruence closure, upper quotient and lower quotient are introduced and then the completeness of all granularities, the characteristics preserving of granularities’ transformation, properties of upper/lower quotient, etc are demonstrated. The paper is organized as follows: Section 1 presents the concepts of congruence relation and congruence closure, and discusses their properties. Section 2 defines quotient operator, discusses the existing condition of quotient operator, and demonstrates that all the congruence relations form a complete semi-order lattice. Section 3 defines upper quotient and lower quotient, and discusses some of their important properties. Section 4 gives out the algorithm of upper/lower quotient. Conclusions are given in Section 5.

1 Congruence relation and congruence closure

Congruence relation and its properties are the theoretical basis of this work, and the concept of closure is widely used in mathematics. In this study, in order to discuss the existing condition of quotient operator and the existence of upper/lower quotient more easily in the viewpoint of relation, the concept of congruence closure is especially introduced. This section mainly focuses on the definitions and properties of congruence relation and congruence closure.

Definition 1 Let (X, ∘) be an algebra, where X is a universe, ∘ is a binary operator, a,b,c∈X, and R be an equivalence relation on (X, ∘). Then [a] is defined as a partition block of R including a. If R remains replaceable property under ∘, then R is defined as a congruence relation of ∘ on (X,∘), and C(R) is defined as all the congruence relations of ∘ on (X,∘). Here the replaceable property means, if [a]=[b], then for ∀c∈X, there exists [a∘c]=[b∘c],[c∘a]=[c∘b].

In an algebraic system, if there is more than one operator, it only needs to let each operator remain a replaceable property.

According to the definition of congruence relation and related knowledge, the following two conclusions[21]can be easily got. Proof is omitted.

Theorem 1 Let R be an equivalence relation on algebra (X,∘) and ∀a,b,c,d∈X. Then R is a congruence relation if and only if [a]=[b],[c]=[d]→[a∘c]=[b∘d].

Lemma 1 On algebra (X,∘), universal equivalence relation E and identity equivalence relation I must be a congruence relation.

Let R be all the equivalence relations on algebra (X,∘), and set {Rα}α⊆R, from the properties of equivalence relation, the following is got: 1) ∩αRα∈R, that is, the intersection of finite equivalence relations is still an equivalence relation. 2) t(∪αRα)∈R, that is, the transitive closure of the union of finite equivalence relations is still an equivalence relation. However, there exists a problem whether congruence relation also has the above properties.

Theorem 2 Let {Rα}α⊆C(R) be a non empty set of congruence relations on algebra (X,∘), then ∩αRα∈C(R), which means, the intersection of finite congruence relations is still a congruence relation.

Proof: Let R*=∩αRα． ∀x∈X,[x]R*=∩α[x]Rαis proved first. Then, for ∀y∈[x]R*, (x,y)∈R*, thus ∀α,(x,y)∈Rα, and so y∈∩α[x]Rα. On the other hand, for ∀y∈∩α[x]Rα, ∀α,y∈[x]Rα， thus ∀α,(x,y)∈Rα, that is, (x,y)∈R*or y∈[x]R*. Therefore, ∀x∈X,[x]R*=∩α[x]Rα．

Then it is proved R*is a congruence relation. Clearly ∀α,Rα⊇R*, so [x]Rα⊇[x]R*. Now let [a]R*=[b]R*,[c]R*=[d]R*, then for ∀α,[a]Rα=[b]Rα,[c]Rα=[d]Rα. And it is also known Rαis a congruence relation and [x]R*=∩α[x]Rα, so [a∘c]R*=∩α[a∘c]Rα=∩α[b∘d]Rα=[b∘d]R*. Therefore, R*is a congruence relation. Based on the above analysis, the theorem has been proved.

Theorem 2 is proved by Theorem 1. In the following Theorem 3 will be proved by Definition 1, Previously Lemma 2 will be introduced, which shows that element’s transitivity is also replaceable under operator ∘. Lemma 2 can be easily proved by the definition of equivalence relation, and its proof is omitted.

Lemma 2 Let R be an equivalence relation of set X, a,b,c∈X and (a,c),(c,b)∈R. Then for ∀x∈X, if (x∘a,x∘c)∈R, (x∘c,x∘b)∈R, (a∘x,c∘x)∈R, (c∘x,b∘x)∈R, there exists (x∘a,x∘b)∈R, (a∘x,b∘x)∈R．

Theorem 3 Let {Rα}α⊆C(R) be a non empty set of congruence relations on algebra (X,∘), then t(∪αRα)∈C(R), which means, the transitive closure of the union of finite congruence relations is still a congruence relation.

Proof：For ∀x1,x2∈t(∪αRα), t(∪αRα) is an transitive closure of ∪αRα, so two cases exist:

(1) (x1,x2)∈∪αRα. In this case, ∃Rα0∈{Rα}α, where (x1,x2)∈Rα0．For Rα0∈C(R), so ∀x∈X, (x∘x1,x∘x2),(x1∘x,x2∘x)∈Rα0⊆t(∪αRα).

(2) (x1,x2)∉∪αRα, but (x1,x2)∈t(∪αRα). In this case, by the definition of transitive closure, ∃y1=x1, y2,…, ym=x2∈X, where (yi, yi+1)∈∪αRα, i=1,2,…,m-1.So for ∀i,∃Ri∈{Rα}α, where ∀x∈X,(x∘yi,x∘yi+1),(yi∘x, yi+1∘x)∈t(∪αRα). By Lemma 2, ∀x∈X, (x∘x1,x∘x2),(x1∘x,x2∘x)∈t(∪αRα). Based on the above analysis, t(∪αRα) is a congruence relation.

The definition and some important properties of congruence closure are given below.

Definition 2 Let R be an equivalence relation on algebra (X,∘), if there exists a congruence relation c(R)⊇R, and for any congruence relation R′⊇R, there exists c(R)⊆R′, then c(R) is defined as a congruence closure of R.

To sum up in a word, the congruence closure of equivalence relation R is exactly the smallest one of the congruence relations which include R. Some important properties of the congruence closure is given below. Just as every binary relation has its equivalence closure, every equivalence relation also has its congruence closure, the following Lemma 3 shows the conclusion.

Lemma 3 Every equivalence relation on algebra (X,∘) has its congruence closure

Proof: Let R be an equivalence relation on algebra (X,∘), {Rα}αbe all the congruence relations including R on algebra (X,∘), and let R*=∩αRα. Clearly universal equivalence relation E⊇R, and E is a congruence relation, thus {Rα}α≠Φ. Meanwhile, for ∀α, R*⊆Rα, so if c(R)=R*is wanted, it is only needed to prove R*is a congruence relation. By Theorem 2.2, R*is a congruence relation. Therefore, c(R)=R*.

By the definition of congruence closure and Lemma 3 Lemma 4 can be got easily, proof is omitted.

Lemma 4 Let R be an equivalence relation on algebra (X,∘), then c(R)=∩R⊆Rα∈C(R)Rα.

Theorem 4 Let R be an equivalence relation on algebra (X,∘), R is a congruence relation if and only if c(R)=R.

Proof: If c(R)=R, obviously R is a congruence relation. On the other hand, if R is a congruence relation, and {Rα}αare all the congruence relations including R on algebra (X,∘), then R∈{Rα}α, thus R⊇∩αRα=c(R). And by Definition 2 R⊆c(R), therefore c(R)=R.

Theorem 5 Let R1,R2be equivalence relations on algebra (X,∘), if R1⊆R2, then c(R1)⊆c(R2). Proof: R1⊆R2, and by definition 2 R2⊆c(R2), thus, R1⊆c(R2). Clearly c(R2) is a congruence relation, so by the minimality of congruence closure’s definition, there exists c(R1)⊆c(R2).

2 Quotinet operator and completeness of granularities

In the quotient space model (X, f, T), it is assumed the universe structure is an algebra instead of a topology. Although an algebra may include more than one operator among the universe, here it is assumed there is only one binary operator ∘．And for simplicity, the attribute function f is not considered. Therefore, an original question can be simply described as an algebra (X,∘), where X is the universe, and ∘ is a binary operator.

By the above knowledge in Section 1, the existing condition of quotient operator can be discussed much easier. An equivalence relation on algebra (X,∘) matches one partition of X, and from the viewpoint of granular computing it matches a granularity. Then there exists a problem whether we can deduce a new algebraic structure on new granularity X/R, that is, whether an algebraic operator ∘′ which keeps new algebra (X/R,∘′) homomorphic to original algebra (X,∘) can be defined in Ref.[21]. The core requirement of granular computing is to get the new granularity in the case of keeping new and original structure homomorphic, because firstly it can greatly reduce the problem scale, and secondly it makes the new structure inherit some important properties of the original structure and is helpful to the computing and reasoning work in the new structure. So, it is key to research the existing conditions of quotient operator and algebraic quotient space.

Definition 3 Let R be an equivalence relation on algebra (X,∘), and p:X→X/R be a natural mapping. On quotient space X/R, if there exists an operator ∘′ which keeps p a homomorphic mapping, then ∘′ is defined as a quotient operator of X/R. Here homomorphic mapping p means, for ∀x, y∈X, p(x∘y)=p(x)∘′p(y).

In Definition 3, there is an one-to-one correspondence between quotient operator ∘′ and algebraic quotient space (X/R,∘′), that is, there exists a quotient operator ∘′ if and only if there exists an algebraic quotient space (X/R,∘′).

Theorem 6 Let R be an equivalence relation on algebra (X,∘), there exists quotient operator ∘′ on X/R if and only if c(R)=R.

Proof: By Theorem 4, the conclusion of Theorem 6 means, there exists quotient operator ∘′ on X/R if and only if R is a congruence relation. Now proof begins. On the one hand, let R be a congruence relation, then a quotient operator ∘′ can be defined on X/R, where ∀x, y∈X,[x]∘′[y]=[x∘y]. The definition is well defined, because: R is a congruence relation, and let [x1]=[x2],[y1]=[y2], thus [x1∘y1]=[x2∘y2], so [x1]∘′[y1]=[x1∘y1]=[x2∘y2]=[x2]∘′[y2], and p is a homomorphic mapping, therefore ∘′ is a quotient operator. On the other hand, let ∀x,y,w,z∈X,[x]=[y],[w]=[z], and ∘′ be a quotient operator on X/R. It is also known p is a homomorphic mapping, so [x∘w]=p(x∘w)=p(x)∘′p(w)=[x]∘′[w]=[y]∘′[z]=[y∘z], therefore, R is a congruence relation. Based on the above analysis, the theorem has been proved.

In the quotient space theory, all the equivalence relations form a complete semi-order lattice. In Theorem 6, the existing condition of quotient operator is that R is a congruence relation, in other words, in the quotient space model based on the algebraic structure a granularity is solely determined by a congruence relation. Then, there exists a problem whether all congruence relations form a complete semi-order lattice. Before discussing it, the partial order of a lattice is first defined in the following.

Definition 4 Let R1,R2be equivalence relations of set X. If R1⊆R2, then a partial order R1≤R2is defined, and R1is called smaller than R2.

Lemma 5[18]Let R be all the equivalence relations on set X, then under the partial order ”≤” in Definition 4, (R,≤) is a complete semi-order lattice.

In the quotient space theory, an equivalence relation is used to describe a granularity. Lemma 5 shows the interrelation of different granularities in quotient space theory, it is the basic and most important theorem, and it provides theoretical basis for transformation, composition, decomposition and other operations among different granularities[18,19]. In this paper, we replace the equivalence relation as a congruence relation, and also get similar conclusion as above, that is, all congruence relations form a complete semi-order lattice.

Theorem 7 Let C(R) be all the congruence relations on algebra (X,∘), then under the partial order relation ”≤” in Definition 4, (C(R),≤) is a complete semi-order lattice.

Proof: Let {Rα}αbe a subset of C(R)on algebra (X,∘). It is first proved ∩αRαis the greatest lower bound of {Rα}α. On the one hand, by Theorem 2 ∩αRαis a congruence relation. Clearly ∀α,∩αRα⊆Rα, by Definition 4, ∀α,∩αRα≤Rα, so ∩αRαis one lower bound of {Rα}α. On the other hand, let R′ be any lower bound of {Rα}α, then by Definition 4 ∀α,R′≤Rα, that is, ∀α,R′⊆Rα, so R′⊆∩αRαand R′≤∩αRα. Therefore ∩αRαis the greatest lower bound of {Rα}α, and sign inf{Rα}α=∩αRα.

Then t(∪αRα) is proved to be the least upper bound of {Rα}α. On the one hand, clearly ∀α,Rα⊆∪αRα⊆t(∪αRα), and by Theorem 3 t(∪αRα) is a congruence relation, so by Definition 4 ∀α,Rα≤t(∪αRα), therefore t(∪αRα) is one upper bound of {Rα}α. On the other hand, let R′ be any upper bound of {Rα}α, thus ∀α,Rα≤R′, that is, ∀α,Rα⊆R′, so ∪αRα⊆R′. Clearly R′ is transitive, and by the minimality of transitive closure’s definition, there exists t(∪αRα)⊆R′, that is, t(∪αRα)≤R′, therefore t(∪αRα) is the least upper bound of {Rα}α, and sign sup{Rα}α=t(∪αRα). Based on the above analysis, (C(R),≤) is a complete semi-order lattice.

In the quotient space theory, different equivalence relation corresponds to different granularity, the least upper bound and greatest lower bound of equivalence relation are also an equivalence relation, and all equivalence relations form a complete semi-order lattice[18,19]. In the quotient space model based on algebraic structure in this paper, the least upper bound and greatest lower bound of congruence relation uniquely exist, and are also an congruence relation, on which there also exists a quotient operator. Therefore, different granularities determined by congruence relations also form a complete semi-order lattice.

Definition 3 shows that the quotient space (X/R,∘′) and original space (X,∘) are homomorphic if there exists quotient operator ∘′. Then the following is got: If question a∘x=b has a solution, question [a]∘′[x]=[a∘x]=[b] has a solution, thus question [a]∘′[x]=[b] has a solution. Conversely, if question [a]∘′[x]=[b] has no solution, that is to say, [a]∘′[x]=[a∘x]≠[b], then certainly a∘x=b has no solution. These show that the falsity preserving principle is still valid in the quotient space based on the algebraic structure.

3 Definition, existence and properties of upper/lower quotient

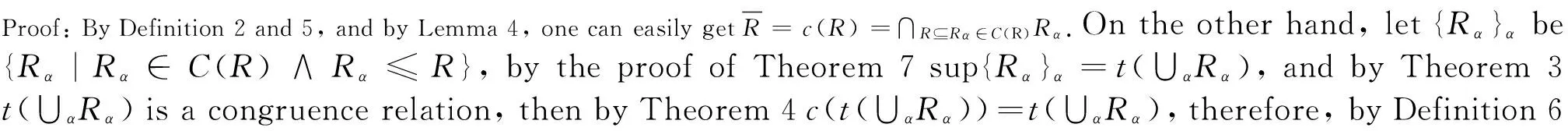
By Theorem 4, 6 and 7, it’s easy to get the following two conclusions. Proof is omitted.

Some important properties of the above operators—upper/lower congruence and upper/lower quotient are showed below.

2)By Theorem 8 clearlyR1=t(∪Rα∈C(R),Rα⊆R1Rα)⊆t(R1)=R1, and R1⊆R2, thus R1≤R2. By the maximality of lower congruence’s definition, R2is the largest one of the congruence relations which is smaller than R2, and by Theorem 3 R1is a congruence relation, therefore R1≤R2.

Theorem 9 shows that the upper /lower congruence operator possesses isotonicity, that is, if a quotient space is fine, its upper/lower quotient space is fine; if a quotient space is coarse, its upper/lower quotient space is coarse. All the quotient spaces on algebra (X,∘) form a complete lattice, on which a pair of lattice operators can be defined. In the following it gives out the definitions of the lattice operators, and discusses some important properties of the upper/lower quotient operator. These properties provide a mathematical foundation for further study on conversion and structure characters of granularities.

Definition 6 Let Q(X) be all the quotient spaces on algebra (X,∘), X1, X2∈Q(X), and R1,R2be the equivalence relations of X1,X2accordingly. Then X1∧X2is defined as the greatest lower bound of X1and X2, and X1∨X2is defined as the least upper bound of X1and X2.

From the viewpoint of partition, X1∧X2is the intersection of X1,X2, and X1∨X2is the union of X1,X2.

Theorem 10 Let X1,X2be two quotient spaces on algebra (X,∘), then:

Proof: Let R1, R2be the equivalence relations of X1, X2accordingly, and C(R) be all the congruence relations on algebra (X,∘).

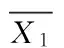
4) It first proves proposition ∪Rγ∈C(R),Rγ⊆R1∩R2Rγ⊆(∪Rα∈C(R),Rα⊆R1Rα)∩(∪Rβ∈C(R),Rβ⊆R2Rβ). For ∀(x,y)∈∪Rγ∈C(R),Rγ⊆R1∩R2Rγ, there ∃Rλ0(Rλ0∈C(R),Rλ0⊆R1∩R2), where (x,y)∈Rλ0. Because (x,y)∈Rλ0⊆R1∩R2, there exists (x,y)∈Rλ0⊆R1and (x,y)∈Rλ0⊆R2, thus (x,y)∈∪Rα∈C(R),Rα⊆R1Rαand (x,y)∈∪Rβ∈C(R),Rβ⊆R2Rβ, so (x,y)∈(∪Rα∈C(R),Rα⊆R1Rα)∩(∪Rβ∈C(R),Rβ⊆R2Rβ). Therefore ∪Rγ∈C(R),Rγ⊆R1∩R2Rγ⊆(∪Rα∈C(R),Rα⊆R1Rα)∩(∪Rβ∈C(R),Rβ⊆R2Rβ).

Then proposition t(A∩B)⊆t(A)∩t(B) can be proved, where A,B are binary relations. Clearly A∩B⊆A,A∩B⊆B, thus t(A∩B)⊆t(A),t(A∩B)⊆t(B), so t(A∩B)⊆t(A)∩t(B). Now let A=∪Rα∈C(R),Rα⊆R1Rα,B=∪Rβ∈C(R),Rβ⊆R2Rβ, based on the above proposition there exists t((∪Rα∈C(R),Rα⊆R1Rα) ∩(∪Rβ∈C(R),Rβ⊆R2Rβ))⊆t(∪Rα∈C(R),Rα⊆R1Rα)∩t(∪Rβ∈C(R),Rβ⊆R2Rβ).

On algebra (X,∘), let X1,X2be two quotient spaces on which there exist quotient operators, and R1,R2be the equivalence relations of X1,X2accordingly. Thus on the compositive quotient space X3=X1∧X2there also exists quotient operator, and the corresponding equivalence relation of X3is R1∩R2. Then, if both question [a]1∘1[x]1=[b]1and question [a]2∘2[x]2=[b]2have a solution, question [a]3∘3[x]3=[a∘x]3=[a∘x]1∩[a∘x]2=[b]1∩[b]2=[b]3is known, therefore X3=X1∧X2also has a solution. From the above analysis, if a question has a solution on quotient space X1,X2, then it also has a solution on the compositive quotient space X3of X1,X2. These show that the truth preserving principle is still valid in the quotient space model based on the algebraic structure.

4 Algorithm of upper/lower quotient

Because there is a one-to-one correspondence between equivalence relation and partition, the upper/quotient can be calculated by operation on either relation or partition. And upper quotient is the antithesis of lower quotient in definition, therefore it only discusses the algorithm of upper quotient based on the union of blocks and the algorithm of lower quotient based on iteration of relations.

4.1 The algorithm of upper quotient based on union of blocks

Based on the set theory and related knowledge, every equivalence relation corresponds and only corresponds to one partition. And a congruence relation is also an equivalence one, so it can get a partition of universe X by a congruence relation too. Then the according equivalence partition is called a congruence partition, and the corresponding equivalence block is called a congruence block.

Definition 7 Let (X,∘) be an algebra, A,B⊆X, then A∘B={x∘y|x∈A,y∈B} is defined as a product of A and B.

Algorithm1 ThealgorithmofupperquotientinafiniteuniverseInput:algebra(X,),equivalencerelationROutput:upperquotientX.Program:L1,F=X/R={A1,A2,…,Am};L2, if|F|=1thenjumptoL12;L3, fori←1to|F|L4, forj←1to|F|L5, B←AiAj;L6, fork←1to|F|L7, ifB∩Ak≠ØthenputkintosubscriptsetI;L8, if|I|≥2thendoL9, M←∪i∈IAi;L10, F←(F-{Ai|i∈I})∪M;L11, JumptoL2;L12,upperquotientX=F=X/R={A1,A2,…,At},0≤t≤m;

4.2 The algorithm of lower quotient based on iteration of relations

Definition 8 Let R1,R2be two equivalence relations of set X, then an iterative formula K using in the algorithm of lower quotient is defined as follows: ∀x, y∈X,(x, y)∈R2⟺(x, y)∈R1∧(∀z∈X,(x∘z,y∘z),(z∘x,z∘y)∈R1).

Algorithm2 ThealgorithmoflowerquotientinafiniteuniverseInput:algebra(X,),equivalencerelationROutput:lowerquotientX.Program:L1, R1←R;L2, R2←Ø;L3, foreach(x,y)∈R1L4, isElement←TRUE;L5, foreachz∈XL6, if(xz,yz)∉R1or(zx,zy)∉R1thendoL7, isElement←FALSE;break;L8, ifisElement=TRUEthendoL9, R2∪(x,y);L10,ifR2≠R1thendoL11, R2←R1;jumptoL2;L12, lowerquotientX=X/R2;

Let |R|=n, and L2-L11 is mainly considered. If R is an identity equivalence relation, L3 takes 1 time, L8 and L10 takes 0 times, and O(L3)=O(n), then the time complexity of algorithm is O(n2). Otherwise, R is a binary relation, then the number of elements in R is O(n2), that is, O(L3)=O(n2). When the algorithm is at the best, that is, R is a congruence relation, L3 takes only 1 time, and the time complexity of Algorithm 2 is O(n3). When the algorithm is at the worst, L2 and L3 take O(n) times, and similar to Algorithm 1 the time complexities of Algorithm 2 is n3+(n-1)3+…+13=n2(n+1)2/4=O(n4).

Similar to the algorithm of lower quotient based on iteration of relations, an algorithm of upper quotient can be also designed, but there are two differences between them in the following: The iterative formula is different. After getting the minimal positive integer n which makes Rn+1=Rn, Rnmust be converted into an equivalence relation, that is, the transitive closure t(Rn) of Rnshould be got, then t(Rn) is the upper congruence relation. Of the upper quotient algorithm, the iterative formula is showed in the following, and the other analysis is omitted.

Definition 9 Let R1,R2be two binary relations of set X, then an iterative formula L using in the algorithm of lower quotient is defined as follows: ∀x, y∈X,(x, y)∈R2⟺(x, y)∈R1∨(∃(x1, y1),(x2, y2)∈R1, x=x1∘x2, y=y1∘y2).

4.3 The comparison of two algorithms

Table 1 Equivalence relation R

Table 2 Algebra (X,∘)

There is a one-to-one correspondence between equivalence relation and partition which are interconvertible. An upper (or lower) congruence is also an equivalence relation, and an upper (or lower) quotient matches a partition. So, the algorithm of the upper (or lower) quotient can be designed by operation on either relation or partition, since they are inherently consistent. But in the concrete approaches, they are different. In the method of operation on partition, by merging blocks (or dividing a block) continuously, it finally gets the finest (or coarsest) grained one of the congruence partitions which are coarser (or finer) than partition X/R, which is just the upper (or lower) quotient. But in the method of operation on relation, by modifying the equivalence relation iteratively, it obtains the upper (or lower) congruence at last, by which it then gets the upper (or lower) quotient. The main differences of the above two methods can be seen from Algorithm 1, Algorithm 2 and Example 1.

Although the algorithm of upper quotient based on union of partitions can’t be directly compared with the algorithm of lower quotient based on iteration of relations, upper quotient is the antithesis of lower quotient in definitions, and the time complexities of upper quotient algorithm and lower quotient algorithm are at the same order of magnitude. Therefore, the quality of the above two methods (operation on relation or partition) can be compared by comparing Algorithm 1 and Algorithm 2. While being O(n2+m3) at the best, the time complexity of Algorithm 1 is O(mn2+m4) at the worst. But in Algorithm 2, the best time complexity is O(n3), and the worst time complexity is O(n4). In the above, |X|=n, which means n is the number of elements in universe X, |X/R|=m, which means m is the number of blocks in equivalence partition X/R, and m≤n. Thus, when m≈n, which means m=O(n), the best time complexity of Algorithm 1 is O(m3), the worst time complexity of Algorithm 1 is O(m4), and clearly the method of operation on blocks is similar to the method of operation on relations in the time complexity. But, if m≼n and m3

5 Conclusions

During many granular computing models, the quotient space model constructs granularity by equivalence relation, and different equivalence relation corresponds to different granularity[18,19], so the interrelations of equivalence relations instead of granularities can be discussed, and it is very effective and concise to study the quotient space model based on algebraic structure by equivalence relation. Given an equivalence relation on original algebraic space, one may not necessarily get an algebraic quotient operator on the quotient space, because the universe structure is not taken into account. As to obtain the algebraic quotient operator, the interrelation of elements on universe must be considered, that is, some constraints must be added to equivalence relation. It shows that the universe structure is very important in the quotient space model based on algebraic structure, because it enhances the model’s capability of knowledge expression, but it also increases the complexity of problem granularization.

In the quotient space model based on algebraic structure of this paper, a granularity is determined not by an equivalence relation but by a more stronger constraint—a congruence relation. Because all the congruence relations form a complete semi-order lattice, it still remains its completeness of granularities. In addition, the construction process of an algebraic quotient space is a homomorphic mapping, so the falsity preserving principle and truth preserving principle are still valid. These show that the two basic conclusions of quotient space theory introduced in Section 1 are still valid in the quotient space model based on algebraic structure.

The default universe structure T is assumed as a topology in the classic quotient space model proposed in Ref.[18], and it is well known that algebra is a very important and more common universe structure, so in this sence the quotient space model based on algebraic structure proposed in this work has not only extended the existing quotient space models but also provided theoretical foundation for the combination of quotient space theory and algebra theory.

[1] Jing T Y, Vasilakos A V, Pedrycz W. Granular computing: perspectives and challenges.IEEETransactionsonCybernetics, 2013, 43 (6): 1977-89

[2] Yao Y Y. Granular computing. In: Proceedings of the 4th Chinese National Conference on Rough Sets and Soft Computing, Chongqing, China, 2004. 1-5

[3] Yao Y Y. Granular computing: Past, present and future. In: Proceedings of the IEEE International Conference on Granular Computing, Hangzhou, China. 2008. 80-85

[4] Yao Y Y. The rise of granular computing.JournalofChongqingUniversityofPostsandTelecommunications(NaturalScienceEdition), 2008, 20 (3): 299-306

[5] Herbert J P, Yao J. A granular computing framework for self-organizing maps.Neurocomputing, 2009, 72: 2865-2872

[6] Panoutsos G, Mahfouf M. An incremental learning structure using granular computing and model fusion with application to materials processing. In: Proceedings of the Studies in Computational Intelligenc, Intelligent Techniques and Tools for Novel System Architectures, Heidelberg, Germany, 2008. 139-153

[7] Zhang X Y, Miao D Q. Quantitative information architecture, granular computing and rough set models in the double-quantitative approximation space of precision and grade.InformationSciences, 2014, 268(2): 147-168

[8] Wang J, Deng L, Zhang C. The research on computing dynamic reduct. In: Proceedings of the IEEE International Conference on Granular Computing (GrC), Hangzhou, China, 2012. 504-509

[9] Wang J, Zhou J. Research of reduct features in the variable precision rough set model.Neurocomputing, 2009, 72 (10): 2643-2648

[10] Wang J, Peng L. Research on expression of rough equality sets. In: Proceedings of the Pacific-Asia Workshop on Computational Intelligence and Industrial Application PACIIA′08, Wuhan, China, 2008, 1: 337-341

[11] Wang J Y, Yang Z H. A comparative study of quotient space model with Two structures.JournalofElectronics, 2013, 41(11): 2262-2269. (In Chinese)

[12] Pedrycz, Witold, Kwak K C. Boosting of granular models.FuzzySetsandSystems157, 2006, 157(22): 2934-2953

[13] Tan X, Lin G. Granular computing based on multi-complex data.JournalofComputationalInformationSystems, 2012, 16(8): 6895-6901

[14] Zhao L, Xue Z. Generalized dominance-based set approach to security evaluation with imprecise information.HighTechnologyLetters, 2010, 16(3): 254-262

[15] Zeng Y, Liang X W, Li Y. A distributed routing algorithm based-on simplified topology in LEO satellite networks.HighTechnologyLetters, 2010, 16(2): 117-123

[16] Ren B, Zhang S Y, Shi Y D. The partition and regeneration of multi-granularity transplantable structures for structural variant design.ChineseHighTechnologyLetters, 2012, 22(1): 100-105. (In Chinese)

[17] Meng Z Q, Shi Z Z. Self-adaptive image semantic classification based on tolerance granular space model.ChineseHighTechnologyLetters, 2012, 22(7): 697-705. (In Chinese)

[18] Zhang L, Zhang B. Theory and applications of problem solving. 2nd Edition. Beijing: Tsinghua University Press, 2007. (In Chinese)

[19] Zhang Y P, Zhang L, Wu T. The representation of different granular worlds-a quotient space.ChineseJournalofComputers, 2004, 27(3): 328-333. (In Chinese)

[22] Wang Y X. On system algebra: a denotational mathematical structure for abstract systems modeling.InternationalJournalofCognitiveInformaticsandNaturalIntelligence, 2008, 2 (2): 20-43

[23] Wang Y X, Zadeh L A, Yao Y. On the system algebra foundations for granular computing.InternationalJournalofSoftwareScienceandComputationalIntelligence, 2009, 1(1) : 64-86

[24] Wang Y X. Granular algebra for modeling granular systems and granular computing. In: Proceedings of the IEEE International Conference on Cognitive Informatics, Hong Kong, China, 2009. 145-154

Chen Linshu, born in 1981. He is working for Ph.D degree in School of Information Science and Engineering, Central South University, Changsha, China. His research interest is granular computing and intelligent information processing.

10.3772/j.issn.1006-6748.2016.02.007

①Supported by the National Natural Science Foundation of China (No. 61173052) and the Natural Science Foundation of Hunan Province (No.14JJ4007).

②To whom correspondence should be addressed. E-mail: chen-lin-shu@163.comReceived on June 4， 2015