Distributed cubature Kalman filter based on observation bootstrap sampling①

Hu Zhentao (胡振涛), Hu Yumei, Zheng Shanshan, Li Xian, Guo Zhen

(Institute of Image Processing and Pattern Recognition, Henan University, Kaifeng 475004, P.R.China)



Distributed cubature Kalman filter based on observation bootstrap sampling①

Hu Zhentao (胡振涛), Hu Yumei②, Zheng Shanshan, Li Xian, Guo Zhen

(Institute of Image Processing and Pattern Recognition, Henan University, Kaifeng 475004, P.R.China)

Aiming at the adverse effect caused by observation noise on system state estimation precision, a novel distributed cubature Kalman filter (CKF) based on observation bootstrap sampling is proposed. Firstly, combining with the extraction and utilization of the latest observation information and the prior statistical information from observation noise modeling, an observation bootstrap sampling strategy is designed. The objective is to deal with the adverse influence of observation uncertainty by increasing observations information. Secondly, the strategy is dynamically introduced into the cubature Kalman filter, and the distributed fusion framework of filtering realization is constructed. Better filtering precision is obtained by promoting observation reliability without increasing the hardware cost of observation system. Theory analysis and simulation results show the proposed algorithm feasibility and effectiveness.

state estimation, cubature Kalman filter (CKF), observation bootstrap sampling, distributed weighted fusion

0 Introduction

The state estimation problems of a nonlinear system widely exist in the field of signal processing, integrated navigation, target location and tracking, etc[1]. The implementation principle for existing state estimator is, under the framework of recursive Bayesian estimation, to take the advantage of all observation information to construct a state posterior probability distribution function, and then to obtain state optimal estimation according to the minimum variance criterion. While Kalman filter (KF)[2]is the typical implementation for linear Gaussian system. However, with regard to nonlinear features of estimated system, the optimal solution usually cannot be resolved. Therefore, a large number of suboptimal approximation algorithms are proposed such as the extended Kalman filter (EKF)[3,4], of which realization mechanism is to realize the local linearization of state equation and observation equation. It only calculates the posterior mean and covariance accurately to the first order with all higher order moments truncated. If the estimated system nonlinearities are very strong, EKF usually can not obtain good filtering result and even lead to filtering divergence phenomenon[5].

Considering that the probability density distribution is easier to be approximated than nonlinear function[6], the application of sampling method for approximating posterior probability distribution to solve the state estimation problem of nonlinear system is increasingly attracting widely attention. The sampling method is mainly divided into two categories: stochastic sampling and deterministic sampling. The stochastic sampling nonlinear filter, namely particle filter (PF)[7,8], is a kind of Monte Carlo method. In the filtering process, a set of stochastic points with weight, sampled from the state space, are adopted to approximate state probability density function. As a result, the optimal estimation is approximated highly, and it needs not to be subject to the constraints of linear and Gaussian assumption. However, a large number of particles are needed to ensure the filtering precision and convergence, the calculation of stochastic sampling nonlinear filter is heavier than deterministic sampling filter. Moreover, the stochastic sampling mechanism often leads particles to degeneracy after a few iterations. The adverse effect caused by particle degeneracy is mitigated in a certain degree through re-sampling, but the re-sampling process results in the reduction of particles diversity. The typical implementation of deterministic sampling filter mainly includes unscented Kalman filter(UKF)[9,10]and cubature Kalman filter (CKF)[11,12]. UKF approaches nonlinear state posterior distribution by UT transformation strategy, and it has higher universality for nonlinear system with Gaussian noise. But whether the selection parameter is reasonable or not in UKF, it affects the estimation precision of system state directly. In addition, the problem that filtering variance is not positive definite may occur. In essence, a third-degree spherical-radial cubature rule to compute integrals numerically is derived in CKF. Nonlinear state posterior distribution is approximated through a set of points with deterministic space position distribution and weight. In the process of sampling and filtering, the weight in CKF is positive, so as to ensure that the filtering covariance is positive definite matrix.

The distributed weighted optimal fusion technology is one of the effective methods to improve state estimation precision. Through the synergy between sensors to extend the measuring range, improving the information redundancy and credibility, and then the objective of improving state estimation precision is achieved. The fusion structure includes the centralized, distributed and hybrid while the distributed structure with fault-tolerant is the popular method used in implementation. In addition, achieving multi-source information will inevitably lead to the increase of the burden of hardware resource (especially sensor). Aiming at improving filtering precision without increasing hardware cost, realization of the distributed filter for nonlinear system state estimation has always been focused by experts and scholars in related field. To solve the above problem, an observation bootstrap strategy has been designed through combining the latest observation with the prior statistical information from observation noise modeling. On this basis, the bootstrap observation set is built and then applied to CKF filtering framework. Combined with distributed weighted optimal fusion technology[14,15], a novel distributed cubature Kalman filter based on observation bootstrap sampling (DCKF-OBS) is proposed. Its advantage is to improve state estimation precision without increasing hardware cost (the number of sensor and accuracy), through reducing the uncertainty of latest observation information.

1 Observation bootstrap strategy

Considering the general nonlinear discrete-time dynamical system, the system equation and observation equation are given as follows:

xk=f(xk-1)+wk-1

(1)

zk=hk(xk)+vk

(2)

Aiming at reducing the adverse effect caused by the uncertainty and unicity of single sensor observation, the bootstrap sampling points of sensor observation are obtained through improving the degree of freedom according to the observation bootstrap strategy:

(3)

(4)

(5)

2 Cubature Kalman filter

The optimal solution to solve nonlinear filtering problem needs to get a complete description of conditional probability density function. In CKF implementation, a third-degree spherical-radial cubature rule is extended to compute a standard Gaussian weighted integral of f(x) as follows. As a result, conditional posterior probability is obtained[13]:

(6)

Step A Time update step

1) Evaluate cubature points

Pk|k=Sk|k(Sk|k)Τ

(7)

(8)

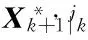
(9)

(10)

(11)

Step B Observation update step

1) Evaluate cubature points

Pk+1|k=Sk+1|k×(Sk+1|k)Τ

(12)

(13)

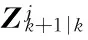
(14)

(15)

(16)

(17)

4) Evaluate the filtering gain Kk+1at time k+1

(18)

(19)

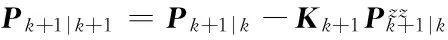
(20)

In essence, the nonlinear state posterior distribution is approximated through a set of points with deterministic space position distribution and weight in CKF. In the process of sampling and filtering, weight in CKF is positive all the time, which ensures that the estimate covariance is positive definiteness. In addition, in the aspect of real-time, because of deterministic sampling and less samples, CKF is superior to PF. In the aspect of precision, the numerical integral based on third-degree spherical-radial cubature rule is adopted in CKF, to approximate Gaussian weighted integral. Its approximation precision of probability distribution after nonlinear transformation is superior to UKF adopted unscented transformation[13].

3 Distributed cubature Kalman filter based on observation bootstrap sampling

In the distributed state fusion structure, each sensor observation is assigned to one estimator independently, namely taking use of the observation of each sensor to filter, then the local estimation is delivered to the center node for fusion. The global state estimate and its covariance are given as

(21)

(22)

(23)

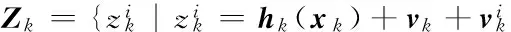
1.Initializestateestimationanditserrorcovariance^xi0|0=x0andPi0|0=P0.2.GeneratethebootstrapobservationsetZk+1accordingtoEq.(3).3.Calculatethelocalestimation^xik+1|k+1anditserrorcovariancePiik+1|k+1,accordingtophysicalobservationzk+1,bootstrapobservationsetZk+1andEq.(7)toEq.(20).Notethatthebootstrapobservationerrorco-varianceisgivenasPzzk+1|k=∑Li=1Zjk+1|k(Zjk+1|k)Τ/L-^zk+1|k(^zk+1|k)Τ +σ2vk+1+λσ2vik+1.4.Solvetheglobalestimation^xgk+1|k+1ac-cordingtoEq.(21)toEq.(23).5.Let^xk+1|k+1=^xgk+1|k+1andPk+1|k+1=Pgk+1|k+1,sothecurrentstateestimationisobtained.6.IncreasekandcontinuetoStep2.

4 Simulation result and analysis

To verify the validity of DCKF-OBS, the Monte Carlo simulations of target tracking are presented in the Cartesian coordinate system. It adopts the typical uniform motion model and nonlinear observation model, and the number of Monte Carlo is 200. The root mean square error(RMSE) is used to evaluate the property of the algorithm in filtering precision. In this simulation environment, motion state equation and observation equation are given as

xk=Fk|k-1xk-1+Γk-1wk-1

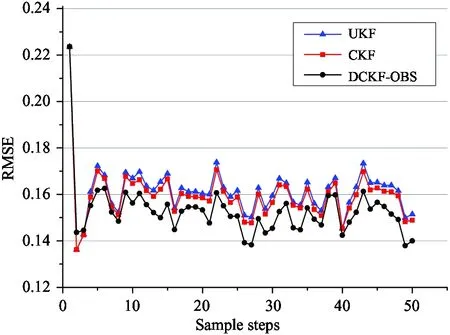
Fig.1 Horizontal direction

Fig.2 Vertical direction

The quantitative comparison of mean state estimation RMSEs of the three algorithms are given in Table 1. The number of bootstrap observation is 30, and it is known clearly that the RMSE value of DCKF-OBS is the lowest. Fig.1, Fig.2 and Table 1 all indicate that the mean value of the RMSEs of DCKF-OBS is the lowest. The filtering precision of CKF is higher than UKF, and the DCKF-OBS is superior to the others. The analysis is elaborated in Section 2 and Section 3.

Table 1 The RMSEs comparison when the number of bootstrap observation is 30

The comparison of the mean value of state estimation RMSEs is given in Fig.3 and Fig.4 in the condition of different number of bootstrap observation. As shown in the figures, with the number of bootstrap observation increasing, the mean value of state estimation RMSEs decreases. At the stage of bootstrap observation number from 5 to 35, the mean value of RMSEs decreases sharply, and state estimation precision increases obviously. At the stage of bootstrap observation number from 35 to 50, the mean value of RMSEs is flat. Namely the effect on enhancing state estimation precision through increasing the number of bootstrap observation is slight. Moreover, with the increasing number of bootstrap observation, the hardware undertakes a larger amount of calculation. Therefore, performance indexes such as precision, real-time and calculation should be considered in practice. So as to select the appropriate number of bootstrap observation involved in filtering, and as a result, the superior precision of system state estimation is achieved. The RMSEs quantitative comparison of DCKF-OBS is given in Table 2 with different number of bootstrap observation.

Fig.3 Horizontal direction

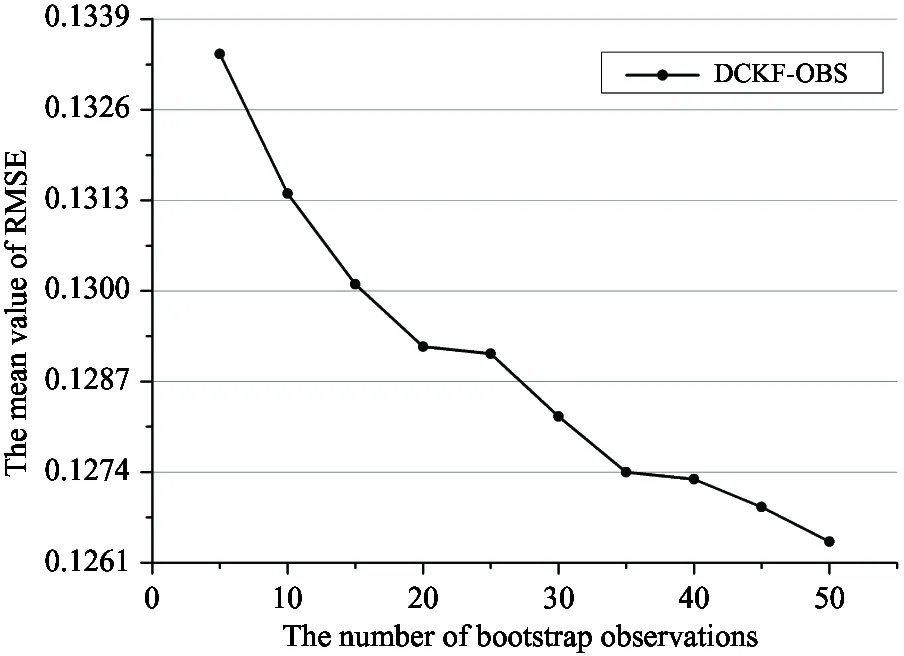
Fig.4 Vertical direction

Table 2 The RMSEs comparison of DCKF-OBS with different number of bootstrap observation

5 Conclusions

The estimation of nonlinear system is a widely considered field in engineering application, while the filter algorithm and the sensor accuracy are two dominant factors influencing the state estimation precision. Considering the two factors above, a novel distributed cubature Kalman filtering algorithm based on observation bootstrap sampling is proposed under the condition of single sensor observation system. In this algorithm, firstly, on the basis of physical observation, the bootstrap observation set of system state is obtained though bootstrap strategy. Secondly, the physical observation and bootstrap observation respectively participate in cubature Kalman filtering process, so that the local state estimation is achieved. And then global state estimation is achieved through adopting the information fusion theory to fuse local state estimations. The simulation experiments indicate that the DCKF-OBS is superior to CKF by comparing the state estimation RMSE. Furthermore, the state estimation precision is improved continually, along with the increase of the number of bootstrap observation. While the number is greater than 15, the state estimation precision increases slightly. The algorithm applies to nonlinear non-Gauss state estimation problem with single sensor observation system.

[1] Xu S , Su X X, Liu S G. Dimension-wise adaptive spare grid quadrature nonlinear filter.ActaAutomaticaSinica, 2014, 40(6): 1249-1264

[2] Nikoukhah R, Campbell S L, Delebecque F. Kalman filtering for general discrete-time linear systems.IEEETransactionsonAutomaticControl, 1999, 44(10):1829-1839

[3] Gustafsson F, Hendeby G. Some relations between extended and unscented Kalman filters.IEEETransactionsonSignalProcessing, 2012, 60(2): 545-555

[4] Huang S, Dissanayake G. Convergence and consistency analysis for extended Kalman filter based SLAM.IEEETransactionsonRobotics, 2007, 23(5): 1036-1049

[5] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation.ProceedingsoftheIEEE, 2004, 92(3): 401-422

[6] Wang X, Liang Y, Pan Q, et al. Nonlinear Gaussian smoothers with colored measurement noise.IEEETransactionsonAutomaticControl, 2015, 60(3): 870-876

[7] Hu Z T, Liu X X, Hu Y M. Particle filter based on the lifting scheme of observations.IETRadar,Sonar&Navigation, 2014, 9(1): 48-54

[8] Cappe O, Godsill S J, Moulines E. An overview of existing methods and recent advances in sequential Monte Carlo.ProceedingsoftheIEEE, 2007, 95(5): 899-924

[9] Gustafsson F, Hendeby G. Some relations between extended and unscented Kalman filters.IEEETransactionsonSignalProcessing, 2012, 60(2): 545- 555

[10] Chang L B, Hu B Q, Li A , et al. Transformed unscented Kalman filter.IEEETransactionsonAutomaticControl, 2013 ,58(1): 252-257

[11] Arasaratnam I, Haykin S, Hurd T R. Cubature Kalman filtering for continuous-discrete systems: theory and simulations.IEEETransactionsonSignalProcessing, 2010, 58(10): 4977-4993

[12] Ding Z, Balaji B. Comparison of the unscented and cubature Kalman filters for radar tracking applications. In: Proceedings of the IET International Conference on Radar Systems, Glasgow, UK, 2012. 1-5

[13] Arasaratnam I, Haykin S. Cubature Kalman filters.IEEETransactionsonAutomaticControl, 2009, 54(6): 1254-1269

[14] Han C Z, Zhu H Y, Duan Z S. Multi-source Information Fusion. Beijing: Tsinghua University Press, 2010. 43-49 (In Chinese)

[15] Bar-Shalom Y, Willett P K, Tian X. Tracking and Data Fusion: A Handbook of Algorithms. Storrs: YBS Publishing, 2011

Hu Zhentao, born in 1979. He received his Ph.D degree in Control Science and Engineering from Northwestern Polytechnical University in 2010. He also received his B.S. and M.S. degrees from Henan University in 2003 and 2006 respectively. Now, he is an assistant professor of College of Computer and Information Engineering, Henan University. His research interests include complex system modeling and estimation, target tracking and particle filter, etc.

10.3772/j.issn.1006-6748.2016.02.005

①Supported by the National Natural Science Foundation of China (No.61300214), the Science and Technology Innovation Team Support Plan of Education Department of Henan Province (13IRTSTHN021), the Post-doctoral Science Foundation of China (No.2014M551999), and the Funding Scheme of Young Key Teacher of Henan Province Universities (No.2013GGJS-026).

②To whom correspondence should be addressed. E-mail: hym_henu@163.comReceived on Apr. 1， 2015