基于出行时段的高速铁路列车配流方法

翁湦元，单杏花

（中国铁道科学研究院 电子计算技术研究所, 北京 100081）

基于出行时段的高速铁路列车配流方法

翁湦元，单杏花

（中国铁道科学研究院 电子计算技术研究所, 北京 100081）

分析高速铁路客流在不同时段的分布特点，以及客流分布与列车服务频率的关系，在此基础上定义由出行时段费用和车厢拥挤程度费用组成的广义旅客出行费用，构建高速铁路列车配流的用户均衡模型，并给出 Logit 随机网络加载算法结合相继平均法的求解算法。根据构建的配流模型，以上海虹桥到北京南、上海虹桥到南京南的 OD 客流为例进行客流分配，验证了模型的有效性。

高速铁路；客流分配；用户均衡模型；Logit 算法；相继平均法

1高速铁路客流时间分布特性分析

由于列车运行图变化频繁，对于客流在不同车次分布规律的研究将在一定程度上受到运行图调整的干扰，因而在现有客流数据的基础上分析客流在时间上的分布特性，更能作为旅客出行行为特性的参考依据。对比 30 min、60 min 及 120 min 为间隔的客流时段分布数据，可知 60 min 间隔的客流时段分布数据较为平滑，又比 120 min 间隔的数据拥有更多细节，因而选择 60 min 作为时段间隔。由于每日客流总量随日期的波动[1]，在研究不同时段旅客的选择倾向的时候，应排除客流总量波动的影响。因此，研究不同时段客流占当日总客流的比例可以更准确地反映出旅客的选择倾向。

1.1时段客流比例分析

选取京沪高速铁路 (北京南—上海虹桥) 上海虹桥到北京南、南京南的 OD 客流进行分析。

（1）分席别时段客流比例均值分布情况。2014年上海虹桥到北京南、南京南不同时段的各席别客流占当日总客流比例平均值分布情况如图 1 所示，可以看出不同席别的时段客流分布比例基本相同。

（2）不同星期日期的时段客流比例均值分布情况。上海虹桥到北京南、南京南各星期日期的时段客流占当日总客流比例平均值的分布情况如图 2 所示，可以看出时段客流占当天客流总量的比例分布受星期日期特性影响，其客流分布有一个较为明显的特点，即周日客流在上午所占比重偏低而周五客流在下午所占比重偏高。不同星期日期的时段客流分布规律，能在一定程度上作为配流建模的参照。

图 2 各星期日期分时段 OD 客流分布

1.2客流分布及列车服务频率分析

为反映节假日前后每日时段客流分布的变化情况，截取 2014 年春节前后 (1 月 26 日—2 月 7 日) 上海虹桥—北京南、上海虹桥—南京南的 OD 客流及列车服务频率数据进行分析，分析结果分别如图 3、图 4 所示。①从时段客流分布比例上看，上海虹桥到北京南的客流在春节前期更多分布于上午，而春节后期倾向于下午但区别并不明显；上海虹桥到南京南的客流在春节前期更多分布于下午，而春节后期集中于上午。②从列车服务频率上看，各时段分布频率随日期的推移有一定的变化，但没有明显的规律；上海虹桥到南京南的客流在春节后期上午时段的发车频率高于下午。

图 3 上海虹桥—北京南时段客流与列车服务频率比例示意图

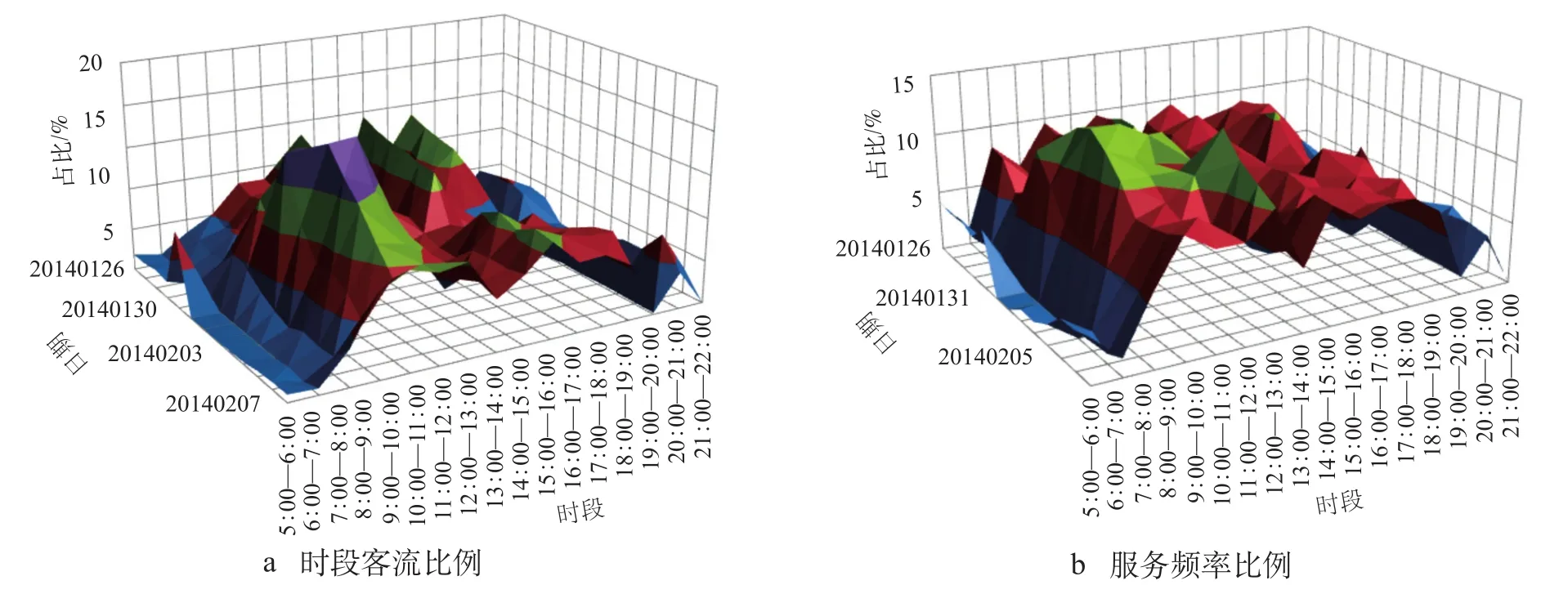
图 4 上海虹桥—南京南时段客流与列车服务频率比例示意图

综合以上 2 组数据，可以看出每日时段客流比例分布特性与节假日属性相关。在部分场合下列车服务频率对时段客流分布有一定影响，但客流分布比例的变化并不完全随列车服务频率变化。因此，客流的时间分布特性可以在一定程度上作为旅客出行行为特性的参考依据。

2基于出行时段的高速铁路列车配流模型建立与求解

2.1配流模型构建

2.1.1配流问题描述

在已知 OD 交通量、网络图及交通网络中各路径阻抗函数的情况下，将 OD 交通量正确合理地分配到各个路径上就是客流分配 (以下简称“配流”)所需解决的问题[2]。配流问题是高速铁路列车开行方案调整和优化所需研究的重要课题，配流结果是开行方案调整和优化的重要依据。

影响旅客对出行路径选择的因素多种多样，有出行时间、行程距离、席别、票价、路途拥挤程度等，旅客对各影响因素的认知与预测各不相同，因而旅客对路径的选择不存在普遍的计算法则。对客流的分配是建立在某些假设之上的，正确的交通量分配方法应能较好地模拟与再现现实的客流分布状态。实际铁路客运网络中有很多 OD 对，OD 间包含的多条路径通常由很多路段组成，而路段往往被包含在多个 OD 对的路径之中相互重叠。因此，实际客运网络的均衡状态十分复杂。在铁路客运网络中，假设每个 OD 对间不同车次、不同运行时间、不同席别、不同票价都是不同的路径，则 OD间往往存在多条路径，当客流较少时，旅客倾向于选择阻抗最小的路径；随着客流的逐渐增加，最短路径的流量也在增加，进而增加了该路径的出行阻抗，阻抗增大到一定程度而变为非最短路径后，旅客将会转而选择新的最短路径。随着流量的增加，OD 间的所有路径都有可能被旅客选择。

2.1.2配流问题研究现状

由于配流问题的复杂性，如何建立合理的客流分配模型，以及如何对模型进行求解，成为整个交通流规划中的重点问题。对于客流分配模型，目前国内外有较多研究成果，其模型大致分为均衡模型和非均衡模型[3]。早期模型主要是非均衡模型，包括转移曲线分配法、时间比例分配法、马尔可夫链法等，这些非均衡模型使用的数学模型较为简单，精度较低，不能很好地反映现实客流的分布。1952 年学者 Wardrop 提出交通网络平衡定义的第一原理和第二原理，奠定了交通流分配理论的基础。其提出的第一原理通常简称为 Wardrop平衡，在实际交通流分配中也称为用户均衡 (User Equilibrium，UE) 或用户最优。

用户均衡模型是用户对换乘网络的所有信息完全可知的情况下，使自己做出成本最小的选择。而实际情况中，由于影响出行的各类因素繁多，用户无法得到线路的所有信息，因而旅客出行时，对于线路的选择将具有一定的随机性。相对于用户均衡而言，随机用户均衡 (Stochastic User Equilibrium，SUE) 配流模型综合了随机分配和 Wardrop 平衡的概念，可以获得更加符合实际的交通流分配结果。随机用户均衡与一般用户均衡条件相比，更具有普遍性，而用户均衡条件是随机均衡问题的特例。

2.1.3用户均衡模型的数学描述

交通网络的基本要素包括：①起点 (Origin)；②终点 (Destination)；③OD，即起点与终点的合称，表示一次出行过程的开始和结束地点；④节点，交通网络中的节点代表路口、车站或者区域中心等；⑤路段，即连接不同节点的弧，代表节点间的道路或者交通方式；⑥路径，即乘客完成出行过程中在路网上连续移动经过的路段集合。

Bechmann 于 1956 年提出交通网络均衡问题的数学描述如下[2]。

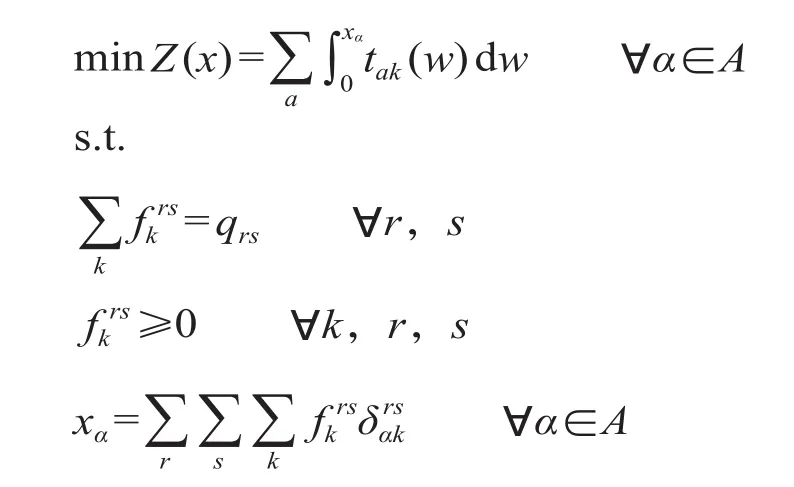
式中：Z (x) 为目标函数，目标为所有路段阻抗函数的积分和最小，即系统最优状态；α 为路段编号；tak(w) 为路径 k 中路段 α 的阻抗函数；xα为路网中路段 α 上的总叠加流量；为 OD 对 r，s 之间第 k 条路径上的流量；qrs是 r，s 之间的出行需求；为路段与路径之间的相关系数，若路段 α 在 OD 对 r， s 之间的第 k 条路径上，则，否则；A 为路网上所有路段的集合。

2.2广义旅客出行费用定义

旅客根据旅行时间、便捷程度等因素来选择出行行为。为了量化地研究旅客的选择行为，将影响旅客选择的各种因素以费用函数的形式表现出来，而旅客将倾向于选择费用较低的出行方案[2]。在某路径范围内，考虑 N 种影响因素的旅客出行广义费用的表达式如下。

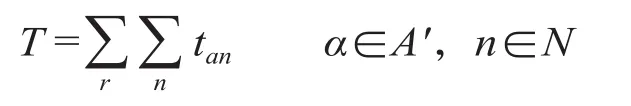
式中：T 为旅客选择某条路径的总费用；a 为该路径中的一个路段；tan表示第 n 种影响因素在 a 路段中的费用函数；N 为影响路径费用计算的因素集合；A' 为某路径所包含的全部路段集合。

2.2.1出行时段费用

旅客的出行选择倾向在当日不同时段下有明显的区别[4]，该倾向可以通过不同时段客流量占当日总客流量的比例来反映，客流比例高的时段表明所对应的出行费用相应较低，旅客选择该时段的概率更高；而不同时段的选择概率分布情况与当日的星期、节假日属性相关。依据交通客流时空分布特性理论，将出行时段费用与时段客流分布比例的关系表述如下[1]。

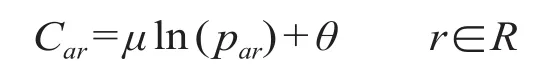
式中：Car为 a 路段在 r 时段的出行费用；par为 a 路段在 r 时段的客流分布比例参考值；R 为 OD 间所有有效时段；μ，θ 为函数调整系数。

2.2.2车厢拥挤费用

除了出行时间外，旅客在有多车次可选的情况下，车厢的拥挤程度也是影响旅客选择的因素[5]。随着车厢的拥挤程度上升，旅客的乘坐舒适度也随之下降，旅客更加倾向于选择较不拥挤的车次。同时，当列车服务频率提高时，在相同拥挤费用下，客流量也随之提高。美国联邦公路局在对大量路段进行调查的基础上得到了用于表达行驶时间和路段交通量之间关系的表达式，即 BPR 函数。依据拥挤效应的理论，可以借助 BPR 函数来表示拥挤程度对旅客舒适度造成的影响[5]。式中：a 表示旅客在 OD 间经过的路段，a ∈ A；ta(xa)表示路段 a 上当客流量为 xa时的费用函数；ta(0) 表示路段 a 的最小费用；Xa表示路段 a 的最大载客量；α，β 分别为 BPR 函数的参数；θ 表示随机误差。α，β 的不同取值，可以反映出不同人群对于拥挤程度的敏感程度，其取值一般为 α = 2.62，β = 5。

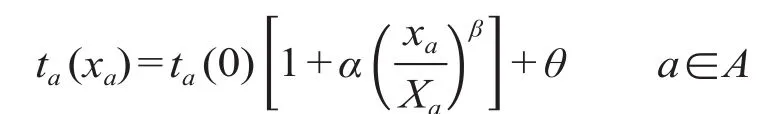
2.2.3旅客出行广义费用函数

结合上述 2 种费用描述，旅客在路段的出行广义费用函数表达如下。

2.3模型求解

2.3.1配流算法

（1）Logit 路径选择概率模型。根据用户均衡模型原理，旅客总是选择费用最低的路径出行。路径选择问题实际上就是旅客选择路径的概率问题，通常使用的算法为 Logit 随机网络加载模型算法[6]。该算法在已知 OD 对间路径信息情况下，将客流分配到有效的路径上。假设路径的费用阻抗的随机分布是确定的，则可以根据费用的分布来计算旅客选择的概率。根据最低费用原理，某条路径被旅客选择的概率就是这条路径在所有有效路径中对该乘客费用最低的概率。旅客选择第 k 条路径的概率可以用下式表示。

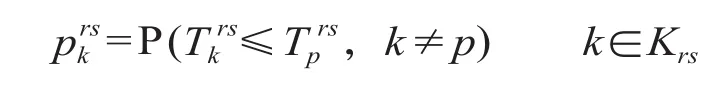
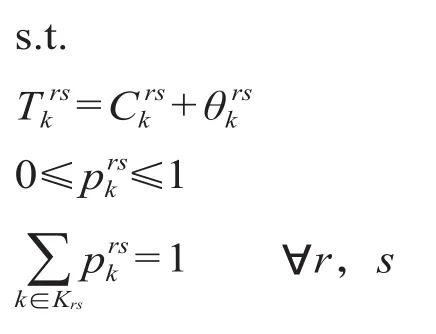
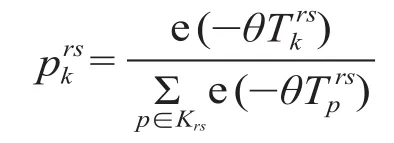
当对所有有效路径进行上述计算后，各路径的分配概率即为 OD 客流在各路径上的流量分配比例。

（2）相继平均法[8]。Logit 模型只考虑路径阻抗之间的绝对差别，并没有考虑客流在加载过程中导致的路径阻抗的变化。在假设旅客的路径选择行为服从 Logit 模型的决策过程的前提下，使用相继平均法加载客流来模拟旅客出行行为的逐步演化过程，并求解稳定的配流结果，步骤如下。

①确定有效路径集合。

②初始化，置迭代次数为 1。

③根据 Logit 决策模型进行随机配流。

④使用相继平均法迭代计算。

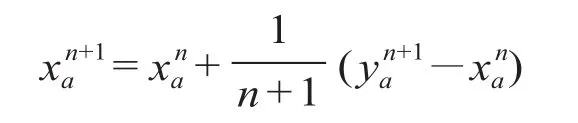
⑤收敛性检查。每次迭代后均计算与上次迭代的收敛偏差，在偏差满足收敛条件或者达到最大迭代次数的时候停止迭代，即

2.3.2 广义出行费用计算

（1）OD 间路径拓扑结构设计。为简化计算模型，仅考虑 OD 直达客流，则 OD 间的换乘网络简化为 2 点间的路径集合，如图 5 所示。其中，Link 记录了路径的相关信息，包括列车始发日期、车次、出发时间、到达时间、席别、路程长度、最大客流等。Link 的划分应按照计算精度要求而定，并具备属性值组合的唯一性，如果仅需计算某车次的配流数量，则应该把席别属性从 Link 中排除，并且同一日期不应出现 2 条相同车次的 Link。

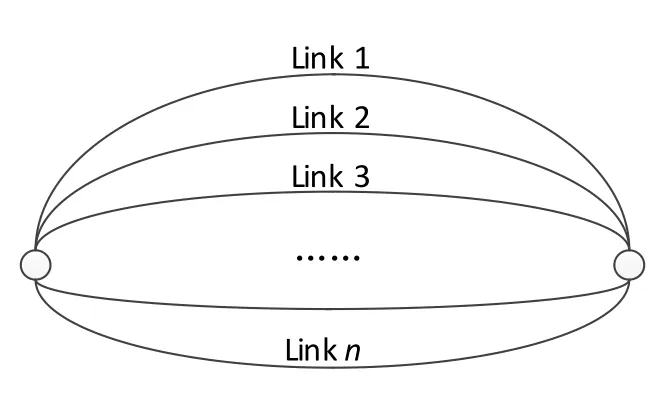
图 5 OD 路径拓扑结构示意图

（2）费用函数计算。在列车运行图已知的情况下，Link 数量和每一 Link 的属性已知。在每次配流迭代计算中应分别对每个 Link 计算其广义出行费用。①对于时段费用，根据目标日期的属性查询历史数据，并确定目标日期的时段费用，如果为农历节假日则取往年节假日对应日期的时段客流比例数据，如果为非节假日则获取往年对应日期前后 3 周的对应星期的时段客流数据的平均值，将得到的时段客流比例作为时段费用计算的变量 par即可得出该 Link 的时段费用。②对于拥挤费用，从运行图中获取各车次在目标日期的定员数据，并将各车次的定员数据汇总至所属 Link，汇总求和即可得到每个Link 的最大载客量，即 Xa。结合每次迭代的随机配流结果，即 xa，可计算各 Link 在每次配流迭代计算中的拥挤费用。

2.3.3求解计算流程

配流的计算流程分为输入参数、费用计算、配流迭代 3 个阶段。输入参数阶段取得配流计算日期、OD 客流总量预测值、有效 OD 信息等；费用计算阶段通过历史客流数据作为客流时段费用分布数据计算的依据；配流迭代阶段使用 Logit 随机配流及相继平均法进行迭代计算，最终获得客流分配结果。配流计算流程如图 6 所示。

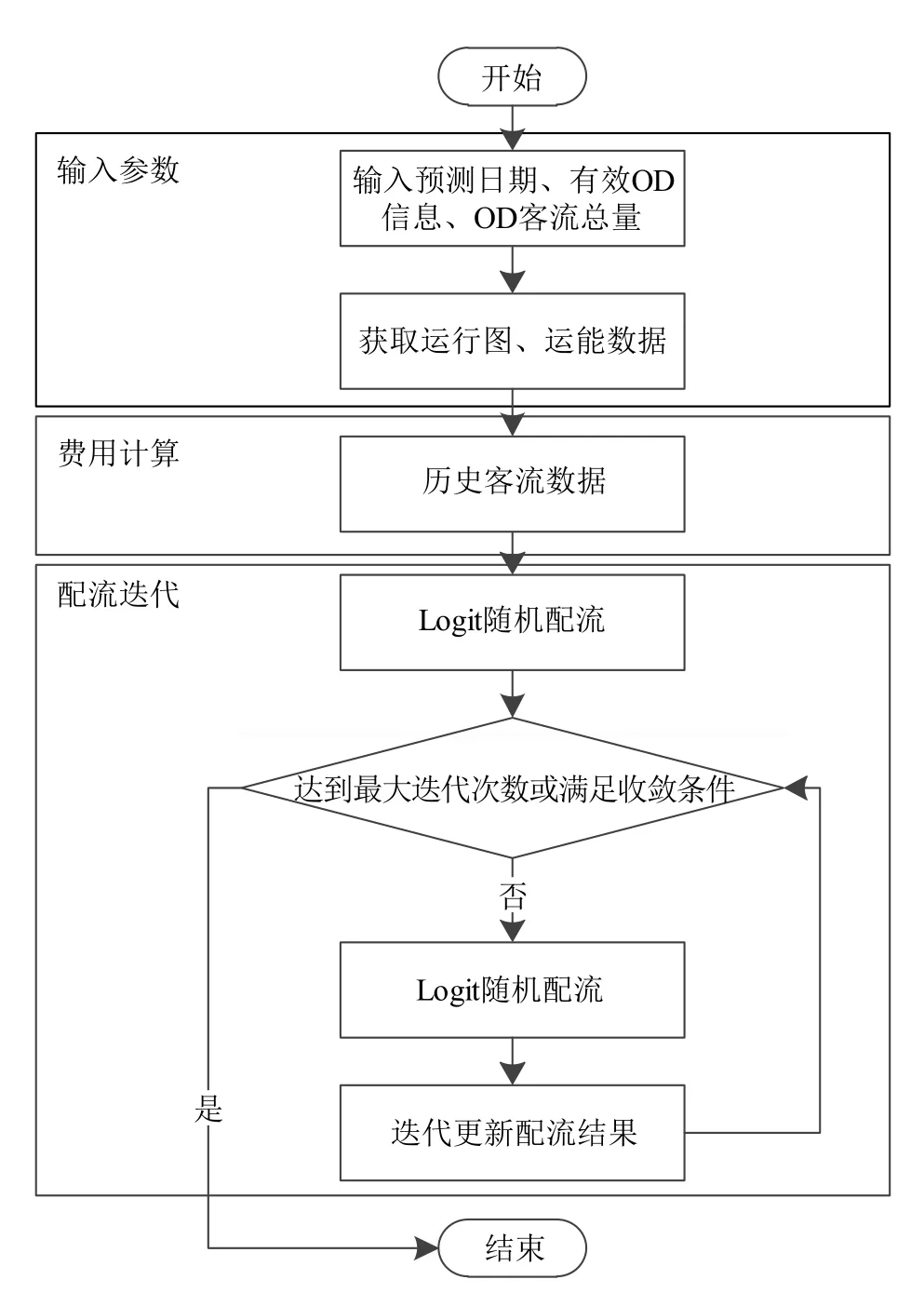
图6　配流计算流程示意图

3算例分析

以上海虹桥到北京南、上海虹桥到南京南的OD 客流为例，将旅客选择乘坐的不同车次视为 OD间的不同路径，根据 2014 年 3 月 15 日的数据进行计算，设置最大迭代次数为 20，收敛阈值为 0.02。

3.1上海虹桥到北京南客流分配

上海虹桥到北京南的客流分配结果如图7和图8所示，各车次所对应的广义出行费用如图 9 所示。结合各车次所分配的客流数量可以看出，旅客较为集中地分布于广义出行费用相对较少的车次上。

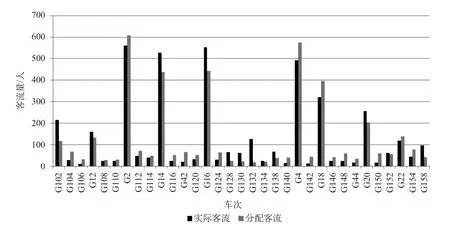
图7　上海虹桥到北京南各车次配流结果与实际值对比

图8　上海虹桥到北京南各时段配流结果与实际值对比

图9　上海虹桥到北京南各车次广义出行费用

上海虹桥到北京南配流迭代收敛偏差的变化情况如图 10 所示，可以看出在第 11 次迭代时收敛偏差小于收敛阈值，迭代停止。

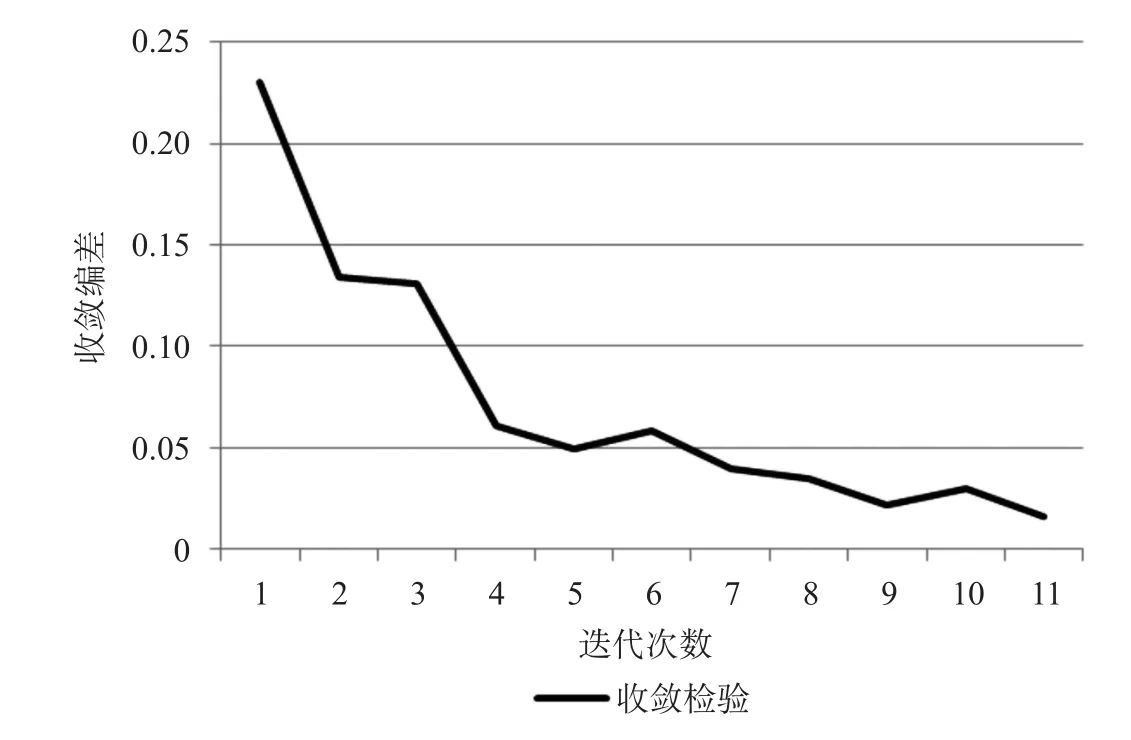
图10　上海虹桥到北京南配流迭代偏差收敛情况

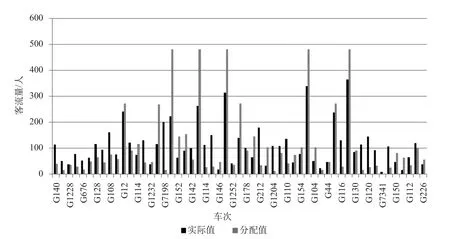
图11　上海虹桥到南京南各车次配流结果与实际值对比

从以上计算结果可以看出，上海虹桥到北京南的客流分配结果与实际客流分布较为吻合。

3.2上海虹桥到南京南客流分配

上海虹桥到南京南的客流分配结果如图11和图12所示。

图12　上海虹桥到南京南各时段配流结果与实际值对比

上海虹桥到南京南的配流结果中，部分车次(如 G18，G16，G14，G2，G4) 的分配值要显著大于实际值，部分车次 (如 G130，G12) 的分配结果较为准确。查询当天的票额分配结果如表3所示。

误差较大的车次长途票比例较大，短途票比例较小，反之配流结果误差较小的车次的短途票比例均大于长途票。由于上海虹桥到南京南属于短途票，模型求解过程中票额原始分配数据未知，因而拥挤费用函数所需的路径最大容量参数采用列车运行图数据，与实际分配的短途票额相差较大，从而造成误差；若能获取 OD 间更准确的票额预分数据作为最大载客量参数，可以得到更为准确的结果。

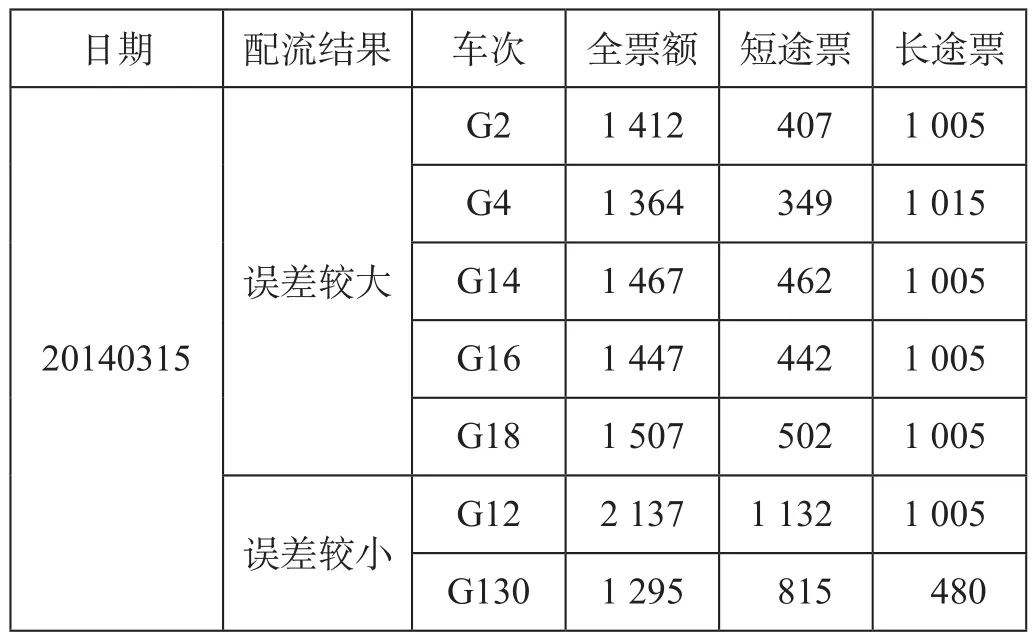
表3　部分车次票额分布情况 　张

4结束语

铁路客流分配相关理论研究是科学有效地解决客流预测问题，提高客运专线运输效率和铁路客运服务质量，从而提升铁路运输产品在运输市场上的竞争力的必要步骤与重要内容。铁路运输网络结构复杂，网络特性难以量化，旅客组成复杂，客运产品设计影响因素较多，因而客流分配问题应结合铁路运输自身特点进行研究。基于随机用户均衡理论构建的铁路客流分配模型及设计的模型求解算法，实现了在已知OD 客流预测总需求和列车运行图的情况下对 OD 客流进行分配。基于实际售票数据对模型进行了算例分析，验证了模型的有效性。目前的算法仍有改进的空间，通过调整算法中费用函数的参数及扩展费用函数覆盖范围，同时借助票额预分数据，可以更准确地反映旅客的路径选择行为。

[1] 赵 旭，庞京成. 网络化运营下的城市轨道交通客流时间分布特性分析[J]. 华东公路，2014(4)：124-126.

ZHAO Xu，PANG Jing-cheng. Analysis of City Rail Traffic Flow Time Distribution Network Operation[J]. East China Highway，2014(4)：124-126.

[2] 石小法，王 炜. 动态用户均衡配流模型的研究[J]. 系统工程理论与实践，2001，21(1)：130-133.

SHI Xiao-fa，WANG Wei. A Study on Dynamic User-Optimized Traffic Assignmen[J]. Systems Engineering—Theory & Practice，2001，21(1)：130-133.

[3] 况爱武，王正武，李炳林. 多用户类弹性需求随机用户均衡模型及其求解[J]. 长沙理工大学学报 (自然科学版)，2007，4(2)：16-20.

KUANG Ai-wu，WANG Zheng-wu，LI Bing-lin. Model and Its Solution for Stochastic User Equilibrium Traffic Assignment with Multiple User Classes and Variable Demand[J]. Journal Of Changsha University Of Science and Technology (Natural Science)，2007，4(2)：16-20.

[4] 刘新华. 基于时刻表的地铁动态配流模型研究[D]. 西安：长安大学，2013.

[5] 四兵锋，孙壮志，赵小梅. 基于随机用户平衡的混合交通网络流量分离模型[J]. 中国公路学报，2006，19(1)：93-98.

SI Bing-feng，SUN Zhuang-zhi，ZHAO Xiao-mei. Mixed Traffic Network Flow-Split Model based on Stochastic User Equilibrium[J]. China Journal of Highway and Transport，2006，19(1)：93-98.

[6] 冯 妍，李得伟. 基于 Logit 模型的城际运输通道客运量分担率计算研究[J]. 铁道运输与经济，2016，38(4)：47-51.

FENG Yan，LI De-wei. Research on Passenger Traffic Volume Sharing Rate of Inter-City Transport Corridor based on Logit Model[J]. Railway Transport and Economy，2016，38(4)：47-51.

[7] 孔繁钰. 网络化条件下轨道交通客流分布问题研究[D]. 上海：同济大学，2007.

[8] 邓军生，孔繁钰. MSA 算法求解轨道交通 SUE 模型问题研究[J]. 重庆科技学院学报 (自然科学版)，2008，10(1)：129-131.

DENG Jun-sheng，KONG Fan-yu. Study on Stochastic User Equilibrium Model and Algorithm for Rail Transition[J]. Journal of Chongqing University of Science and Technology (Natural Sciences Edition)，2008，10(1)：129-131.

责任编辑：刘 新

High-Speed Train Traffic Assignment Method based on Trip Time Slot

WENG Sheng-yuan, SHAN Xing-hua

(Institute of Computing Technology, China Academy of Railway Sciences, Beijing 100081，China)

Based on the analysis of high-speed train traffic distribution characteristics in different time slots and the relationship between traffic distribution and train service frequency, the paper defines the generalized passenger trip cost as the sum of trip time slot cost and congestion cost, and builds the user equilibrium assignment model for high-speed trains and gives the solving method of Logit random network loading algorithm combined with successive average methods. Finally, the validity of model is verified according to the method with OD traffic data between Shanghai Hongqiao Station and Beijing South Station and between Shanghai Hongqiao Station and Nanjing South Station.

Traffic Assignment; User Equilibrium Model; Logit Algorithm; Successive Average Method

1003-1421(2016)09-0006-09

U293.13

A

10.16668/j.cnki.issn.1003-1421.2016.09.02

2016-02-24

国家自然科学基金项目 (U1334207)