基于相关性分析的售票曲线相似度计算模型

王 浩，马敏书，房红征

（1.北京市高速交通工具智能诊断与健康管理重点实验室，北京100039；2.北京交通大学交通运输学院，北京100044）

基于相关性分析的售票曲线相似度计算模型

王 浩1，马敏书2，房红征1

（1.北京市高速交通工具智能诊断与健康管理重点实验室，北京100039；2.北京交通大学交通运输学院，北京100044）

售票曲线相似度作为铁路短期客流预测模型中的重要输入，决定预测结果的准确度。为了更合理地计算售票曲线相似度，在阐述售票曲线相似度概况的基础上，针对铁路短期客流预测的问题，提出简单计算模型、常用加权计算模型和基于相关性分析的计算模型，分别利用各模型计算得到的售票曲线相似度值对铁路短期客流进行预测。结果表明，基于相关性分析的计算模型的预测结果明显优于常用加权计算模型，即合理引入的相关性分析结果成分越多，预测效果越好。

相似度；相关系数；预测模型；售票数据

有效的铁路客流预测不但能够指导铁路资源的合理配置，而且能够提高铁路部门的收益[1-2]。铁路售票预测方法有很多。WICKHAM R R[3]提出改善的打包模型 (Advanced Pick Up)，通过有效利用已有的售票信息进行预测，提高预测精度；2003 年，WEATHERFORD L R 和 KIMES S E[4]提出一种通过计算订票曲线相似度来区分历史数据在预测中所起作用，进而对历史数据进行加权并预测的方法；2009 年，TSAI T H[5]提出三阶段法 (Three-Stage-Model)，并论证合理区分不同预售期的售票数据在计算相似度过程中的作用能够极大提高预测精度，但其区分依据是欧式距离，简单认为数据重要性大小只与应预测数据的时间距离远近有关。为更加准确地描述相对于同一发车时间不同提前时间的累计售票数据，以及不同历史数据对预测结果的影响，通过对上一年同期数据进行相关性分析 (计算线性相关系数)，用计算所得的相关系数来准确描述曲线相似度，可以有效区分不同数据在预测当中所起的作用，从而得到更加准确的预测结果。

1　售票曲线相似度计算模型

1.1售票曲线相似度

相似度计算通常通过已知数据的变化趋势来推算未知数据的应用，在铁路售票数据的预测中存在巨大应用潜力[6]。铁路在售票过程中不断积累历史数据，而历史数据与未来数据间有一定的相关关系，售票数据会呈现出一定的周期性变化，因而通过计算不同时间的售票曲线相似度，可以建立历史数据与未来数据的相似关系，实现对未来数据预测的有效指导。

假定有 n 个发车日的售票数据 (为方便分析，选择 n 为 1 周 7 天的倍数，即 n = 7m，m ∈ Z+)，Di表示第 i 个发车日，其中 di,0表示第 i 个发车日的最终累计售票量，di, j表示第 i 个发车日前 j 天的累计售票量，以此类推。在计算 Dx日数据曲线 (不含 dx,0) 与 Dy日数据曲线 (不含 dy,0）的相似度 Dx, y时(0≤x＜y≤n，并且 x，y ∈ Z+)，由于 dy,0为待预测数据，数据曲线不包含 dx,0，dy,0。Dx, y实际代表Dx日数据曲线 (不含 dx,0) 与 Dy日数据曲线 (不含 dy,0) 变化趋势的相似程度。

1.2现有曲线相似度计算模型

1.2.1简单计算模型

曲线相似度的简单计算模型是指计算由 2 组数据所绘成曲线的纯几何相似程度的模型[7]。纯几何相似程度没有考虑每个数据在计算中的不同作用，即默认为每个数据在计算相似度过程中所起的作用相同，虽然这种计算方法在一些预测问题中还会用到，但其容易使问题绝对化，不能区分不同数据对计算结果的影响，因而只适用于纯数据计算，不涉及解决实际问题。简单计算模型的计算公式为

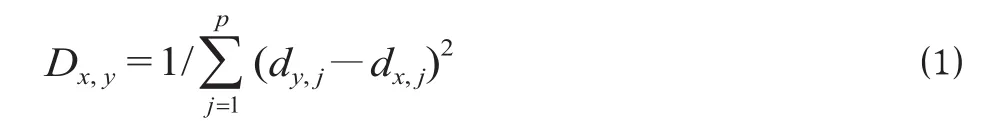
1.2.2常用加权计算模型

曲线相似度的加权计算模型是指计算由 2 组经过加权的数据所绘成曲线抽象相似程度的模型，是目前计算曲线相似度的常用方法。加权分为多种形式的加权，其目的是为了区分不同数据在计算曲线相似度时所起作用的大小。由于曲线上每个数据点赋予了不同的权重，所赋权值大的数据点在计算曲线相似度时所起的作用也大，因而不能只通过 2 条曲线的几何趋势即判断其相似程度。

在计算 Dx日数据曲线 (不含 dx,0) 与 Dy日数据曲线 (不含 dy,0) 的相似度时，计算结果用 Dx, y表示，将三阶段法中计算相似度的模型定义为 Model，则Model 的计算公式为

计算相似度是三阶段法中的第一步，TSAI T H经过相关论证，最终得出较为合理的预测模型，计算公式为

2　基于相关性分析的售票曲线相似度计算模型

2.1相关性分析方法

在实际预测当中会发现，用于预测的数据在预测当中所起的作用并非由欧氏距离简单区分[8]。为了能有效区别不同数据对预测结果的影响，可以通过对相关性的研究，进行以下 2 种形式的线性相关性分析，用以区分不同数据在预测中所起的作用，进而对公式 ⑵ 中 1/j2和 ( y－x) 这 2 项进行改进。这里分别用第一相关系数 cj和第二相关系数 c'k(均为线性相关系数) 来表示相关性分析结果，其定义如下。

（1）第一相关系数。为了区别不同提前天累计售票数据与发车日累计售票数据的相关性，用上年同期的数据进行相关性分析，定义第一相关系数 cj如下。

式中：cj为发车日累计售票数据列 (j = 0) 与发车日前 j 天 (j = 1，2，…，p) 累计售票数据的相关系数；di, j为第 i 个发车日前j 天的累计售票数据；。

（2）第二相关系数。为了区别不同发车日累计售票数据与要预测发车日累计售票数据的相关性，定义第二相关系数 c'k如下。将 di,0按周进行排列，则能分成 m 周，以第 1 列为例，分别求得周一与前一天 (k = 1)、前 2 天 (k = 2)、…、前 q 天 (k = q) 的相关系数 c'1，c'2，…，c'q。例如，c'1等于星期一这一列阴影部分与星期日一列阴影部分的相关系数，以此类推，如表1 所示。

表1　实验数据按照周进行排列

其中：

这样可求得星期一与前一天 (k = 1)、前 2 天(k = 2)、…、前 q 天 (k = q) 的线性相关系数 c'1，c'2，…，c'q。

2.2基于相关性分析的计算模型

改善模型当中的参数或因式，是对模型进行优化的一种常用方法，在引入 cj，c'k时有多种方法，根据实验比较，按下述方法引入可获得较为准确的预测结果。为区分开售时间段内不同日期累计售票量对预测结果的影响，把用欧式距离区分的因式改为引用相关系数区分的因式，即将 Model 中 j2一项改为 1/cj，把所得模型定义为 Model-1。则Model-1 计算公式为

为了进一步区分不同发车日累计售票量 (即历史数据) 对预测的影响，在 Model-1 的基础上又将欧氏距离区分因式 ( y－x) 改为引用相关系数分析区分因式，把所得模型定义为 Model-2。则Model-2 计算公式为

式中：k = y－x。

3　模型比较

3.1方法比较

现对公式 ⑵、⑹、⑺ 即 Model、Model-1、Model-2 这 3 个模型的预测效果进行对比。为减少数据波动性影响并简化预测过程，现规定只通过 1周之内的数据对发车日售票量进行预测。如表2 所示，以阴影部分为例，当预测第 i + 6 个发车日的数据 (这里真实数据是 di + 6, 0)，则只需要用到阴影部分(1 个测试集) 的数据进行预测，预测完 1 个数据，向下移动 1 行再对第 i + 7 个出发日的数据进行预测 (真实数据为 di + 7, 0) 进行预测，以此类推，这样可得到从 D7到 Dn共 n－6 个预测数据。

表2　用于预测的历史数据

为了验证新建模型的优越性，通过应用计算售票曲线相似度的预测方法，对所选实验数据进行预测，再比较预测结果的精确，从而反推模型优越性。这里选取车次为 G1，OD 为北京南到上海虹桥(终到站)，席别为二等座，时间段为 2014年10月7日—2015年3月1日共 147 天 (21 周) 的数据作为实验数据，基本涵盖各种情形的订票数据曲线，数据具有一定代表性。这里 n = 147，m = 21，根据上述实验数据的使用方法，即可获得测试集个数为 141个，从而得到 2014年10月13日—2015年3月1日共 141 天的预测数据。然后将所得预测值与对应的真实值进行比较。由于要预测年的部分数据未知，cj，的计算由上年同期数据计算所得，计算结果如图1和图2所示。

图1　cj计算结果

图2　计算结果

预测结果的计算公式为

这样可得到 2014年10月13日—2015年3月1日141 个发车日的预测数据 (2014年10月13日的数据是由 2014年10月7日—2015年10月12日数据预测所得，以此类推)。

3.2结果比较

通过计算预测结果的绝对相对误差 (MAPE) 来分析预测精度。

令 h = i + 6，则 MAPEh的计算公式为

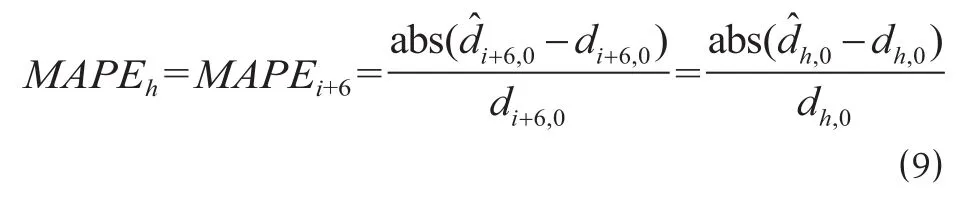
为了分析方便并提高误差分析的可靠性，选取 2014年10月14日—2015年3月1日的 140 天共 20 周预测误差值进行分析 (8≤h≤147)，对所得误差按星期求平均值，计算公式为

式中：w = 1 表示星期一；w = 2表示星期二；…；w = 7 表示星期日。

图3　计算结果

由图3可以看出，Model-1、Model-2 的预测结果明显优于 Model，而 Model-2 又明显优于Model-1。由此可知，合理引入相关性分析结果，相对于只单纯基于欧氏距离的相似度计算模型预测效果更好，而且合理引入的相关性分析结果成分越多，预测效果越好。

4　结束语

基于相关性分析的售票曲线相似度计算模型为预测提供了新思路，这种预测模型能够极大改善预测效果，相对于基于欧氏距离的相似度计算模型更加灵活，能够适应不同类型数据的预测。此外，基于相关性分析的售票曲线相似度计算方法能够发现数据间关联性，对于进一步研究其内在联系有一定指导作用。但是，该模型也存在一些不足，比如实验数据的选取和预测过程中数据的应用具有一定经验性，需要进一步完善。基于相关性分析的售票曲线相似度计算模型的适应性分析是下一步重点研究方向。

[1] 高 慧，赵建玉，贾 磊. 短时交通流预测方法综述[J].济南大学学报(自然科学版)，2008，22(1)：88-94.

GAO Hui，ZHAO Jian-yu，JIA Lei. Summary of Short-Time Traffic Flow Forecasting Methods[J]. Journal of University of Jinan(Science and Technology)，2008，22(1)：88-94.

[2] 宋嘉雯，瞿何舟. 基于客流性质的铁路客流预测方法[J].铁道运输与经济，2011，33(3)：87-90.

SONG Jia-wen，QU He-zhou. Forecast Method of Railway Passenger Flow based on the Passenger Flow Characrer[J]. Railway Transport and Economy，2011，33(3)：87-90.

[3] WICKHAM R R. Evaluation of Forecasting Techniques for Short-Term Demand of Air Transportation[R]. Cambridge：Flight Transportation Laboratory，1995.

[4] WEATHERFORD L R, KIMES S E. A Comparison of Forecasting Methods for Hotel Revenue Management[J]. International Journal of Forecasting，2003，19(3)：401-415.

[5] TSAI T H. A Temporal Case Retrieval Model to Predict Railway Passenger Arrivals[J]. Expert Systems with Applications，2009，36(5)：8876-8882.

[6] 贾俊芳，孙晚华，刘 华. 城际列车开行方案的客运量预测及评价[J]. 北京交通大学学报 (自然科学版)，2004，28(6)：95-98.

JIA Jun-fang，SUN Wan-hua，LIU Hua. Traffic Volume Forecast and Evaluation of Intercity Passenger Train Operation[J]. Journal of Beijing Jiaotong University，2004，28(6)：95-98.

[7] 孙晚华，刘 刚. 铁路城际客流预测模型的研究[J]. 北京交通大学学报 (自然科学版)，2005，29(3)：84-87.

SUN Wan-hua，LIU Gang. Research on the Model of Forecasting Passenger Flow of the Intercity Train[J]. Journal of Beijing Jiaotong University，2005，29(3)：84-87.

[8] 王 达，荣 冈. 时间序列的模式距离[J]. 浙江大学学报(工学版)，2004，38(7)：795-798.

WANG Da，RONG Gang. Pattern Distance of Time Series[J]. Journal of Zhejiang University(Engineering Science)，2004，38(7)：795-798.

责任编辑：吴文娟

The Similarity Calculating Model of Ticket Sales Curve based on Correlation Analysis

WANG Hao1，MA Min-shu2，FANG Hong-zheng3

(1.High-Speed Transport Intelligent Diagnostics and Health Management—The Key Laboratory of Beijing Municipality, Beijing 100039, China; 2.School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China)

The similarity of the ticket sales curve is an important input in the short-term passenger flow forecasting model, which determines the accuracy of forecasting results. In order to calculate the similarity of the sales curve more reasonably, a simple calculation model, a weighted calculation model and a relational analysis-based calculation model are put forward on the basis of describing the similarity of the selling curve and the short-term passenger flow forecasting, and the short-term passenger flow is forecasted by using the similarity value calculated by the model. The result shows that the prediction model based on the correlation analysis is better than the commonly used weighted calculation model, that is, the more the correlative analysis results are, the better the prediction result will be.

Similarity; Correlation Coefficient; Prediction Model; Ticketing Data

1003-1421(2016)11-0072-05

U293.13

A

10.16668/j.cnki.issn.1003-1421.2016.11.15

2016-02-10

2016-08-02

中国铁路总公司科技研究开发计划课题(2013F019)