从“两点之间,线段最短”分析
吴子兵
所谓的变式教学,就是对初中数学中的问题从不同角度、不同情境、不同背景以及不同层次进行变式,进而揭示出问题的本质,寻找不同知识之间的联系的一种教学方法,目前已经在初中数学教学中得到了非常广泛的应用.通过变式教学的应用,不仅能够培养学生的思维创新能力和探索能力,还能让学生在不断的变式训练中感受到知识的变化,从而对知识有一个深刻的理解.基于此,本文以“两点之间,线段最短”的相关知识为例,重点研究了变式教学在初中数学教学中的应用.
在近几年的中考中,“两点之间,线段最短”方面的知识占据了一定的比例,而且题型始终在变化,但是,这些题基本都是由课本上原题变型得到的.某学校的教师在进行苏教版初中数学七年级《平面图形的认识》中的“两点之间,线段最短”的教学时,对变式教学在初中数学中的应用进行了探究.
教师在上课时对线段、直线以及射线等进行了复习,随后通过一个案例引出了“两点之间,线段最短”的教学:同学们,小红和小明是非常好的朋友,他们住在一条小河的两边,一天小红要去找小明玩,她有两条路可以走,一条路是走小河上面的小桥,一条路是绕过小河,走旁边的柏油路,你们知道这两种走法哪个更近一些么?这时同学们都争先恐后的发言,有的人认为走小桥近,而有的人却认为走旁边的柏油路近,这时教师可以引入“两点之间,线段最短”的教学,在黑板上画出一定的图形,让学生自己领悟.学生一看教师画出来的图形,顿时明白“啊,原来走小桥这么近啊.”
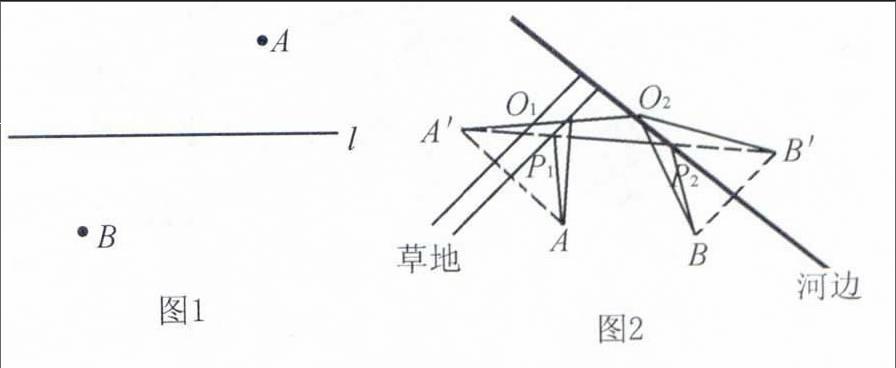
在学习完“两点之间,线段最短”的相关内容之后,教师还可以利用该内容带领学生分析一下变式教学,如教师可以给学生出一道题“同学们,我们可以看见在图中(图1)煤气管道的两侧有两个村庄,一个是A,一个是B,煤气单位要在煤气管道l上修建一个煤气站,同时供两个村庄使用,那么煤气站应该修建在什么地方所使用的输气管线才会最短?”通过本节课的学习,学生会很快地说出“将A、B两点连接起来,该线与煤气管道的交点就是煤气站应该修建的位置.”这样也使“两点之间,线段最短”的说法得到了验证.
之后教师对该题进行一下变式,“如果我将A、B的位置由l的两侧变成同侧,施工人员仍然要在河边
l上修建一个水站,同时为A、B村庄供水,水站应该修建在什么地方所用的输送管道最短.”这只是对上述的题进行了一下变型,有的同学可能会感觉到茫然,教师可以对学生进行引导“你们看,这道题和上面的题是不是很类似,但是又不一样?”学生们会频频点头,“那么你们只要按照上一道题的思路,就能将该题解决,老师相信你们.”这时有个学生说“老师,是不是只要
作点A关于l的对称点A′,再连接A′B,与l的交点就是水站的修建点?”听了学生的话后教师非常惊讶,对他竖起了大拇指“回答的非常正确.”之后教师可以详细地为学生讲一下其中的原理,使学生对“两点之间,线段最短”的理念有一个更加深刻的认识.
随后,教师又进行了一个变型,点数不需要改变,可以将线数变一下,也就是说有两个点,两条线,这也是“两点之间,线段最短”的一种变型.“同学们,现在图2中的A点为马圈,B点为帐篷,一天牧马人将马从A点牵出,先到草地喂了一会马,又到河边饮马,最后回到帐篷B,你们觉得牧马人应该怎样走,他这一天的路线才会最短?”有了上一个变式之后,学生已经有了一定的思考能力,有的学生迅速看出了其中的区别:这道题与上述的水
站问题相比较,多出了一条线,但是同样是“两点之间,线段最短”的相关问题,可以过A、B作关于草地和河边的对称点,分别为A′、B′,连接A′B′,分别交草地、河边于P1、P2,连接P1A、P2B,之后在“两点之间,线段最短”的基础上求出三边的最短值,这就是牧马人一天走的最短路线.教师不禁对该学生的思维由衷赞叹,由此可见,学生已经完全掌握了“两点之间,线段最短”问题,而且不管怎样变型都能非常容易地进行解决.
综上所述,在进行初中数学的教学时,一定要能够对原题进行延伸和扩展,从而培养学生举一反三的能力以及思维创新的能力.可以在情境改变、角度改变以及背景改变的基础上,对同一种类型的题进行归纳总结,让学生按照不同的条件进行问题的解析,进而使学生养成推理、探索的能力.由此可见,变式教学在初中数学的教学中具有非常重要的意义,尤其是在关于“两点之间,线段最短”知识方面,更能发挥出变式教学的作用,使学生养成举一反三的能力,提高学生的学习能力.

